K-means聚类算法详细介绍
目录
🍉简介
🍈K-means聚类模型详解
🍈K-means聚类的基本原理
🍈K-means聚类的算法步骤
🍈K-means聚类的优缺点
🍍优点
🍍缺点
🍈K-means聚类的应用场景
🍈K-means的改进和变体
🍉K-means聚类算法示例
🍈问题
🍍数据准备
🍍选择K值
🍍运行K-means聚类
🍍分析聚类结果
🍈完整代码实现
🍈代码解释
🍉简介
🍈K-means聚类模型详解
- K-means聚类是一种常见且高效的无监督学习算法,用于将数据集分成K个簇(clusters)。本文将详细介绍K-means聚类的基本原理、算法步骤、优缺点以及应用场景。
🍈K-means聚类的基本原理
- K-means聚类通过最小化样本到其所属簇中心的距离来实现数据的分组。具体而言,K-means的目标是将数据分成K个簇,并使每个簇中的数据点到其质心(centroid)的欧氏距离平方和最小。
假设我们有一个数据集${x_1, x_2, \ldots, x_n}$,其中每个数据点$x_i$是一个d维向量。我们需要将这些数据点分成K个簇${C_1, C_2, \ldots, C_K}$。K-means的优化目标可以表示为:
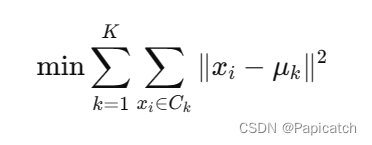
其中,$\mu_k$表示簇$C_k$的质心。
🍈K-means聚类的算法步骤
K-means聚类算法主要包括以下步骤:
- 初始化:随机选择K个数据点作为初始质心。
- 分配簇:对于数据集中的每个数据点,计算其到各个质心的距离,并将其分配到距离最近的质心所在的簇。
- 更新质心:对于每个簇,计算所有分配到该簇的数据点的平均值,更新该簇的质心。
- 重复:重复步骤2和3,直到质心不再发生显著变化,或者达到预设的迭代次数。
🍈K-means聚类的优缺点
🍍优点
- 简单易实现:K-means算法简单且容易理解和实现。
- 高效:时间复杂度为$O(n \cdot K \cdot t)$,其中n是数据点数量,K是簇的数量,t是迭代次数。
- 适用广泛:适用于很多实际问题,如图像分割、文档聚类等。
🍍缺点
- 需要预设K值:必须提前确定簇的数量K,且K值的选择对结果影响较大。
- 对初始质心敏感:初始质心的选择会影响最终结果,可能会陷入局部最优。
- 对噪声和异常值敏感:噪声和异常值可能会严重影响簇的结果。
🍈K-means聚类的应用场景
K-means聚类在实际中有广泛的应用,包括但不限于:
- 图像处理:如图像分割、颜色量化等。
- 市场营销:客户分群,根据消费行为将客户分成不同的群体。
- 文本处理:文档聚类,将相似的文档分在一起。
- 生物信息学:基因表达数据分析,将具有相似表达模式的基因分在一起。
🍈K-means的改进和变体
为了克服K-means的一些缺点,研究人员提出了许多改进和变体方法:
- K-means++:通过改进质心初始化过程,减少算法陷入局部最优的可能性。
- Mini-batch K-means:使用小批量数据进行训练,适用于大规模数据集。
- 谱聚类:结合图论和K-means,适用于非凸形状的簇。
🍉K-means聚类算法示例
- 为了更好地理解K-means聚类算法在现实生活中的应用,我们将以一个具体的示例来演示其使用过程和效果。我们将使用K-means聚类算法对客户进行分群,以帮助企业进行市场营销策略的制定。
🍈问题
假设我们是一家电子商务公司,希望通过分析客户的购买行为,将客户分成不同的群体,以便进行有针对性的市场营销。我们拥有以下客户数据集:
- 客户ID
- 年龄
- 年收入(以美元计)
- 年消费额(以美元计)
🍍数据准备
首先,我们需要对数据进行预处理和标准化,因为不同特征的量纲可能会影响聚类效果。
import pandas as pd
from sklearn.preprocessing import StandardScaler# 创建示例数据集
data = {'CustomerID': [1, 2, 3, 4, 5],'Age': [25, 34, 45, 23, 35],'Annual Income (k$)': [15, 20, 35, 60, 45],'Spending Score (1-100)': [39, 81, 6, 77, 40]
}
df = pd.DataFrame(data)# 标准化特征
scaler = StandardScaler()
df[['Age', 'Annual Income (k$)', 'Spending Score (1-100)']] = scaler.fit_transform(df[['Age', 'Annual Income (k$)', 'Spending Score (1-100)']])
🍍选择K值
通常情况下,选择K值可以通过“肘部法则”来确定。我们绘制不同K值下的SSE(误差平方和)曲线,选择拐点作为K值。
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt# 计算不同K值下的SSE
sse = []
for k in range(1, 11):kmeans = KMeans(n_clusters=k, random_state=0)kmeans.fit(df[['Age', 'Annual Income (k$)', 'Spending Score (1-100)']])sse.append(kmeans.inertia_)# 绘制肘部法则图
plt.figure(figsize=(8, 5))
plt.plot(range(1, 11), sse, marker='o')
plt.title('Elbow Method for Optimal K')
plt.xlabel('Number of clusters')
plt.ylabel('SSE')
plt.show()
假设通过肘部法则确定K值为3。
🍍运行K-means聚类
使用K-means算法对客户进行分群。
# 运行K-means聚类
kmeans = KMeans(n_clusters=3, random_state=0)
df['Cluster'] = kmeans.fit_predict(df[['Age', 'Annual Income (k$)', 'Spending Score (1-100)']])# 查看聚类结果
print(df)
🍍分析聚类结果
通过可视化和统计分析,我们可以更好地理解每个簇的特征。
# 可视化聚类结果
plt.figure(figsize=(8, 5))
plt.scatter(df['Annual Income (k$)'], df['Spending Score (1-100)'], c=df['Cluster'], cmap='viridis')
plt.scatter(kmeans.cluster_centers_[:, 1], kmeans.cluster_centers_[:, 2], s=300, c='red')
plt.title('Customer Segments')
plt.xlabel('Annual Income (k$)')
plt.ylabel('Spending Score (1-100)')
plt.show()
此外,我们可以查看每个簇的中心和簇内数据点的分布情况:
# 查看每个簇的中心
centroids = kmeans.cluster_centers_
print("Cluster Centers:\n", centroids)# 查看每个簇的样本数量
print(df['Cluster'].value_counts())
🍈完整代码实现
import pandas as pd
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt# 创建示例数据集
data = {'CustomerID': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10],'Age': [25, 34, 45, 23, 35, 64, 24, 29, 33, 55],'Annual Income (k$)': [15, 20, 35, 60, 45, 70, 18, 24, 50, 40],'Spending Score (1-100)': [39, 81, 6, 77, 40, 80, 20, 60, 54, 50]
}
df = pd.DataFrame(data)# 标准化特征
scaler = StandardScaler()
df[['Age', 'Annual Income (k$)', 'Spending Score (1-100)']] = scaler.fit_transform(df[['Age', 'Annual Income (k$)', 'Spending Score (1-100)']])# 计算不同K值下的SSE
sse = []
for k in range(1, 11):kmeans = KMeans(n_clusters=k, random_state=0)kmeans.fit(df[['Age', 'Annual Income (k$)', 'Spending Score (1-100)']])sse.append(kmeans.inertia_)# 绘制肘部法则图
plt.figure(figsize=(8, 5))
plt.plot(range(1, 11), sse, marker='o')
plt.title('Elbow Method for Optimal K')
plt.xlabel('Number of clusters')
plt.ylabel('SSE')
plt.show()# 根据肘部法则选择K值为3
k = 3# 运行K-means聚类
kmeans = KMeans(n_clusters=k, random_state=0)
df['Cluster'] = kmeans.fit_predict(df[['Age', 'Annual Income (k$)', 'Spending Score (1-100)']])# 查看聚类结果
print(df)# 可视化聚类结果
plt.figure(figsize=(8, 5))
plt.scatter(df['Annual Income (k$)'], df['Spending Score (1-100)'], c=df['Cluster'], cmap='viridis')
plt.scatter(kmeans.cluster_centers_[:, 1], kmeans.cluster_centers_[:, 2], s=300, c='red', marker='x')
plt.title('Customer Segments')
plt.xlabel('Annual Income (k$)')
plt.ylabel('Spending Score (1-100)')
plt.show()# 查看每个簇的中心
centroids = kmeans.cluster_centers_
print("Cluster Centers:\n", centroids)# 查看每个簇的样本数量
print(df['Cluster'].value_counts())
🍈代码解释
🍍导入必要的库:
pandas用于数据处理。numpy用于数值计算。StandardScaler用于标准化数据。KMeans用于K-means聚类。matplotlib用于数据可视化。
🍍创建示例数据集:
- 包含客户ID、年龄、年收入和消费评分。
🍍标准化特征:
- 使用
StandardScaler将特征缩放到相同的尺度,以提高聚类效果。
🍍选择K值:
- 使用肘部法则,通过计算不同K值下的SSE(误差平方和)来确定最佳K值。
- 绘制SSE随K值变化的曲线,选择拐点作为最佳K值。
🍍运行K-means聚类:
- 使用确定的K值运行K-means算法,对客户进行分群。
- 将分群结果添加到数据集中。
🍍可视化聚类结果:
- 绘制聚类结果的散点图,使用不同颜色表示不同的簇,并标出每个簇的质心。
🍍查看聚类结果:
- 打印每个簇的中心坐标和每个簇的样本数量,以更好地理解每个簇的特征。
希望这些能对刚学习算法的同学们提供些帮助哦!!!

相关文章:

K-means聚类算法详细介绍
目录 🍉简介 🍈K-means聚类模型详解 🍈K-means聚类的基本原理 🍈K-means聚类的算法步骤 🍈K-means聚类的优缺点 🍍优点 🍍缺点 🍈K-means聚类的应用场景 🍈K-mea…...
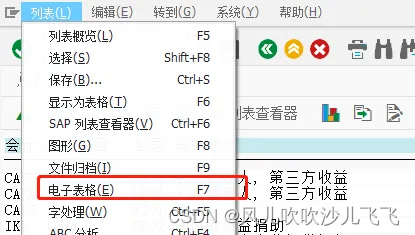
SAP FS00如何导出会计总账科目表
输入T-code : S_ALR_87012333 根据‘FS00’中找到的总账科目,进行筛选执行 点击左上角的列表菜单,选择‘电子表格’导出即可...

ROS参数服务器
一、介绍 参数服务器是用于存储和检索参数的分布式多机器人配置系统,它允许节点动态地获取参数值。 在ROS中,参数服务器是一种用于存储和检索参数的分布式多机器人配置系统。它允许节点动态地获取参数值,并提供了一种方便的方式来管理和共享配…...

QCC---DFU升级变更设备名和地址
QCC---DFU升级变更设备名和地址 这个很多人碰到这个疑问,升级了改不了设备名和地址 /******************************************************************************* Copyright (c) 2018 Qualcomm Technologies International, Ltd. FILE NAME sink_dfu_ps.c DESCRIPT…...

[力扣题解] 695. 岛屿的最大面积
题目:695. 岛屿的最大面积 思路 代码 深度优先搜索 // 深度搜索 class Solution { private:int area_max 0;int dir[4][2] {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};void dfs(vector<vector<int>>& grid, vector<vector<bool>>& …...

AI模型发展路径探析:开源与闭源,何者更胜一筹?
AI模型发展路径探析:开源与闭源,何者更胜一筹? 在当今快速发展的人工智能领域,AI模型成为推动技术创新和应用落地的关键。而评价一个AI模型“好不好”“有没有发展”,往往会引向一个重要话题:开源与闭源这…...

concurrency 并行编程
Goroutine go语言的魅力所在,高并发。 线程是操作系统调度的一种执行路径,用于在处理器执行我们在函数中编写的代码。一个进程从一个线程开始,即主线程,当该线程终止时,进程终止。这是因为主线程是应用程序的原点。然后…...

JavaScript如何让一个按钮的点击事件在完成之前禁用
在JavaScript中,要禁用一个按钮的点击事件直到某个操作完成,你可以将其点击事件用匿名函数的方式书写。 你可以将其在点击函数内设置为null来禁用按钮。 <button id"butto_n">点击抽奖</button><script>butto_n.onclick bu…...

透视App投放效果,Xinstall助力精准分析,让每一分投入都物超所值!
在移动互联网时代,App的推广与投放成为了每一个开发者和广告主必须面对的问题。然而,如何精准地掌握投放效果,让每一分投入都物超所值,却是一个令人头疼的难题。今天,我们就来谈谈如何通过Xinstall这个专业的App全渠道…...

【Linux杂货铺】进程通信
目录 🌈 前言🌈 📁 通信概念 📁 通信发展阶段 📁 通信方式 📁 管道(匿名管道) 📂 接口 编辑📂 使用fork来共享通道 📂 管道读写规则 &…...
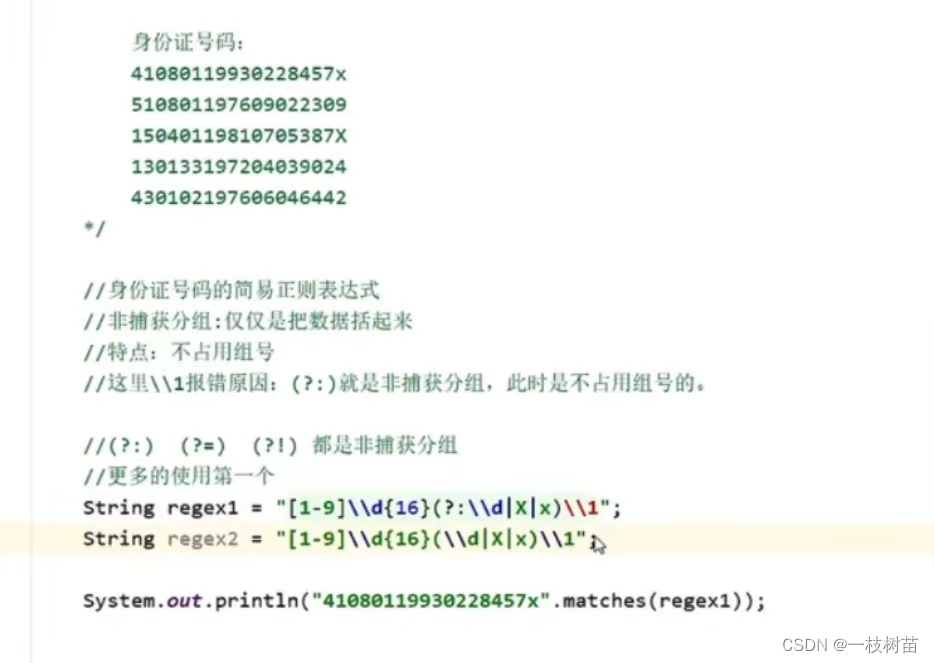
常用API(正则表达式、爬取、捕获分组和非捕获分组 )
1、正则表达式 练习——先爽一下正则表达式 正则表达式可以校验字符串是否满足一定的规则,并用来校验数据格式的合法性。 需求:假如现在要求校验一个qq号码是否正确。 规则:6位及20位之内,0不能在开头,必须全部是数字…...
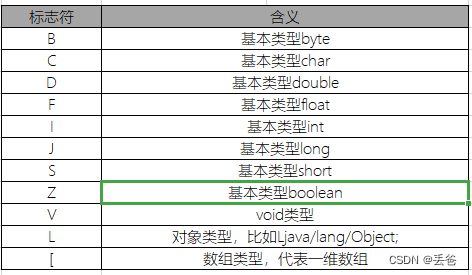
JVM学习-Class文件结构②
访问标识(access_flag) 在常量池后,紧跟着访问标记,标记使用两个字节表示,用于识别一些类或接口层次的访问信息,包括这个Class是类还是接口,是否定义为public类型,是否定义为abstract类型,如果…...

数据库连接项目
MySQL...

MySQL--InnoDB体系结构
目录 一、物理存储结构 二、表空间 1.数据表空间介绍 2.数据表空间迁移 3.共享表空间 4.临时表空间 5.undo表空间 三、InnoDB内存结构 1.innodb_buffer_pool 2.innodb_log_buffer 四、InnoDB 8.0结构图例 五、InnoDB重要参数 1.redo log刷新磁盘策略 2.刷盘方式&…...

ffplay 使用文档介绍
ffplay ffplay 是一个简单的媒体播放器,它是 FFmpeg 项目的一部分。FFmpeg 是一个广泛使用的多媒体框架,能够解码、编码、转码、复用、解复用、流化、过滤和播放几乎所有类型的媒体文件。 ffplay 主要用于测试和调试,因为它提供了一个命令行界面,可以方便地查看媒体文件的…...
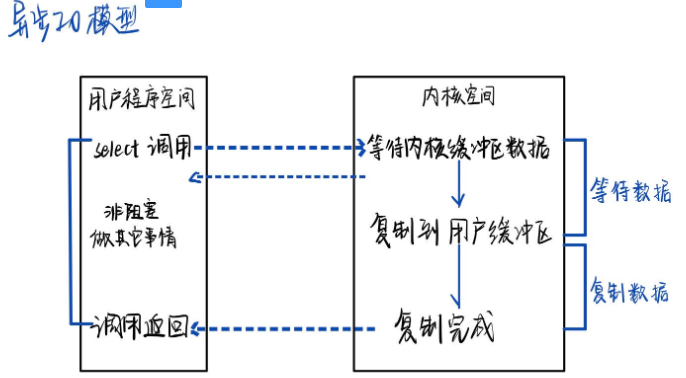
四种网络IO模型
📝个人主页:五敷有你 🔥系列专栏:面经 ⛺️稳中求进,晒太阳 IO的定义 IO是计算机内存与外部设备之间拷贝数据的过程。CPU访问内存的速度远高于外部设备。因此CPU是先把外部设备的数据读取到内存,在…...
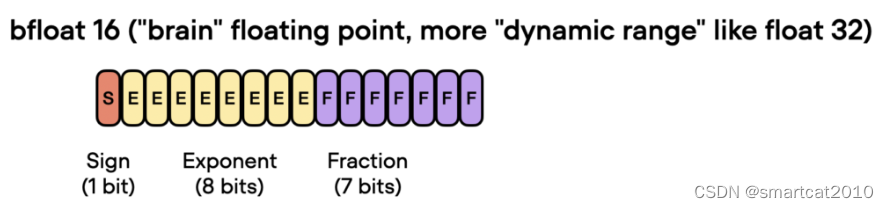
Mixed-precision计算原理(FP32+FP16)
原文: https://lightning.ai/pages/community/tutorial/accelerating-large-language-models-with-mixed-precision-techniques/ This approach allows for efficient training while maintaining the accuracy and stability of the neural network. In more det…...
的并发数量)
Go 控制协程(goroutine)的并发数量
在使用协程并发处理某些任务时, 其并发数量往往因为各种因素的限制不能无限的增大. 例如网络请求、数据库查询等等。 从运行效率角度考虑,在相关服务可以负载的前提下(限制最大并发数),尽可能高的并发。 在Go语言中,…...
:web渗透测试之CSRF跨站请求伪造)
web安全渗透测试十大常规项(一):web渗透测试之CSRF跨站请求伪造
渗透测试之CSRF跨站请求伪造 CSRF跨站请求伪造 CSRF跨站请求伪造...

YOLOv10尝鲜测试五分钟极简配置
最近清华大学团队又推出YOLOv10,真是好家伙了。 安装: pip install supervision githttps://github.com/THU-MIG/yolov10.git下载权重:https://github.com/THU-MIG/yolov10/releases/download/v1.0/yolov10n.pt 预测: from ult…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...


