代码随想录-Day20
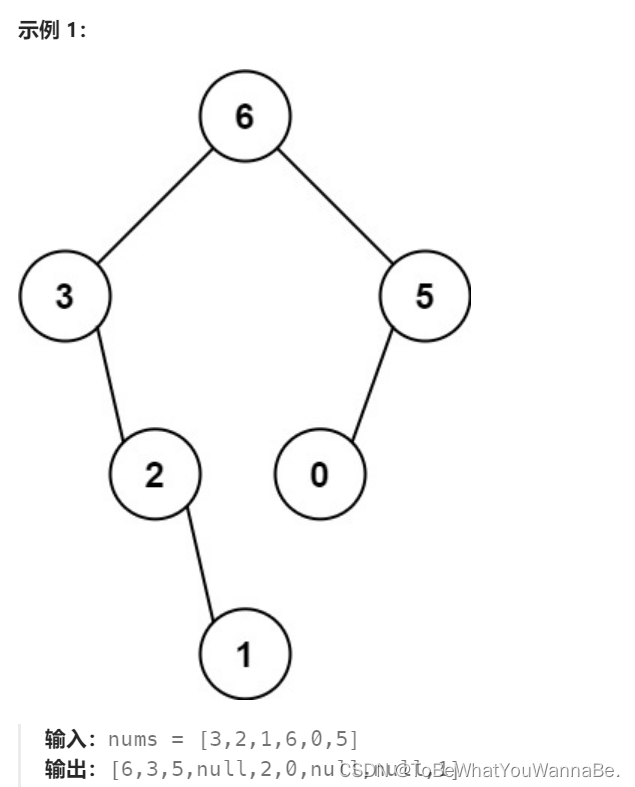
654. 最大二叉树
给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
创建一个根节点,其值为 nums 中的最大值。
递归地在最大值 左边 的 子数组前缀上 构建左子树。
递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 最大二叉树 。
方法一:递归
class Solution {public TreeNode constructMaximumBinaryTree(int[] nums) {return construct(nums, 0, nums.length - 1);}public TreeNode construct(int[] nums, int left, int right) {if (left > right) {return null;}int best = left;for (int i = left + 1; i <= right; ++i) {if (nums[i] > nums[best]) {best = i;}}TreeNode node = new TreeNode(nums[best]);node.left = construct(nums, left, best - 1);node.right = construct(nums, best + 1, right);return node;}
}
这段代码定义了一个名为 Solution 的类,其中有两个方法用于构建一棵最大二叉树。最大二叉树的定义是:树中的每个节点都是对应输入数组中从该节点所在位置开始往后的子数组中的最大值。以下是代码的详细解释:
-
public TreeNode constructMaximumBinaryTree(int[] nums)是主要接口,接收一个整型数组nums,并返回根据该数组构建的最大二叉树的根节点。它通过调用重载的construct方法来实现这个功能,初始化传入整个数组的起始下标0和结束下标nums.length - 1。 -
public TreeNode construct(int[] nums, int left, int right)是一个递归方法,用于根据输入数组nums从索引left到right的子数组构建最大二叉树。- 首先,检查边界条件,如果
left > right,表示当前子数组为空,没有节点可构建,返回null。 - 然后,在
left到right的范围内找到最大值的索引best。初始化时假设best为left,通过遍历该范围内的元素,如果发现更大的值,则更新best。 - 创建一个新的
TreeNode,其值为nums[best],即当前子数组中的最大值。 - 递归调用
construct方法构建左子树,参数为left和best - 1,意在构建以当前最大值左侧子数组为基础的最大二叉树。 - 同样递归调用构建右子树,参数为
best + 1和right,构建以当前最大值右侧子数组为基础的最大二叉树。 - 最后,返回当前节点,完成以
nums[best]为根节点的子树构建。
- 首先,检查边界条件,如果
通过这样的递归过程,代码能够高效地遍历整个数组,构建出整棵最大二叉树。这种方法充分利用了分治思想,每次递归调用都确保了以当前区间的最大值为根节点,从而保证了构建出的二叉树满足题目要求。
方法二:单调栈
class Solution {public TreeNode constructMaximumBinaryTree(int[] nums) {int n = nums.length;Deque<Integer> stack = new ArrayDeque<Integer>();int[] left = new int[n];int[] right = new int[n];Arrays.fill(left, -1);Arrays.fill(right, -1);TreeNode[] tree = new TreeNode[n];for (int i = 0; i < n; ++i) {tree[i] = new TreeNode(nums[i]);while (!stack.isEmpty() && nums[i] > nums[stack.peek()]) {right[stack.pop()] = i;}if (!stack.isEmpty()) {left[i] = stack.peek();}stack.push(i);}TreeNode root = null;for (int i = 0; i < n; ++i) {if (left[i] == -1 && right[i] == -1) {root = tree[i];} else if (right[i] == -1 || (left[i] != -1 && nums[left[i]] < nums[right[i]])) {tree[left[i]].right = tree[i];} else {tree[right[i]].left = tree[i];}}return root;}
}
这段代码实现了一个名为 Solution 的类,其中的 constructMaximumBinaryTree 方法接收一个整型数组 nums,并根据这个数组构建一棵最大二叉树。最大二叉树的特性是每个节点都是其子树(包括该节点)中最大值的节点。与之前递归的解法不同,这段代码采用了单调栈和两次遍历的方法来构造这棵树。
代码逻辑步骤如下:
-
初始化变量和数据结构:
n为数组nums的长度。stack是一个单调递减的整数栈,用于存放数组下标,保证栈顶元素对应的nums值是栈中已处理元素中的最大值。left和right数组分别记录每个元素在最大二叉树中的左孩子和右孩子的索引,初始化为-1。tree数组用于存储根据nums创建的TreeNode对象。
-
第一次遍历:
- 遍历
nums数组,创建每个节点并压入栈中。同时,根据栈的状态更新每个节点的左右孩子索引(在left和right数组中记录)。 - 当遇到一个比栈顶元素值更大的数时,说明栈顶元素右边的节点已经找到,更新相应索引,并将栈顶元素出栈,直到栈为空或遇到比当前元素小的值。这保证了栈中元素按照最大二叉树的右边界逆序排列。
- 遍历
-
构建最大二叉树:
- 根据
left和right数组以及栈中元素的关系,第二次遍历数组,为每个节点分配左右子树。这里通过判断条件确定当前节点应作为其父节点的左子树还是右子树,最后找到根节点(其左右孩子索引均为-1)。
- 根据
-
返回根节点:构建完成后,返回
root,即整个最大二叉树的根节点。
这种方法避免了递归调用,利用栈和两次遍历数组的方式,实现了从给定数组直接构建最大二叉树的功能,时间复杂度为 O(n),空间复杂度也为 O(n)。
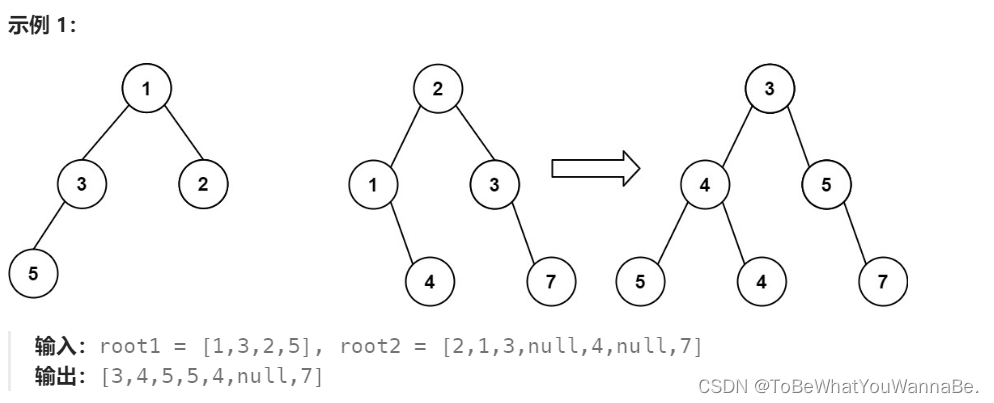
617. 合并二叉树
方法一:深度优先搜索
class Solution {public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {if (t1 == null) {return t2;}if (t2 == null) {return t1;}TreeNode merged = new TreeNode(t1.val + t2.val);merged.left = mergeTrees(t1.left, t2.left);merged.right = mergeTrees(t1.right, t2.right);return merged;}
}
这段代码定义了一个名为 Solution 的类,其中包含一个方法 mergeTrees,用于合并两棵二叉树 t1 和 t2。合并规则是:如果两个节点重叠,那么它们的值相加作为新节点的值;非空节点与空节点相遇时,非空节点将被保留。该方法递归地实现了这一过程,具体步骤如下:
-
基本情况检查:
- 首先,如果
t1为空,直接返回t2,表示当前子树以t2为准。 - 如果
t2为空,直接返回t1,表示当前子树以t1为准。
- 首先,如果
-
创建合并节点:
- 如果两个节点都不为空,创建一个新的
TreeNode,其值为t1.val + t2.val,这表示合并了两个节点的值。
- 如果两个节点都不为空,创建一个新的
-
递归合并子树:
- 对于新节点的左子树,递归调用
mergeTrees(t1.left, t2.left),将t1和t2的左子树合并,并将结果赋给新节点的左子指针。 - 对于新节点的右子树,递归调用
mergeTrees(t1.right, t2.right),将t1和t2的右子树合并,并将结果赋给新节点的右子指针。
- 对于新节点的左子树,递归调用
-
返回合并后的节点:
- 最终,返回新创建的合并节点,这样就完成了从当前节点开始的整个子树的合并。
通过这样的递归处理,整棵树被自顶向下地合并,直至所有节点都被正确处理,最终返回合并后树的根节点。这种方法简洁而高效,适合解决这类二叉树合并的问题。
方法二:广度优先搜索
class Solution {public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {if (t1 == null) {return t2;}if (t2 == null) {return t1;}TreeNode merged = new TreeNode(t1.val + t2.val);Queue<TreeNode> queue = new LinkedList<TreeNode>();Queue<TreeNode> queue1 = new LinkedList<TreeNode>();Queue<TreeNode> queue2 = new LinkedList<TreeNode>();queue.offer(merged);queue1.offer(t1);queue2.offer(t2);while (!queue1.isEmpty() && !queue2.isEmpty()) {TreeNode node = queue.poll(), node1 = queue1.poll(), node2 = queue2.poll();TreeNode left1 = node1.left, left2 = node2.left, right1 = node1.right, right2 = node2.right;if (left1 != null || left2 != null) {if (left1 != null && left2 != null) {TreeNode left = new TreeNode(left1.val + left2.val);node.left = left;queue.offer(left);queue1.offer(left1);queue2.offer(left2);} else if (left1 != null) {node.left = left1;} else if (left2 != null) {node.left = left2;}}if (right1 != null || right2 != null) {if (right1 != null && right2 != null) {TreeNode right = new TreeNode(right1.val + right2.val);node.right = right;queue.offer(right);queue1.offer(right1);queue2.offer(right2);} else if (right1 != null) {node.right = right1;} else {node.right = right2;}}}return merged;}
}
这段代码同样定义了一个名为 Solution 的类,其中的 mergeTrees 方法用于合并两棵二叉树 t1 和 t2,但与之前的递归解法不同,这里采用的是广度优先搜索(BFS)的方法。具体步骤如下:
-
基本情况检查:
- 首先检查
t1和t2是否为空,与之前一样,如果一方为空,则直接返回另一方。
- 首先检查
-
初始化合并后的树:
- 创建一个新的树节点
merged,其值为t1.val + t2.val。
- 创建一个新的树节点
-
初始化队列:
- 定义三个队列,分别用于存储当前层待处理的合并后节点、
t1的节点和t2的节点。初始时,将merged及其对应的t1和t2根节点分别加入各自的队列。
- 定义三个队列,分别用于存储当前层待处理的合并后节点、
-
广度优先遍历并合并:
- 使用
while循环处理队列,直到queue1和queue2都为空。 - 每次循环,从队列中弹出当前层的
merged节点、t1的节点和t2的节点。 - 对于左子树和右子树,如果有任何一个非空,则创建或直接引用新的节点进行合并:
- 若
t1和t2的子节点都非空,则创建新节点,值为两个子节点的值之和,然后将新节点分别加入合并后的树、queue1和queue2。 - 若只有一个非空,则直接将非空的子节点挂接到合并后的树上。
- 若
- 使用
-
返回合并后的树:
- 遍历完成后,返回最初的合并节点
merged,即合并后的二叉树的根节点。
- 遍历完成后,返回最初的合并节点
这种方法通过层序遍历的方式合并两棵树,同样能有效地合并两棵二叉树,但相比于递归解法,它在处理大量树节点时可能会占用更多内存,因为需要同时维护多个队列来存储每层的节点。不过,它提供了一种迭代而非递归的视角来解决问题,增加了算法实现的多样性。
700. 二叉搜索树中的搜索
给定二叉搜索树(BST)的根节点 root 和一个整数值 val。
你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 null 。
方法一:递归
class Solution {public TreeNode searchBST(TreeNode root, int val) {if (root == null) {return null;}if (val == root.val) {return root;}return searchBST(val < root.val ? root.left : root.right, val);}
}这段代码定义了一个名为 Solution 的类,其中包含一个方法 searchBST。该方法在一个二叉搜索树(BST)中查找值为 val 的节点,并返回找到的节点。如果没有找到,则返回 null。方法使用了递归的方式来实现搜索逻辑。下面是详细的步骤解释:
-
基本情况检查:首先检查当前节点
root是否为空。如果为空,说明树中没有找到值为val的节点,因此返回null。 -
匹配节点值:接下来,比较当前节点
root的值与其要查找的值val。如果两者相等,即找到了目标节点,直接返回当前节点root。 -
选择递归方向:如果当前节点的值不等于
val,则根据 BST 的性质(左子树所有节点的值小于根节点,右子树所有节点的值大于根节点),决定下一步搜索的方向:- 如果
val小于当前节点值root.val,则向左子树 (root.left) 继续搜索。 - 如果
val大于当前节点值root.val,则向右子树 (root.right) 继续搜索。
这里使用了条件运算符(三元运算符)来简洁地表达这一选择逻辑。
- 如果
-
递归调用:根据选择的方向,递归调用
searchBST方法,并将搜索结果返回。由于每次递归调用都更接近目标值或最终确定目标不存在(当遇到空节点时),因此这个过程是逐步缩小搜索范围直至找到目标或遍历完可能的路径。
通过上述递归过程,该方法能够高效地在二叉搜索树中查找指定值的节点。
方法二:迭代
class Solution {public TreeNode searchBST(TreeNode root, int val) {while (root != null) {if (val == root.val) {return root;}root = val < root.val ? root.left : root.right;}return null;}
}这段代码同样定义了一个名为 Solution 的类,其中包含一个方法 searchBST,用于在一个二叉搜索树(BST)中查找值为 val 的节点。与之前的递归实现不同,这里采用的是迭代方法来遍历树并查找目标节点。下面是该方法的详细解释:
-
循环条件与初始化:使用一个
while循环来遍历树,直到找到目标节点或遍历完整个树(即root变为null)。 -
查找并返回匹配节点:在循环体内,首先检查当前节点
root的值是否等于val。如果相等,说明找到了目标节点,直接返回该节点。 -
决定遍历方向:如果当前节点的值不等于
val,根据二叉搜索树的性质选择遍历方向:- 如果
val小于当前节点值root.val,则向左子树移动,即令root = root.left。 - 如果
val大于当前节点值root.val,则向右子树移动,即令root = root.right。
- 如果
-
循环结束:如果循环结束时仍未找到匹配的节点(即
root变为null),则返回null,表示树中不存在值为val的节点。
通过这样的迭代过程,该方法能够高效地在二叉搜索树中查找指定值的节点,且相比递归实现,它在某些情况下(尤其是树深度大时)可以减少调用栈的空间消耗。
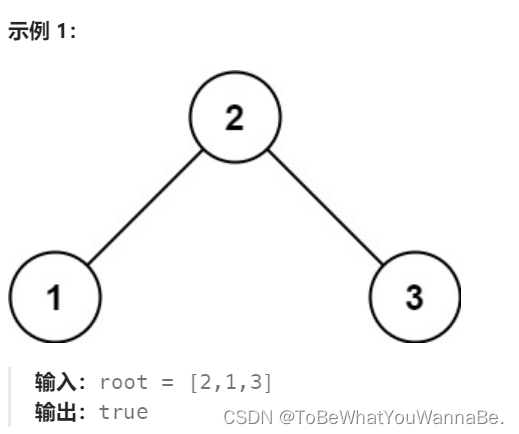
98. 验证二叉搜索树
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
节点的左
子树
只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
方法一: 递归
class Solution {public boolean isValidBST(TreeNode root) {return isValidBST(root, Long.MIN_VALUE, Long.MAX_VALUE);}public boolean isValidBST(TreeNode node, long lower, long upper) {if (node == null) {return true;}if (node.val <= lower || node.val >= upper) {return false;}return isValidBST(node.left, lower, node.val) && isValidBST(node.right, node.val, upper);}
}
这段代码定义了一个名为 Solution 的类,其中包含一个公共方法 isValidBST 用于检查给定的二叉树是否是一棵有效的二叉搜索树(BST)。二叉搜索树的特性是对于任意节点,其左子树中所有节点的值都严格小于该节点的值,其右子树中所有节点的值都严格大于该节点的值。此外,还定义了一个重载的辅助方法 isValidBST,用于递归校验每个节点是否满足BST的条件,并且传递了当前节点值允许的最小值 lower 和最大值 upper 作为边界条件。
具体逻辑如下:
-
公共方法
isValidBST:这是用户调用的接口,接收树的根节点root作为参数。它通过调用重载的辅助方法isValidBST来进行实际的验证工作,初始化lower为Long.MIN_VALUE(Java中的最小长整型值,确保任何合法节点值都大于它),upper为Long.MAX_VALUE(Java中的最大长整型值,确保任何合法节点值都小于它)。 -
辅助方法
isValidBST:- 基本情况:如果当前节点
node为空,说明已遍历到树的底部,返回true表示这一分支是有效的。 - 检查节点值:如果当前节点的值不在允许的范围内(即
node.val <= lower或node.val >= upper),说明违反了BST的规则,返回false。 - 递归验证:对当前节点的左子树和右子树进行递归验证。左子树的每个节点值必须小于当前节点值,因此传递当前节点值作为下一次递归的上限
upper=node.val;右子树的每个节点值必须大于当前节点值,所以传递当前节点值作为下一次递归的下限lower=node.val。只有当左右子树都满足BST条件时,整个树才被认为是有效的BST,因此这里使用逻辑与操作&&连接两个递归调用的结果。
- 基本情况:如果当前节点
通过这样的递归策略,代码能够高效地遍历整个二叉树,同时在每个递归层级上检查节点值是否满足BST的定义,从而确定给定的二叉树是否是一个有效的二叉搜索树。
方法二:中序遍历
class Solution {public boolean isValidBST(TreeNode root) {Deque<TreeNode> stack = new LinkedList<TreeNode>();double inorder = -Double.MAX_VALUE;while (!stack.isEmpty() || root != null) {while (root != null) {stack.push(root);root = root.left;}root = stack.pop();// 如果中序遍历得到的节点的值小于等于前一个 inorder,说明不是二叉搜索树if (root.val <= inorder) {return false;}inorder = root.val;root = root.right;}return true;}
}
这段代码定义了一个名为 Solution 的类,其中包含一个公共方法 isValidBST,用于判断给定的二叉树是否为有效的二叉搜索树(BST)。与之前的递归解法不同,这里采用迭代方法,利用栈来实现中序遍历。下面是代码的详细解析:
-
初始化:声明一个
Deque(双端队列)stack用于存放待访问的节点,以及一个double类型的变量inorder初始化为负无穷大,用于存储中序遍历过程中访问过的节点值(用于检查BST性质)。 -
迭代遍历:使用一个
while循环,条件为栈非空或当前根节点root非空,确保遍历完整个二叉树。-
左子树入栈:在循环内部,首先不断将当前节点
root的左子节点压入栈中,直到没有左子节点,这步是为了确保每次处理的节点都是当前子树的最左节点,即中序遍历的顺序。 -
处理当前节点:当左子节点为空时,从栈顶弹出节点作为当前节点
root,并检查其值是否大于inorder。如果不大于(即小于等于),说明违背了BST的性质(中序遍历下严格递增),直接返回false。 -
更新 inorder:如果当前节点值符合BST性质,则更新
inorder为当前节点值,准备与下一个节点比较。 -
转向右子树:最后,将当前节点更新为其右子节点,继续遍历。
-
-
遍历结束判断:当遍历完整个树(栈为空且当前
root也为空)后,说明所有节点都满足BST的条件,返回true。
这种方法通过迭代实现了二叉树的中序遍历,并在遍历过程中实时检查每个节点的值是否满足BST的定义,是一种空间效率较高的算法,因为它只需要常数级别的额外空间(除了存储树本身的栈空间)。
相关文章:

代码随想录-Day20
654. 最大二叉树 给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建: 创建一个根节点,其值为 nums 中的最大值。 递归地在最大值 左边 的 子数组前缀上 构建左子树。 递归地在最大值 右边 的 子数组后缀上 构建右子树。 返回 nums…...

揭秘C++ String容器:字符串操作的艺术
目录 编辑 引言 一、初识std::string:构造与初始化 二、字符串的操纵艺术:拼接、查找与替换 三、访问与遍历:字符的细腻触感 四、大小与容量:动态调整的智慧 五、进阶功能:探索更多可能 结语 引言 在C标准库…...

【C++】牛客 ——DP36 abb
✨题目链接: DP36 abb ✨题目描述 leafee 最近爱上了 abb 型语句,比如“叠词词”、“恶心心” leafee 拿到了一个只含有小写字母的字符串,她想知道有多少个 "abb" 型的子序列? 定义: abb 型字符串满足以下…...

SpringBoot如何实现跨域?
定义一个配置类,实现WebMvcConfigurer接口,重写addCorsMappings方法 Configuration public class CorsConfig implements WebMvcConfigurer {Overridepublic void addCorsMappings(CorsRegistry registry) {registry.addMapping("/**").allow…...

SW 草图偏移 先预选
因为有些不能用链全部选,可以先框选要偏移的,再点偏移命令...

5.23 Linux中超时检测方式+模拟面试
1.IO多路复用的原理? IO多路复用使得一个或少量线程资源处理多个连接的IO事件的技术。对于要处理的多个阻塞的IO操作,建立集合并存储它们的文件描述符,利用单个阻塞函数去监控集合中文件描述符事件到达的情况,(如果到…...

MySQL数据表索引命名规范
在数据库设计和开发过程中,索引是提高查询性能的重要工具。合理的索引命名规范不仅能提高代码的可读性,还能便于维护和管理。本文将详细介绍MySQL数据表索引的命名规范,包括不同类型索引的命名方法,并提供多个代码示例以说明如何命…...

python内置函数map/filter/reduce详解
在Python中,map(), filter(), 和 reduce() 是内置的高级函数(实际是class),用于处理可迭代对象(如列表、元组等)的元素。这些函数通常与lambda函数一起使用,以简洁地表达常见的操作。下面我将分别解释这三个函数。 1. …...

PICO VR眼镜定制播放器使用说明文档videoplayerlib-ToB.apk
安装高级定制播放器 高级定制播放器下载地址:https://download.csdn.net/download/ahphong/89360454 仅限用于PICO G2、G3、G4、NEO系列VR眼镜上使用, 用途:用于第三方APP(开发者)调用定制播放器播放2D、3D、180、360全景视频。 VR眼镜系统请升级到最新版,可在官网下载,…...
基于51单片机的超声波液位测量与控制系统
基于51单片机液位控制器 (仿真+程序+原理图PCB+设计报告) 功能介绍 具体功能: 1.使用HC-SR04测量液位,LCD1602显示; 2.当水位高于设定上限的时候,对应声光报警报警&am…...
详细分析Element中的MessageBox基本知识(附Demo)
目录 前言1. 基本知识2. Demo2.1 确认框2.2 警告框2.3 对话框 3. this.$confirm 前言 详细知识推荐阅读:详细分析Element Plus中的ElMessageBox弹窗用法(附Demo及模版) MessageBox则常用于Vue2 1. 基本知识 MessageBox 是 Element UI 提供…...
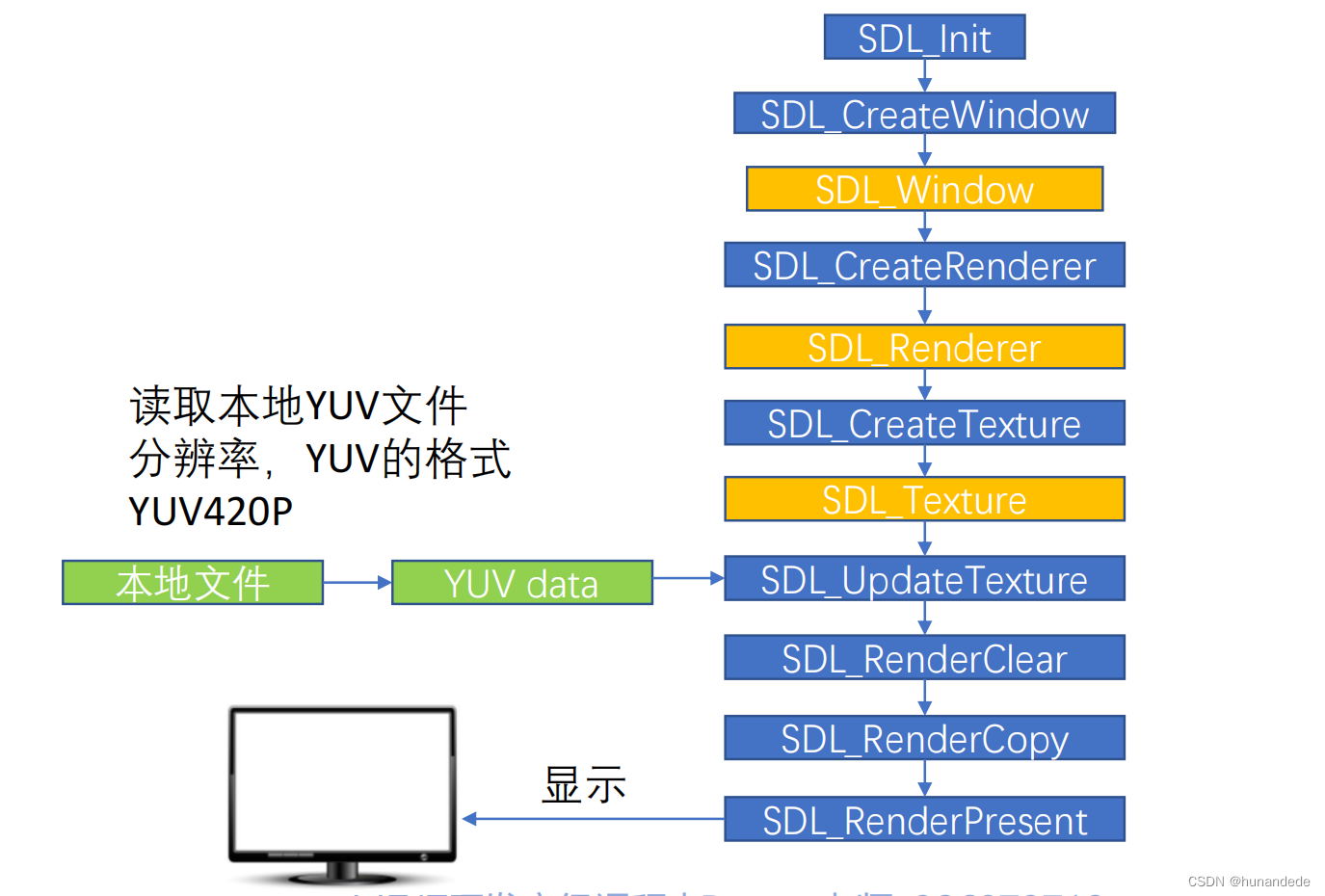
音视频开发8 音视频中SDL的使用,SDL 在windows上环境搭建,SDL 使用 以及 常用 API说明,show YUV and play PCM
1.SDL简介 SDL(Simple DirectMedia Layer),是一个跨平台的C语言多媒体开发库。 支持Windows、Mac OS X、Linux、iOS、Android 提供对音频、键盘、鼠标、游戏操纵杆、图形硬件的底层访问 很多的视频播放软件、模拟器、受欢迎的游戏都在使用…...

P1003 [NOIP2011 提高组] 铺地毯
题目传送门: P1003 [NOIP2011 提高组] 铺地毯 AC代码: #include<bits/stdc.h>using namespace std;int a[10005],b[10005],g[10005],k[10004];int main() {int n,x,y;cin>>n;for(int i1;i<n;i) cin>>a[i]>>b[i]>>g[…...

C语言学习笔记之指针(一)
目录 什么是指针? 指针和指针类型 指针的类型 指针类型的意义 指针-整数 指针的解引用 指针 - 指针 指针的关系运算 野指针 什么是野指针? 野指针的成因 如何规避野指针? 二级指针 什么是指针? 在介绍指针之前&#…...
化学中的不确定性。
化学中的不确定性TOC 基于元素分析的无机化学的理论大厦应该说早已落成了,但是却仍然存在着一些列的难解甚至是无解问题,这些大多是在使用理论解释现象时遇到的困难,有些则是在生产实践中生产工艺和生产工序设计和优化中发现的问题。于是&…...

AWS容器之Fargate
AWS Fargate是亚马逊提供的一种容器管理服务,它允许开发人员在AWS云中轻松运行容器化应用程序,而无需管理底层的服务器基础架构。Fargate可以自动管理容器的部署、扩展和负载平衡,并提供了与ECS和EKS等AWS容器服务集成的能力。适用于容器的无…...

C#面:DataReader与Dataset有什么区别
C#中的DataReader和DataSet都是用于处理数据的类,但它们有一些区别。 DataReader是一种轻量级的只进只读数据流,用于从数据库中检索数据。它是一种快速且高效的数据访问方式,适用于大量数据的读取。DataReader一次只能读取一行数据ÿ…...

操作系统课程实验1-进程调度模拟实验
操作系统课程实验1-进程调度模拟实验 一、实验介绍 1.1 实验目的 本实验模拟在单处理机环境下的处理机调度,帮助理解进程调度的概念,深入了解进程控制块的功能,以及进程的创建、撤销和进程各个状态间的转换过程。 1.2 实验内容 进程调度算…...

JVM CMS 在Full GC时针对跨代引用的优化
个人博客 JVM CMS 在Full GC时针对跨代引用的优化 | iwts’s blog 跨代引用问题 Full GC慢的一个很重要的问题:跨代引用。 简单描述就是: 现代JVM一般是根据对象存活的特性进行了分代,提高了垃圾收集的效率。但是像在回收新生代的时候&a…...

【Makefile】Makefile 编译 Keil 工程(Linux 环境)
本文使用的开发板为 stm32f103C8T6,使用的驱动库为stm32标准库。 目录 一、软件下载 1、stm32 标准库 2、arm-none-eabi 工具链 3、烧录器 二、Keil 工程改造 1、Keil 工程 2、基本 Makefile 工程 3、添加启动文件 4、添加链接脚本 5、去掉 core_cm3.c 三…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

AD学习(3)
1 PCB封装元素组成及简单的PCB封装创建 封装的组成部分: (1)PCB焊盘:表层的铜 ,top层的铜 (2)管脚序号:用来关联原理图中的管脚的序号,原理图的序号需要和PCB封装一一…...
