【机器学习】期望最大化(EM)算法
文章目录
- 一、极大似然估计
- 1.1 基本原理
- 1.2 举例说明
- 二、Jensen不等式
- 三、EM算法
- 3.1 隐变量 与 观测变量
- 3.2 为什么要用EM
- 3.3 引入Jensen不等式
- 3.4 EM算法步骤
- 3.5 EM算法总结
- 参考资料
EM是一种解决 存在隐含变量优化问题 的有效方法。EM的意思是“期望最大化(Expectation Maximization)” 。EM是解决(不完全数据,含有隐变量)最大似然估计(MLE)问题的迭代算法 。
EM算法有很多的应用,最广泛的就是混合高斯模型GMM、隐马尔可夫模型HMM、贝叶斯网络模型等等。
在介绍具体的EM算法前,我们先介绍 极大似然估计 和 Jensen不等式。
一、极大似然估计
极大似然估计法是一种求估计的统计方法,它建立在极大似然原理的基础之上。
1.1 基本原理
极大似然估计的原理是:一个随机试验如有若干个可能的结果A,B,C,…。若在一次试验中,结果A出现,则一般认为试验条件对A出现有利,也即A出现的概率很大。极大似然估计就是利用已知的样本结果,反推最有可能(最大概率)导致这样结果的参数值。 这也是统计学中用样本估计整体的一种阐述。

1.2 举例说明
【任务】:估计某个学校的男生的身高分布。 假设你在校园里随便找了100个男生,他们的身高是服从高斯分布的。但是这个分布的均值u和方差σ我们不知道,记作 θ = [ u , σ ] θ=[u, σ] θ=[u,σ]。
【问题】:我们知道样本所服从的概率分布的模型和一些样本,而不知道该模型中的参数?
【如何估计】:
- 样本集 X = x 1 , x 2 , … , x N X={x_1,x_2,…,x_N} X=x1,x2,…,xN,其中 N=100
- 概率密度: p ( x i ∣ θ ) p(x_i|θ) p(xi∣θ) 为抽到男生i(的身高)的概率。 100个样本之间独立同分布,所以我同时抽到这100个男生的概率就是他们各自概率的乘积。就是从分布是 p ( x ∣ θ ) p(x|θ) p(x∣θ) 的总体样本中抽取到这100个样本的概率,也就是样本集X中各个样本的联合概率,用下式表示:
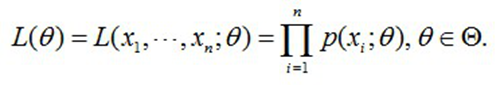
上式反映了在概率密度函数的参数是θ时,得到X这组样本的概率。
需要找到一个参数θ,其对应的似然函数L(θ)最大,也就是说抽到这100个男生(的身高)概率最大。这个叫做θ的最大似然估计量,记为:

【求解步骤】:
- 首先,写出似然函数:
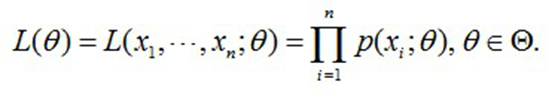
- 然后,对似然函数取对数:
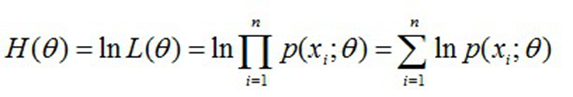
- 求导数,令导数为0,得到似然方程;
- 最后,解似然方程,得到的参数即为所求。
【总结】:
极大似然法:知道样本所服从的概率分布模型,而不知道该模型中的参数,需要求参数。
具体步骤如下:
- 已知概率模型,根据概率密度函数写出联合概率(似然函数);
- 对似然函数取对数;
- 求导。令导数等于0,求出参数。
注意:这里是通过求导来实现求解。若是求导不好解,可以在似然函数前面乘以负值,改写成最小化目标函数,然后用梯度下降法求解。具体可以参考logistic regression的求解方法。
多数情况下我们是根据已知条件来推算结果,而极大似然估计是已经知道了结果,然后寻求使该结果出现的可能性最大的条件,以此作为估计值。
二、Jensen不等式
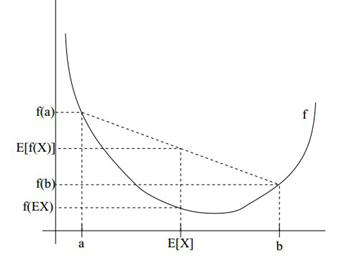
设f是定义域为实数的函数,如果对于所有的实数x。如果对于所有的实数x,f(x)的二次导数大于等于0,那么f是凸函数。
Jensen不等式表述如下:如果f是凸函数,X是随机变量,那么:E[f(X)]>=f(E[X])。当且仅当X是常量时,上式取等号。
三、EM算法
【任务】:估计某个学校的男生和女生的身高分布。 我们抽取了100个男生和100个女生样本的身高,但是我们不知道每一个人到底是从男生还是女生的身高分布中抽取的。
用数学的语言就是,抽取得到的每个样本都不知道是从哪个分布抽取的。 这个时候,对于每一个样本,就有两个东西需要猜测或者估计:
(1)这个人是男的还是女的?
(2)男生和女生对应的身高的高斯分布的参数?
EM算法要解决的问题是:
(1)求出每一个样本属于哪个分布
(2)求出每一个分布对应的参数
如果把这个数据集的概率密度画出来,大约是这个样子:
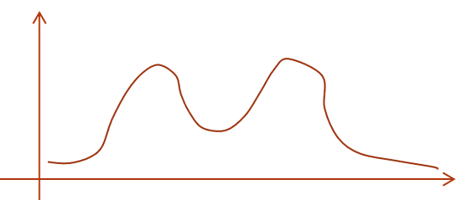
其实这个双峰的概率密度函数是有模型的,称作混合高斯模型(GMM)。GMM其实就是k个高斯模型加权组成,α是各高斯分布的权重,Θ是参数。
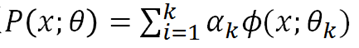
对GMM模型的参数估计,就要用EM算法。更一般的讲,EM算法适用于带有隐变量的概率模型的估计。
3.1 隐变量 与 观测变量
首先给出观测变量与隐变量的定义:
- 观测变量: 模型中可以直接观测,即在研究中能够收集到的变量成为观测变量。
- 隐变量: 模型中不可观测的随机变量,我们通常通过可观测变量的样本对隐变量作出推断。
在上述例子中,隐变量就是对每一个身高而言,它属于男生还是女生。
3.2 为什么要用EM
我们来具体考虑一下上面这个问题。如果使用极大似然估计(这是我们最开始最单纯的想法),那么我们需要极大化的似然函数应该是这个:
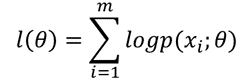
然而我们并不知道p(x;θ)的表达式。这里考虑隐变量,如果我们已经知道哪些样本来自男生,哪些样本来自女生。用Z=0或Z=1标记样本来自哪个总体,则Z就是隐变量,需要最大化的似然函数就变为:
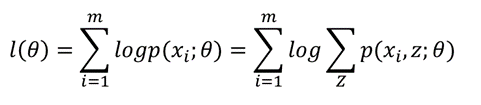
然而我们并不知道隐变量的取值。要估计一个样本是属于男生还是女生,我们就要有模型参数,要估计模型参数,我们首先要知道一个样本属于男生还是女生的可能性。(鸡生蛋,蛋生鸡)
这里,我们利用假设来求解:
- 首先假设一个模型参数θ,然后每个样本属于男生还是女生的概率p(zi)就能算出来了,p(xi,zi)=p(xi|zi)p(zi)。而x|z=0服从女生身高分布,x|z=1服从男生身高分布,所以似然函数可以写成含有θ的函数,极大化它我们可以得到一个新的θ。
- 新的θ因为考虑了样本来自哪个分布,会比原来的更能反应数据规律。有了这个更好的θ我们再对每个样本重新计算它属于男生还是女生的概率,用更好的θ算出来的概率会更准确。
- 有了更准确的信息,我们可以继续像上面一样估计θ,自然而然这次得到的θ会比上一次更棒,如此直到收敛(参数变动不明显了)。
实际上,EM算法就是这么做的。
事实上,隐变量估计问题也可以通过梯度下降等优化算法求解,但由于求和的项数将随着隐变量的数目以指数级上升,会给梯度计算带来麻烦。而EM算法则可以看作是一种非梯度优化方法。
3.3 引入Jensen不等式
然而事情并没有这么简单,上面的思想理论上可行,实践起来不成。主要是因为似然函数有“和的log”这一项,log里面是一个和的形式,求导复杂。直接强来你要面对 “两个正态分布的概率密度函数相加”做分母,“两个正态分布分别求导再相加”做分子的分数形式。m个这玩意加起来令它等于0,要求出关于θ的解析解,你对自己的数学水平想的不要太高。此处,考虑到Jensen不等式,有
直接最大化似然函数做不到,那么如果我们能找到似然函数的一个紧的下界一直优化它,并保证每次迭代能够使总的似然函数一直增大,其实也是一样的。(利用紧下界迭代逼近)
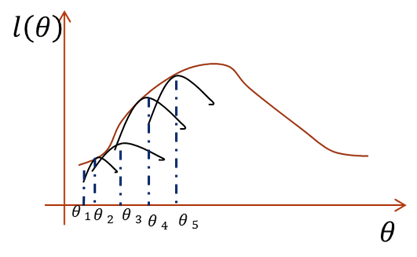
横坐标是参数,纵坐标是似然函数,首先我们初始化一个θ1,根据它求似然函数一个紧的下界,也就是图中第一条黑短线。黑短线上的值虽然都小于似然函数的值,但至少有一点可以满足等号(所以称为紧下界),最大化小黑短线我们就hit到至少与似然函数刚好相等的位置,对应的横坐标就是我们的新的θ2。如此进行,只要保证随着θ的更新,每次最大化的小黑短线值都比上次的更大,那么算法收敛,最后就能最大化到似然函数的极大值处。
构造这个小黑短线,就要靠Jensen不等式。注意我们这里的log函数是个凹函数,所以我们使用的Jensen不等式的凹函数版本。根据Jensen函数,需要把log里面的东西写成数学期望的形式,注意到log里的和是关于隐变量Z的和。于是,这个数学期望一定是和Z有关,如果设Q(z)是Z的分布函数,那么可以这样构造:
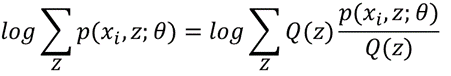
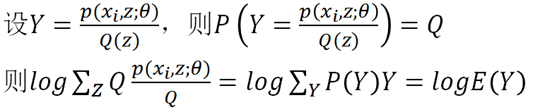
所以log里其实构造了一个随机变量Y,Y是Z的函数,Y取p/Q的值的概率是Q。构造好数学期望,下一步根据Jensen不等式进行放缩:
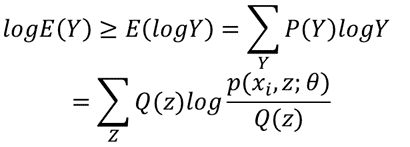
有了这一步,我们看一下整个式子:
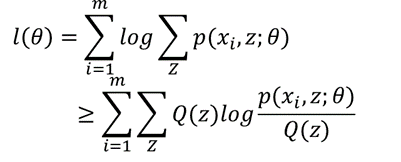
也就是说我们找到了似然函数的一个下界,那么优化它是否就可以呢?不是的,上面说了必须保证这个下界是紧的,也就是至少有点能使等号成立。由Jensen不等式,等式成立的条件是随机变量是常数,具体就是:
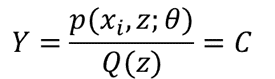
又因为Q(z)是z的分布函数,所以:
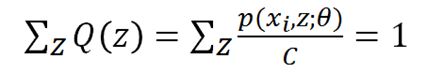
把C乘过去,可得C就是p(xi,z)对z求和,所以我们终于知道了:
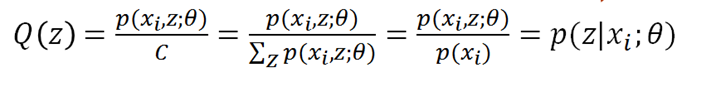
得到Q(z),大功告成。Q(z)就是p(zi|xi),或者写成p(zi),代表第i个数据是来自zi的概率。
3.4 EM算法步骤
初始化分布参数θ,重复以下步骤直到收敛:
1. E-Step:根据参数初始值或上一次迭代的模型参数来计算出隐性变量的后验概率,其实就是隐性变量的期望。 作为隐变量的现估计值。(根据参数θ计算每个样本属于zi的概率,即这个身高来自男生或女生的概率)
2. M-Step:将似然函数最大化以获得新的参数值。 根据计算得到的Q,求出含有θ的似然函数的下界并最大化它,得到新的参数θ。
3.5 EM算法总结
- EM算法是一种从不完全数据或有数据丢失的数据集(存在隐变量)中求解概率模型参数的最大似然估计方法。
- 第一步求隐变量的期望(E)
- 第二步求似然函数极大(M)
- EM算法在一般情况是收敛的,但是不保证收敛到全局最优,即有可能进入局部的最优。
- 应用到的地方:混合高斯模型GMM、隐马尔科夫模型HMM、贝叶斯网络模型等。
参考资料
- 【机器学习】EM算法详细推导和讲解
相关文章:
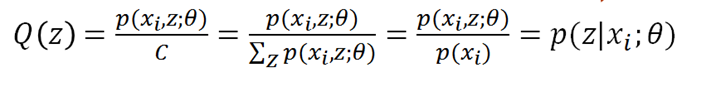
【机器学习】期望最大化(EM)算法
文章目录 一、极大似然估计1.1 基本原理1.2 举例说明 二、Jensen不等式三、EM算法3.1 隐变量 与 观测变量3.2 为什么要用EM3.3 引入Jensen不等式3.4 EM算法步骤3.5 EM算法总结 参考资料 EM是一种解决 存在隐含变量优化问题 的有效方法。EM的意思是“期望最大化(Exp…...

【Python】机器学习中的过采样和欠采样:处理不平衡数据集的关键技术
原谅把你带走的雨天 在渐渐模糊的窗前 每个人最后都要说再见 原谅被你带走的永远 微笑着容易过一天 也许是我已经 老了一点 那些日子你会不会舍不得 思念就像关不紧的门 空气里有幸福的灰尘 否则为何闭上眼睛的时候 又全都想起了 谁都别说 让我一个人躲一躲 你的承诺 我竟然没怀…...
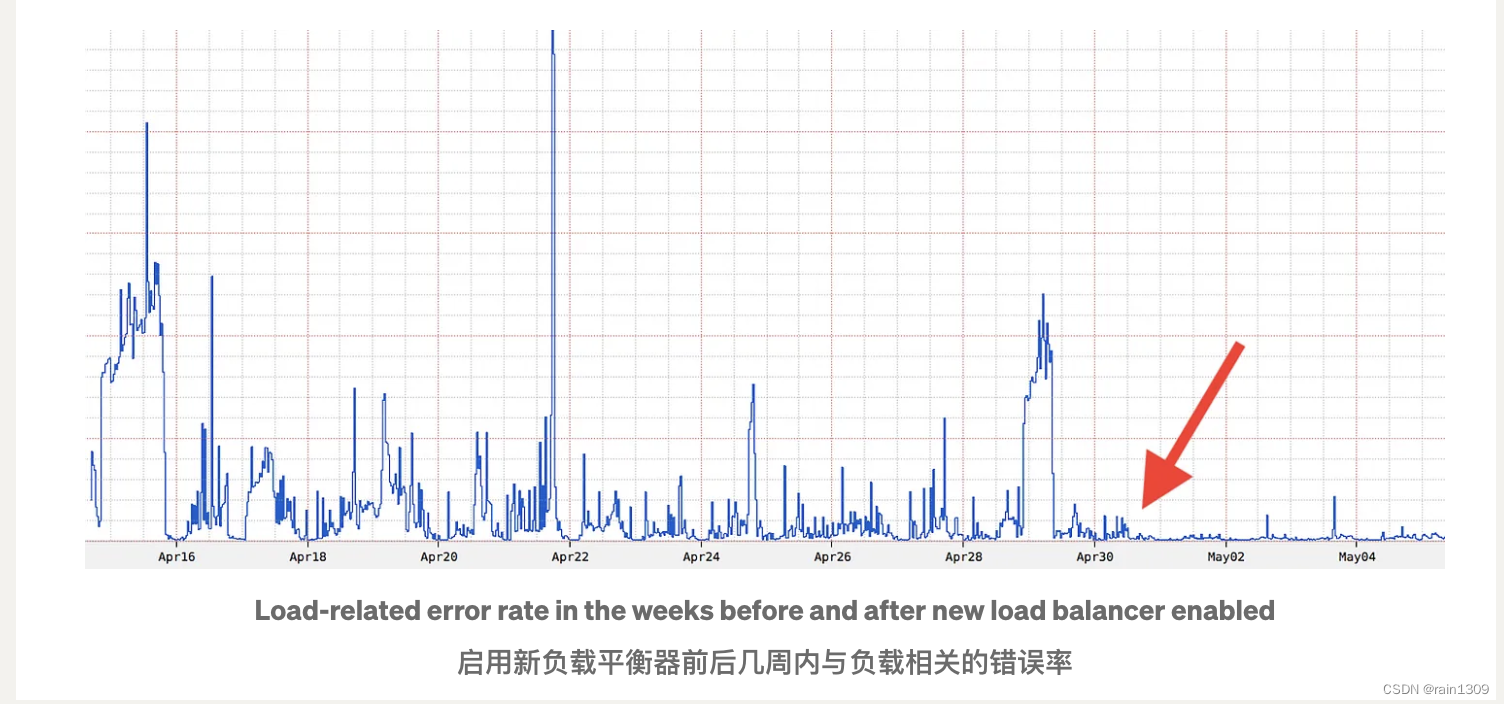
重新思考:Netflix 的边缘负载均衡
声明 本文是对Netflix 博客的翻译 前言 在先前关于Zuul 2开源的文章中,我们简要概述了近期在负载均衡方面的一些工作。在这篇文章中,我们将更详细地介绍这项工作的原因、方法和结果。 因此,我们开始从Zuul和其他团队那里学习&#…...

元组的创建和删除
目录 使用赋值运算符直接创建元组 创建空元组 创建数值元组 删除元组 自学python如何成为大佬(目录):https://blog.csdn.net/weixin_67859959/article/details/139049996?spm1001.2014.3001.5501 元组(tuple)是Python中另一个重要的序列结构&#…...

CSS3用户界面
用户界面 appearance appearance 属性用于控制元素是否采用用户代理(浏览器)的默认样式(外观) element {appearance: auto | none;}auto(默认):元素采用浏览器提供的默认样式。none:元素不采用任何默认样式,显示为“裸”元素,通常表现为无特定样式的简单框。input[…...

STL源码刨析:序列式容器之vector
目录 1.序列式容器和关联式容器 2.vector的定义和结构 3.vector的构造函数和析构函数的实现 4.vector的数据结构以及实现源码 5.vector的元素操作 前言 本系列将重点对STL中的容器进行讲解,而在容器的分类中,我们将容器分为序列式容器和关联式容器。本章…...

Flutter 中的 AbsorbPointer 小部件:全面指南
Flutter 中的 AbsorbPointer 小部件:全面指南 在Flutter中,AbsorbPointer是一个特殊的小部件,用于吸收(或“吞噬”)所有传递到其子组件的指针事件(如触摸或鼠标点击)。这在某些情况下非常有用&…...

Web开发学习总结
学习路线 Web 全球广域网,也称为万维网(www World Wide Web),能够通过浏览器访问的网站 初识Web前端 Web标准也称为网页标准,由一系列的标准组成,大部分由W3C(World Wide Web Consortium,万维网联盟)负责制定。三个组…...

springboot相关知识集锦----1
一、springboot是什么? springboot是一个用于构建基于spring框架的独立应用程序的框架。它采用自动配置的原则,以减少开发人员在搭建应用方面的时间和精力。同时提升系统的可维护性和可扩展性。 二、springboot的优点 约定优于配置 版本锁定…...
App推广新境界:Xinstall助你轻松突破运营痛点,实现用户快速增长!
在移动互联网时代,App已经成为企业营销不可或缺的一部分。然而,如何有效地推广App,吸引并留住用户,成为了众多企业面临的难题。今天,我们将为您揭秘一款神奇的App推广工具——Xinstall,它将助您轻松突破运营…...
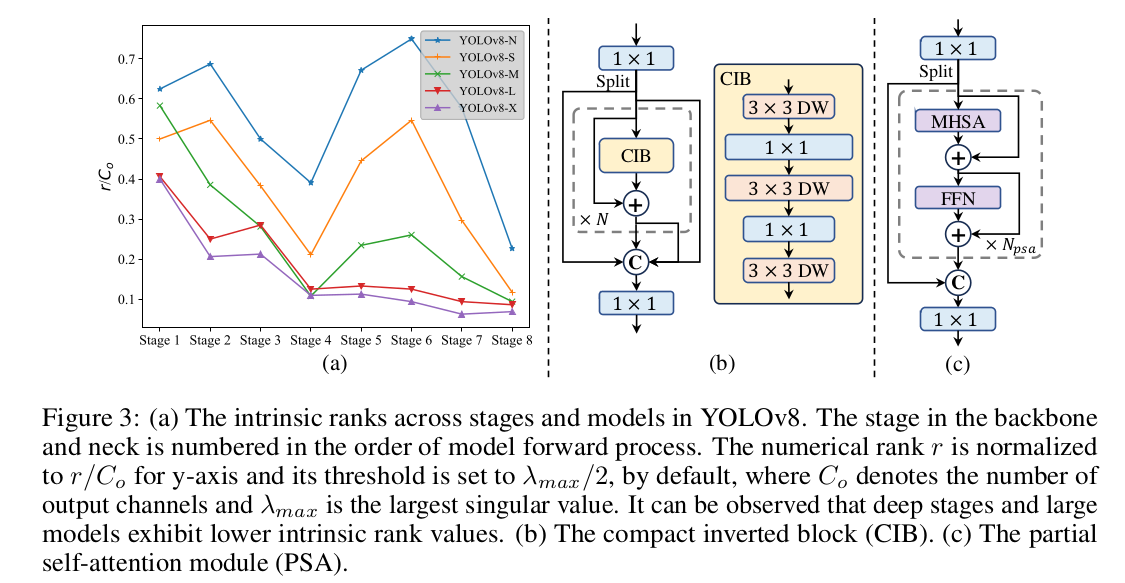
YOLOv10 论文学习
论文链接:https://arxiv.org/pdf/2405.14458 代码链接:https://github.com/THU-MIG/yolov10 解决了什么问题? 实时目标检测是计算机视觉领域的研究焦点,目的是以较低的延迟准确地预测图像中各物体的类别和坐标。它广泛应用于自动…...
[Spring Boot]baomidou 多数据源
文章目录 简述本文涉及代码已开源 项目配置pom引入baomidouyml增加dynamic配置启动类增加注解配置结束 业务调用注解DS()TransactionalDSTransactional自定义数据源注解MySQL2 测试调用查询接口单数据源事务测试多数据源事务如果依然使用Transactional会怎样?测试正…...

Drone+Gitee自动执行构建、测试和发布工作流
拉取Drone:(至于版本,你可以下载最新的) sudo docker pull drone/drone:2 拉取runner: sudo docker pull drone/drone-runner-docker 在Gitee中添加第三方应用: 进入个人主页,点击设置: 往下翻,找到数…...

Unity3D MMORPG 主城角色动画控制与消息触发详解
Unity3D是一款强大的游戏开发引擎,它提供了丰富的功能和工具,使开发者能够轻松创建出高质量的游戏。其中,角色动画控制和消息触发是游戏开发中非常重要的一部分,它们可以让游戏角色表现出更加生动和多样的动作,同时也能…...

【Text2SQL 经典模型】HydraNet
论文:Hybrid Ranking Network for Text-to-SQL ⭐⭐⭐ arXiv:2008.04759 HydraNet 也是利用 PLM 来生成 question 和 table schema 的 representation 并用于生成 SQL,并在 SQLova 和 X-SQL 做了改进,提升了在 WikiSQL 上的表现。 一、Intro…...
Mysql-根据字段名查询字段在哪些表里
SELECT * FROM information_schema.COLUMNS WHERE COLUMN_NAMElabel_name;...

牛逼!50.3K Star!一个自动将屏幕截图转换为代码的开源工具
1、背景 在当今快节奏的软件开发环境中,设计师与开发者之间的协同工作显得尤为重要。然而,理解并准确实现设计稿的意图常常需要耗费大量的时间和沟通成本。为此,开源社区中出现了一个引人注目的项目——screenshot-to-code,它利用…...

八种单例模式
文章目录 1.单例模式基本介绍1.介绍2.单例模式八种方式 2.饿汉式(静态常量,推荐)1.基本步骤1.构造器私有化(防止new)2.类的内部创建对象3.向外暴露一个静态的公共方法 2.代码实现3.优缺点分析 3.饿汉式(静态…...

禅道密码正确但是登录异常处理
禅道密码正确,但是登录提示密码错误的异常处理 排查内容 # 1、服务器异常,存储空间、数据库异常 # 2、服务异常,文件丢失等异常问题定位 # 1、df -h 排查服务器存储空间 # 2、根据my.php排查数据库连接是否正常 # 3、修改my.pho,debugtrue…...

Go微服务: Nacos的搭建和基础API的使用
Nacos 概述 文档:https://nacos.io/docs/latest/what-is-nacos/搭建:https://nacos.io/docs/latest/quickstart/quick-start-docker/有很多种搭建方式,我们这里使用 docker 来搭建 Nacos 的搭建 这里,我们选择单机模式…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...
