如何理解kmp的套娃式算法啊?
概念
KMP算法,全称Knuth Morris Pratt算法 。文章大部分内容出自《数据结构与算法之美》
核心思想
假设主串是a,模式串是b
在模式串与主串匹配的过程中,当遇到不可匹配的字符的时候,对已经对比过的字符,是否能找到一种规律,将模式串一次性滑动多位,跳过那些肯定不会匹配的情况?
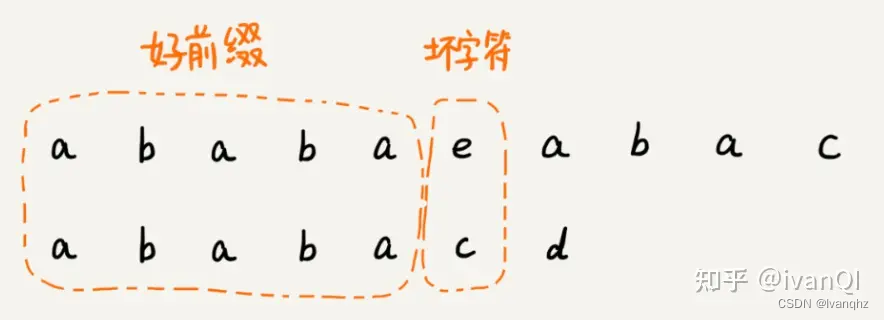
这里可以类比一下,在模式串和主串匹配的过程中,把不能匹配的那个字符仍然叫做坏字符,把已经匹配的那段字符串叫做好前缀
当遇到坏字符的时候,就要把模式串往后滑动,在滑动的过程中,只要模式串和好前缀有上下重合,前面几个字符比较,就相当于拿好前缀的后缀子串,跟模式串的前缀子串在比较
KMP目的
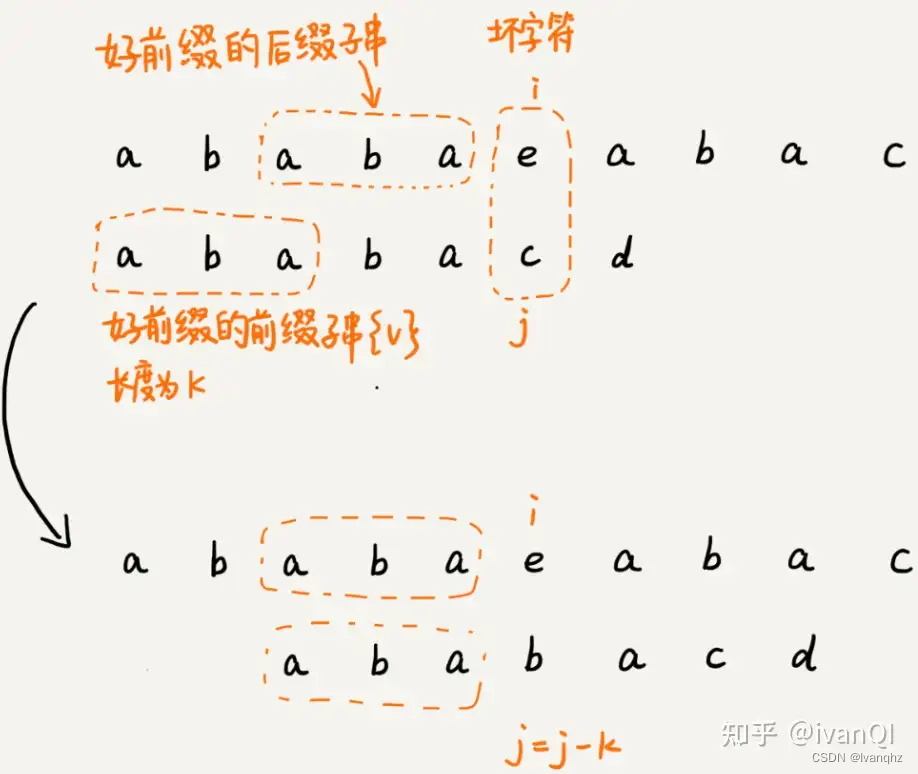
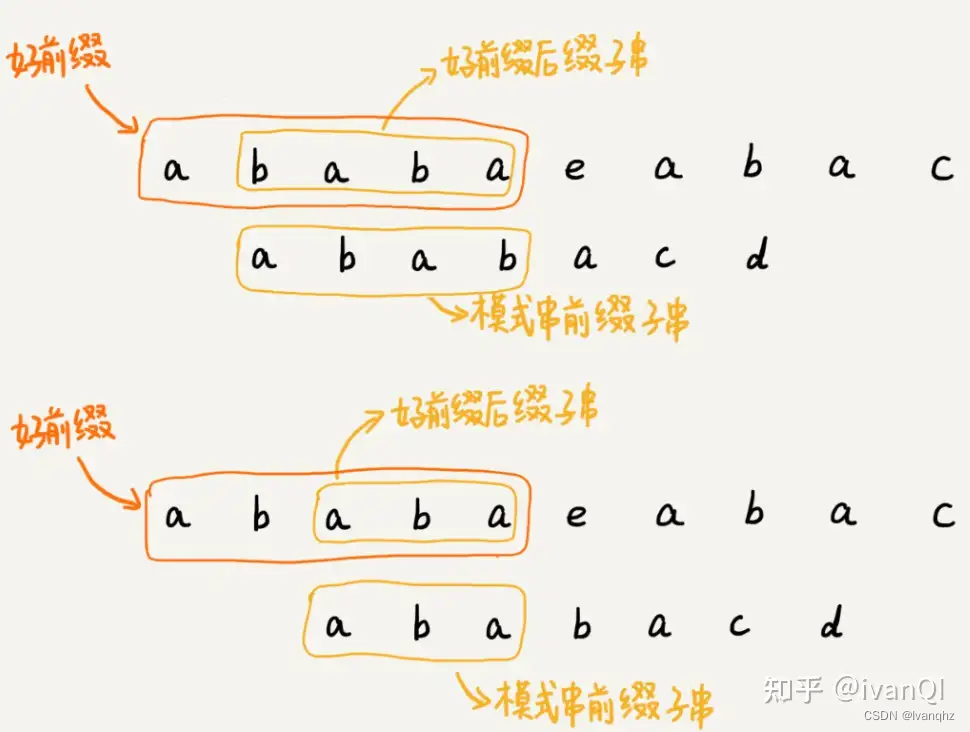
只需要拿好前缀本身,在它的后缀子串中,查找最长的那个可以跟好前缀匹的前缀子串匹配
假设最长的可匹配的那部分前缀子串{v}, 长度为k
可以把模式串一次性往后滑动j - k位,相当于,每次遇到坏字符的时候,就把j 更新为k。i不变。然后比较
最长可匹配后缀子串 && 最长可匹配前缀子串
把好前缀的所有后缀子串中,最长的可匹配前缀子串的那个后缀子串,叫作最长可匹配后缀子串
对应的前缀子串,叫作最长可匹配前缀子串

为什么求最长可匹配子串前缀和后缀子串,为什么不涉及主串,只需通过模式串就能求解?
以上图所示,好前缀的定义是主串和模式串匹配的部分
所以好后缀的最长可匹配子串必然会落到模式串中,所以用模式串求最长可匹配的前缀和后缀子串
失效函数(next 数组)
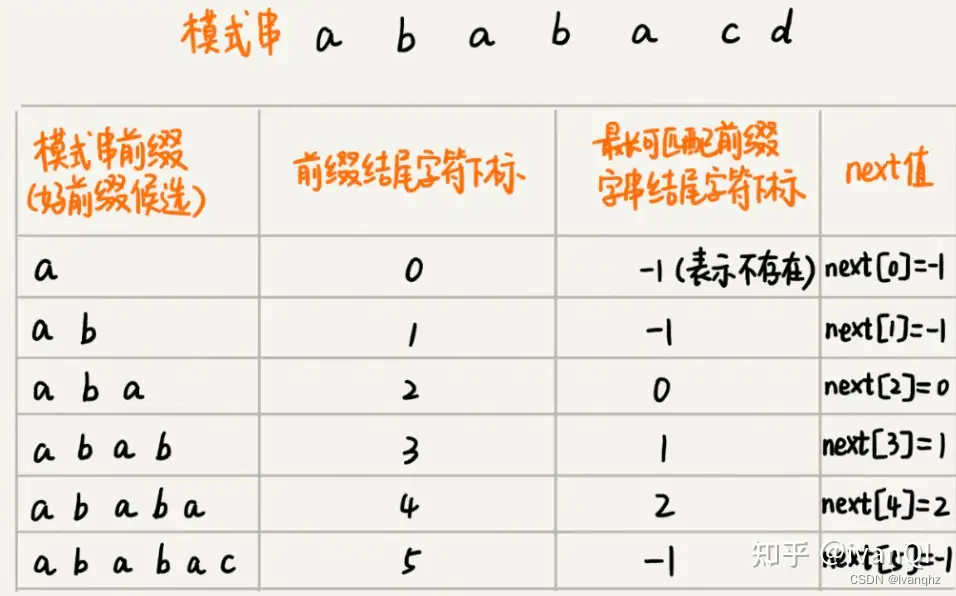
数组的下标是每个前缀结尾字符下标,数组的值是这个
前缀的最长可以匹配前缀子串的结尾字符下标
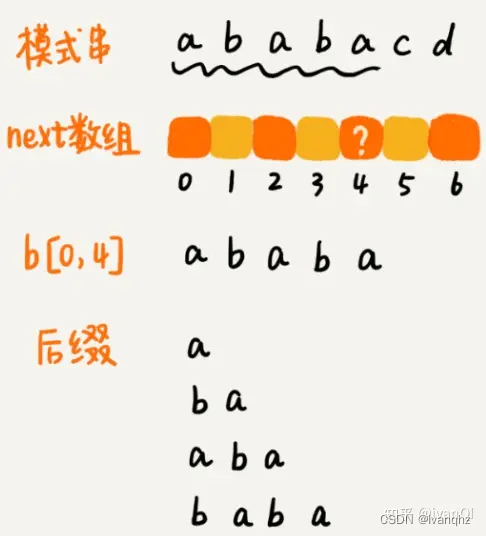
例子:ababacd
- 前缀列表访问顺序:从右到左
- 后缀列表访问顺序:从左到右
过程
1. a: 无匹配,下标为-1
2. ab: 无匹配,下标为-1
3. aba: 匹配1个字符。下标为0前缀: a ab后缀: ba a
4. abab,匹配2个字符,下标为1前缀:a ab aba后缀:bab ab b
5. ababa,匹配3个字符,下标为2前缀:a ab aba abab后缀:baba aba ab a
6. ababac,无匹配,下标为-1前缀:a ab aba abab ababa后缀:babac abac bac ac c
7. ababacd,无匹配,下标为-1前缀:a ab aba abab ababa ababac后缀:babacd abacd bacd acd cd c
next数组的计算
暴力计算方法
暴力求解子串,效率低
把所有后缀子串从长到短找出来,依次看能否匹配前缀
类动态规划方法(k:最长前后缀子串)
若p[k] == p[i]
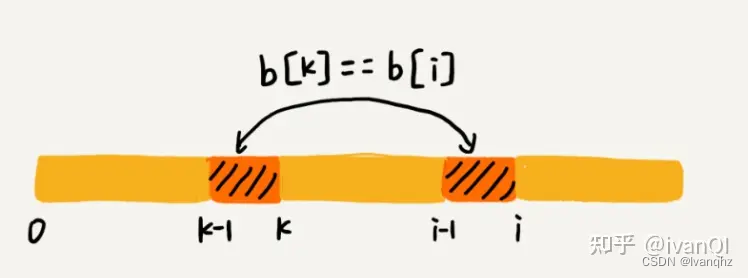
如果 next[i - 1] = k - 1,那么子串 b[0, k - 1] 是 b[0, i - 1]最长可匹配前缀子串
如果子串 b[0, k - 1] 的下一个字符 b[k],与 b[0, i -1 ]的下一个字符 b[i] 匹配,那子串 b[0, k]就是 b[0, i]的最长可匹配前缀子串
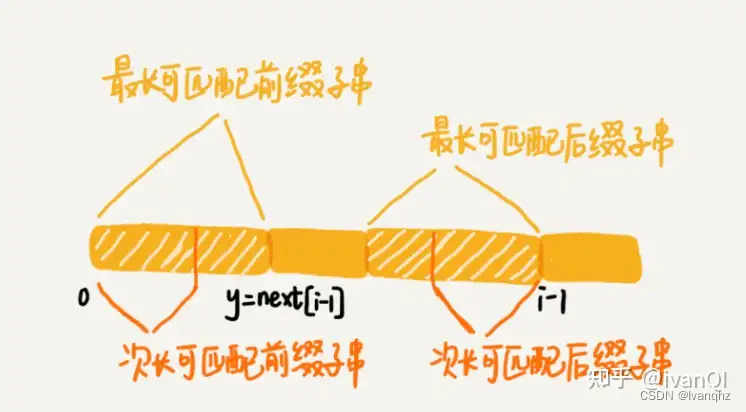
若p[k] ≠ p[i]
假设最长可匹配前缀 k
如果 p[k] ≠ p[i]。则需要次最大匹配前缀 p[next[k]].
如果 p[next[k]] ≠ p[i]. 则需要次次最大匹配前缀。直到匹配成功,或者匹配失败

代码地址
数据结构和算法
时间复杂度
构建next数组
void getNext(char *p, int p_len, int *next) {next[0] = -1;int k = -1;int i;for (i = 1; i < p_len; ++i) {while (k != -1 && p[k + 1] != p[i]) {k = next[k];}if (p[k + 1] == p[i]) {++k;}next[i] = k;}}
i 从1开始一直增加到p_len,而k并不是每次for循环都增加,所以,k累积增加的值肯定小于 p_len
而while循环中的 k = next[k],实际上是在减小k的值,k累积都没有增加超过p_len.所以while循环总数也不会超过p_len
这部分时间复杂度: O(p_len)
借助next数组匹配
int kmp(char *s, int s_len, char *p, int p_len) {int next[p_len];getNext(p, p_len, next);int j = 0;int i;for (i = 0; i < s_len; ++i) {while (j > 0 && s[i] != p[j]) { // 一直找到s[i] 和 p[j]j = next[j - 1] + 1;}if (s[i] == p[j]) ++j;if (j == p_len) { // 找到匹配模式串return i - p_len + 1;}}return -1;
}
i 从0循环增加到 s_len - 1, j的增长量不可能超过i,所以肯定小于s_len
而while 循环中的那条 j = next[j - 1] + 1; 不会让 j增长
所以,这部分的时间复杂度为O(s_len)
总时间复杂度: O(s_len + p_len)
空间复杂度
KMP只需要一个额外的next数组,数组的大小跟模式串相同
空间复杂度:O(p_len), p_len表示模式串长度
相关文章:

如何理解kmp的套娃式算法啊?
概念 KMP算法,全称Knuth Morris Pratt算法 。文章大部分内容出自《数据结构与算法之美》 核心思想 假设主串是a,模式串是b 在模式串与主串匹配的过程中,当遇到不可匹配的字符的时候,对已经对比过的字符,是否能找到…...

python中树的运用样例
目录 一、文件系统样例 二、Trie树 一、文件系统样例 class FileNode:def __init__(self, name, is_fileFalse):self.name nameself.is_file is_fileself.children []def add_child(self, child):self.children.append(child)# 创建文件系统结构 root FileNode("roo…...

C++学习/复习5--构造函数与初始化/static成员/友元/内部类/匿名对象/编译器的拷贝构造优化
一、本章概要 二、再谈构造函数 1.构造体赋初值与初始化 2.初始化列表与初始化 2.1定义 2.2注意事项与举例 3.explicit关键字与构造函数 3.1隐式类型转换 也叫做自动类型转换 这种转换通常是从存储范围小的类型到存储范围大的类型,或者是从低精度的数值类型到高…...

数学建模--LaTeX基本介绍和入门
1.引言 (1)上次我们介绍到了我们这个团队第一次参加这个数学建模比赛,就是这个电工杯,我是一名论文手,我们在这个下午也是对于这个比赛过程中出现的问题做了相应的分析,每个人也是进行了反思,知…...

【Java面试】二、Redis篇(中)
文章目录 1、Redis持久化1.1 RDB1.2 AOF1.3 RDB与AOF的对比 2、数据过期策略(删除策略)2.1 惰性删除2.2 定期删除 3、数据淘汰策略4、主从复制4.1 主从全量同步4.2 增量同步 5、哨兵模式5.1 服务状态监控5.2 哨兵选主规则5.3 哨兵模式下,Redi…...
v1.30.1)
二进制安装Kubernetes(k8s)v1.30.1
二进制安装Kubernetes(k8s)v1.30.1 https://github.com/cby-chen/Kubernetes 开源不易,帮忙点个star,谢谢了 介绍 kubernetes(k8s)二进制高可用安装部署,支持IPv4IPv6双栈。 我使用IPV6的目的是…...
俄罗斯半导体领域迈出坚实步伐:首台光刻机诞生,目标直指7纳米工艺
近日,国外媒体纷纷报道,俄罗斯在半导体技术领域取得了重要突破,首台光刻机已经制造完成并正在进行严格的测试阶段。这一里程碑式的事件标志着俄罗斯在自主发展半导体技术的道路上迈出了坚实的一步。 据俄罗斯联邦工业和贸易部副部长瓦西里-什…...

什么是容器:从基础到进阶的全面介绍
✨✨ 欢迎大家来访Srlua的博文(づ ̄3 ̄)づ╭❤~✨✨ 🌟🌟 欢迎各位亲爱的读者,感谢你们抽出宝贵的时间来阅读我的文章。 我是Srlua小谢,在这里我会分享我的知识和经验。&am…...

力扣 第 399 场周赛 解题报告 | 珂学家 | 调和级数 + 分块DP
前言 T1. 优质数对的总数 I 题型: 签到 class Solution:def numberOfPairs(self, nums1: List[int], nums2: List[int], k: int) -> int:res 0for v1 in nums1:for v2 in nums2:if v1 % (v2 * k) 0:res 1return resT2. 压缩字符串 III 思路: 模拟 感觉引入一个栈&…...
Redis的下载、安装、启动和初尝试【超级简单】
redis最好是在Linux系统中使用,这是最接近生产实际的环境。 不过,我们初学者,目的是学习Redis的使用、原理,如果在Linux下直接学习Redis,很可能会因为命令不熟悉而劝退,这是不好的。 因此,我主张…...
v-cloak 用于在 Vue 实例渲染完成之前隐藏绑定的元素
如果你是后端开发者(php),在接触一些vue2开发的后台时,会发现有这段代码: # CDN <script src"https://cdn.jsdelivr.net/npm/vue2/dist/vue.js"></script> # 或 <script src"https://cd…...

港股:并不意外的获利了结
中金公司表示,风险偏好驱动的反弹已经较为充分,分歧和获利了结也不意外。接下来或在当前水平震荡盘整,等待更多催化剂。 在持续一个月的大涨后,港股市场上周出现明显回调。此前我们多次提示,市场已经超买,情…...
)
Python项目开发实战:工厂库存管理系统(案例教程)
一、项目背景与意义 随着制造业的快速发展,工厂库存管理成为了企业运营中不可或缺的一部分。一个高效的库存管理系统能够确保物料供应的及时性、降低库存成本、提高生产效率。因此,我们决定使用Python开发一个工厂库存管理系统,以满足工厂日常库存管理的需求。 二、系统需求…...

VS2022 嘿嘿
还是大二的时候就开始用这个,但居然是为了用PB,-_-|| 用了段时间换成了C#,依稀还记得大佬们纠正我的读法,别读C井,应该读C夏普。。。 安装过程其实也没啥,就是关键Key得花时间找,我好不容易搞…...

Flutter 中的 PhysicalShape 小部件:全面指南
Flutter 中的 PhysicalShape 小部件:全面指南 在Flutter中,PhysicalShape小部件是一个能够为子组件添加物理效果的边框和阴影的装饰性小部件。它能够模拟真实世界中物体的立体感,通过在子组件的周围创建一个可自定义的形状,并添加…...

CAD二次开发(6)-用户交互之选择集
1. 简单测试 测试让选中的图形描红 [CommandMethod("SeleDemo")]public void SeleDemo(){Database db HostApplicationServices.WorkingDatabase;Editor ed Application.DocumentManager.MdiActiveDocument.Editor;PromptSelectionResult psr ed.GetSelection();…...

如何使用性能监控工具分析JVM性能瓶颈
1、jConsole: jConsole是JDK自带的Java监控和管理控制台。它提供了一个图形用户界面(GUI),用于监控和管理Java应用程序的性能和资源消耗。 使用方法:打开jdk\bin\jconsole.exe,连接到正在运行的Java进程&a…...
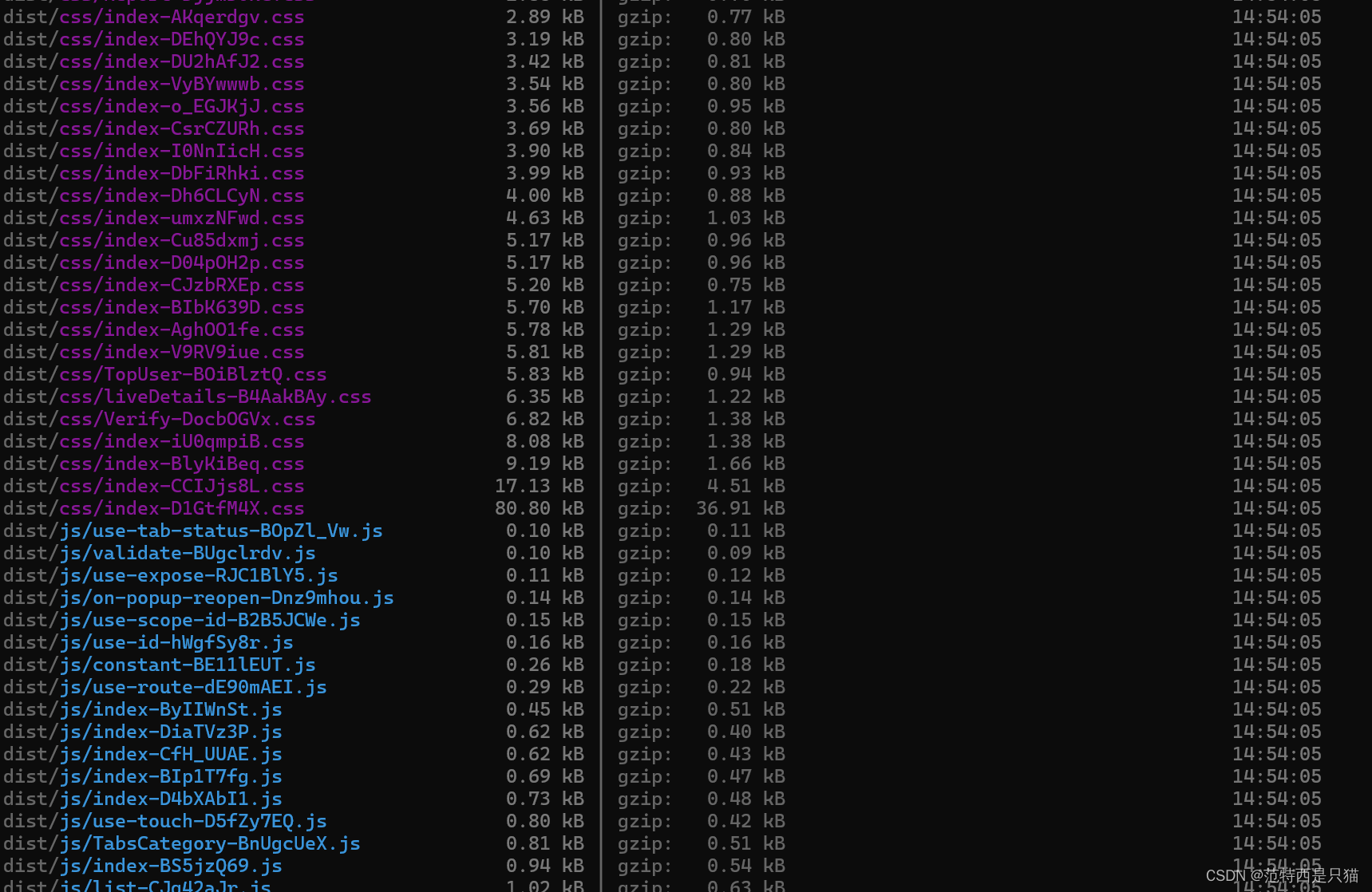
解决vite打包只生成了一个css和js文件问题
文章目录 1. 打包遇到的问题2. 问题原因及修改3. 调整后再次打包🆗 1. 打包遇到的问题 今天整了一个项目,试了下打包,发下打包后只生成了一个css文件,和一个js文件, 这样肯定是不行的,因为这样这个文件的包…...

数据访问层设计_4.灵活运用XML Schema
1.XML Schema XML Schema用来描述XML文档合法结构、内容和限制。XML Schema由XML1.0自描述,并且使用了命名空间,有丰富的内嵌数据类型及其强大的数据结构定义功能,充分地改造了并且极大地扩展了DTDs(传统描述XML文档结构和内容限…...
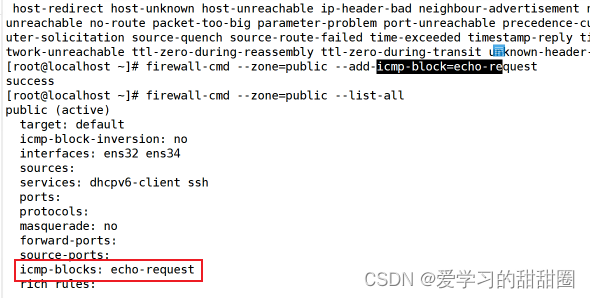
【Linux安全】Firewalld防火墙基础
目录 一、Firewalld概述 二、Firewalld和iptables的关系 三、Firewalld网络区域 1、firewalld防火墙预定义了9个区域: 2、firewalld 数据包处理原则 3、firewalld数据处理流程 4、firewalld检查数据包的源地址的规则 四、Firewalld防火墙的配置方法 1、firewalld 命令…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...
