【三维重建】ePnP
PnP问题应用与一下场景:
已知三维点和对应二维点以及相机相机内参数,可以获取相机外参。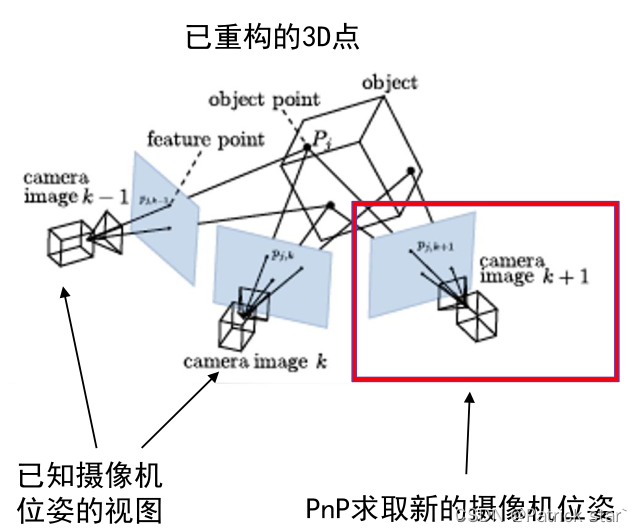
我们介绍其中的一种算法:ePnP
算法流程
1、ePnP算法首先在世界坐标系内寻找4个控制点,记作 C 1 w , C 2 w , C 3 w , C 4 w C_1^w,C_2^w,C_3^w,C_4^w C1w,C2w,C3w,C4w,使得:
对于世界坐标系内任意一点 P 1 w , P_1^w, P1w,存在对应的 α i = [ α i 1 , α i 2 , α i 3 , α i 4 ] T \alpha_i=[\alpha_{i1},\alpha_{i2},\alpha_{i3},\alpha_{i4}]^T αi=[αi1,αi2,αi3,αi4]T,满足:
P i w = ∑ j = 1 4 α i j C j w , w i t h ∑ j = 1 4 α i j = 1 P_i^w = \sum_{j=1}^4\alpha_{ij}C_j^w, {\kern 20pt} with\sum_{j=1}^4\alpha_{ij}=1 Piw=j=1∑4αijCjw,withj=1∑4αij=1
世界坐标系上的 P w P^w Pw 经过 R , t R,t R,t 变换可以得到相机坐标系下的点 P c P^c Pc :
P i c = R P i w + t = R ( ∑ j = 1 4 α i j C j w ) + t P_i^c = RP_i^w+t=R\left(\sum_{j=1}^4\alpha_{ij}C_j^w\right) + t Pic=RPiw+t=R(j=1∑4αijCjw)+t
由于 ∑ j = 1 4 α i j = 1 \sum_{j=1}^4\alpha_{ij}=1 ∑j=14αij=1,因此 t = ∑ j = 1 4 α i j t t=\sum_{j=1}^4\alpha_{ij}t t=∑j=14αijt 带入上式得 ( C j w 是世界坐标系下的控制点, C j c 是世界坐标系下的控制点 ) (C_j^w是世界坐标系下的控制点,C_j^c是世界坐标系下的控制点) (Cjw是世界坐标系下的控制点,Cjc是世界坐标系下的控制点):
P i c = ∑ j − 1 4 α i j ( R C j w + t ) = ∑ j − 1 4 α i j C j c , ( C j c = R C j w + t ) P_i^c = \sum_{j-1}^4\alpha_{ij}(RC_j^w + t)= \sum_{j-1}^4\alpha_{ij}C_j^c,{\color{red} \left(C_j^c = RC_j^w+t \right)} Pic=j−1∑4αij(RCjw+t)=j−1∑4αijCjc,(Cjc=RCjw+t)
通过内参矩阵,建立相机坐标系下的点 P c P^c Pc 到像素坐标系下的点 p p p 的映射:
p i = s i [ u i v i 1 ] = K P i c = [ f u 0 u c 0 f v v c 0 0 1 ] ∑ j = 1 4 α i j [ C x j c C y j c C z j c ] p_i = s_i\begin{bmatrix}u_i \\ v_i \\ 1 \end{bmatrix} = KP^c_i=\begin{bmatrix}f_u &0 & u_c \\0& f_v & v_c \\ 0&0&1 \end{bmatrix}\sum_{j=1}^4\alpha_{ij}\begin{bmatrix}C_{xj}^c \\C_{yj}^c \\ C_{zj}^c \end{bmatrix} pi=si uivi1 =KPic= fu000fv0ucvc1 j=1∑4αij CxjcCyjcCzjc
将公式展开,可得:
∑ j = 1 4 α i j f u C x j c + α i j ( u c − u i ) C z j c = 0 ∑ j = 1 4 α i j f v C y j c + α i j ( v c − v i ) C z j c = 0 \sum_{j=1}^4\alpha_{ij}f_uC^c_{xj} + \alpha_{ij}(u_c-u_i)C_{zj}^c = 0 \\ \sum_{j=1}^4\alpha_{ij}f_vC^c_{yj} + \alpha_{ij}(v_c-v_i)C_{zj}^c = 0 j=1∑4αijfuCxjc+αij(uc−ui)Czjc=0j=1∑4αijfvCyjc+αij(vc−vi)Czjc=0
对于上述公式 只有相机坐标系下的四个控制点 C j c C_j^c Cjc 未知,每个控制点有三个参数,因此一共有12个未知数。每对点能建立两个方程组,所以,至少要6对点才能进行求解。
f u [ α i 1 α i 2 α i 3 α i 4 ] [ C x 1 c C x 2 c C x 3 c C x 4 c ] + ( u c − u i ) [ α i 1 α i 2 α i 3 α i 4 ] [ C z 1 c C z 2 c C z 3 c C z 4 c ] = 0 f v [ α i 1 α i 2 α i 3 α i 4 ] [ C y 1 c C y 2 c C y 3 c C y 4 c ] + ( v c − v i ) [ α i 1 α i 2 α i 3 α i 4 ] [ C z 1 c C z 2 c C z 3 c C z 4 c ] = 0 [ f u α i 1 f u α i 2 f u α i 3 f u α i 4 0 0 0 0 ( u c − u i ) α i 1 ( u c − u i ) α i 2 ( u c − u i ) α i 3 ( u c − u i ) α i 4 0 0 0 0 f v α i 1 f v α i 2 f v α i 3 f v α i 4 ( v c − v i ) α i 1 ( v c − v i ) α i 2 ( v c − v i ) α i 3 ( v c − v i ) α i 4 ] [ C x 1 c C x 2 c C x 3 c C x 4 c C y 1 c C y 2 c C y 3 c C y 4 c C z 1 c C z 2 c C z 3 c C z 4 c ] = 0 f_u \begin{bmatrix} \alpha_{i1} & \alpha_{i2} & \alpha_{i3} & \alpha_{i4} \end{bmatrix}\begin{bmatrix} C_{x1}^c \\ C_{x2}^c \\ C_{x3}^c \\ C_{x4}^c\end{bmatrix} + (u_c-u_i) \begin{bmatrix} \alpha_{i1} & \alpha_{i2} & \alpha_{i3} & \alpha_{i4} \end{bmatrix} \begin{bmatrix} C_{z1}^c \\ C_{z2}^c \\ C_{z3}^c \\ C_{z4}^c\end{bmatrix} =0 \\ f_v \begin{bmatrix} \alpha_{i1} & \alpha_{i2} & \alpha_{i3} & \alpha_{i4} \end{bmatrix}\begin{bmatrix} C_{y1}^c \\ C_{y2}^c \\ C_{y3}^c \\ C_{y4}^c\end{bmatrix} + (v_c-v_i) \begin{bmatrix} \alpha_{i1} & \alpha_{i2} & \alpha_{i3} & \alpha_{i4} \end{bmatrix} \begin{bmatrix} C_{z1}^c \\ C_{z2}^c \\ C_{z3}^c \\ C_{z4}^c\end{bmatrix} =0 \\\\\\ \begin{bmatrix} f_u\alpha_{i1} & f_u\alpha_{i2} & f_u\alpha_{i3} & f_u\alpha_{i4} &0&0&0&0&(u_c-u_i) \alpha_{i1} & (u_c-u_i) \alpha_{i2} & (u_c-u_i) \alpha_{i3} & (u_c-u_i) \alpha_{i4} \\0&0&0&0&f_v\alpha_{i1} & f_v\alpha_{i2} & f_v\alpha_{i3} & f_v\alpha_{i4}& (v_c-v_i) \alpha_{i1} & (v_c-v_i) \alpha_{i2} & (v_c-v_i) \alpha_{i3} & (v_c-v_i) \alpha_{i4} \end{bmatrix}\begin{bmatrix}C_{x1}^c \\ C_{x2}^c \\ C_{x3}^c \\ C_{x4}^c\\C_{y1}^c \\ C_{y2}^c \\ C_{y3}^c \\ C_{y4}^c \\ C_{z1}^c \\ C_{z2}^c \\ C_{z3}^c \\ C_{z4}^c\end{bmatrix} =0 fu[αi1αi2αi3αi4] Cx1cCx2cCx3cCx4c +(uc−ui)[αi1αi2αi3αi4] Cz1cCz2cCz3cCz4c =0fv[αi1αi2αi3αi4] Cy1cCy2cCy3cCy4c +(vc−vi)[αi1αi2αi3αi4] Cz1cCz2cCz3cCz4c =0[fuαi10fuαi20fuαi30fuαi400fvαi10fvαi20fvαi30fvαi4(uc−ui)αi1(vc−vi)αi1(uc−ui)αi2(vc−vi)αi2(uc−ui)αi3(vc−vi)αi3(uc−ui)αi4(vc−vi)αi4] Cx1cCx2cCx3cCx4cCy1cCy2cCy3cCy4cCz1cCz2cCz3cCz4c =0
找到相机坐标系下的控制点后,就能够求得相机外参:
C j c = R C j w + t [ C x j c C y j c C z j c ] = [ r 1 r 2 r 3 r 4 r 5 r 6 r 7 r 8 r 9 ] [ C x j w C y j w C z j w ] + [ t 1 t 2 t 3 ] C x j c = r 1 C x j w + r 2 C y j w + r 3 C z j w + t 1 C y j c = r 4 C x j w + r 5 C y j w + r 6 C z j w + t 2 C z j c = r 7 C x j w + r 8 C y j w + r 9 C z j w + t 3 [ C x 1 c C y 1 c C z 1 c C x 2 c C y 2 c C z 2 c C x 3 c C y 3 c C z 3 c C x 4 c C y 4 c C z 4 c ] = [ C x 1 w C y 1 w C z 1 w 0 0 0 0 0 0 1 0 0 0 0 0 C x 1 w C y 1 w C z 1 w 0 0 0 0 1 0 0 0 0 0 0 0 C x 1 w C y 1 w C z 1 w 0 0 1 C x 2 w C y 2 w C z 2 w 0 0 0 0 0 0 1 0 0 0 0 0 C x 2 w C y 2 w C z 2 w 0 0 0 0 1 0 0 0 0 0 0 0 C x 2 w C y 2 w C z 2 w 0 0 1 C x 3 w C y 3 w C z 3 w 0 0 0 0 0 0 1 0 0 0 0 0 C x 3 w C y 3 w C z 3 w 0 0 0 0 1 0 0 0 0 0 0 0 C x 3 w C y 3 w C z 3 w 0 0 1 C x 4 w C y 4 w C z 4 w 0 0 0 0 0 0 1 0 0 0 0 0 C x 4 w C y 4 w C z 4 w 0 0 0 0 1 0 0 0 0 0 0 0 C x 4 w C y 4 w C z 4 w 0 0 1 ] [ r 1 r 2 r 3 r 4 r 5 r 6 r 7 r 8 r 9 t 1 t 2 t 3 ] \begin{aligned} &C_j^c = RC_j^w+t\\\\ &\begin{bmatrix}C_{xj}^c \\ C_{yj}^c \\ C_{zj}^c \end{bmatrix} = \begin{bmatrix} r_1 & r_2 & r_3 \\ r_4 & r_5 & r_6 \\r_7 & r_8 & r_9 \end{bmatrix}\begin{bmatrix}C_{xj}^w \\ C_{yj}^w \\ C_{zj}^w \end{bmatrix} + \begin{bmatrix} t_1 \\ t_2 \\ t_3\end{bmatrix} \\\\ &C_{xj}^c = r_1C_{xj}^w + r_2C_{yj}^w + r_3C_{zj}^w + t_1\\ &C_{yj}^c = r_4C_{xj}^w + r_5C_{yj}^w + r_6C_{zj}^w + t_2\\ &C_{zj}^c = r_7C_{xj}^w + r_8C_{yj}^w + r_9C_{zj}^w + t_3\\ \\\\ &\begin{bmatrix}C_{x1}^c \\ C_{y1}^c \\C_{z1}^c \\C_{x2}^c \\ C_{y2}^c \\C_{z2}^c \\C_{x3}^c \\ C_{y3}^c \\C_{z3}^c \\C_{x4}^c \\ C_{y4}^c \\C_{z4}^c\end{bmatrix} = \begin{bmatrix} C_{x1}^w & C_{y1}^w & C_{z1}^w&0&0&0&0&0&0&1&0&0 \\ 0&0&0&C_{x1}^w & C_{y1}^w & C_{z1}^w &0&0&0&0&1&0\\ 0&0&0&0&0&0& C_{x1}^w & C_{y1}^w & C_{z1}^w &0&0&1\\ C_{x2}^w & C_{y2}^w & C_{z2}^w&0&0&0&0&0&0&1&0&0 \\ 0&0&0&C_{x2}^w & C_{y2}^w & C_{z2}^w &0&0&0&0&1&0\\ 0&0&0&0&0&0& C_{x2}^w & C_{y2}^w & C_{z2}^w &0&0&1 \\ C_{x3}^w & C_{y3}^w & C_{z3}^w&0&0&0&0&0&0&1&0&0 \\ 0&0&0&C_{x3}^w & C_{y3}^w & C_{z3}^w &0&0&0&0&1&0\\ 0&0&0&0&0&0& C_{x3}^w & C_{y3}^w & C_{z3}^w &0&0&1\\ C_{x4}^w & C_{y4}^w & C_{z4}^w&0&0&0&0&0&0&1&0&0 \\ 0&0&0&C_{x4}^w & C_{y4}^w & C_{z4}^w &0&0&0&0&1&0\\ 0&0&0&0&0&0& C_{x4}^w & C_{y4}^w & C_{z4}^w &0&0&1 \end{bmatrix} \begin{bmatrix}r_1 \\ r_2 \\ r_3 \\ r_4 \\ r_5 \\ r_6 \\ r_7 \\ r_8 \\ r_9 \\t_1\\t_2\\t_3 \end{bmatrix} \end{aligned} Cjc=RCjw+t CxjcCyjcCzjc = r1r4r7r2r5r8r3r6r9 CxjwCyjwCzjw + t1t2t3 Cxjc=r1Cxjw+r2Cyjw+r3Czjw+t1Cyjc=r4Cxjw+r5Cyjw+r6Czjw+t2Czjc=r7Cxjw+r8Cyjw+r9Czjw+t3 Cx1cCy1cCz1cCx2cCy2cCz2cCx3cCy3cCz3cCx4cCy4cCz4c = Cx1w00Cx2w00Cx3w00Cx4w00Cy1w00Cy2w00Cy3w00Cy4w00Cz1w00Cz2w00Cz3w00Cz4w000Cx1w00Cx2w00Cx3w00Cx4w00Cy1w00Cy2w00Cy3w00Cy4w00Cz1w00Cz2w00Cz3w00Cz4w000Cx1w00Cx2w00Cx3w00Cx4w00Cy1w00Cy2w00Cy3w00Cy4w00Cz1w00Cz2w00Cz3w00Cz4w100100100100010010010010001001001001 r1r2r3r4r5r6r7r8r9t1t2t3
控制点选取
原则上,就是只要选择3个线性无关的点,就可以表示任意一个三维点,但由于方程组是4,如何是3个控制点只能求得最小二乘解。论文中给出了具体的选择方法。 3D参考点集为 { P i w , i = 1 , ⋯ , n } \left\{P^w_i,i=1,\cdots,n \right \} {Piw,i=1,⋯,n}, 选择3D点的中心为第一个控制点:
C 1 w = 1 n ∑ i = 1 n P i w C^w_1=\frac{1}{n}\sum_{i=1}^nP^w_i C1w=n1i=1∑nPiw
进而得到矩阵:
A = [ ( P 1 w ) T − ( C 1 w ) T ⋯ ( P n w ) T − ( C n w ) T ] A=\begin{bmatrix}{(P_{1}^{w})}^{T} - {(C_{1}^{w})}^{T} \\ \cdots \\ {(P_{n}^{w})}^{T} - {(C_{n}^{w})}^{T} \end{bmatrix} A= (P1w)T−(C1w)T⋯(Pnw)T−(Cnw)T
记 A T A A^TA ATA的特征值为 λ i \lambda_i λi, 特征向量为 V i V_i Vi ,那么剩下的三个点为:
C w = C 1 w + λ i 1 2 V i , i = 1 , 2 , 3 C^w = C_1^w +\lambda^{\frac{1}{2}}_iV_i,\ i = 1,2,3 Cw=C1w+λi21Vi, i=1,2,3
求解 α \alpha α
联立方程组:
P i w = α i 1 C 1 w + α i 2 C 2 w + α i 3 C 3 w + α i 4 C 4 w [ x i y i z i ] = α i 1 [ C x 1 w C y 1 w C z 1 w ] + α i 2 [ C x 2 w C y 2 w C z 2 w ] + α i 3 [ C x 3 w C y 3 w C z 3 w ] + α i 4 [ C x 4 w C y 4 w C z 4 w ] \begin{aligned} &P_i^w = \alpha_{i1}C_1^w+\alpha_{i2}C_2^w+\alpha_{i3}C_3^w+\alpha_{i4}C_4^w \\\\ &\begin{bmatrix} x_i \\y_i\\z_i\end{bmatrix} = \alpha_{i1}\begin{bmatrix} C_{x1}^w \\C_{y1}^w\\C_{z1}^w\end{bmatrix}+\alpha_{i2}\begin{bmatrix} C_{x2}^w \\C_{y2}^w\\C_{z2}^w\end{bmatrix}+\alpha_{i3}\begin{bmatrix} C_{x3}^w \\C_{y3}^w\\C_{z3}^w\end{bmatrix}+\alpha_{i4}\begin{bmatrix} C_{x4}^w \\C_{y4}^w\\C_{z4}^w\end{bmatrix} \end{aligned} Piw=αi1C1w+αi2C2w+αi3C3w+αi4C4w xiyizi =αi1 Cx1wCy1wCz1w +αi2 Cx2wCy2wCz2w +αi3 Cx3wCy3wCz3w +αi4 Cx4wCy4wCz4w
每个点可以得到4个方程组:
x i = α i 1 C x 1 w + α i 2 C x 2 w + α i 3 C x 3 w + α i 4 C x 4 w y i = α i 1 C y 1 w + α i 2 C y 2 w + α i 3 C y 3 w + α i 4 C y 4 w z i = α i 1 C z 1 w + α i 2 C z 2 w + α i 3 C z 3 w + α i 4 C z 4 w 1 = α i 1 + α i 2 + α i 3 + α i 4 x_i=\alpha_{i1}C_{x1}^w+\alpha_{i2}C_{x2}^w+\alpha_{i3}C_{x3}^w+\alpha_{i4}C_{x4}^w\\ y_i=\alpha_{i1}C_{y1}^w+\alpha_{i2}C_{y2}^w+\alpha_{i3}C_{y3}^w+\alpha_{i4}C_{y4}^w\\ z_i=\alpha_{i1}C_{z1}^w+\alpha_{i2}C_{z2}^w+\alpha_{i3}C_{z3}^w+\alpha_{i4}C_{z4}^w\\ 1= \alpha_{i1}+\alpha_{i2}+\alpha_{i3}+\alpha_{i4} xi=αi1Cx1w+αi2Cx2w+αi3Cx3w+αi4Cx4wyi=αi1Cy1w+αi2Cy2w+αi3Cy3w+αi4Cy4wzi=αi1Cz1w+αi2Cz2w+αi3Cz3w+αi4Cz4w1=αi1+αi2+αi3+αi4
用矩阵的方式可表示为:
[ x i y i z i 1 ] = [ C x 1 w C x 2 w C x 3 w C x 4 w C y 1 w C y 2 w C y 3 w C y 4 w C z 1 w C z 2 w C z 3 w C z 4 w 1 1 1 1 ] [ α i 1 α i 2 α i 3 α i 4 ] ⟶ [ C x 1 w C x 2 w C x 3 w C x 4 w C y 1 w C y 2 w C y 3 w C y 4 w C z 1 w C z 2 w C z 3 w C z 4 w 1 1 1 1 ] − 1 [ x i y i z i 1 ] = [ α i 1 α i 2 α i 3 α i 4 ] \begin{bmatrix} x_i \\ y_i \\ z_i \\ 1 \end{bmatrix} = \begin{bmatrix} C_{x1}^w &C_{x2}^w &C_{x3}^w &C_{x4}^w \\ C_{y1}^w &C_{y2}^w &C_{y3}^w &C_{y4}^w \\ C_{z1}^w &C_{z2}^w &C_{z3}^w &C_{z4}^w \\ 1&1&1&1 \end{bmatrix} \begin{bmatrix} \alpha_{i1} \\ \alpha_{i2} \\ \alpha_{i3} \\ \alpha_{i4}\end{bmatrix} \longrightarrow \begin{bmatrix} C_{x1}^w &C_{x2}^w &C_{x3}^w &C_{x4}^w \\ C_{y1}^w &C_{y2}^w &C_{y3}^w &C_{y4}^w \\ C_{z1}^w &C_{z2}^w &C_{z3}^w &C_{z4}^w \\ 1&1&1&1 \end{bmatrix} ^{-1}\begin{bmatrix} x_i \\ y_i \\ z_i \\ 1 \end{bmatrix} = \begin{bmatrix} \alpha_{i1} \\ \alpha_{i2} \\ \alpha_{i3} \\ \alpha_{i4}\end{bmatrix} xiyizi1 = Cx1wCy1wCz1w1Cx2wCy2wCz2w1Cx3wCy3wCz3w1Cx4wCy4wCz4w1 αi1αi2αi3αi4 ⟶ Cx1wCy1wCz1w1Cx2wCy2wCz2w1Cx3wCy3wCz3w1Cx4wCy4wCz4w1 −1 xiyizi1 = αi1αi2αi3αi4
void Rebuild::ePnP(const std::vector<Eigen::Vector3d> &p3ds, const std::vector<Eigen::Vector2d> &p2ds, Camera &camera) {auto blog = _blog;blog->write("ePnP:");/**寻找4个控制点**///求取重心Eigen::Vector3d center = Eigen::Vector3d::Zero();std::vector<Eigen::Vector3d> control_points_w(4);for (int i = 0; i < p3ds.size(); i++) {center(0) += p3ds[i](0);center(1) += p3ds[i](1);center(2) += p3ds[i](2);}center(0) /= p3ds.size();center(1) /= p3ds.size();center(2) /= p3ds.size();control_points_w[0] = center;blog->write("center:");blog->write(center);blog->write("");//构建矩阵Eigen::MatrixXd A = Eigen::MatrixXd::Zero(p3ds.size(), 3);for (int i = 0; i < p3ds.size(); i++) {A(i, 0) = p3ds[i](0) - center(0);A(i, 1) = p3ds[i](1) - center(1);A(i, 2) = p3ds[i](2) - center(2);}Eigen::MatrixXd M = A.transpose() * A;Eigen::EigenSolver<Eigen::MatrixXd> solver(M);Eigen::VectorXd eigenValues = solver.eigenvalues().real();Eigen::MatrixXd eigenVectors = solver.eigenvectors().real();blog->write("eigenValues:");blog->write(eigenValues);blog->write("");blog->write("eigenVectors:");blog->write(eigenVectors);blog->write("");for (int i = 1; i < 4; i++) {control_points_w[i] = control_points_w[0] + sqrt(eigenValues(i - 1)) * eigenVectors.col(i - 1);}blog->write("control_points_w:");for (int i = 0; i < 4; i++) {blog->write(control_points_w[i]);}blog->write("");/**求解alpha**/Eigen::MatrixXd C_w = Eigen::MatrixXd::Zero(4, 4);for (int i = 0; i < 4; i++) {double x = control_points_w[i](0);double y = control_points_w[i](1);double z = control_points_w[i](2);C_w(0, i) = x;C_w(1, i) = y;C_w(2, i) = z;C_w(3, i) = 1;}Eigen::MatrixXd C_w_inv = C_w.inverse();blog->write("C_w:");blog->write(C_w);blog->write("");blog->write("C_w_inv:");blog->write(C_w_inv);blog->write("");double fu = camera._K(0, 0);double fv = camera._K(1, 1);double uc = camera._K(0, 2);double vc = camera._K(1, 2);Eigen::MatrixXd D =Eigen::MatrixXd::Zero(int(2 * p3ds.size()), 12);for (int i = 0; i < p3ds.size(); i++) {Eigen::Vector3d p3d = p3ds[i];Eigen::Vector2d p2d = p2ds[i];Eigen::Vector4d b;b << p3d(0), p3d(1), p3d(2), 1;Eigen::Vector4d alpha = C_w_inv * b;D(i * 2, 0) = fu * alpha(0);D(i * 2, 1) = fu * alpha(1);D(i * 2, 2) = fu * alpha(2);D(i * 2, 3) = fu * alpha(3);D(i * 2, 8) = (uc - p2d(0)) * alpha(0);D(i * 2, 9) = (uc - p2d(0)) * alpha(1);D(i * 2, 10) = (uc - p2d(0)) * alpha(2);D(i * 2, 11) = (uc - p2d(0)) * alpha(3);D(i * 2 + 1, 4) = fv * alpha(0);D(i * 2 + 1, 5) = fv * alpha(1);D(i * 2 + 1, 6) = fv * alpha(2);D(i * 2 + 1, 7) = fv * alpha(3);D(i * 2 + 1, 8) = (vc - p2d(1)) * alpha(0);D(i * 2 + 1, 9) = (vc - p2d(1)) * alpha(1);D(i * 2 + 1, 10) = (vc - p2d(1)) * alpha(2);D(i * 2 + 1, 11) = (vc - p2d(1)) * alpha(3);if(i == 0){blog->write("alpha:");blog->write(alpha);blog->write("");}}blog->write("D:");blog->write(D);blog->write("");Eigen::JacobiSVD<Eigen::MatrixXd> svd(D, Eigen::ComputeFullV | Eigen::ComputeFullU);auto V = svd.matrixV();std::vector<Eigen::Vector3d> control_points_c(4);blog->write("control_points_c:");for (int i = 0; i < 4; i++) {double x = V(i);double y = V(i + 4);double z = V(i + 8);Eigen::Vector3d p3d(x, y, z);control_points_c[i] = p3d;blog->write(p3d);}blog->write("");Eigen::MatrixXd Q = Eigen::MatrixXd::Zero(12, 12);Eigen::VectorXd C_c = Eigen::VectorXd::Zero(12);for (int i = 0; i < 4; i++) {C_c(i * 3) = control_points_c[i](0);C_c(i * 3 + 1) = control_points_c[i](1);C_c(i * 3 + 2) = control_points_c[i](2);Q(i * 3, 0) = control_points_w[i](0);Q(i * 3, 1) = control_points_w[i](1);Q(i * 3, 2) = control_points_w[i](2);Q(i * 3, 9) = 1;Q(i * 3 + 1, 3) = control_points_w[i](0);Q(i * 3 + 1, 4) = control_points_w[i](1);Q(i * 3 + 1, 5) = control_points_w[i](2);Q(i * 3 + 1, 10) = 1;Q(i * 3 + 2, 6) = control_points_w[i](0);Q(i * 3 + 2, 7) = control_points_w[i](1);Q(i * 3 + 2, 8) = control_points_w[i](2);Q(i * 3 + 2, 11) = 1;}blog->write("Q:");blog->write(Q);blog->write("");blog->write("C_c:");blog->write(C_c);blog->write("");Eigen::MatrixXd Q_inv = Q.inverse();blog->write("Q_inv:");blog->write(Q_inv);blog->write("");Eigen::VectorXd ans = Eigen::VectorXd::Zero(12);ans = Q_inv * C_c;blog->write("ans:");blog->write(ans);blog->write("");camera._R(0, 0) = ans(0);camera._R(0, 1) = ans(1);camera._R(0, 2) = ans(2);camera._R(1, 0) = ans(3);camera._R(1, 1) = ans(4);camera._R(1, 2) = ans(5);camera._R(2, 0) = ans(6);camera._R(2, 1) = ans(7);camera._R(2, 2) = ans(8);camera._t(0) = ans(9);camera._t(1) = ans(10);camera._t(2) = ans(11);
}相关文章:

【三维重建】ePnP
PnP问题应用与一下场景: 已知三维点和对应二维点以及相机相机内参数,可以获取相机外参。 我们介绍其中的一种算法:ePnP 算法流程 1、ePnP算法首先在世界坐标系内寻找4个控制点,记作 C 1 w , C 2 w , C 3 w , C 4 w C_1^w,C_2^w,…...

C++进阶之路:何为运算符重载、赋值运算符重载与前后置++重载(类与对象_中篇)
✨✨ 欢迎大家来访Srlua的博文(づ ̄3 ̄)づ╭❤~✨✨ 🌟🌟 欢迎各位亲爱的读者,感谢你们抽出宝贵的时间来阅读我的文章。 我是Srlua小谢,在这里我会分享我的知识和经验。&am…...
8、python基础知识图谱
...

智慧校园建设规划方案
在信息化浪潮的推动下,智慧校园的建设已成为教育现代化的必然趋势。以创新科技赋能教育,打造智慧校园,旨在提升教学品质,优化管理流程,增强学生体验。构建智慧校园需要具有前瞻性的规划方案,它将以教育为核…...

【深度学习实战—8】:基于MediaPipe的人脸检测
✨博客主页:王乐予🎈 ✨年轻人要:Living for the moment(活在当下)!💪 🏆推荐专栏:【图像处理】【千锤百炼Python】【深度学习】【排序算法】 目录 😺一、Med…...

OSCP学习,布置你的Kali Linux
为什么要写这篇文章? 我是一个OSCP学习者,以教促学。同时也能让各位入门的师傅们更好的了解OSCP这门课程。本人文笔不太好,如果有什么写的不对的地方,师傅们多多指正。 参考资料: OSCP 考试电子书 Linux Basics for…...

PWA离线优先策略:提升用户体验的关键步骤
Progressive Web Apps (PWA) 的离线优先策略是通过Service Worker和Cache API实现的,它允许在没有网络连接时仍然可以访问网站的部分或全部内容。 2500G计算机入门到高级架构师开发资料超级大礼包免费送! 1. 创建Service Worker注册文件(se…...
网页提示“非私密连接”是为什么?
网页提示“非私密连接”(英文提示可能是 "Your connection is not private" 或 "Your connection is not secure")主要是因为浏览器无法验证你正试图访问的网站的SSL/TLS证书,或者是证书存在问题,从而无法建立…...

[自动驾驶技术]-8 Tesla自动驾驶方案之硬件(AI Day 2022)
特斯拉在AI Day 2022先介绍了AI编译器,后面又介绍了Dojo的硬件软件,软件部分和AI编译器有部分重叠,本文介绍还是延用AI Day的思路,分为三部分:AI编译和推理,Dojo硬件,Dojo软件。 特斯拉车道检测…...

人力资源管理信息化系统如何支持企业开展管理诊断?
华恒智信人力资源顾问有限公司致力于帮助企业开展人力资源管理方面的各项提升改进工作,在长期的咨询工作中,最常听到企业提到的问题莫过于管理诊断方面的问题,事实上,很多企业在日常工作中,都意识到企业内部存在管理方…...
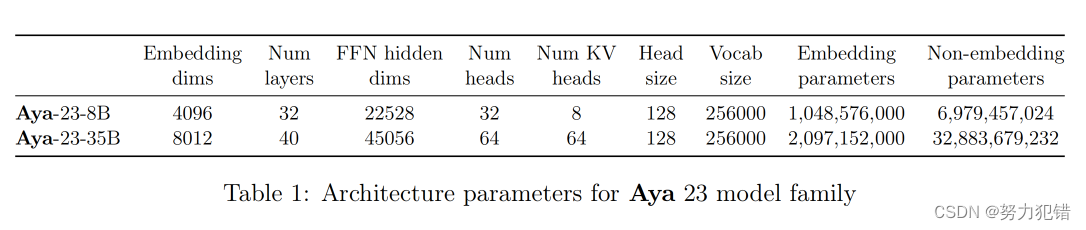
Cohere继Command-R+之后发布大模型Aya-23,性能超越 Gemma、Mistral 等,支持中文
前言 近年来,多语言大模型(MLLM)发展迅速,但大多数模型的性能依然存在显著差距,尤其是在非英语语言方面表现不佳。为了推动多语言自然语言处理技术的发展,Cohere团队发布了新的多语言指令微调模型家族——…...

身为UI设计老鸟,不学点3D,好像要被潮流抛弃啦,卷起来吧。
当前3D原则在UI设计中运用的越来越多,在UI设计中,使用3D元素可以为界面带来以下几个价值: 增强视觉冲击力:3D元素可以通过立体感和逼真的效果,为界面增添视觉冲击力,使得设计更加生动、吸引人,并…...

【C语言】实现贪吃蛇--项目实践(超详细)
前言: 贪吃蛇游戏大家都玩过吧?这次我们要用C语言来亲手制作一个!这个项目不仅能让我们复习C语言的知识,还能了解游戏是怎么一步步做出来的。我们会一起完成蛇的移动、食物的生成,还有碰撞检测等有趣的部分。准备好了…...
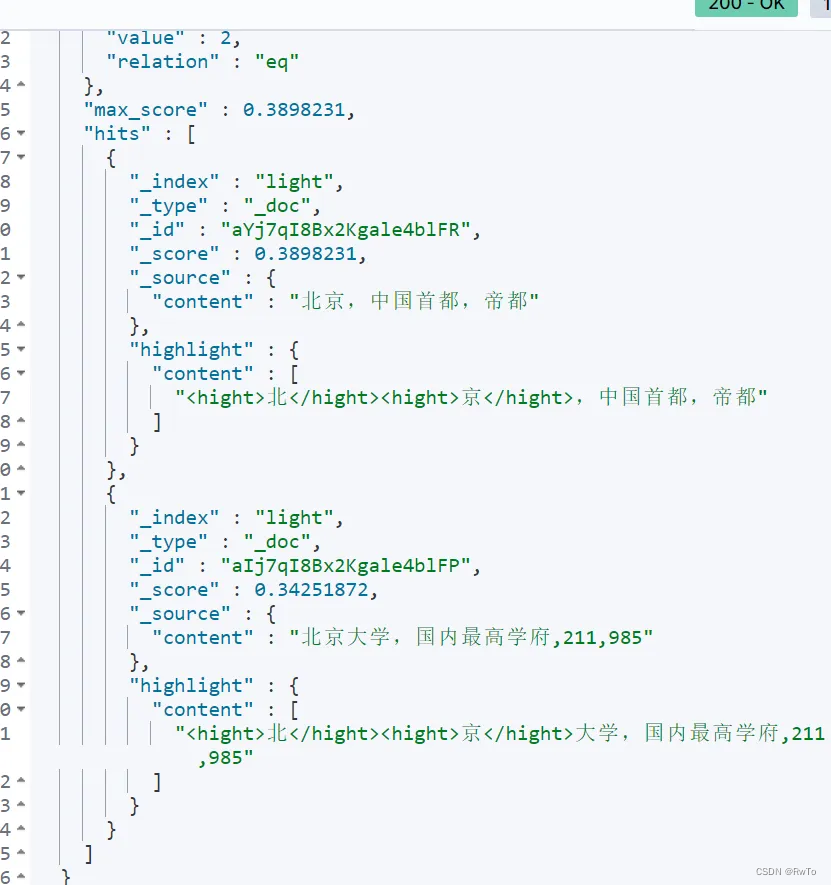
Elasticsearch 分析器的高级用法一(同义词,高亮搜索)
Elasticsearch 分析器的高级用法一(同义词,高亮搜索) 同义词简介分析使用同义词案例 高亮搜索高亮搜索策略unifiedplainvh 同义词 简介 在搜索场景中,同义词用来处理不同的查询词,有可能是想表达相同的搜索目标。 例…...
Python 开心消消乐
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「stormsha的主页」…...

mysql - 索引基本知识梳理
mysql索引基本知识梳理 索引介绍 官方介绍索引是帮助MySQL高效获取数据的数据结构, 原理为以空间换时间, mysql的索引采用的是B树的结构 索引的优缺点 优点: 提高查询效率降低数据库IO成本通过索引对数据进行排序, 降低排序成本, 降低CPU消耗 缺点:…...

Nginx SSL/TLS配置:搭建安全的HTTPS网站
随着互联网安全性的日益提升,HTTPS已经成为网站安全通信的标配。Nginx作为一款高性能的HTTP和反向代理服务器,支持SSL/TLS协议,使得我们可以轻松地搭建安全的HTTPS网站。下面,我们将详细介绍如何在Nginx上配置SSL/TLS,…...

echarts 折线图流光效果偏移或不显示
x轴数据需要字符串数组...
Redis数据类型(上篇)
前提:(key代表键) Redis常用的命令 命令作用keys *查看当前库所有的keyexists key判断某个key是否存在type key查看key是什么类型del key 删除指定的keyunlink key非阻塞删除,仅仅将keys从keyspace元数据中删除,真正的…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

