[蓝桥杯 2020 省 A1] 超级胶水
一.题目
题目描述
小明有 n 颗石子,按顺序摆成一排。
他准备用胶水将这些石子粘在一起。
每颗石子有自己的重量,如果将两颗石子粘在一起,将合并成一颗新的石子,重量是这两颗石子的重量之和。
为了保证石子粘贴牢固,粘贴两颗石子所需要的胶水与两颗石子的重量乘积成正比,本题不考虑物理单位,认为所需要的胶水在数值上等于两颗石子重量的乘积。
每次合并,小明只能合并位置相邻的两颗石子,并将合并出的新石子放在原来的位置。
现在,小明想用最少的胶水将所有石子粘在一起,请帮助小明计算最少需要多少胶水。
输入格式
输入的第一行包含一个整数 n,表示初始时的石子数量。
第二行包含 n 个整数 w 1 , w 2 , … , w n w_1,w_2,…,w_n w1,w2,…,wn,依次表示每颗石子的重量。
输出格式
输出一个整数代表答案。
数据范围
1 ≤ N ≤ 1000,
1 ≤ w i w_i wi ≤ 1000
输入样例1
3
3 4 5
输出样例1
47
输入样例2
8
1 5 2 6 3 7 4 8
输出样例2
546
二.解释
看完题目,一眼贪心,想到之前做过的类似题目(合并石头、合并果子等),先找出相邻乘积最小的两项,按要求计算,但是这样只能过 80% 的数据。
直接计算最复杂的是在序列中找最小乘积的两项,
当n = 3,有序列 = {a,b, c};
我们按要求先合并相邻:
合并a,b,则有f1 = (a * b)+ (a + b) * c = (a * b) + (b * c) + (a * c);
合并b,c,则有f2 = (b * c)+ (b + c) * a = (a * b) + (b * c) + (a * c);
合并不相邻:
合并a,c,则有f3 = (a * c)+ (a + c) * b = (a * b) + (b * c) + (a * c);
得f1 = f2 = f3;
当n = k,有序列 = { a 1 , a 2 , … … , a k a_1, a_2, ……, a_k a1,a2,……,ak}:
我们按要求先合并相邻:
一直合并头两项,则有f1 = ( a 1 ∗ a 2 a_1 * a_2 a1∗a2) + ( a 1 + a 2 a_1 + a_2 a1+a2) * a 3 a_3 a3 + ( a 1 + a 2 + a 3 a_1 + a_2 + a_3 a1+a2+a3) * a 4 a_4 a4 + …… + ( a 1 + a 2 + … … + a k − 1 a_1 + a_2 + …… + a_{k - 1} a1+a2+……+ak−1) * a k a_k ak = ( a 1 ∗ a 2 a_1 * a_2 a1∗a2) + ( a 1 ∗ a 3 a_1 * a_3 a1∗a3) + …… + ( a 1 ∗ a k a_1 * a_k a1∗ak) + ( a 2 ∗ a 3 a_2 * a_3 a2∗a3) + …… + ( a k − 1 ∗ a k a_{k - 1} * a_k ak−1∗ak);
合并其他相邻两项结果也是一样的,可以自己列举。
和并不相邻的两项时,则有f2 = ( a 1 ∗ a j a_1 * a_j a1∗aj) + ( a 1 + a i a_1 + a_i a1+ai) * a j a_j aj + ( a 1 + a i + a j a_1 + a_i + a_j a1+ai+aj) * a x a_x ax + …… + ( a 1 + a i + a j + … … + a y a_1 + a_i + a_j + …… + a_y a1+ai+aj+……+ay) * a z a_z az = ( a 1 ∗ a 2 a_1 * a_2 a1∗a2) + ( a 1 ∗ a 3 a_1 * a_3 a1∗a3) + …… + ( a 1 ∗ a k a_1 * a_k a1∗ak) + ( a 2 ∗ a 3 a_2 * a_3 a2∗a3) + …… + ( a k − 1 ∗ a k a_{k - 1} * a_k ak−1∗ak);
的f1 = f2;
因此合并顺序不会有影响结果,我们可以用一个小顶堆来取数据,每次pop顶端两个数,合并之后再加回堆中即可。
第二种方法,从上面的推导结果我们发现,最终结果都是序列中任意两个数相乘再相加,因此我们可以直接算,再 O(N) 的复杂度得出结果。
三.代码
暴力计算:
#include <iostream>
#include <unordered_map>
#include <algorithm>
#include <cstring>
#include <string>
#include <vector>
#include <set>using namespace std;typedef long long int64;
const int MaxN = 1e5 + 10;int64 InN, InK, Res;
vector<int64> Ns;int main()
{cin >> InN;int a;for (int i = 1; i <= InN; i++){scanf("%d", &a);Ns.push_back(a);}while (Ns.size() > 1){int64 x = 0, y = 1, z = Ns[x] * Ns[y];//取出最小乘积的相邻两个数for (int i = 1; i < Ns.size() - 1; i++){if (z > Ns[i] * Ns[i + 1]){z = Ns[i] * Ns[i + 1];x = i, y = i + 1;}}//放到原位置Res += z;Ns[x] = Ns[x] + Ns[y];Ns.erase(Ns.begin() + y);}cout << Res;return 0;
}
堆优化:
#include <iostream>
#include <unordered_map>
#include <algorithm>
#include <cstring>
#include <string>
#include <vector>
#include <queue>
#include <set>using namespace std;typedef long long int64;
const int MaxN = 1e5 + 10;int64 InN, InK, Res;
int64 Ns[MaxN];
priority_queue<int64, vector<int64>, greater<int64>> PQ;int main()
{cin >> InN;int64 a;for (int i = 1; i <= InN; i++){scanf("%lld", &a);PQ.push(a);}//优化部分while (PQ.size() > 1){int64 A = PQ.top();PQ.pop();int64 B = PQ.top();PQ.pop();PQ.push(A + B);Res += A * B;}cout << Res;return 0;
}
第二种解法:
#include <iostream>
#include <unordered_map>
#include <algorithm>
#include <cstring>
#include <string>
#include <vector>
#include <set>using namespace std;typedef long long int64;
const int MaxN = 1e5 + 10;int64 InN, InK, Res;
int64 Ns[MaxN];int main()
{cin >> InN;int64 a;for (int i = 1; i <= InN; i++){scanf("%lld", Ns + i);}int64 S = Ns[1];for (int i = 2; i <= InN; i++){Res += Ns[i] * S; //累加S += Ns[i]; //前i项的和}cout << Res;return 0;
}
相关文章:

[蓝桥杯 2020 省 A1] 超级胶水
一.题目 题目描述 小明有 n 颗石子,按顺序摆成一排。 他准备用胶水将这些石子粘在一起。 每颗石子有自己的重量,如果将两颗石子粘在一起,将合并成一颗新的石子,重量是这两颗石子的重量之和。 为了保证石子粘贴牢固࿰…...

读书笔记分享
1.苏格拉底只在需要的时候才索取,那样便能以最少的物质满足自身的要求。他认为每个人都天生体质脆弱,只有在贫乏的环境中才会锻炼地强壮起来。生活中的大多数人认为,奢华才是幸福的生活。无休止的物质积聚,让人们每天生活在一个内…...
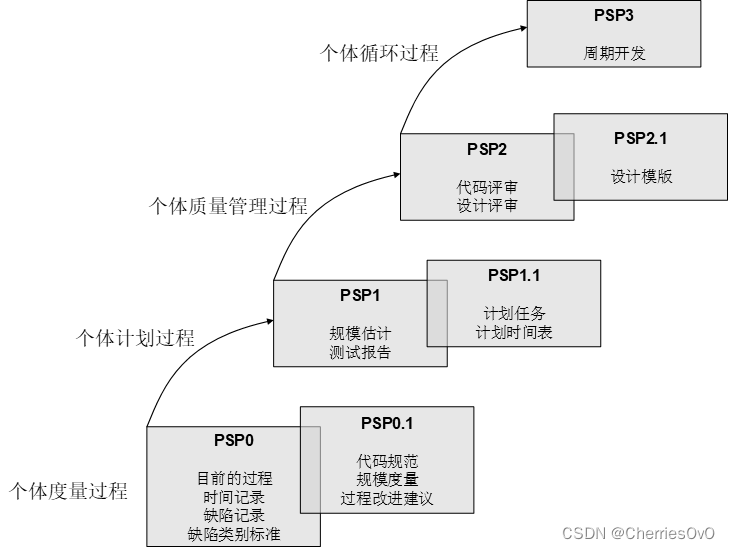
考试宝典——软件过程与管理重点知识总结
概论 软件工程三要素 过程方法工具 软件过程的定义 软件过程是用于软件开发及维护的一系列活动、方法及实践。 常见软件过程分类(五大类) 客户-供应商过程:内部直接影响到客户、外部直接影响开发、向客户交付软件以及软件正确操作与使用的过…...

穿越时空的工厂之旅:探索可视化三维场景的奥秘
在科技日新月异的今天,我们似乎总是在不断追求着更加高效、智能的生产方式。 传统的工厂管理方式往往依赖于平面图纸、纸质文档和现场巡查,这不仅效率低下,而且容易出错。而三维可视化技术通过3D建模和虚拟现实技术,将工厂内部的各…...

2024年推荐的适合电脑和手机操作的线上兼职副业平台
总是会有人在找寻着线上兼职副业,那么在如今的2024年,互联网提供了诸多方便,无论你是宝妈、大学生、程序员、外卖小哥还是打工族,如果你正在寻找副业机会,那么这篇文章将为你提供一些适合电脑和手机操作的线上兼职副业…...

传感器的静态特性
传感器的静态特性是指传感器在稳态(输入量为常量或变化极慢时)输入信号作用下,传感器输出与输入信号之间的关系。这种关系一般用曲线、数学表达式或表格来表示。传感器的静态特性是传感器的基本特性之一,其描述了传感器在不考虑迟…...

如果jupyter notebook不能实现网页自动跳转,参考下面的链接
一招搞定Jupyter-notebook命令行打开之后不能自动跳转浏览器_一招搞定jupter notebook命令行打开之后-CSDN博客...

顺序表实现通讯录项目
目录 一.实现功能: 二.文件结构 三.代码实现 1.初始化 2.通讯录的销毁 3.通讯录添加数据 4.通讯录删除数据 5.通讯录的修改 6.展现通讯录数据 7.通讯录查找 四.代码 SeqList.h Contact.h Contact.c test(通讯录).c 一.实现功能: ⾄少能够存…...
【ai】pycharm设置软件仓库编译运行基于langchain的chatpdf
联想笔记本 y9000p创建python工程: 使用langchain支持openai的向量化embedding安装软件包 发现没有openai ,添加软件仓库打开工具窗口 点击设置...
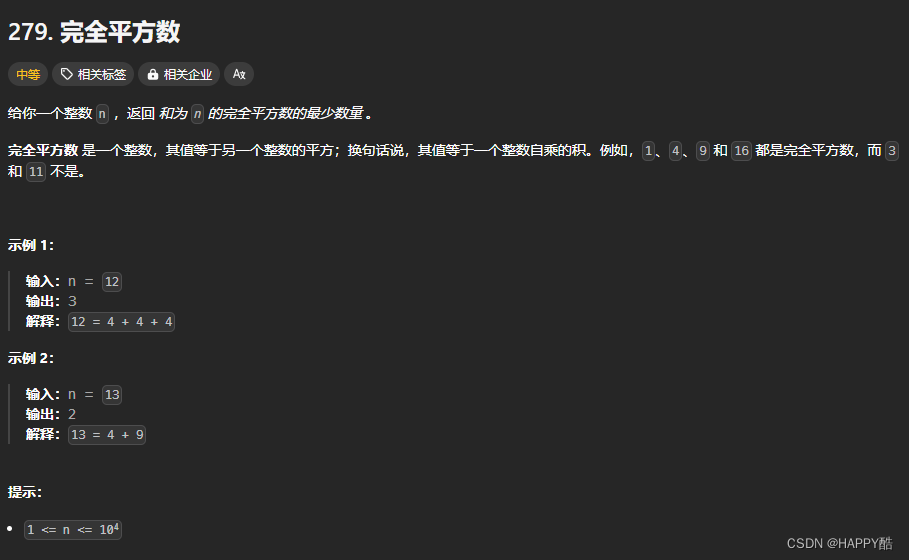
LeetCode:279.完全平方数
class Solution:def numSquares(self, n: int) -> int:dp[i for i in range(n1)]for i in range(2,n1):for j in range(1,int(i**(0.5))1):dp[i]min(dp[i],dp[i-j*j]1)return dp[-1]代码解释 初始化 DP 数组: dp [i for i in range(n1)] 这里,dp[i]…...
相关的面试笔试题(1000加面试笔试题助你轻松捕获大厂Offer))
Python面试宝典:Python中与ORM技术(对象关系映射)相关的面试笔试题(1000加面试笔试题助你轻松捕获大厂Offer)
Python面试宝典:1000加python面试题助你轻松捕获大厂Offer【第二部分:Python高级特性:第十五章:数据库编程:第二节:ORM技术】 第十五章:数据库编程第二节:ORM技术SQLAlchemyDjango ORMORM技术的优势和劣势python中与ORM技术相关的面试笔试题面试题1面试题2面试题3面试题…...

VUE3+TS+elementplus创建table,纯前端的table
一、前言 开始学习前端,直接从VUE3开始,从简单的创建表格开始。因为自己不是专业的程序员,编程主要是为了辅助自己的工作,提高工作效率,VUE的基础知识并不牢固,主要是为了快速上手,能够做出一些…...

UE驻网失败问题(二)
另一个UE注册失败的问题,具体过程如下: 问题现象如上,UE在这个N48上的小区一直在重复上述过程,收到RRC Setup后就不发RRC Setupcomplete,闭上眼睛也知道大概率是这个RRC Setup的配置有问题。 在问题时间点周围查看&…...

【MySQL】第三周作业
【MySQL】第三周作业 1、在数据库example下创建college表。2、在student表上创建视图college_view。3、查看视图college_view的详细结构4、 更新视图。5 、修改视图,6 、删除视图college_view 1、在数据库example下创建college表。 College表内容如下所示 字段名 …...
香橙派 Kunpeng Pro使用教程:从零开始打造个人私密博客
一、引言 在这个日益互联的世界中,单板计算机已经成为创新和个性化解决方案的重要载体。而在单板计算机领域,香橙派 Kunpeng Pro凭借其强大的性能和灵活的应用潜力,正逐渐吸引着全球开发者和技术爱好者的目光。 作为一款集成了华为的鲲鹏处…...

深入探索:中文字符的编码与转移字符的奥秘
新书上架~👇全国包邮奥~ python实用小工具开发教程http://pythontoolsteach.com/3 欢迎关注我👆,收藏下次不迷路┗|`O′|┛ 嗷~~ 目录 一、引言:探索字符编码的世界 二、字符编码基础:理解ASCII与Unicode…...
Ubuntu中 petalinux 安装 移植linux --tftp/tftp-hpa服务的方法
Xilinx 文档 PetaLinux 指南:如何创建 PetaLinux 环境 (2019.1) PetaLinux工具参考指南 PetaLinux安装详解(Xilinx , linux, zynq, zynqMP) petalinux 2020.1安装教程 一、PetaLinux工具和库安装 PetaLinux 工具要求主机系统 /bin/sh 为“b…...

JVM(内存区域划分、类加载机制、垃圾回收机制)
目录 一. 内存区域划分 1.本地方法栈(Native Method Stacks) 2.虚拟机栈(JVM Stacks) 3.程序计数器(Program Counter Register) 4.堆(Heap) 5.元数据区(Metaspace) 二.类加载机制 1.加载 2.验证 3.准备 4.解析 5.初始化 "双亲委派模型" 三. GC 垃圾回收…...
)
C语言---基础内容(万字)
C 语言是一种通用的、面向过程式的计算机程序设计语言。1972 年,为了移植与开发 UNIX 操作系统,丹尼斯里奇在贝尔电话实验室设计开发了 C 语言。 C 语言是一种广泛使用的计算机语言,它与 Java 编程语言一样普及,二者在现代软件程…...

c语言从入门到函数速成(完结篇)
哈喽,小伙伴们大家好呀,本篇文章是这个系列的完结篇,希望大家看完后能有所收获哦 首先能看到这里的同学,一定也是自觉性比较强的了,我会在文章末尾给大家发点小福利 那么,我们先来通过数学中的函数来引入一…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

热烈祝贺埃文科技正式加入可信数据空间发展联盟
2025年4月29日,在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上,可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞,强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...
