图论(四)—最短路问题(Dijkstra)
一、最短路
概念:从某个点 A 到另一个点B的最短距离(或路径)。从点 A 到 B 可能有多条路线,多种距离,求其中最短的距离和相应路径。
最短路径分类:
单源最短路:图中的一个点到其余各点的最短路径
多源最短路:图中任意两点的最短路径
框架图解:

二、朴素Dijkstra算法
算法思想(仅限于非负权重值):从起始点开始,使用贪心的策略,通过加点的方法,每次遍历到起始点距离最近且未被访问过的邻接节点 t ,将 t 加入到集合 S 中,直到访问过所有节点。
通过 N 次循环确定 n 个点到起点的最短路距离
时间复杂度为
1.在没有确定最短路中的所有点(集合 S 以外)找出距离起点最近的点 t
2.对 t 进行标记,加入到集合中
3.用 t 更新其他点的最短路距离
集合 S :已经确定最短路的点(被访问过的点) 定义数组 :从起始点到某点 ( 3 号节点 ) 的最短距离( dis[3] ) 定义二维数组
:
表示从 节点 u 到 节点 v 的距离(区分单向与双向,双向则
) 初始化:
(以节点 1 为起始点) 若 节点 u 与 节点 v 之间没有路径,初始化为
核心代码:
for(int i=1;i<=n;i++)
{int t=-1;for(int j=1;j<=n;j++) // 在没有确定最短路中的所有点找出距离最短的那个点 t if(!s[j] && (t==-1||dis[t]>dis[j]))t=j; s[t]=true; // 代表 t 这个点已经确定最短路了for(int j=1;j<=n;j++) // 用 t 更新其他点的最短距离 dis[j] = min(dis[j],dis[t]+add[t][j]);
}
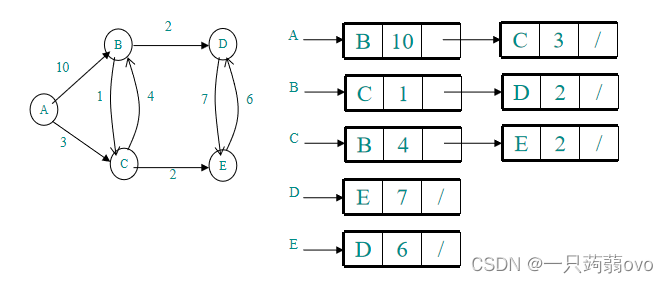
样例解释:对于下图,求出节点 A 的单源最短路






| n | 1 | 2 | 3 | 4 | 5 |
| dis | 0 | 7 | 3 | 9 | 5 |
三、堆优化dijkstra算法
在朴素dijkstra算法中,遍历点是通过for循环对所有节点判断一遍得出的,”对所有节点判断“这一操作消耗了更多的时间。
算法思想:
可以通过堆(优先队列)进行优化,堆(优先队列)存储节点和起始点到该点最短距离,堆(优先队列)按照距离自动排序,取距离最小且未被访问过的点,同通过用邻接链表(或邻接表)储存图的方法,再进行松弛操作,并将进行松弛操作的节点插入堆中。
①.初始化距离:数组dis 都初始化为 0x3f3f3f3f(无穷大),并将 1 号节点插入堆中 (dis[1]=0)
②取出堆顶的点(当前起始点到该点距离最小),判断是否被访问过,不断弹出取堆顶,直至找到未被访问的节点,再根据邻接链表(或邻接表)拓展。
③进行松弛操作,把松弛的点和距离插入到堆中。
堆优化代码:
void dij(int s)
{priority_queue< pair<int,int> > q; // 利用优先队列q.push(make_pair(0,s));memset(dis,127,sizeof(dis));dis[s]=0;while(q.size()){int u=q.top().second;q.pop();if(vis[u]==1) continue;vis[u]=1;for(int i=head[u];i;i=edge[i].next) // 链式前向星{int v=edge[i].to;int w=edge[i].w;if(dis[v]>dis[u]+w){dis[v]=dis[u]+w;q.push(make_pair(-dis[v],v)); // 将路径以负数保存,优先队列默认大根堆}}}
}关于dijkstra算法的正确性证明,参考博文:
Dijkstra贪心算法的准确性证明_为什么这种方法求下来的路径一定是最短?试分析一下它的正确性-CSDN博客
四、dijkstra算法不能用于有负权边的图
通过上述dijkstra思想可以得出,每次松弛操作就是通过当前离起始点最近的点来更新其他点的距离,下面举例说明。
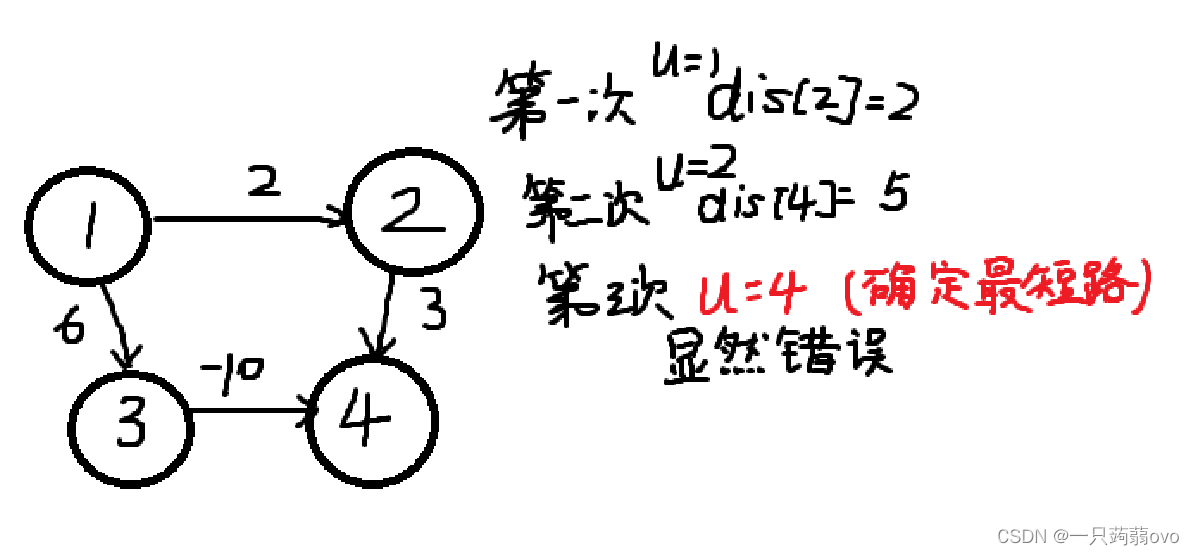
当此时通过 节点 4 更新其他节点, dijkstra 思想已经确定 dis [ 4 ] 为 起始点 到 节点 4 的最短路,显然错误。
相关文章:

图论(四)—最短路问题(Dijkstra)
一、最短路 概念:从某个点 A 到另一个点B的最短距离(或路径)。从点 A 到 B 可能有多条路线,多种距离,求其中最短的距离和相应路径。 最短路径分类: 单源最短路:图中的一个点到其余各点的最短路径…...
用友NC linkVoucher SQL注入漏洞复现
0x01 产品简介 用友NC是由用友公司开发的一套面向大型企业和集团型企业的管理软件产品系列。这一系列产品基于全球最新的互联网技术、云计算技术和移动应用技术,旨在帮助企业创新管理模式、引领商业变革。 0x02 漏洞概述 用友NC /portal/pt/yercommon/linkVoucher 接口存在…...

部署Prometheus + Grafana实现监控数据指标
1.1 Prometheus安装部署 Prometheus监控服务 主机名IP地址系统配置作用Prometheus192.168.110.27/24CentOS 7.94颗CPU 8G内存 100G硬盘Prometheus服务器grafana192.168.110.28/24CentOS 7.94颗CPU 8G内存 100G硬盘grafana服务器 监控机器 主机名IP地址系统配置k8s-master-0…...
GEE27:遥感数据可用数据源计算及条带号制作
1.写在前面 🌍✨今天读了一篇关于遥感数据可用数据源计算及条带号制作的文章,结合着自己的理解,添加了一些内容。 2.GEE代码 📚📚这段代码的主要作用是利用Google Earth Engine平台,通过分析Landsat 8影…...

FURNet问题
1. 为什么选择使用弱监督学习? 弱监督学习减少了对精确标注数据的依赖,这在医学图像处理中尤为重要,因为高质量标注数据通常需要大量专业知识和时间。弱监督学习通过利用少量标注数据或粗略标注数据来训练模型,降低了数据准备的成…...
抖音小店怎么对接达人合作?达人带货的细节分享,附邀约达人话术
大家好,我是电商花花 人有多大胆,地就有多大产,做抖店想要出单,爆单,那必须要对接大量的达人来帮我们带货,抖音小店就是直播电商,帮我们对接的达人越多,出单就越多。 所以做抖店如…...
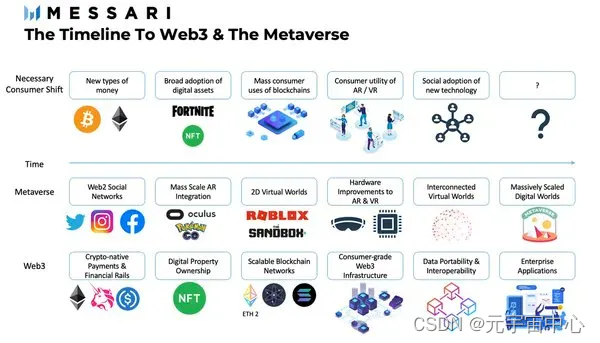
迈向未来:Web3 技术开发的无限可能
在当今的数字时代,互联网技术日新月异,推动着各行各业的变革与发展。从Web1.0的信息发布,到Web2.0的社交互动,互联网的每一次进化都为人们的生活带来了深远的影响。如今,Web3的到来正在开启一个全新的时代,…...
)
Python应用开发——30天学习Streamlit Python包进行APP的构建(2)
🗓️ 天 14 Streamlit 组件s Streamlit 组件s 是第三方的 Python 模块,对 Streamlit 进行拓展 [1]. 有哪些可用的 Streamlit 组件s? 好几十个精选 Streamlit 组件s 罗列在 Streamlit 的网站上 [2]. Fanilo(一位 Streamlit 创作者)在 wiki 帖子中组织了一个很棒的 St…...

Leecode热题100---46:全排列(递归)
题目: 给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。 思路: 元素交换函数递归: 通过交换元素来实现全排列。即对于[x, nums.size()]中的元素,for循环遍历每个元素分别成…...

Android 多语言
0. Locale方法 Locale locale Locale.forLanguageTag("zh-Hans-CN"); 执行如下方法返回字符串如下: 方法 英文下执行 中文下执行 备注 getLanguage()zhzhgetCountry()CNCNgetDisplayLanguage()zh中文getDisplayCountry()CN中国getDisplayName()zh (…...

Thingsboard规则链:Message Type Filter节点详解
一、Message Type Filter节点概述 二、具体作用 三、使用教程 四、源码浅析 五、应用场景与案例 智能家居自动化 工业设备监控 智慧城市基础设施管理 六、结语 在物联网(IoT)领域,数据处理与自动化流程的实现是构建智能系统的关键。作…...
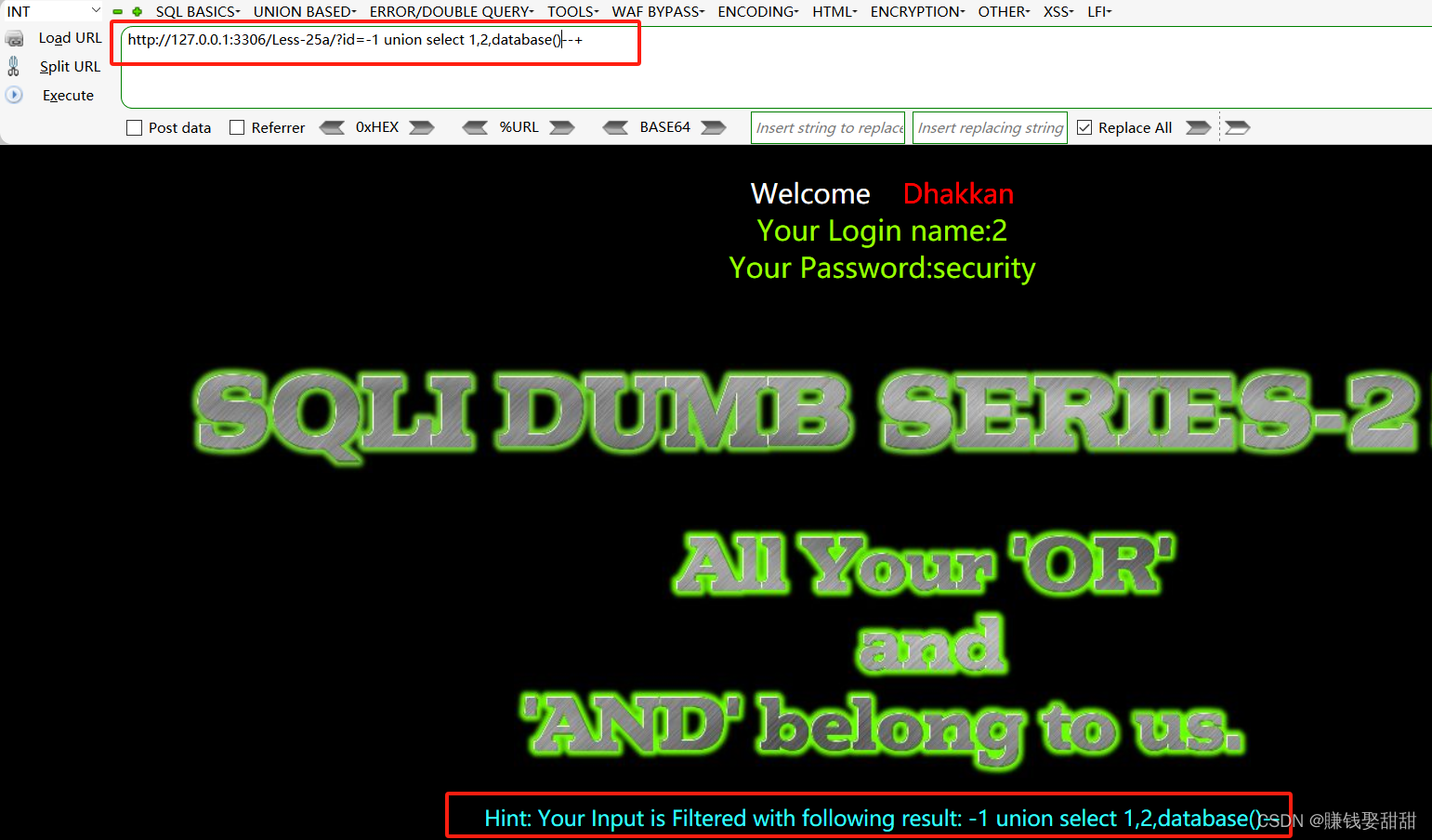
SQLI-labs-第二十五关和第二十五a关
目录 第二十五关 1、判断注入点 2、判断数据库 3、判断表名 4、判断字段名 5、获取数据库的数据 第二十五a关 1、判断注入点 2、判断数据库 第二十五关 知识点:绕过and、or过滤 思路: 通过分析源码和页面,我们可以知道对and和or 进…...

Windows、Linux添加路由
目录 一、Windows添加路由 1. 查看路由规则 2. 添加路由规则 3. 添加默认路由 4. 删除路由规则 二、Linux添加路由 1. 查看路由 2. 添加路由 3. 删除路由 4. 修改路由 5. 临时路由 6. 默认网关设置 一、Windows添加路由 1. 查看路由规则 route print 2. 添加…...

Swift 初学者交心:在 Array 和 Set 之间我们该如何抉择?
概述 初学 Swift 且头发茂密的小码农们在日常开发中必定会在数组(Array)和集合(Set)两种类型之间的选择中“摇摆不定”,这也是人之常情。 Array 和 Set 在某些方面“亲如兄弟”,但实际上它们之间却有着“云…...

C++ 类模板 函数模板
类模板 #include <bits/stdc.h> using namespace std; //多少变量就写多少个 template<typename T1, typename T2> class Cat { public:Cat(){}Cat(T1 name, T2 age){this->age age;this->name name;}void print(){cout << this->name << …...

OTP8脚-全自动擦鞋机WTN6020-低成本语音方案
一,产品开发背景 首先,随着人们生活质量的提升,对鞋子的保养需求也日益增加。鞋子作为人们日常穿着的重要组成部分,其清洁度和外观状态直接影响到个人形象和舒适度。因此,一种能够自动清洁和擦亮鞋子的设备应运而生&am…...
GpuMall智算云:meta-llama/llama3/Llama3-8B-Instruct-WebUI
LLaMA 模型的第三代,是 LLaMA 2 的一个更大和更强的版本。LLaMA 3 拥有 35 亿个参数,训练在更大的文本数据集上GpuMall智算云 | 省钱、好用、弹性。租GPU就上GpuMall,面向AI开发者的GPU云平台 Llama 3 的推出标志着 Meta 基于 Llama 2 架构推出了四个新…...
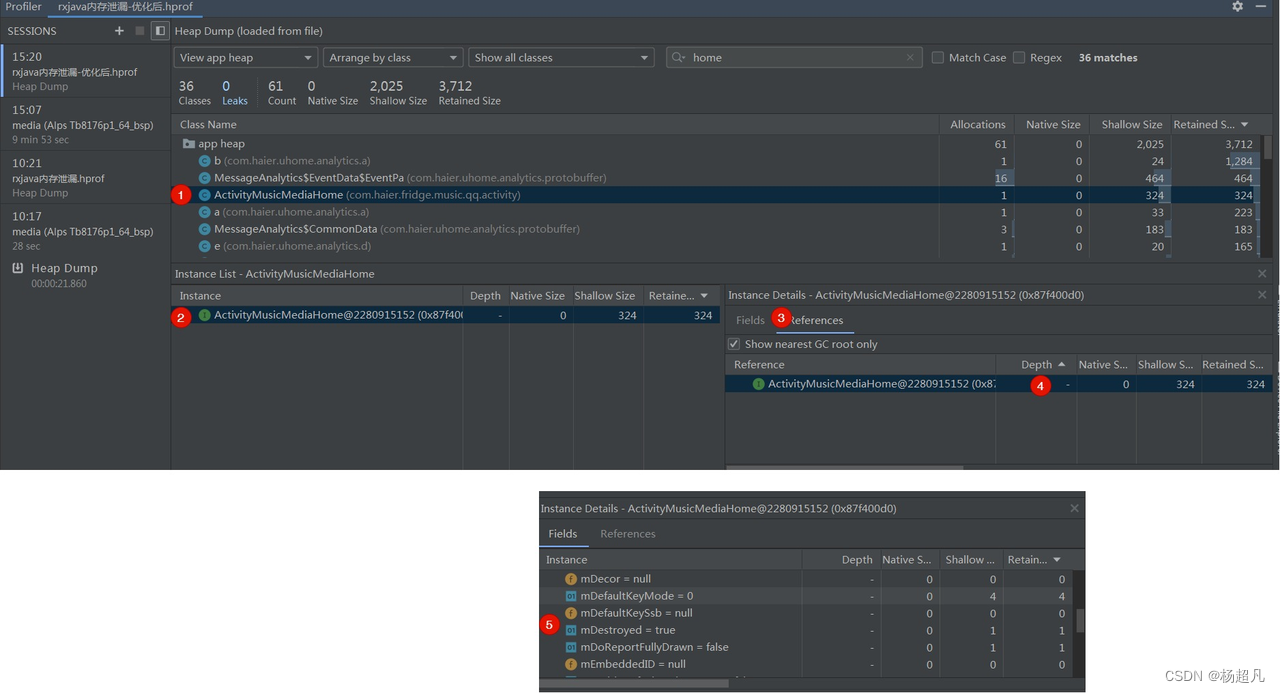
内存泄漏案例分享4-异步任务流内存泄漏
案例4——异步任务内存泄漏 异步任务,代指起子线程异步完成一些数据操作、网络接口请求等,通常会使用以下API: Runnbale,Thread,线程池RxJavaHandlerThread 而这些异步任务很有可能操作内存泄漏,下面我们以Rxjava为…...
【机器学习300问】100、怎么理解卷积神经网络CNN中的池化操作?
一、什么是池化? 卷积神经网络(CNN)中的池化(Pooling)操作是一种下采样技术,其目的是减少数据的空间维度(宽度和高度),同时保持最重要的特征并降低计算复杂度。池化操作不…...

RPA机器人流程自动化如何优化人力资源工作流程
人力资源部门在支持员工和改善整体工作环节方面扮演着至关重要的角色,但是在人资管理的日常工作中,充斥着大量基于规则的重复性任务,例如简历筛选、面试安排、员工数据管理、培训管理、绩效管理等,这些任务通常需要工作人员花费大…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...
