【鱼眼镜头11】Kannala-Brandt模型和Scaramuzza多项式模型区别,哪个更好?
Kannala-Brandt模型和Scaramuzza多项式模型在描述鱼眼相机畸变时都有其特定的数学表示和应用,但它们之间存在一些区别。以下是对两者区别的分点表示和归纳:
-
数学表示:
- Kannala-Brandt模型:它假设图像光心到投影点的距离和角度的多项式存在比例关系。具体地,它涉及到相机坐标系、图像坐标系、物点坐标、入射角、畸变像点和非畸变像点等参数,并通过这些参数之间的关系来描述径向畸变。
- Scaramuzza多项式模型:此模型通常采用多项式函数来描述相机镜头的畸变,特别适用于鱼眼相机。通过选择适当的多项式阶数,它可以模拟不同类型的鱼眼相机畸变。多项式中的系数通常需要通过相机标定来确定。
-
应用与特点:
- Kannala-Brandt模型:由于其特定的数学假设,它适用于描述鱼眼相机的径向畸变。该模型能够很好地处理鱼眼相机由于极端短焦和广角而产生的剧烈畸变。
- Scaramuzza多项式模型:由于其多项式形式的灵活性,它可以模拟包括鱼眼相机在内的多种类型相机的畸变。通过调整多项式的阶数和系数,它可以适应不同品牌和型号的鱼眼相机。
-
参数确定:
- 对于两种模型,其参数(如多项式系数)通常需要通过相机标定来确定。标定过程通常包括拍摄一组已知空间坐标的标定物图像,并通过最小化标定物上点的实际坐标与其在图像上的投影坐标之间的差异来求解模型参数。
-
适用范围:
- 两者都主要用于鱼眼相机的畸变建模,但Kannala-Brandt模型由于其特定的假设可能更适合于处理某些类型的鱼眼相机畸变,而Scaramuzza多项式模型则由于其灵活性而具有更广泛的应用范围。
总结来说,Kannala-Brandt模型和Scaramuzza多项式模型在描述鱼眼相机畸变时都有其独特的方法,但它们在数学表示、应用特点、参数确定和适用范围等方面存在差异。选择哪种模型取决于具体的应用场景和需求。
谁更好?
在比较Kannala-Brandt模型和Scaramuzza多项式模型哪个更好时,需要考虑多个因素,包括模型的适用性、灵活性、准确性以及是否支持自动标定等。以下是对这两个模型的比较和分析:
-
适用性:
- Kannala-Brandt模型:该模型能够很好地适用于普通、广角以及鱼眼镜头,特别是在处理鱼眼相机的径向畸变时表现出色。然而,它主要关注径向畸变的建模,对于其他类型的畸变可能不够准确。
- Scaramuzza多项式模型:此模型采用泰勒多项式来建模,可以同时适用于catadioptric(相机+镜子)和dioptric(鱼眼)两种全向相机。它不仅可以模拟径向畸变,还可以模拟其他类型的畸变,因此具有更广泛的适用性。
-
灵活性:
- Kannala-Brandt模型:由于其特定的数学假设和参数设置,可能对于某些特定类型的鱼眼相机具有较好的建模效果,但对于其他类型的相机可能需要调整或修改模型。
- Scaramuzza多项式模型:通过选择不同阶数的多项式,该模型可以灵活地适应不同类型的鱼眼相机和折反射相机。此外,它还可以适应市场上各种鱼眼镜头,其视野可达195度。
-
准确性:
- 准确性在很大程度上取决于模型参数的标定和图像数据的质量。由于两个模型都经过了广泛的实验验证和应用,因此在适当的应用场景下都可以获得相对准确的标定结果。然而,对于特定的相机和镜头,可能需要根据实际情况选择更适合的模型。
-
自动标定:
- Kannala-Brandt模型:文章中没有明确提到该模型是否支持自动标定。通常情况下,模型参数的标定需要手动进行或依赖于特定的标定软件。
- Scaramuzza多项式模型:该模型所在的工具箱提供了自动标定功能,即畸变中心和标定点都是自动检测的,无需用户干预。这使得标定过程更加简便和高效。
综上所述,Scaramuzza多项式模型在适用性、灵活性和自动标定方面具有优势。然而,在实际应用中,还需要根据具体的相机类型、镜头参数和应用场景来选择最适合的模型。此外,还需要注意标定数据的准确性和可靠性对于模型性能的影响。
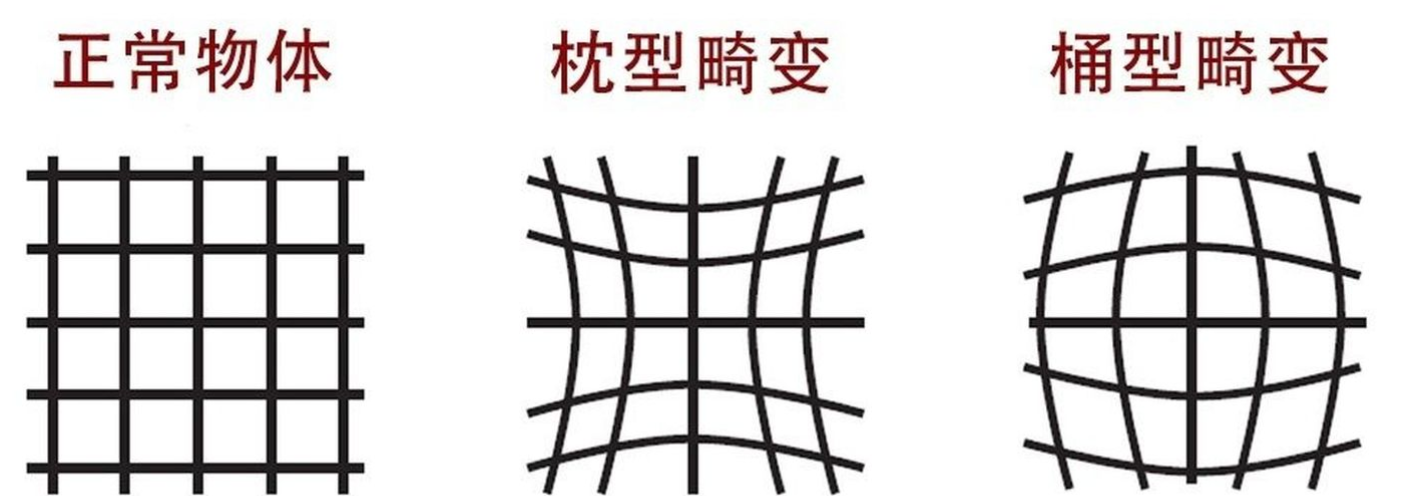
径向畸变表式沿半径方向的偏移量, 径向畸变的形成原因是镜头制造工艺不完美,使得镜头形状存在缺陷, 通常又分为桶性畸变和枕形畸变,dr 分别代表 往外偏和往里偏.
上述内容的理解你需要阅读博客
【鱼眼镜头9】论文Omnidirectional Camera,鱼眼是全向相机的折射相机的一种重要类型,满足单一有效视点的特性, Taylor模型(适用于鱼眼相机),统一投影模型(在鱼眼应用受限)
相关文章:
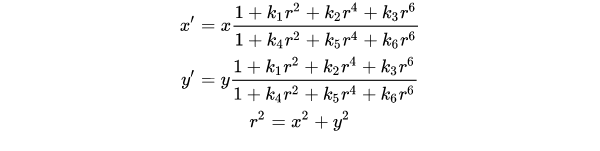
【鱼眼镜头11】Kannala-Brandt模型和Scaramuzza多项式模型区别,哪个更好?
Kannala-Brandt模型和Scaramuzza多项式模型在描述鱼眼相机畸变时都有其特定的数学表示和应用,但它们之间存在一些区别。以下是对两者区别的分点表示和归纳: 数学表示: Kannala-Brandt模型:它假设图像光心到投影点的距离和角度的多…...
微信小程序仿胖东来轮播和背景效果(有效果图)
效果图 .wxml <view class"swiper-index" style"--width--:{{windowWidth}}px;"><image src"{{swiperList[(cardCur bgIndex -1?swiperList.length - 1:cardCur bgIndex > swiperList.length -1?0:cardCur bgIndex)]}}" clas…...

10.SpringBoot 统一处理功能
文章目录 1.拦截器1.1在代码中的应用1.1.1定义拦截器1.1.2注册配置拦截器 1.2拦截器的作用1.3拦截器的实现 2.统一数据返回格式2.1 为什么需要统⼀数据返回格式?2.2 统⼀数据返回格式的实现 3.统一异常处理4.SpringBoot专业版创建项目无Java8版本怎么办?…...

【八股系列】为什么会有webpack配置?webpack的构建流程是什么?
文章目录 1. webpack是什么?2. 为什么需要webpack?3. webpack构建原理4. 构建流程通常包括以下步骤5. Webpack构建流程图 1. webpack是什么? Webpack是一个模块打包工具,它可以将项目中的各种静态资源,如JavaScript、…...

sdf 测试-2-openssl
任务详情 在openEuler(推荐)或Ubuntu或Windows(不推荐)中完成下面任务,参考网内容 和AI要给出详细过程,否则不得分。 0. 根据gmt0018标准,如何调用接口实现基于SM3求你的学号姓名的SM3值?(5‘) 使用OpenSSL实现SDF接…...

头歌springboot初体验
您好!看起来您可能在询问关于Spring Boot的入门体验。Spring Boot是一个开源的Java框架,它设计用来简化Spring应用程序的初始搭建和开发过程。以下是一些Spring Boot的基本概念和入门步骤: Spring Boot简介: Spring Boot是Spring框…...
矩阵对角化在机器学习中的奥秘与应用
在机器学习的广阔领域中,矩阵对角化作为一种重要的数学工具,扮演着不可或缺的角色。从基础的线性代数理论到复杂的机器学习算法,矩阵对角化都在其中发挥着重要的作用。 矩阵对角化的概念与原理 矩阵对角化是矩阵理论中的一个基本概念&#x…...

操作MySQL数据库
【一】针对库的增删查改(文件夹) 【1】创建数据库 (1)语法 创建一个存储数据表的文件夹。 注意:mysql中的编码字符集中utf-8,要换成utf8mb4。SQL语句中的中括号部分表示可选。 create database [if no…...
)
Linux shell 文件生成文件脚本(模拟生成文件、生成大量文件)
文章目录 Linux shell 文件生成文件脚本 Linux shell 文件生成文件脚本 TARGET_DIR:生成文件路径 NUM_FILES:生成文件数量 FILE_SIZE:生成文件大小(KB) #!/bin/bashset -e set -u# Directory where files will be cr…...

theharvester一键收集域名信息(KALI工具系列十)
目录 1、KALI LINUX简介 2、theharvester工具简介 3、在KALI中使用theharvester 3.1 用搜索引擎扫描 3.2 扫描并输出结果 3.3 扫描某域名下的所有账号 3.4 使用所有的搜索引擎扫描 4、总结 1、KALI LINUX简介 Kali Linux 是一个功能强大、多才多艺的 Linux 发行版&…...

「动态规划」删除并获得点数
力扣原题链接,点击跳转。 给你一个整数数组nums。每次操作,可以删除任意一个值n,接着获得点数n,并同时删除所有的n-1和n1。你最多能获取多少点数? 这个问题的解法相当巧妙。我们可以把问题先转化一下。用类似计数排序…...

MongoDB CRUD操作:内嵌文档数组查询
MongoDB 内嵌文档数组查询 文章目录 MongoDB 内嵌文档数组查询查询数组内嵌文档为文档数组中的字段指定查询条件指定文档数组内嵌文档字段的查询条件使用数组索引查询内嵌文档的字段 为文档数组指定多个条件单个内嵌文档满足内嵌字段的多个查询条件符合标准的元素组合 使用 Mon…...
)
【C++】每日一题 50 Pow(x,n)
实现 pow(x, n) ,即计算 x 的整数 n 次幂函数(即,x^n )。 当需要计算x的n次幂时,可以使用递归或者迭代的方式来实现。 #include <iostream>double myPow(double x, int n) {if (n 0) {return 1.0;} else if (…...

HG/T 6088-2022 透水道路用涂料检测
透水混凝土是指由水泥、矿物掺合料、骨料、外加剂及水等主要材料经拌合形成的,具有透水功能的混凝土材料,用于其表面的涂料称为透水道路用涂料。 HG/T 6088-2022透水道路用涂料检测项目: 测试指标 测试方法 有害物质限量 GB 38468 在容器…...

linux定时清理docker日志脚本
Linux 定时清理 Docker 日志的脚本与配置指南 在使用 Docker 容器化应用程序时,日志文件可能会迅速增长,占用大量磁盘空间。为了保持系统的稳定性和高效运行,定期清理 Docker 日志文件是必要的。本文将介绍如何编写一个 Linux 脚本来清理 Docker 日志文件,并通过 cron 定时…...
ROS学习笔记(16):夹缝循迹
0.前言 在笔记的第15期对巡墙驾驶的原理进行了简单讲解,而这期我们来讲一下夹缝循迹,也常被叫follow the gap,也更新一些概念。 1.探索式路径规划与避障 1.概念 无预先建图的路径规划叫探索式路径规划,例如巡墙循迹和夹缝循迹&…...
-锁和事务语句)
【MySQL精通之路】SQL语句(3)-锁和事务语句
目录 1.START TRANSACTION、COMMIT和ROLLBACK语句 2.无法回滚的语句 3.导致隐含COMMIT的语句 4.SAVEPOINT、ROLLBACK TO SAVEPOINT和RELEASE SAVEPOINT语句 5.LOCK INSTANCE FOR BACKUP和UNLOCK INSTANCE语句 6.LOCK TABLE和UNLOCK TABLES语句 6.1 表锁获取 6.2 表锁释放…...
211大学计算机专业不考408,新增的交叉专业却考408!南京农业大学计算机考研考情分析!
南京农业大学信息科技学院可追溯至1981年成立的计算中心和1985年筹建的农业图书情报专业。1987年设立了农业图书情报系,1993 年农业图书情报系更名为信息管理系,本科专业名称也于1999年更名为信息管理与信息系统专业。1994年计算中心开始招收计算机应用专…...

利用java8 的 CompletableFuture 优化 Flink 程序,性能提升 50%
你好,我是 shengjk1,多年大厂经验,努力构建 通俗易懂的、好玩的编程语言教程。 欢迎关注!你会有如下收益: 了解大厂经验拥有和大厂相匹配的技术等 希望看什么,评论或者私信告诉我! 文章目录 一…...

香橙派 AIpro综合体验及AI样例运行
香橙派 AIpro综合体验及AI样例运行 环境: 香橙派版本: AIpro(8TOPSINT8) OS : Ubuntu 22.04.3 LTS(GNU/Linux 5.10.0 aarch64) (2024-03-18) 远程服务端1:OpenSSH 8.9p1 远程服务端2:TightVNC Server 1.3.10 远程客户端…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...