【动态规划】背包问题(01背包,完全背包)
Halo,这里是Ppeua。平时主要更新C语言,C++,数据结构算法......感兴趣就关注我吧!你定不会失望。
🌈个人主页:主页链接
🌈算法专栏:专栏链接
我会一直往里填充内容哒!
🌈LeetCode专栏:专栏链接
目前在刷初级算法的LeetBook 。若每日一题当中有力所能及的题目,也会当天做完发出
🌈代码仓库:Gitee链接
🌈点击关注=收获更多优质内容🌈
目录
DP:
题目:01背包问题
题解:
代码实现:
优化:
代码实现:
题目:完全背包
题解:
代码实现:
优化:
代码实现:
优化
代码实现:
完结撒花:
好**难啊,整抑郁了
DP:
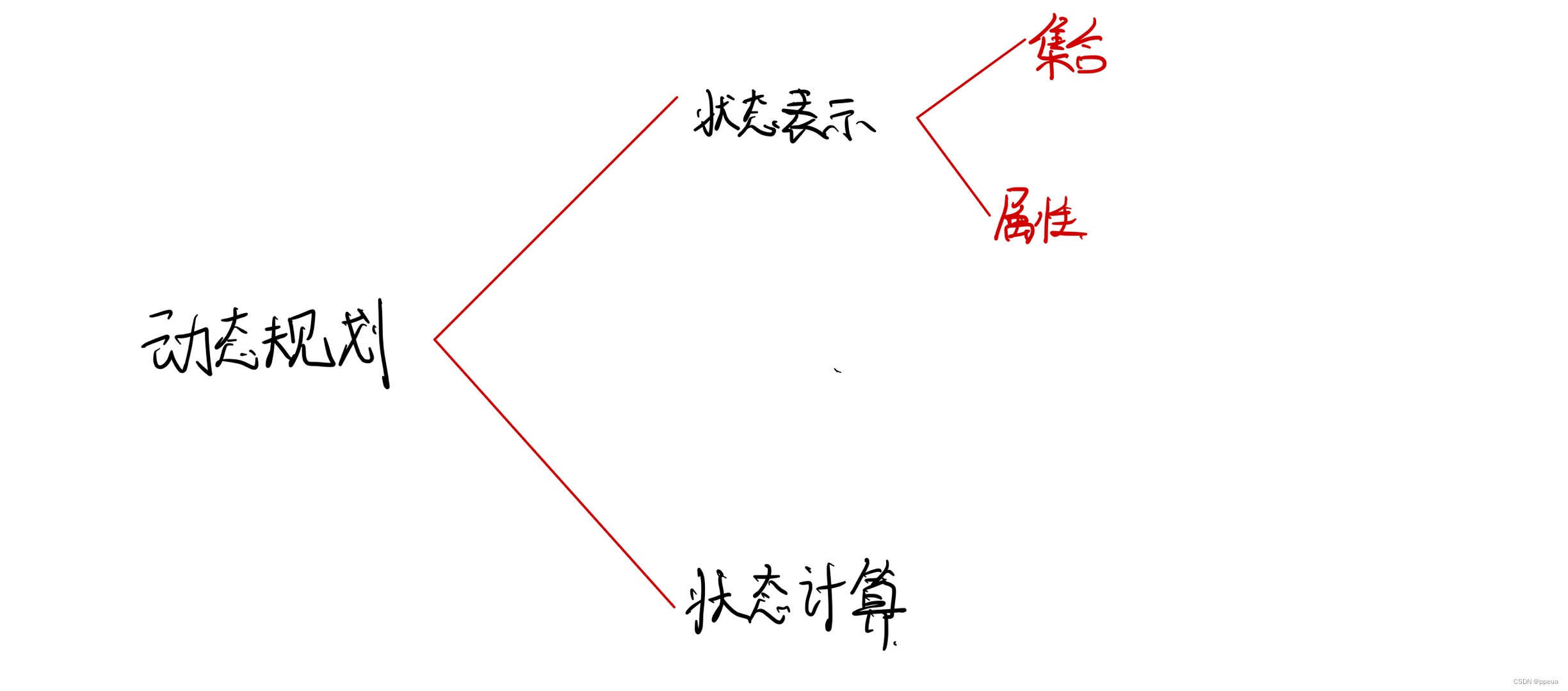
DP有这样的一个分析方法
题目:01背包问题
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i件物品的体积是 vi,价值是 wi
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。输入格式
第一行两个整数,N,V用空格隔开,分别表示物品数量和背包容积。
接下来有 N行,每行两个整数 vi,wi,用空格隔开,分别表示第 i件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000
0<vi,wi≤1000输入样例
4 5 1 2 2 4 3 4 4 5输出样例:
8
题解:
分析01背包问题的特点:有N件物品,背包容积是V,每件物品只能拿(0)或不拿(1),所以称为01背包问题.
将问题分析,当决定第i件拿与不拿的时候,表达式为:此时背包价值=max(背包没拿第i件物品的价值,拿了第i件物品的价值)
所以这里的状态表示的集合为:从前i件物品拿,且总体积不超过j
状态表示的属性为:最大值
状态计算为f[i][j],其中i为第几件物品,j为此时背包的容量
其中不选第i件物品总价值,就为前一个相同容量的背包中的价值
因为直接计算选第i件物品比较难计算,所以我们将选第i件物品的价值转换为,不选第i件物品的价值,并令其背包容积减去第i件物品的v再加上其价值w

所以我们的状态方程就为:f[i][j]=max(f[i-1],f[i-1][j-v]+w)
代码实现:
#include<iostream>
using namespace std;
int n, m;
const int N = 1010;
int v[N], w[N];
int f[N][N];
int solution1()
{cin >> n >> m;for (int i = 1; i <= n; i++)cin >> v[i] >> w[i];for (int i = 0; i <= m; i++)f[0][i] = 0;//一件物品都没选 0-m的容积下价值都为0for (int i = 1; i <= n; i++){for (int j = 0; j <= m; j++){f[i][j] = f[i - 1][j];if (j >= v[i])f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);//在拿i-1件物品,其容量为j-vi时放入物品的最大值 }}cout << f[n][m];
}
优化:
观察.f[i][j]的变换形式,每次计算只用到了上一层i,j,所以我们可以将i这一维给删了,变成这种形式
直接将[i]删了
int n, m;
const int N = 1010;
int v[N], w[N];
int f[N];
int main()
{cin >> n >> m;for (int i = 1; i <= n; i++)cin >> v[i] >> w[i];for (int i = 0; i <= m; i++)f[i] = 0;//一件物品都没选 0-m的容积下价值都为0for (int i = 1; i <= n; i++){for (int j = v[i]; j<=m; j++){f[j] = max(f[j], f[j - v[i]] + w[i]);//滚动数组优化,从后向前遍历,这样第一个的结果用到的是上一层的数据}}cout << f[m];
}
但观察此时的状态方程.
f[j-v[i]]+w[i],用到的是这一层已经计算的数据(因为j是从小开始算的,也就是说从小的j开始就会把上一次计算的j给覆盖了,而后面要用到的是上面一层i-1的数据,而不是i)
所以我们为了避免这种情况,使用i-1的数据,我们从后往前遍历,这样每一次计算j时,用的就是i-1层的数据,与上文所述一致
代码实现:
int n, m;
const int N = 1010;
int v[N], w[N];
int f[N];
int main()
{cin >> n >> m;for (int i = 1; i <= n; i++)cin >> v[i] >> w[i];for (int i = 0; i <= m; i++)f[i] = 0;//一件物品都没选 0-m的容积下价值都为0for (int i = 1; i <= n; i++){for (int j = m; j >= v[i]; j--){f[j] = max(f[j], f[j - v[i]] + w[i]);//滚动数组优化,从后向前遍历,这样第一个的结果用到的是上一层的数据}}cout << f[m];
}题目:完全背包
有 N种物品和一个容量是 V 的背包,每种物品都有无限件可用。
第 i种物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。输入格式
第一行两个整数N,V,用空格隔开,分别表示物品种数和背包容积。
接下来有 N行,每行两个整数 vi,wi,用空格隔开,分别表示第 i 种物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000
0<vi,wi≤1000输入样例
4 5 1 2 2 4 3 4 4 5输出样例:
10
题解:
完全背包问题是01背包问题的升级版.每件物品不再只能拿一件,而可以无限拿(在容量允许的情况下)
将问题分析,当决定第i件拿K件,表达式为:此时背包价值=max(背包没拿第i件物品的价值,拿了K*第i件物品的价值)
所以这里的状态表示的集合为:从前i件物品拿K件,且总体积不超过j
状态表示的属性为:最大值
状态计算为f[i][j],其中i为第几件物品,j为此时背包的容量
其中不选第i件物品总价值,就为前一个相同容量的背包中的价值
因为直接计算拿第i件k个比较难计算,所以我们将选第i件物品的价值转换为,不选第i件物品的价值,并令其背包容积减去第i件物品的K*v再加上其价值K*w

代码实现:
#include <algorithm>
#include<iostream>
using namespace std;
int n, m;
const int N = 1010;
int v[N], w[N];
int f[N][N];
int main()
{for (int i = 1; i <= n; i++)cin >> v[i] >> w[i];for (int i = 0; i <= m; i++)f[0][i] = 0;//一件物品都没选 0-m的容积下价值都为0for(int i=1;i<=n;i++){for(int j=0;j<=m;j++){for(int k=0;k*v[i]<=j;k++){f[i][j]=f[i-1][j];if(j>=k*v[i])f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);}}}cout<<f[n][m];
}这和01背包问题的朴素做法几乎一模一样,但这里的时间复杂度为n^3,所以我们得优化一下,不然就TLE了
优化:
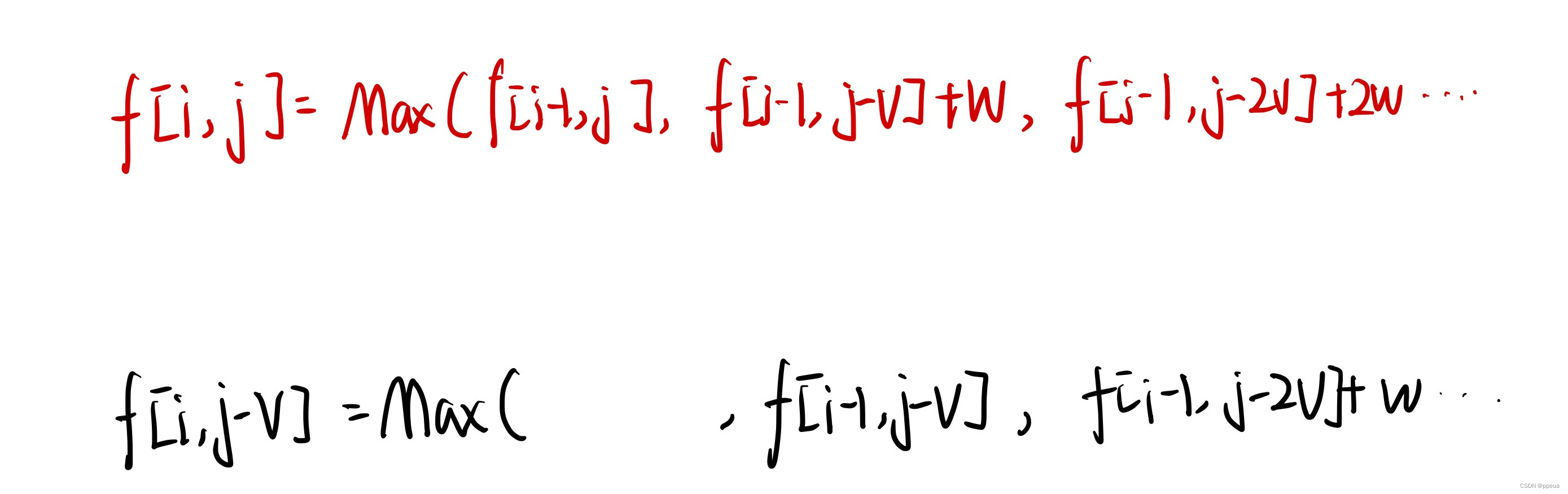
对于f[i,j-v]的含义是:将J>=K*V时,我们先将第i个物品放入背包,之后再去找当前容量下能放入的最大价值的东西,之后再加上w,这时候就可以不用考虑具体放几件了,
最后也就变成了f[i][j]=Max(f[i-1][j],f[i][j-v]+w)
代码实现:
#include <algorithm>
#include<iostream>
using namespace std;
int n, m;
const int N = 1010;
int v[N], w[N];
int f[N][N];
int main()
{cin>>n>>m;for (int i = 1; i <= n; i++)cin >> v[i] >> w[i];for (int i = 0; i <= m; i++)f[0][i] = 0;//一件物品都没选 0-m的容积下价值都为0for(int i=1;i<=n;i++){for(int j=0;j<=m;j++){f[i][j]=f[i-1][j];if(j>=v[i])f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);//表示已经选入第i层 }}cout<<f[n][m];
}优化
因为还是N^2,观察这个表达式,和01背包问题很想,且也只用到了i-1层 所以可以用滚动数组优化,删掉一维即可,因为这里计算max的时候用的式i 所以不用进行从大到小的处理
代码实现:
#include <algorithm>
#include<iostream>
using namespace std;
int n, m;
const int N = 1010;
int v[N], w[N];
int f[N];
int main()
{cin>>n>>m;for (int i = 1; i <= n; i++)cin >> v[i] >> w[i];for (int i = 0; i <= m; i++)f[i] = 0;//一件物品都没选 0-m的容积下价值都为0for(int i=1;i<=n;i++){for(int j=v[i];j<=m;j++){f[j]=max(f[j],f[j-v[i]]+w[i]);//表示已经选入第i层 }}cout<<f[m];
}完结撒花:
🌈本篇博客的内容【动态规划 :背包问题(01背包,完全背包)】已经结束。
🌈若对你有些许帮助,可以点赞、关注、评论支持下博主,你的支持将是我前进路上最大的动力。
🌈若以上内容有任何问题,欢迎在评论区指出。若对以上内容有任何不解,都可私信评论询问。
🌈诸君,山顶见!
相关文章:
【动态规划】背包问题(01背包,完全背包)
Halo,这里是Ppeua。平时主要更新C语言,C,数据结构算法......感兴趣就关注我吧!你定不会失望。 🌈个人主页:主页链接 🌈算法专栏:专栏链接 我会一直往里填充内容哒! &…...
记录 UE5 完全重新构建 UE C++项目
不知道搞了什么,C项目的实时代码编译罢工了,搞了半天都修不好,只能又重建了 UE5 版本为 v5.1.1 删除以下文件夹 /Binaries /Intermediate /SavedBinaries 文件夹是编译后的模块 Intermediate 文件夹里是中间层的C代码,完全由ue…...
java版云HIS系统源码 微服务架构支持VUE
云his系统源码 一个好的HIS系统,要具有开放性,便于扩展升级,增加新的功能模块,支撑好医院的业务的拓展,而且可以反过来给医院赋能,最终向更多的患者提供更好地服务。 私信了解更多! 本套基于…...

苹果内购支付检验错误码
21000 The request to the App Store didn’t use the HTTP POST request method. 对App Store的请求没有使用HTTP POST请求方法。 21001 The App Store no longer sends this status code. App Store不再发送此状态代码。 21002 The data in the receipt-data property…...

day27_css
今日内容 上课同步视频:CuteN饕餮的个人空间_哔哩哔哩_bilibili 同步笔记沐沐霸的博客_CSDN博客-Java2301 零、 复习昨日 一、CSS 零、 复习昨日 见代码 一 、引言 1.1CSS概念 层叠样式表(英文全称:Cascading Style Sheets)是一种用来表现HTML(标准通…...

智慧赋能,聚力开源——第四届OpenI/O 启智开发者大会开源治理专场顺利举办!
为汇聚国内外知名开源组织共同探讨中国开源生态建设及开源治理相关议题,推进产学研用开源合作,2月24日下午,第四届OpenI/O启智开发者大会在深圳人才研修院智汇中心举办以“构建开源联合体,共建开源生态”为主题的开源治理专场分论…...

Java工程师应该如何成长?
近几年,不少开发者会抱怨“面试造火箭,天天拧螺丝”,每天进行重复业务开发,似乎能力被日常工作限制,无法突破提高。 极客时间《Java 核心技术 36 讲》专栏作者杨晓峰认为,如果处于新手阶段,全面…...

【数据分析师求职面试指南】必备编程技能整理之Hive SQL必备用法
文章目录熟悉Python懂R语言掌握SQL大数据基础数据库常用类型多表查询更多聚合函数distinctcase when窗口函数动态更新一行变多行调优内容整理自《拿下offer 数据分析师求职面试指南》—徐粼著 第四章编程技能考查其他内容:【数据分析师求职面试指南】必备基础知识整…...

Maven - Linux 服务器 Maven 环境安装与测试
目录 一.引言 二.安装流程 1.获取安装包 2.解压并安装 3.配置环境 4.mvn 验证 三.测试踩坑 1.Permission denied 2.Plugin or dependencies Error 一.引言 通道机上的 java 项目需要 mvn package 提示没有 mvn 命令,下面记录下安装 maven 的全过程。 二.安…...

5G模块可以注册到4G,不能注册到5G;SIM卡接到5G手机是可以注册到5G网络的?
5G网络覆盖范围较小或者信号质量不佳。在这种情况下,您可以尝试移动到不同的位置,以获得更好的信号质量和覆盖范围。 目前,5G网络已经在全球多个国家和地区推出,并且在不断扩大覆盖范围。以下是一些已经拥有5G覆盖的主要地区&…...

宝塔webhook自动化打包vue项目时,npm不生效问题
文章目录📋前言🎯查看webhook配置的代码🎯测试代码,检查输出内容🎯解决方法📋前言 这篇文章主要是记录和解决在宝塔面板中,webhook自动化打包vue项目时,npm不生效问题。说来奇怪&am…...

嵌入式 Linux进程间通信之信号量
目录 一、信号量 1、信号量概述 2、什么是信号量 3、信号量的分类 4、进程获取共享资源要执行的操作 5、System V IPC 机制:信号量 5.1 semget函数 5.2 semop函数 5.3 semctl函数 一、信号量 1、信号量概述 信号量集:由若干个信号组成的集合&a…...
谷粒学院开发(一):基础准备
商业模式 常见商业模式 B2C模式: 两个角色: 管理员:增加,修改,删除普通用户:查询 商家到用户,自己制作大量自有版权的视频,放在自有平台上,让用户付费。 这是这个项目使…...
Photoshop如何安装ZXP扩展插件?
Photoshop如何安装ZXP扩展插件呢?有一些小伙伴不会安装,今天介绍两种安装ZXP扩展的方法,希望对能帮助到大家。方法一:手动安装方式1)把下载好的.zxp扩展名改为.zip,然后解压。Windows系统:C:\Us…...

c++面试技巧-基础篇4
1.面试官:在使用继承时需要注意哪些问题? 应聘者:在使用继承时需要注意以下内容。 (1)父类的构造函数和析构函数是不会被继承的,需要重写派生类的构造函数和析构函数。 (2)派生类…...
openEuler用户软件仓(EUR)介绍
什么是 EUR EUR(openEuler User Repo)是openEuler社区针对开发者推出的个人软件包托管平台,目的在于为开发者提供一个易用的软件包分发平台。 链接:https://eur.openeuler.openatom.cn/ 为什么我们需要 EUR 在操作系统的世界,软件包是一等…...
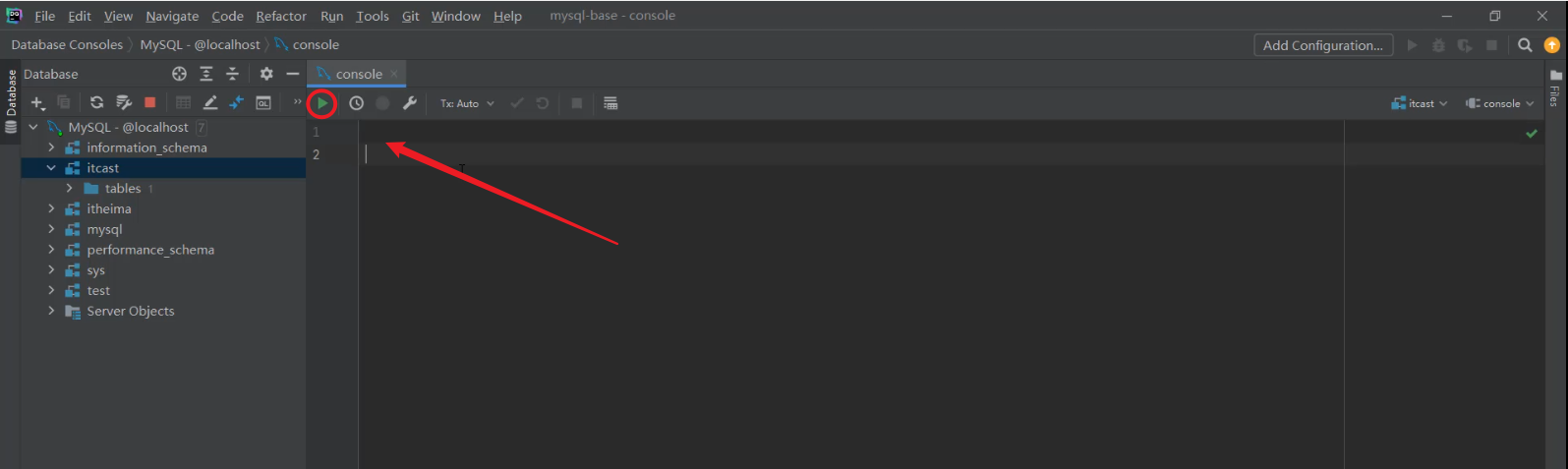
MySQL的图形化界面开发工具DataGrip的下载安装
在日常的开发中,会借助于MySQL的图形化界面,来简化开发,提高开发效率。目前mysql主流的图形化界面工具,有Navicat、SQLyog、DataGrip等,最后一种DataGrip,这种图形化界面工具,功能更加强大&…...

Azure Portal 访问安全性增强
Azure Portal 访问安全性增强客户需求如何设置账号(包括Admin)定期修改密码,例如强制每90天必须修改密码如何设定账号密码的复杂性要求如何设定限制访问Azure Portal的源IP Address客户需求 为了增强访问Azure Portal的安全性,希…...

mysql安全值守数据库常用语句
目录1.用户权限设置mysql中用户如何定义2.元数据查询3.union查询详解4.分组查询展示5.字符串函数6.mysql数据库导入导出1.用户权限设置 mysql中用户如何定义 用户名主机域有以下几种表示方式: 1. 10.0.0.51 2. 10.0.0.% 3. % 4. 10.0.0.0/255.255.255.0 5. Db01 6…...
CSS快速入门
文章目录一、CSS是什么?语法规范引入方式二、CSS选择器标签选择器类选择器ID选择器通配符选择器后代选择器子选择器并集选择器伪类选择器三、常见元素属性字体属性文本属性背景属性圆角矩形元素的显示默认块级与行级元素盒子模式去除浏览器默认样式弹性布局一、CSS是…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...
