C-数据结构-树状存储的基本实现
/*
理解和记忆递归的关键在于把握递归的本质和函数调用的过程。递归函数在每次调用时会把当前状态压入调用栈,直到满足终止条件后开始回溯。理解基准条件和递归步骤:每个递归函数都需要有基准条件(如节点为空时返回),并在每一步中递归调用自身处理子问题。
*/
main.c
#include<stdio.h>
#include<stdlib.h>#define NAMESIZE 32struct score_st
{int id;char name[NAMESIZE];int math;int chinese;
};struct node_st
{struct score_st data;struct node_st *l,*r;
};print_s(struct score_st *d)
{printf("%d %s %d %d\n",d->id,d->d.name,d->math,d->chinese);
}int insert(struct node_st **root,struct score_st *data)
{struct node_st *node;if(*root == NULL){node = malloc(sizeof(*node));if(node == NULL)return -1;node->data = *data;node->l = NULL;node->r = NULL;*root = node;return 0;}if(data->id <= (*root)->data.id)return insert(&(*root)->l,data);elsereturn insert(&(*root)->r,data);
}
struct score_st *find(struct node_st *root,int id)
{if(root == NULL)return NULL;if(id == root->data.id)return &root->data;if(id < root->data.id)return find(root->l,id);elsereturn find(root->r,id);
}
void draw_(struct node_st *root,in level)
{int i;if(root == NULL)return ;draw_(root->t,level+1);for(i = 0;i<level;i++)printf(" ");print_s(&root->data);draw_(root->l,level+1);
}
void draw(struct node_st *root)
{draw_(root,0);
}int main()
{int arr[] = {1,2,3,7,6,5,9,8,4};int i;struct score_st tmp,*datap;struct node_st *tree = NULL;for(i = 0;i<sizeof(arr)/sizeof(*arr);i++){tmp.id = arr[i];snprintf(tmp.name,NAMESIZE,"stu%d",arr[i]);tmp.math = rand()%100;tmp.chinese = rand()%100;insert(&tree,&tmp);}draw(tree);#if 0int tmpid = 2;datap = find(tree,tmpid);if(datap == NULL)printf("can not find the id %d\n",tmpid);elseprint_s(datap);
#endifexit(0);
}补充说明1
为了理解二级指针的一级目标,我们需要明确指针和二级指针的概念。
指针和二级指针
- 指针:一个指针变量保存了另一个变量的地址。通过指针,我们可以访问或修改这个变量的值。例如,
int *p是一个指向整数的指针变量。 - 二级指针:一个二级指针变量保存了另一个指针变量的地址。通过二级指针,我们可以访问或修改这个指针变量的值。例如,
int **pp是一个指向指针变量的指针。
二级指针的一级目标
一级目标是指二级指针所指向的那个指针变量。
举个具体的例子,假设我们有以下定义:
int a = 10; // 普通变量
int *p = &a; // 指向变量 a 的指针
int **pp = &p; // 指向指针 p 的指针
在这个例子中:
p是一个指向a的指针。pp是一个指向p的指针。
我们可以这样理解:
pp保存了p的地址。*pp解析出pp所指向的内容,即p。**pp解析出*pp所指向的内容,即a的值。
当然可以!以下是一个图形示例来说明*aa = b的含义:
假设:
aa是一个指向指针的指针。a是一个指针,它最初指向一个地址。b是另一个指针,指向另一个地址。
初始状态:
+------+ +------+ +------+
| aa | -> | a | -> | x | (假设 x 是 a 所指向的值)
+------+ +------+ +------++------+ +------+
| b | -> | y | (假设 y 是 b 所指向的值)
+------+ +------+
执行 *aa = b 后的状态:
+------+ +------+
| aa | -> | b | -> | y | (aa 现在指向 b,而 b 仍然指向 y)
+------+ +------+
这样做后,aa 所指向的指针 a 不再指向原来的地址,而是指向了 b 所指向的地址。
以下是更详细的图示:
- 初始状态:
aa -> a -> [地址1: x]
b -> [地址2: y]
- 执行
*aa = b后:
aa -> b -> [地址2: y]
这意味着,aa 原本指向的指针 a,现在指向了 b,即 a 的地址已经被 b 的地址覆盖。
希望这个图形示例能帮助你更好地理解 *aa = b 的含义。如果还有其他问题,请随时告诉我!
补充说明2
你提到的情况是正确的。A 不出栈的原因是递归调用还没有完成。为了更清楚地解释递归调用的过程,让我们重新逐步分析每一个递归调用和返回的过程,并使用栈来跟踪函数调用。
示例二叉树
假设有如下二叉树:
A/ \B C/ \D E
使用栈模拟执行过程
我们以栈的方式逐步模拟 draw 函数调用 draw_ 的过程。
-
初始状态:
- 栈为空。
- 调用
draw(root),进入draw_(root, 0)。
-
处理根节点
A:- 调用
draw_(A, 0)。 - 栈:[
draw_(A, 0)]
- 调用
-
递归处理右子树
C:- 调用
draw_(C, 1)。 - 栈:[
draw_(A, 0),draw_(C, 1)]
- 调用
-
处理
C节点:- 右子树为空,返回。
- 打印
C(缩进 4 空格)。 - 左子树为空,返回。
- 返回
draw_(A, 0)。 - 栈:[
draw_(A, 0)]
输出:
C -
打印根节点
A:- 打印
A(无缩进)。 - 栈:[
draw_(A, 0)]
输出:
C A - 打印
-
递归处理左子树
B:- 调用
draw_(B, 1)。 - 栈:[
draw_(A, 0),draw_(B, 1)]
- 调用
-
处理
B节点:- 调用
draw_(E, 2)(递归处理右子树)。 - 栈:[
draw_(A, 0),draw_(B, 1),draw_(E, 2)]
- 调用
-
处理
E节点:- 右子树为空,返回。
- 打印
E(缩进 8 空格)。 - 左子树为空,返回。
- 返回
draw_(B, 1)。 - 栈:[
draw_(A, 0),draw_(B, 1)]
输出:
C AE -
打印
B节点:- 打印
B(缩进 4 空格)。 - 栈:[
draw_(A, 0),draw_(B, 1)]
输出:
C AEB - 打印
-
递归处理左子树
D:- 调用
draw_(D, 2)。 - 栈:[
draw_(A, 0),draw_(B, 1),draw_(D, 2)]
- 调用
-
处理
D节点:- 右子树为空,返回。
- 打印
D(缩进 8 空格)。 - 左子树为空,返回。
- 返回
draw_(B, 1)。 - 栈:[
draw_(A, 0),draw_(B, 1)]
输出:
C
AEBD
-
完成
B节点的处理:- 返回
draw_(A, 0)。 - 栈:[
draw_(A, 0)]
- 返回
-
完成
A节点的处理:- 返回
draw(root)。 - 栈为空。
- 返回
最终输出
C
AEBD
在这个过程中,A 不出栈的原因是因为它的递归调用还没有完成。只有当左子树 B 的所有处理完成后,A 才会出栈,回到 draw(root),表示递归完全结束。这样我们可以准确地跟踪每一步的递归调用和返回,理解栈的作用。
希望这个解释能帮助你更好地理解代码的递归逻辑!如果还有其他问题,请随时告诉我。
相关文章:

C-数据结构-树状存储的基本实现
/* 理解和记忆递归的关键在于把握递归的本质和函数调用的过程。递归函数在每次调用时会把当前状态压入调用栈,直到满足终止条件后开始回溯。理解基准条件和递归步骤:每个递归函数都需要有基准条件(如节点为空时返回),并…...

指纹识别经典图书、开源算法库、开源数据库
目录 1. 指纹识别书籍 1.1《精通Visual C指纹模式识别系统算法及实现》 1.2《Handbook of Fingerprint Recognition》 2. 指纹识别开源算法库 2.1 Hands on Fingerprint Recognition with OpenCV and Python 2.2 NIST Biometric Image Software (NBIS) 3. 指纹识别开源数…...

嵌入式之译码器
系列文章目录 译码器嵌入式之译码器 嵌入式之译码器 系列文章目录一、译码器定义二、常见类型的译码器三、工作原理 一、译码器定义 译码器(Decoder)是一种数字电路,其主要功能是从输入的编码信号中解码出特定的信息或控制信号。 译码器通常…...

分成sum接近的2个集合,返回相对小的sum
题目描述:给定一个正数数组arr,请把arr中所有的数分成两个集合,尽量让两个集合的累加和接近,返回最接近的情况下,较小集合的累加和sum。 way:选还是不选 //arr[index...]可以自由选择,返回累加和尽量接近…...

SpringBoot前置知识01-SPI接口
SpringBoot前置知识-SPI接口 介绍 Java中SPI是一种服务发现机制,或者说是一种思想,亦是一种约定。其实JDK中的JDBC就是使用了这种用思想,JDBC在JDK中只定义了接口,并没有实现类,连接什么数据库就要引入什么数据库的驱…...
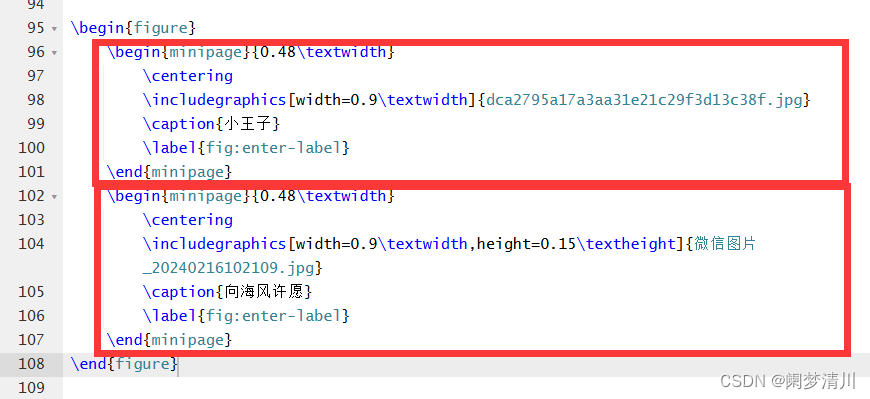
数学建模--LaTeX的基本使用
目录 1.回顾 2.设置这个页眉和页脚 3.对于字体的相关设置 4.对于这个分级标题的设置 5.列表的使用 6.插入图片 1.回顾 (1)昨天我们了解到了这个latex的使用基本常识,以及这个宏包的概念,区域的划分,不同的代码代…...
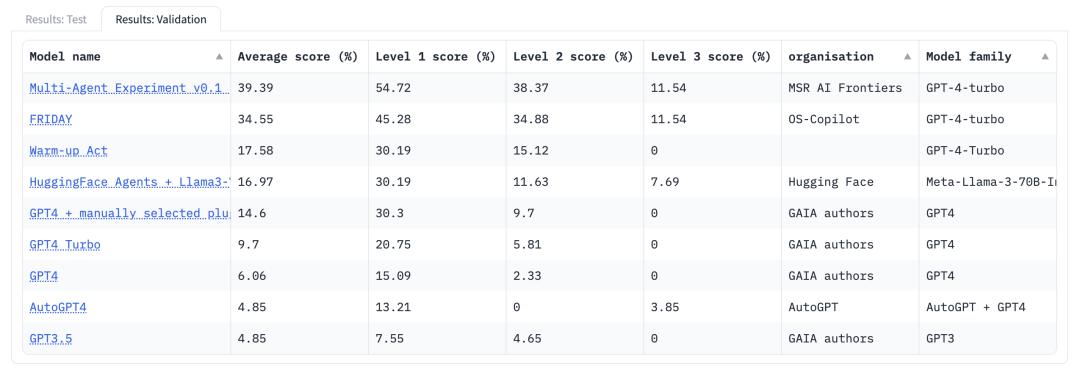
授权调用: 介绍 Transformers 智能体 2.0
简要概述 我们推出了 Transformers 智能体 2.0! ⇒ 🎁 在现有智能体类型的基础上,我们新增了两种能够 根据历史观察解决复杂任务的智能体。 ⇒ 💡 我们致力于让代码 清晰、模块化,并确保最终提示和工具等通用属性透明化…...

流媒体内网穿透/组网/视频协议转换EasyNTS上云网关如何更改密码?
EasyNTS上云网关的主要作用是解决异地视频共享/组网/上云的需求,网页对域名进行添加映射时,添加成功后会生成一个外网访问地址,在浏览器中输入外网访问地址,即可查看内网应用。无需开放端口,EasyNTS上云网关平台会向Ea…...
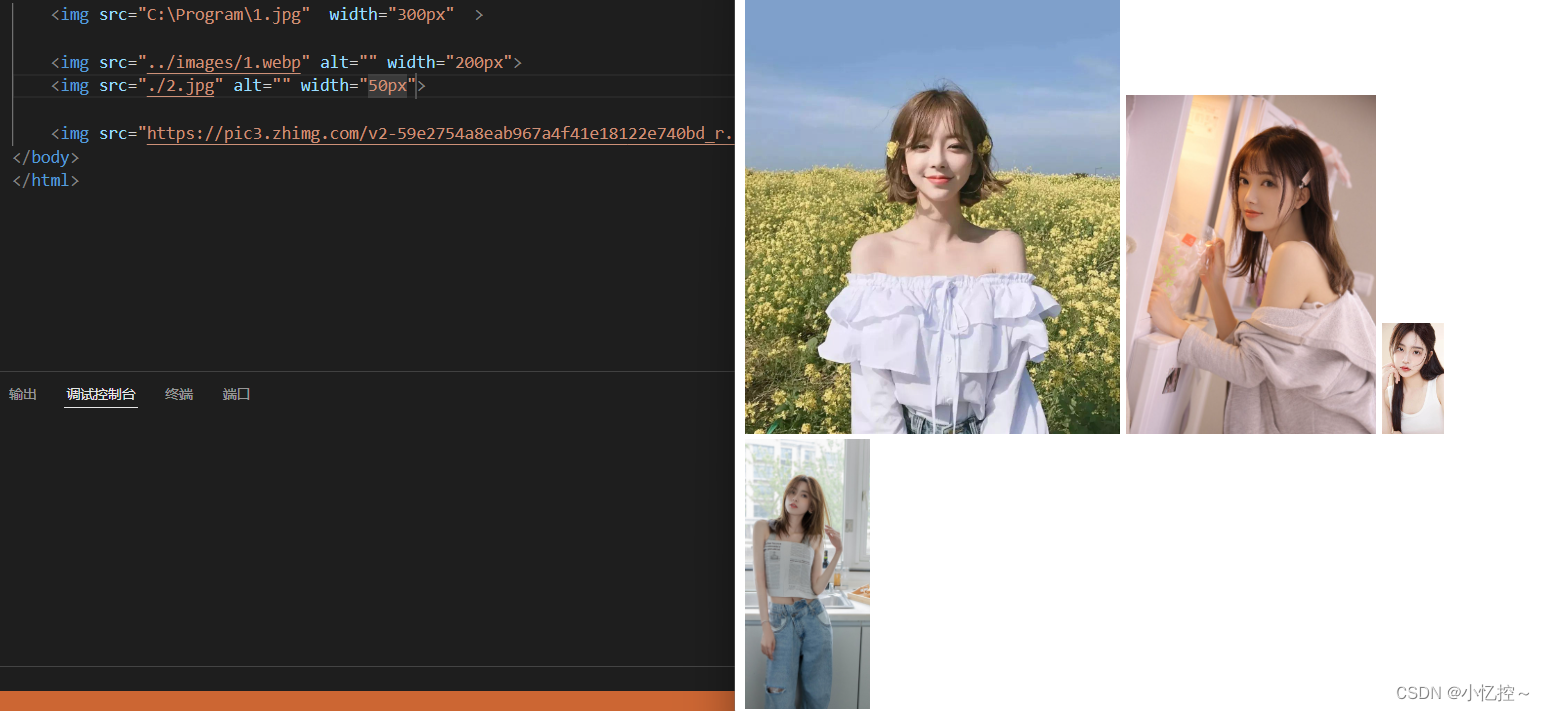
HTML5的标签(文本链接、图片路径详解)
目录 前言 一、文本链接 超链接表述 二、图片路径详解 绝对路径 相对路径 网络路径 前言 一、文本链接 超链接表述 HTML 使用标签<a>来设置超文本链接 超链接可以是一个字,一个词,或者一组词,也可以是一幅图像,…...
(十五))
React Native 之 Linking(链接)(十五)
URL Scheme是什么 URL Scheme是一种机制,主要用于在移动应用程序中打开另一个应用程序或执行特定操作。 定义与原理: URL Scheme允许应用程序通过特定的URL格式与其他应用程序进行交互。 它通过在应用程序中注册一个自定义的URL Scheme,并在…...

Java实现图书系统
首先实现一个图书管理系统,我们要知道有哪些元素? 1.用户分成为管理员和普通用户 2.书:书架 书 3.操作的是: 书架 目录 第一步:建包 第二步:搭建框架 首先:完成book中的方法 其次:完成BookList 然后:完成管理员界面和普通用户界面 最后:Main 第三步:细分方法 1.退…...

Git提交和配置命令
一、提交代码到仓库 在软件开发中,版本控制是一个至关重要的环节。而Git作为目前最流行的版本控制系统之一,为我们提供了便捷高效的代码管理和协作工具。在日常开发中,我们经常需要将本地代码提交到远程仓库,以便于团队协作和版本…...

已解决java.lang.ExceptionInInitializerError: 初始化程序中的异常错误的正确解决方法,亲测有效!!!
已解决java.lang.ExceptionInInitializerError: 初始化程序中的异常错误的正确解决方法,亲测有效!!! 目录 问题分析 报错原因 解决思路 解决方法 分析错误栈信息 检查静态初始化块和静态变量 验证资源和配置 使用日志记录…...

报表显示中,是否具备条件格式功能设计?
**报表显示中确实具备条件格式功能设计**。条件格式是一种根据特定条件对单元格或单元格区域进行格式设置的功能,它可以帮助用户更直观地理解和分析数据。 通过条件格式,用户可以设置多种条件,如单元格值的大小、是否包含特定文本等…...

完全二叉树查找
描述 有一棵树,输出某一深度的所有节点,有则输出这些节点,无则输出EMPTY。该树是完全二叉树。 输入描述 输入有多组数据,遇到0时终止输入。 每组输入一个n(1<n<1000),然后将树中的这n个节点依次输入ÿ…...

Web安全:SQL注入之时间盲注原理+步骤+实战操作
「作者简介」:2022年北京冬奥会网络安全中国代表队,CSDN Top100,就职奇安信多年,以实战工作为基础对安全知识体系进行总结与归纳,著作适用于快速入门的 《网络安全自学教程》,内容涵盖系统安全、信息收集等…...
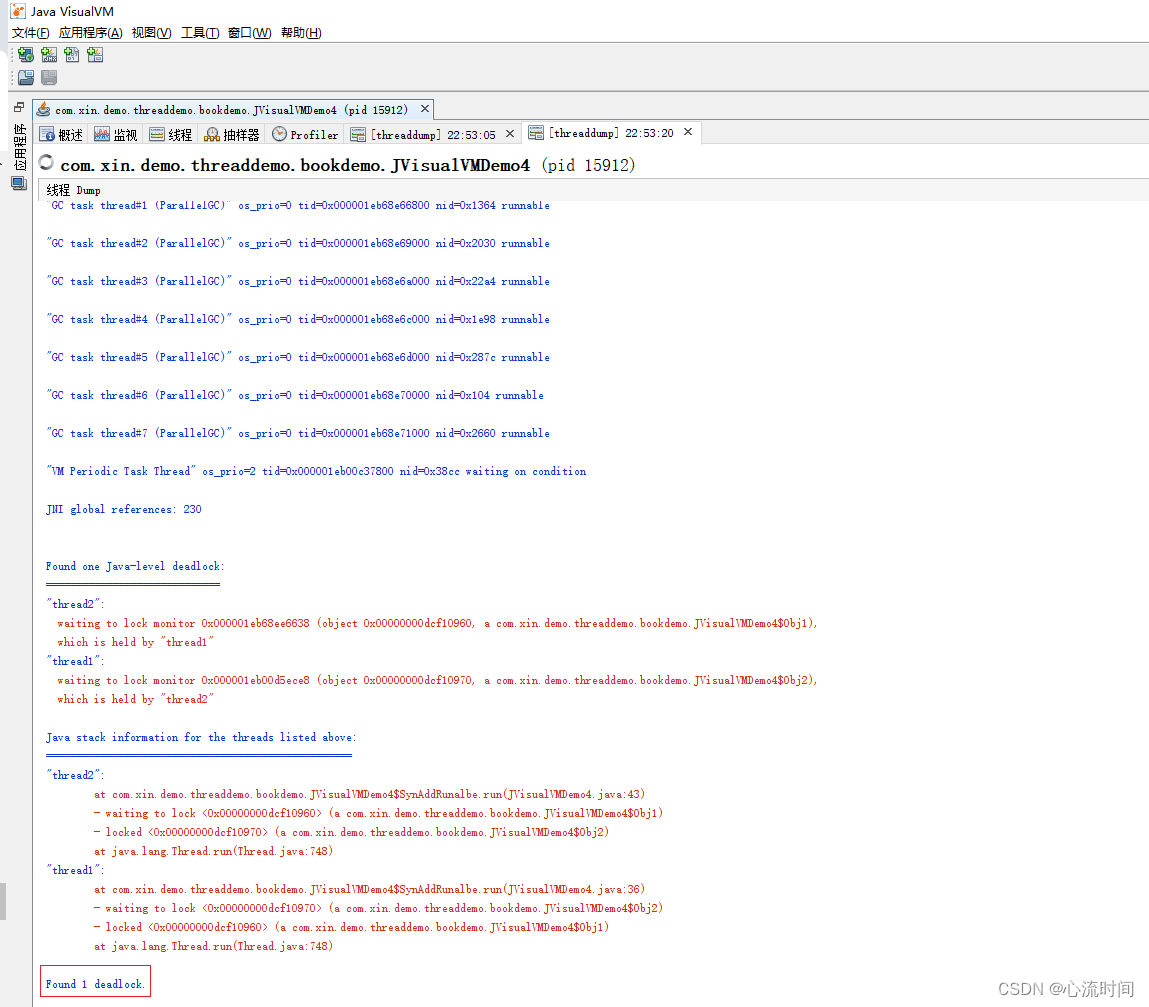
[JDK工具-10] jvisualvm 多合一故障处理工具
文章目录 1. 介绍2. 查看堆的变化3. 查看堆快照4. 导出堆快照文件5. 查看class对象加载信息6. CPU分析:发现cpu使用率最高的方法7. 查看线程快照:发现死锁问题 1. 介绍 VisualVM 是一款免费的,集成了多个 JDK 命令行工具的可视化工具…...
【GateWay】自定义RoutePredicateFactory
需求:对于本次请求的cookie中,如果userType不是vip的身份,不予访问 思路:因为要按照cookie参数进行判断,所以根据官方自带的CookieRoutePredicateFactory进行改造 创建自己的断言类,命名必须符合 xxxRout…...

今日总结2024/5/27
今日学习了状态压缩DP,状态压缩DP分为棋盘型(基于连通性)和集合型 Acwing.1064 小国王 在 nn的棋盘上放 k个国王,国王可攻击相邻的 8个格子,求使它们无法互相攻击的方案总数。 输入格式 共一行,包含两个整数 n和 k。 输出格式 共一行&…...

使用 Snort 进行入侵检测
使用 Snort 进行入侵检测 Snort 是一种流行的开源入侵检测系统。您可以在http://www.snort.org/上获取它。Snort 分析流量并尝试检测和记录可疑活动。Snort 还能够根据其所做的分析发送警报。 Snort 安装 在本课中,我们将从源代码安装。此外,我们不会安…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...

门静脉高压——表现
一、门静脉高压表现 00:01 1. 门静脉构成 00:13 组成结构:由肠系膜上静脉和脾静脉汇合构成,是肝脏血液供应的主要来源。淤血后果:门静脉淤血会同时导致脾静脉和肠系膜上静脉淤血,引发后续系列症状。 2. 脾大和脾功能亢进 00:46 …...
