申办风景园林设计乙级资质如何整理技术人员的专业培训证明
整理技术人员的专业培训证明是申办风景园林设计乙级资质的重要环节,它直接关系到证明技术人员持续学习和专业能力提升的情况。以下是整理专业培训证明的一些建议步骤:
-
收集培训记录:首先,向所有参与设计工作的技术人员收集他们参加过的所有专业培训记录。这些记录包括但不限于培训课程名称、培训机构、培训时间、培训内容概述、培训时长及培训证书等。
-
核对资质要求:根据乙级资质对技术人员的专业培训要求,核对收集到的培训记录是否符合资质标准。注意查看是否有特定类型的培训或一定学时数的要求。
-
分类整理:将所有技术人员的培训证明按人员姓名、职称、培训类别等进行分类整理,便于审阅和提交。可以考虑制作一个详细的表格,列出每个人的培训详情,包括但不限于培训名称、颁发机构、培训日期、培训时数、证书编号等信息。
-
确认证书有效性:确保所有培训证书均为有效期内的正规证书,对于过期或即将过期的证书,需要安排技术人员参加新的培训以更新证书。
-
扫描归档:将所有纸质版的培训证书和相关证明材料扫描成电子版,以便于在提交资质申请时上传或作为附件使用。同时,保留好原件,以备不时之需。
-
附加说明:如果某些培训特别重要或与申请资质直接相关,可以在整理的文档中附加简短说明,强调这些培训对提升技术人员专业技能的作用。
-
审核与校对:在提交前,由专人负责对所有培训记录进行细致审核,确保信息的准确无误,避免错漏或重复。
-
按要求格式提交:最后,根据资质申请的具体要求,将整理好的培训证明材料按照指定的格式(如PDF、Word文档等)和顺序排列,准备好与其他申请材料一起提交。
整个过程中,保持与资质审批部门的良好沟通,及时了解是否有特定的格式或提交要求,确保提交的材料符合最新的规定和要求。如需详细咨询,请随时联系河南宽信刘工。
相关文章:

申办风景园林设计乙级资质如何整理技术人员的专业培训证明
整理技术人员的专业培训证明是申办风景园林设计乙级资质的重要环节,它直接关系到证明技术人员持续学习和专业能力提升的情况。以下是整理专业培训证明的一些建议步骤: 收集培训记录:首先,向所有参与设计工作的技术人员收集他们参加…...
类别型特征
#机器学习 #深度学习 #基础知识 #特征工程 #数据编码 背景 在现实生活中,我们面对的数据类型有很多,其中有的数据天然为数值类型具备数值意义,那么可以很自然地和算法结合,但是大部分数据他没有天然的数值意义,那么将他们送入到算法前,就需要对数据进行编码处理,将其转换为数…...

java医院管理系统源码(springboot+vue+mysql)
风定落花生,歌声逐流水,大家好我是风歌,混迹在java圈的辛苦码农。今天要和大家聊的是一款基于springboot的医院管理系统。项目源码以及部署相关请联系风歌,文末附上联系信息 。 项目简介: 医院管理系统的主要使用者分…...

vue2 面试题
一、.vue的性能优化怎么做? 1.编码优化: 不要把所有的数据都放在data中;v-for时给每个元素绑定事件用事件代理;keep-alive缓存组件;尽可能拆分组件,提高复用性、维护性;key值要保证唯一&#…...

【JavaEE精炼宝库】多线程(3)线程安全 | synchronized
目录 一、线程安全 1.1 经典线程不安全案例: 1.2 线程安全的概念: 1.3 线程不安全的原因: 1.3.1 案例刨析: 1.3.2 线程不安全的名词解释: 1.3.3 Java 内存模型 (JMM): 1.3.4 解决线程不安全问题: 二…...
el-table-column两种方法处理特殊字段,插槽和函数
问题:后端返回的字段为数字 解决办法: {{ row[item.prop] 1 ? "启用" : "禁用" }} {{ row[item.prop] }} 最终果: 另外:如果多种状态时可用函数 {{ getStatus(row[item.prop]) }} {{ row[item.prop…...
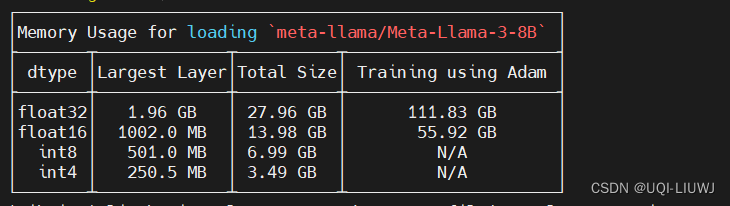
huggingface笔记: accelerate estimate-memory 命令
探索可用于某一机器的潜在模型时,了解模型的大小以及它是否适合当前显卡的内存是一个非常复杂的问题。为了缓解这个问题,Accelerate 提供了一个 命令行命令 accelerate estimate-memory。 accelerate estimate-memory {MODEL_NAME} --library_name {LIBR…...

李飞飞亲自撰文:大模型不存在主观感觉能力,多少亿参数都不行
近日,李飞飞连同斯坦福大学以人为本人工智能研究所 HAI 联合主任 John Etchemendy 教授联合撰写了一篇文章,文章对 AI 到底有没有感觉能力(sentient)进行了深入探讨。 「空间智能是人工智能拼图中的关键一环。」知名「AI 教母」李…...

超级好用的C++实用库之套接字
💡 需要该C实用库源码的大佬们,可搜索微信公众号“希望睿智”。添加关注后,输入消息“超级好用的C实用库”,即可获得源码的下载链接。 概述 C中的Socket编程是实现网络通信的基础,允许程序通过网络与其他程序交换数据。…...
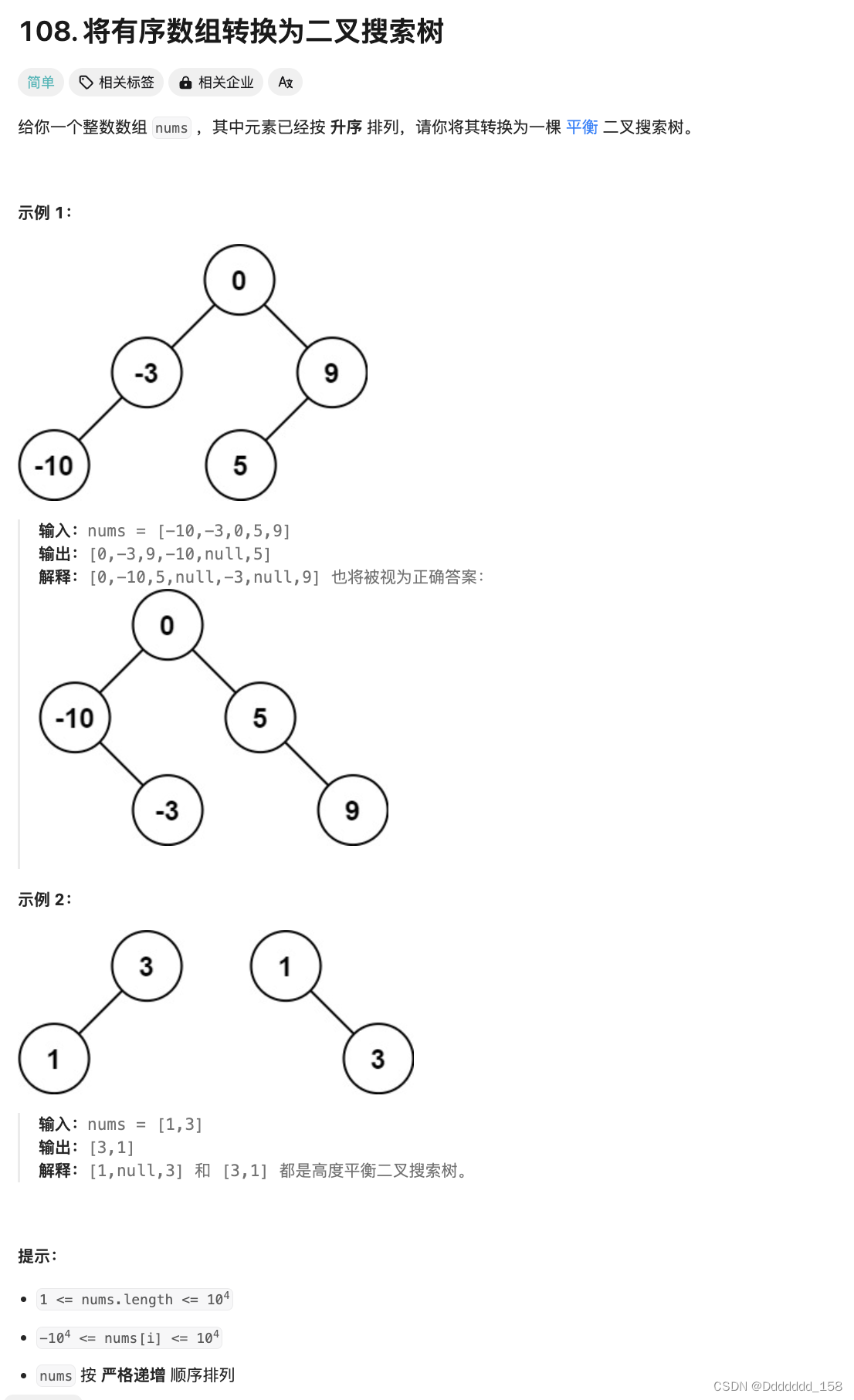
C++ | Leetcode C++题解之第108题将有序数组转换为二叉搜索树
题目: 题解: class Solution { public:TreeNode* sortedArrayToBST(vector<int>& nums) {return helper(nums, 0, nums.size() - 1);}TreeNode* helper(vector<int>& nums, int left, int right) {if (left > right) {return nu…...

5月27日,每日信息差
第一、韩国宇宙航空厅于 5 月 27 日正式成立,旨在推动以民间为主的太空产业生态圈发展,助力韩国成为航天强国。首任厅长尹宁彬表示,该机构将在庆尚南道泗川市的临时大楼开展相关工作。 第二、京东集团宣布,自2024年7月1日起&…...

echart扩展插件词云echarts-wordcloud
echart扩展插件词云echarts-wordcloud 一、效果图二、主要代码 一、效果图 二、主要代码 // 安装插件 npm i echarts-wordcloud -Simport * as echarts from echarts; import echarts-wordcloud; //下载插件echarts-wordcloud import wordcloudBg from /components/wordcloudB…...

解决无法直接抓取链接地址
当我们在爬取一些文章列表的时候,可能无法从接口或者html界面上获取到文章的详细列表 这个时候我们可以通过模拟点击且重写window.open方法,将跳转的地址捕获,并且放到html中去。 这样我们就可以获取到某个文章的详细地址了 // 保存原始的 …...

java面对对象编程-多态
介绍 方法的多态 多态是在继承,重载,重写的基础上实现的 我们可以看看这个代码 package b;public class main_ {public static void main(String[] args) { // graduate granew graduate(); // gra.cry();//这个时候,子类的cry方法就重写…...
【Sql Server】随机查询一条表记录,并重重温回顾下自定义函数的封装和使用
大家好,我是全栈小5,欢迎来到《小5讲堂》。 这是《Sql Server》系列文章,每篇文章将以博主理解的角度展开讲解。 温馨提示:博主能力有限,理解水平有限,若有不对之处望指正! 目录 前言随机查询语…...

基于C#开发web网页管理系统模板流程-主界面管理员录入和编辑功能完善
前言 紧接上篇->基于C#开发web网页管理系统模板流程-登录界面和主界面_c#的网页编程-CSDN博客 已经完成了登录界面和主界面,本篇将完善主界面的管理员录入和编辑功能,事实上管理员录入和编辑的设计套路适用于所有静态表的录入和编辑 首先还是介绍一下…...

K8s证书过期处理
问题描述 本地有一个1master2worker的k8s集群,今天启动VMware虚拟机之后发现api-server没有起来,docker一直退出,这个集群是使用kubeadm安装的。 于是kubectl logs查看了日志,发现证书过期了 解决方案: 查看证书 #…...
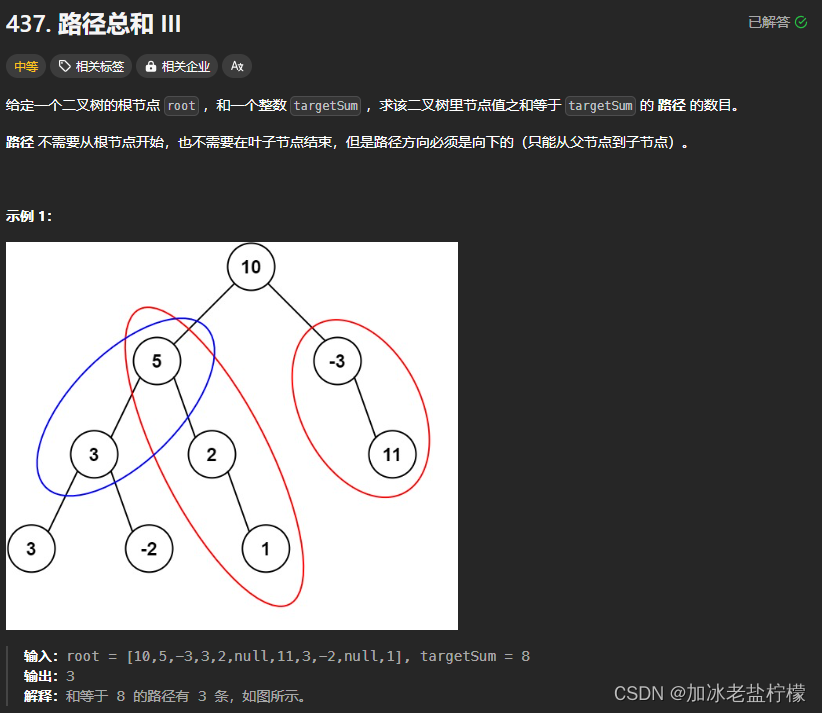
刷题之路径总和Ⅲ(leetcode)
路径总和Ⅲ 这题和和《为K的数组》思路一致,也是用前缀表。 代码调试过,所以还加一部分用前序遍历数组和中序遍历数组构造二叉树的代码。 #include<vector> #include<unordered_map> #include<iostream> using namespace std; //Def…...

MongoDB 原子操作:确保数据一致性和完整性的关键
在 MongoDB 中,原子操作是指可以一次性、不可分割地执行的数据库操作。这些操作能够保证在多个并发操作中不会出现数据不一致或者丢失的情况,确保数据库的数据完整性和一致性。 基本语法 MongoDB 的原子操作通常与更新操作相关,其基本语法如…...

2024上半年软考高级系统架构设计师回顾
本博客地址:https://security.blog.csdn.net/article/details/139238685 2024年上半年软考在5月25-26日举行,趁着时间刚过去记忆还在,简单写一点总结。 关于考试形式:上机考试(以后也都是机考)࿰…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...
