24年gdcpc省赛C题

1279:DFS 序

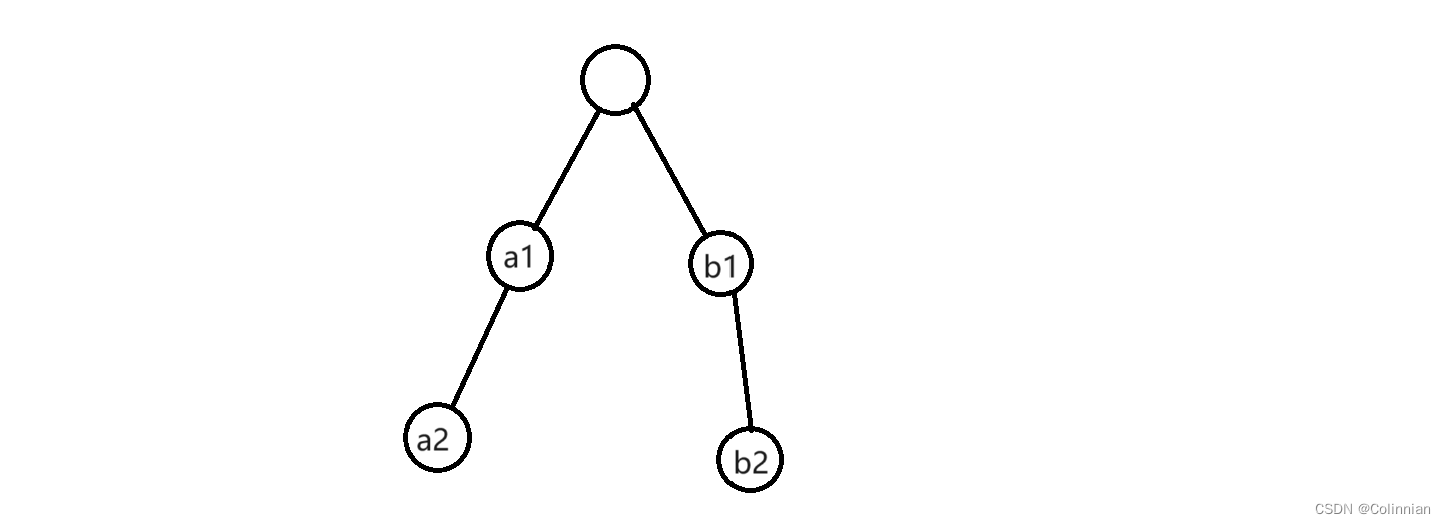
先不考虑多节点,先看着颗二叉树,假设他们的父亲节点是第k个被访问的点,如果先访问左子树,那么得到的结果是a1*k+a2*(k+1)+b1*(2+k)+b2*(2+k+1),可以发现,先访问左子树,那么右子树每次的乘以的p值实际上是左子树乘以的p值加上左子树的节点个数,比如a1*k和b1*(2+k),如果不看2,它们同样是第k个被访问的,先访问了a子树,而a子树的节点个数是2,所以再次访问b子树的时候,每一个b子树的节点都加上了2.

那么先访问a子树使得b子树多增加的权值是a子树的节点个数*b子树的权值之和.,同理,先访问b子树那么增加的权值之和是a子树的权值乘以b子树的节点,所以只需要判断是suma*nodeb和sumb*nodea哪一个更大即可.

代码如下

using ll = long long;
struct node {ll num;ll sum;ll node;
};int main() {int n;std::cin >> n;std::vector<node>w(n + 1);for (int i = 1; i <= n; i++) {std::cin >> w[i].sum;w[i].num = w[i].sum;w[i].node = 1;}std::vector<std::vector<ll>>adj(n+1);for (int i = 2; i <= n; i++) {int x;std::cin >> x;adj[x].push_back(i);}auto dfs = [&](auto self,int p)->void {//叶子节点返回if (adj[p].empty())return;//非叶子节点遍历,并累加权值for (auto q : adj[p]) {self(self, q);w[p].sum += w[q].sum;w[p].node += w[q].node;}//排序//sumx*nodey表示先走y,再走x,sumy*nodex,如果先访问y增加的权值大于先访问x增加的权值,那么表达式返回false,交换x,y;std::sort(adj[p].begin(), adj[p].end(), [&](ll x, ll y) {return w[x].sum * w[y].node < w[y].sum * w[x].node;});};dfs(dfs, 1);ll ans = 0,cnt=0;auto bfs = [&](auto self, int p)->void {ans += ++cnt * w[p].num;if (adj[p].empty())return;for (auto q : adj[p]) {self(self, q);}};bfs(bfs, 1);std::cout << ans << '\n';return 0;
}