深入理解二叉树及其在C语言中的实现
一、引言
二叉树是数据结构中一种非常基础且重要的树形结构,它的每个节点最多有两个子节点,通常被称为左子节点和右子节点。二叉树在计算机科学中有着广泛的应用,如搜索、排序、存储数据等。本文将详细介绍二叉树的基本概念、特性以及在C语言中的实现方式。
二、二叉树的基本概念
- 节点:二叉树的基本单元,包含数据域和指向左右子节点的指针。
- 根节点:没有父节点的节点,是二叉树的起点。
- 叶子节点:没有子节点的节点,是二叉树的终点。
- 度:一个节点拥有的子节点数。二叉树的度最大为2。
- 深度(或高度):从根节点到最远叶子节点的最长路径上的节点数。
三、二叉树的特性
- 递归性:二叉树的左子树和右子树也是二叉树。
- 有序性:二叉树的左子树和右子树是严格区分的,不能随意颠倒。
四、二叉树在C语言中的实现
下面是一个简单的二叉树节点的C语言结构体定义:
#include <stdio.h>
#include <stdlib.h>
// 定义二叉树节点结构体
typedef struct TreeNode
{
int val; // 节点值
struct TreeNode *left; // 左子节点指针
struct TreeNode *right; // 右子节点指针
} TreeNode;接下来,我们可以创建一些基本的二叉树操作函数,如插入节点、遍历二叉树等。以下是一个简单的二叉树遍历示例(前序遍历):
// 前序遍历(根-左-右)
void preOrderTraversal(TreeNode *root)
{ if (root == NULL) { return; } printf("%d ", root->val); // 访问根节点 preOrderTraversal(root->left); // 遍历左子树 preOrderTraversal(root->right); // 遍历右子树
}为了完整性,我们还可以添加中序遍历(左-根-右)和后序遍历(左-右-根)的代码:
// 中序遍历(左-根-右)
void inOrderTraversal(TreeNode *root)
{ if (root == NULL) { return; } inOrderTraversal(root->left); // 遍历左子树 printf("%d ", root->val); // 访问根节点 inOrderTraversal(root->right); // 遍历右子树 } // 后序遍历(左-右-根)
void postOrderTraversal(TreeNode *root)
{ if (root == NULL) { return; } postOrderTraversal(root->left); // 遍历左子树 postOrderTraversal(root->right); // 遍历右子树 printf("%d ", root->val); // 访问根节点
}五、总结
本文介绍了二叉树的基本概念、特性以及在C语言中的实现方式。通过定义二叉树节点的结构体,我们可以轻松地实现二叉树的插入、遍历等操作。二叉树作为数据结构的重要组成部分,对于理解树形结构、递归算法等方面都有着重要意义。希望本文能够帮助读者更好地掌握二叉树的相关知识。
相关文章:

深入理解二叉树及其在C语言中的实现
一、引言 二叉树是数据结构中一种非常基础且重要的树形结构,它的每个节点最多有两个子节点,通常被称为左子节点和右子节点。二叉树在计算机科学中有着广泛的应用,如搜索、排序、存储数据等。本文将详细介绍二叉树的基本概念、特性以及在C语言…...

基于ssm+vue图书管理系统
基于ssmvue图书管理系统 ssm477图书管理系统 相关技术 javassmmysqlvueelementui...

高防ip能防护变异CC攻击吗
高防ip能防护变异CC攻击吗?随着互联网的不断发展,网络安全问题也日益突出,各类网络攻击层出不穷,其中CC攻击(Challenge Collapsar攻击)及其变种——变异CC攻击,更是让众多企业和个人网站头疼不已…...
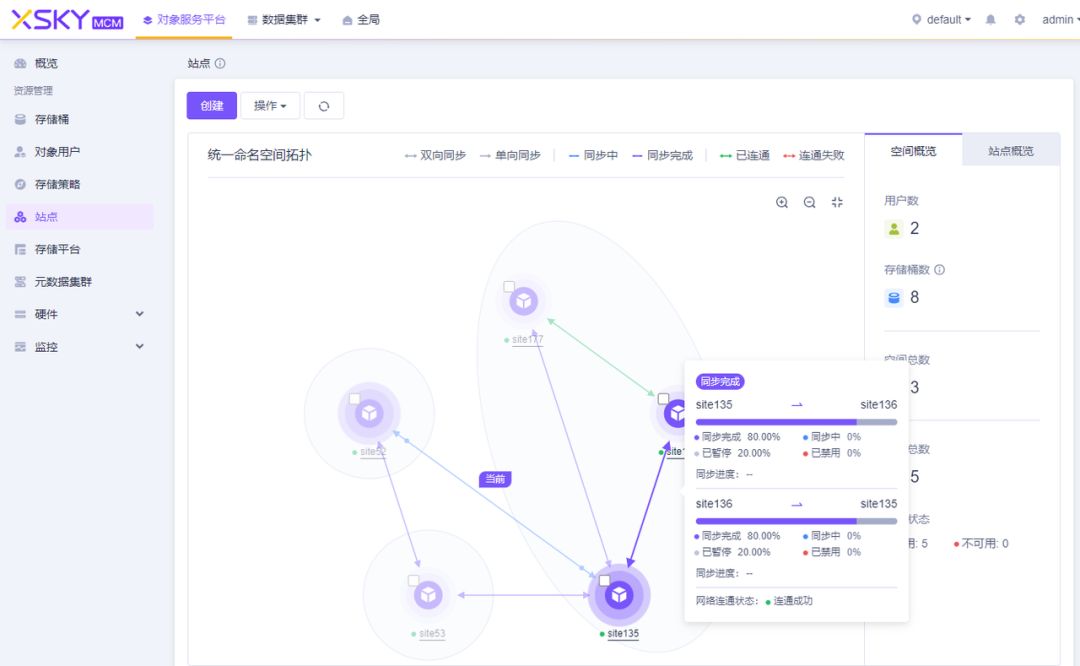
从多站点到多活,XEOS 对象数据容灾能力再提升
近日, XSKY SDS V6.4 新版本发布,其中 XEOS V6.4 全新升级并完善了统一命名空间功能,更进一步增强和完善了异地容灾方案,配合强一致代理读,可以实现异地多活;同时大幅降低管理复杂度,有效降低容…...
3D开发工具HOOPS在BIM系统中的应用
建筑信息模型是一种革命性的建筑设计、施工和管理方法。它通过创建和利用数字信息来优化建筑项目的设计、施工和运营过程。在这个过程中,3D开发工具HOOPS扮演着至关重要的角色,为BIM系统提供了强大的技术支持和丰富的功能。HOOPS中文网http://techsoft3d…...

适合下班做的副业兼职、1天挣300,7天涨粉2万
最近小红书上有类视频火了! 周周近财:让网络小白少花冤枉钱,赚取第一桶金 利用AI制作的漫画解说历史小说视频。视频以《明朝那些事儿》为蓝本,一上线就疯狂吸粉,多条视频内容都大爆了。 就是这个账号,仅仅…...

JS中getElementById与querySelector区别收录
JS中getElementById与querySelector区别收录 getElementById 和 querySelector 都是 JavaScript 中用于从文档中选取元素的方法,但两者之间存在一些关键区别: 选择器语法: getElementById:这个方法只接受一个参数,即元…...

Android:使用Kotlin搭建MVC架构模式
一、简介Android MVC架构模式 M 层 model ,负责处理数据,例如网络请求、数据变化 V 层 对应的是布局 C 层 Controller, 对应的是Activity,处理业务逻辑,包含V层的事情,还会做其他的事情,导致 ac…...

delete原理
一 原理 new申请动态内存,delete释放内存,将内存的数据块标记为可覆盖,可再次使用。在调用delete时不会将内存块的数据,全部初始化为0。 二 new动态内存,不调用delete的后果? 造成内存泄漏。new申请的动…...

青少年 CTF 练习平台:Misc(一)
前言 当然,我可以更详细地介绍一下青少年CTF练习平台。 青少年CTF练习平台是一个专为青少年设计的网络安全竞赛和训练平台。该平台由思而听(山东)网络科技有限公司与克拉玛依市思而听网络科技有限公司共同建设,自2018年创建以来…...

展锐平台+Android系统开发概要
文章目录 一、缩略语二、系统分区1. UIS7885android13的系统分区 三、系统编译四、开发调试 一、缩略语 BBAT:Baseband Auto Test,基带自带测试CRC:Cyclic Redundancy Check,循环冗余检验SPL:Secondary Program Loade…...
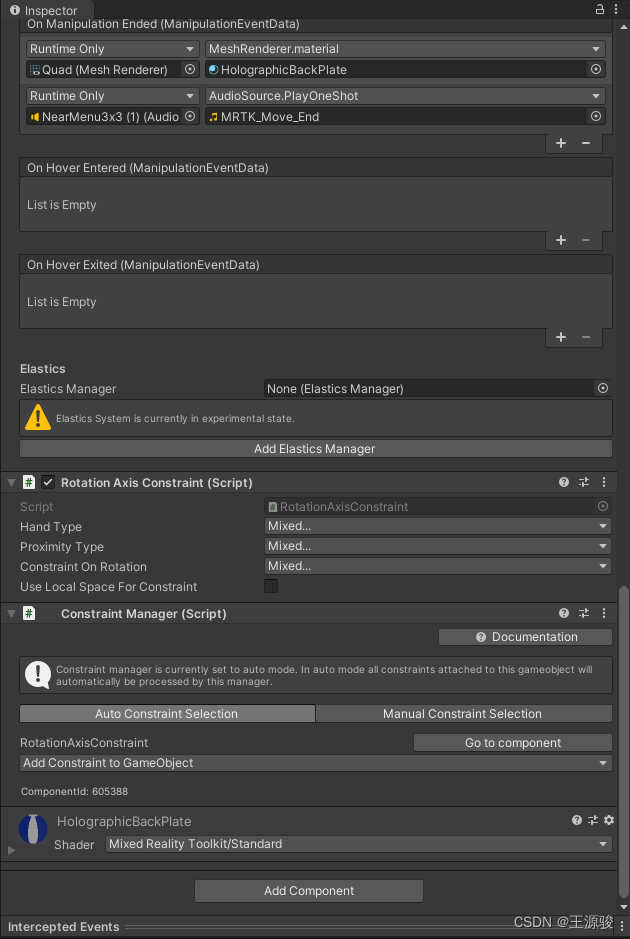
unity开发Hololens 制作滑动框
一定要做到最后一步,才会有效果 1、创建空物体 ,并添加组件 创建空物体 命名ScrollingObjectCollection, 添加组件如下图 下面是各个组件展开的内容 2、在ScrollingObjectCollection 下面创建两个空物体,分别命名Container、Clipping…...

【JavaEE进阶】——Spring Web MVC (响应)
目录 🚩学习Spring MVC 🎈返回静态网页 🎈返回数据ResponseBody 🎈返回html代码片段 🎈返回JSON 🎈设置状态码 🎈设置Header 🚩学习Spring MVC 既然是 Web 框架, 那么当⽤⼾在…...
基于springboot+vue的公司资产网站(全套)
一、系统架构 前端:vue2 | element-ui 后端:springboot | mybatis 环境:jdk1.8 | mysql | maven | node 二、代码及数据库 三、功能介绍 01. 管理后台-登录 02. 管理后台-首页 03. 管理后台-个人中心-修改密码 04. 管理后台-个人…...

Element-UI10分钟快速入门
Element-UI 是一个基于 Vue.js 的桌面端组件库,它为开发者提供了一套完整、易用、美观的组件解决方案,极大地提升了前端开发的效率和质量。以下是一个 Element-UI 的快速入门指南: 1. 安装 Element-UI 首先,确保你已经创建了一个…...

深入解析:如何在遍历List时安全地删除元素
什么是并发修改异常(ConcurrentModificationException) 在深入探讨解决方案之前,我们首先要理解什么是并发修改异常。当我们使用迭代器(Iterator)遍历一个List时,如果在迭代过程中结构被修改(比…...
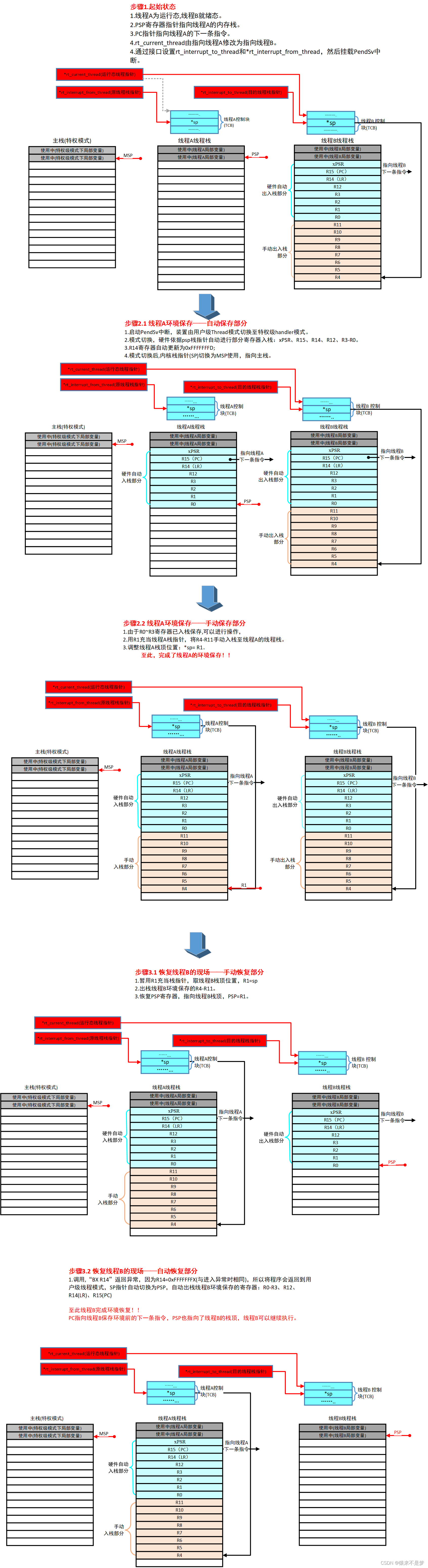
RT_Thread内核源码分析(一)——CM3内核和上下文切换
目录 一、程序存储分析 1.1 CM3内核寻址空间映射 1.2 程序静态存储和动态执行 二、CM3内核相关知识 2.1 操作模式和特权极别 2.2 环境相关寄存器 2.2.1 通用寄存器组, 2.2.2 状态寄存器组 2.2.3 模式切换环境自动保存 2.2.4 函数调用形参位置 2.3 …...

Android 13 高通设备热点低功耗模式
需求: Android设备开启热点,使Iphone设备连接,自动开启低数据模式 低数据模式: 低数据模式是一种在移动网络或Wi-Fi环境下,通过限制应用程序的数据使用、降低数据传输速率或禁用某些后台操作来减少数据流量消耗的优化模式。 这种模式主要用于节省数据流量费用,特别是…...
律所电子签章有效吗,怎么操作?
电子签章在很多国家和地区是合法有效的,但其有效性、使用条件和操作流程可能依据具体的法律法规而有所不同。在中国,随着《中华人民共和国电子签名法》的实施,电子签章在满足一定条件下是具有法律效力的。电子签章可以提高合同签订的效率&…...

详解 Scala 的变量、标识符、数据类型
一、注释 Scala 注释与 Java 一致 // 单行注释/** 多行注释*//*** 文档注释*/二、变量与常量 1. 语法 // 变量,类型可以省略 var varName:varClass value // 常量,类型可以省略 val valName:valClass value2. 案例 // 使用 var/val 才会在类中声明属…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...
