Easy Deep Learning——PyTorch中的自动微分
目录
什么是深度学习?它的实现原理是怎么样的呢?
什么是梯度下降?梯度下降是怎么计算出最优解的?
什么是导数?求导对于深度学习来说有何意义?
PyTorch 自动微分(自动求导)
为什么选择这一章作为第一章而不是介绍深度学习的核心数据结构张量呢?原因在于张量运算实际就是矩阵的运算,另外PyTorch关于张量的数据处理函数很多,没必要逐个介绍,用到的时候去查文档即可,介绍过多张量的计算方式其实并无意义。
在入门深度学习时,我相信初学者最关心的是什么是深度学习?它的基本原理是怎么样的,而不是上来就列一大堆代数式,然后去进行各种数据计算。现在,读者只需要知道“张量”是PyTorch中最基本的数据结构,它是一个数组,如果要说的再清楚些,可以这样描述
在 PyTorch 中,张量(Tensor)是最基本的数据结构,是实现各种模型和算法的基础,类似于 NumPy 中的数组。它可以用来表示数字、向量、矩阵、张量等各种数据形式,同时支持 GPU 计算加速。
张量可以有不同的维度,分别是标量(0 维)、向量(1 维)、矩阵(2 维)和高维张量(3 维或更多维)。除了维度外,每个张量还有一个数据类型(如 float、int、bool 等)和一个设备类型(CPU 或 GPU)。
那么现在回到我们最关心的话题
什么是深度学习?它的实现原理是怎么样的呢?
深度学习的原理是让计算机学会从数据中提取特征,并用这些特征来解决问题。与传统的计算机程序不同,深度学习模型不需要人为地设计特征提取方式,而是让计算机自动学习。这个过程类似于人类学习语言或者乐器,我们不需要事先学会所有的单词或者音符,而是从语境或者旋律中提取出有用的信息,慢慢地积累经验并改进自己。
具体来说,深度学习模型是由神经网络组成的,每个神经元负责接收一些输入并产生一些输出。这些输入和输出可以被看做是特征的不同表示方式,例如对于图像数据,可以把像素值作为输入,然后每个神经元输出的是对应的图像特征。为了让神经网络自动学习到有用的特征,我们需要为它提供大量的数据,并让它通过反向传播算法不断调整自己的参数。
反向传播算法的基本思路是利用导数信息,从输出端反向推导神经网络中每个参数的贡献度,并根据这个贡献度来调整参数,从而让模型的预测结果更加准确。这个过程类似于一个小孩子学习画画,一开始可能会画得很丑,但是每次被告知错误的地方,就能不断改进,最终画出漂亮的图画。
总的来说,深度学习的原理是通过神经网络自动学习数据中的特征,利用反向传播算法来不断优化模型参数,从而使模型的预测结果更加准确。
说的再通俗点,可以这样描述:
深度学习就是从数据中提取特征,找到特征的规律,来得出结果。这个规律是一个函数,数据是函数的自变量,而结果就是函数的因变量。其中的规律则是函数的权重和偏置,深度学习就是通过大量的数据来求得函数的权重从而得到正确结果的。而一般数据非常复杂影响结果的自变量很多,于是这些函数组成了一个非常复杂的函数组(神经网络)。举个简单的例子
假设一个机器要学习的函数是 : y = kx + b
此时只需要两组数据 ,例如 (1,5)( 2,7),即可求得k,b
于是求得函数表达式为 y = 2x+3 ,这个计算 k,b的过程称为 “学习”。
此时输入一个陌生的自变量,比如 3,此时机器通过两组数据进行“学习”之后,得到了函数的表达式,因此,机器将 3 代入表达式就可以得出正确结果为 9
然而如此简单的函数模型是无法匹配现实中非常复杂的问题的,那么对于非常复杂的函数,机器是怎么计算其中的 k 和 b的呢?
上面已经介绍了反向传播方法,就是从结果的好坏去纠正模型的参数,反向来优化得出结果。
下面介绍深度学习的算法基石:梯度下降算法
什么是梯度下降,梯度下降是怎么计算出最优解的?
假设你在爬山,想要到达山顶。你的目标是走到山顶,但是你并不知道应该往哪个方向走才能最快到达山顶。你的手头有一张地图,上面有你所在的位置和山的形状。
这时候,你可以利用梯度的信息来找到最快到达山顶的方向。梯度是指函数变化最快的方向,你可以把它想象成地图上高度变化最快的地方,就像一个“斜坡”的方向。
通过不断地朝着梯度的方向走,你就可以越来越接近山顶。每次走的步子大小可以通过学习率来控制,学习率越大,走的步子就越大,但是可能会“越过”山顶而错过最优解;学习率越小,走的步子就越小,但是需要更多的步数才能到达最优解。
在深度学习中,我们的目标是最小化损失函数,找到最优解。梯度下降就是一种常用的优化算法,通过不断地计算损失函数关于参数的梯度,朝着梯度的方向调整参数,使得损失函数不断减小,最终找到最优解。
接下来可能读者又会产生一个问题:计算机是怎么找到山谷高度变化最快的方向,然后沿着这个方向找答案的呢?
答案是导数。我们都知道导数表示函数在某一点上的变化率,因此导数就可以帮助我们找到函数的
最快的方向,
什么是导数?求导对于深度学习来说有何意义?
导数是微积分中的概念,表示函数在某一点上的变化率或斜率。在机器学习和深度学习中,导数(或者更一般地说,梯度(可以理解为山谷的斜坡高度))具有至关重要的作用。
首先,导数可以帮助我们找到函数的极值点(最大值或最小值)。在深度学习中,我们通常会用损失函数(每上一个台阶,距离山顶高度最优的直线距离的偏差,就是你要多走的路,在函数中定义为损失)来衡量模型的预测与真实值之间的误差,我们的目标就是最小化这个损失函数。通过计算损失函数关于模型参数的导数,我们可以找到使得损失函数最小化的参数值,从而优化模型。
其次,导数可以帮助我们理解函数的变化规律,例如函数的单调性和凸凹性。在深度学习中,我们通常会通过观察损失函数随着模型参数的变化趋势来判断模型的训练情况和性能。
如此复杂的函数模型,如果让我们手动求导显然工作量太大了。那么有了上面的理解,引入本节知识点——自动微分。
最后,自动微分(或者说自动求导)是深度学习中非常重要的技术之一,可以帮助我们自动地计算复杂模型中的导数,从而方便模型的优化。
PyTorch深度学习框架都提供了自动微分功能,可以大大简化模型开发过程中的计算难度和计算量。
PyTorch自动微分(自动求导)
PyTorch中的自动微分(自动求导)主要通过torch.autograd模块来实现。其中,最常用的函数是torch.Tensor.backward(),它可以自动计算张量的梯度(梯度就是导数值),并将结果存储在grad属性中。在计算张量的导数之前,需要设置该张量可导,requires_grad=True
举一个简单的例子,假设我们有一个函数y = 2x^2 + 3x + 1,可以通过以下代码实现它的自动微分:
import torchx = torch.tensor(2.0, requires_grad=True) # 定义张量x,并开启梯度追踪 y = 2 * x**2 + 3 * x + 1y.backward() # 自动计算y对x的梯度print(x.grad) # 输出梯度
输出的结果为11。我们手动验证下:
y = 2x^2 + 3x + 1 的导数为 y = 4x +3,x=2 代入 得:
y = 4 * 2 + 3 = 11
验证正确。
下面再举一个例子
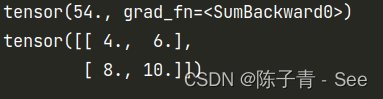
import torchx = torch.tensor([[1.0,2.0],[3.0,4.0]],requires_grad = True)y = torch.sum(x**2+2*x+1) #sum函数:将x的每一个值带入表达式的值,然后求和 print(y) # 54 = 4 + 9 + 16 + 25 y.backward() # 求解y关于x的导数 print(x.grad)
验证如下:
y = x^2+ 2*x +1 求导为 y = 2x +2
将 1 ,2,3,4 代入得
4,6,8,10
验证正确
相关文章:
Easy Deep Learning——PyTorch中的自动微分
目录 什么是深度学习?它的实现原理是怎么样的呢? 什么是梯度下降?梯度下降是怎么计算出最优解的? 什么是导数?求导对于深度学习来说有何意义? PyTorch 自动微分(自动求导) 为什么…...

【生物信息】利用ChatGPT解释GO分析中的关于Biological Processes的问题
利用ChatGPT解释GO分析中的一些问题 如何理解GO中的evidence:ISS,这是什么?qualifier:involved_in是什么意思?evidence:TAS是什么?evidence: IBA是什么?evidence: IMP是什么?evidence:IDA是什么?evidence: IEA是什么?GO分析中,evidence: NAS是什么意思?GO分析中…...

2018年MathorCup数学建模C题陆基导弹打击航母的数学建模与算法设计解题全过程文档及程序
2018年第八届MathorCup高校数学建模挑战赛 C题 陆基导弹打击航母的数学建模与算法设计 原题再现: 火箭军是保卫海疆主权的战略力量,导弹是国之利器。保家卫国,匹夫有责。为此,请参赛者认真阅读"陆基反舰导弹打击航母的建模示意图"。(附图 1 )参考图中的…...
打怪升级之CFile类
CFile类 信息源自官方文档:https://learn.microsoft.com/zh-cn/cpp/mfc/reference/cfile-class?viewmsvc-170。 CFile是Microsoft 基础类文件类的基类。它直接提供非缓冲的二进制磁盘输入/输出设备,并直接地通过派生类支持文本文件和内存文件。CFile与…...

[css]通过网站实例学习以最简单的方式构造三元素布局
文章目录二元素布局纵向布局横向布局三元素布局b站直播布局实例左右-下 布局左-上下 布局上下-右 布局方案一方案二后言二元素布局 在学习三元素布局之前,让我们先简单了解一下只有两个元素的布局吧 两个元素的相对关系非常简单,不是上下就是左右 纵向布…...
【冲刺蓝桥杯的最后30天】day6
大家好😃,我是想要慢慢变得优秀的向阳🌞同学👨💻,断更了整整一年,又开始恢复CSDN更新,从今天开始更新备战蓝桥30天系列,一共30天,如果对你有帮助或者正在备…...
ssm框架之spring:浅聊IOC
IOC 前面体验了spring,不过其运用了IOC,至于IOC( Inverse Of Controll—控制反转 ) 看一下百度百科解释: 控制反转(Inversion of Control,缩写为IoC),是面向对象编程中的一种设计原则&#x…...
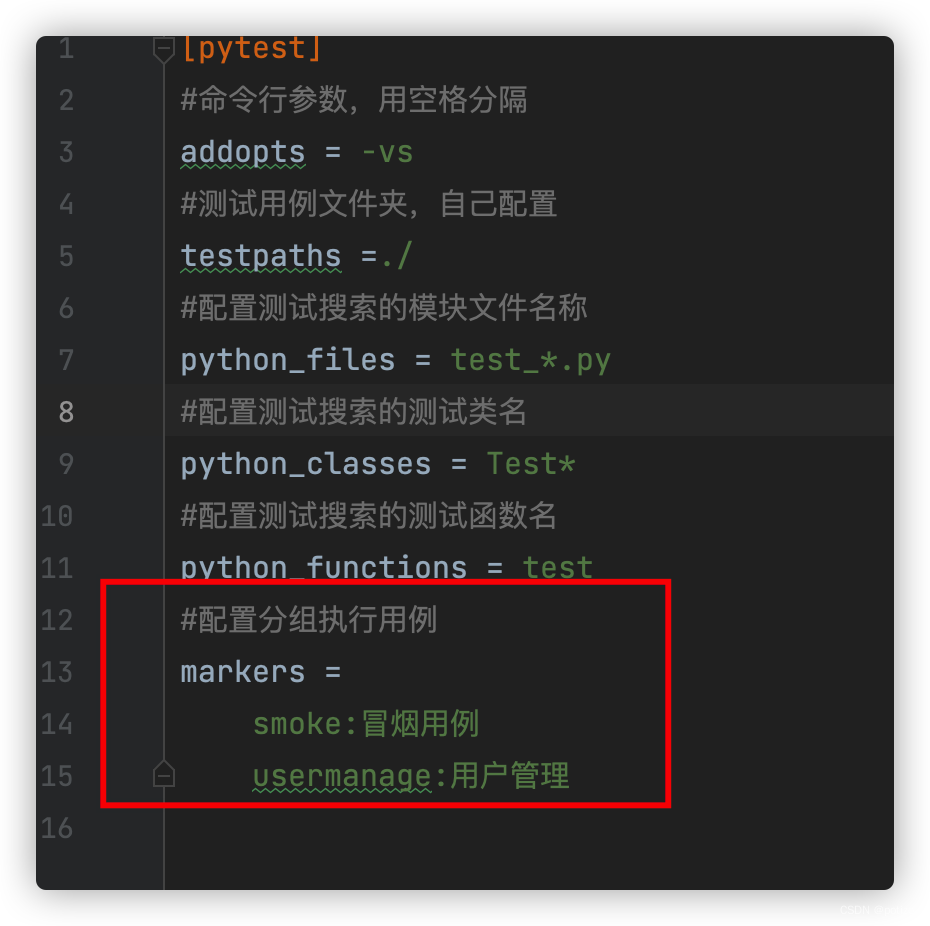
pytest初识
一、单元测试框架 (1)什么是单元测试框架? 单元测试是指在软件开发中,针对软件的最小单元(函数、方法)进行正确性的检查测试 (2)单元测试框架 java:junit和testng pytho…...
-12)
设计模式~责任链模式(Chain of Responsibility)-12
目录 (1)优点 (2)缺点 (3)使用场景 (4)注意事项: (5)应用实例: (6)经典案例 代码 责任链, …...

【ElasticSearch】(一)—— 初识ES
文章目录1. 了解ES1.1 elasticsearch的作用1.2 ELK技术栈1.3 elasticsearch和lucene1.4 为什么不是其他搜索技术?1.5 总结2. 倒排索引2.1 正向索引2.2 倒排索引2.3 正向和倒排3. ES的一些概念3.1 文档和字段3.2 索引和映射3.3 mysql与elasticsearch1. 了解ES Elasti…...
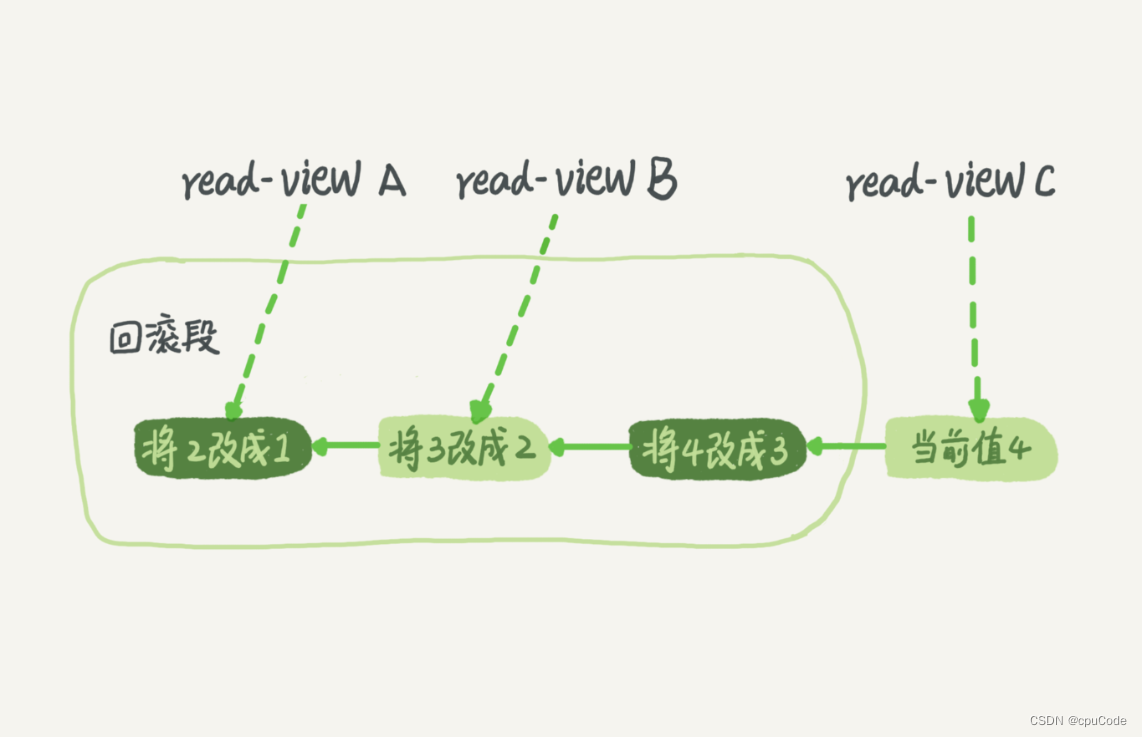
MySQL 事务隔离
MySQL 事务隔离事务隔离实现事务的启动ACID : 原子(Atomicity)、一致(Consistency)、隔离(Isolation)、永久(Durability) 多个事务可能出现问题 : 脏读 (dirty read) , 不可重复读 (non-repeatable read) , 幻读 (phantom read) 事务隔离级别 : 读未提交 (read uncommitted)…...

基础06-JS中for-in和for-of有什么区别
for…in 和 for…of 的区别 题目 for…in 和 for…of 的区别 key 和 value for…in 遍历 key , for…of 遍历 value const arr [10, 20, 30] for (let n of arr) {console.log(n) }const str abc for (let s of str) {console.log(s) }function fn() {for (let argument…...

AI视频智能分析EasyCVR视频融合平台录像计划模块搜索框细节优化
EasyCVR支持海量视频汇聚管理,可提供视频监控直播、云端录像、云存储、录像检索与回看、智能告警、平台级联、智能分析等视频服务。在录像功能上,平台可支持: 根据业务场景自定义录像计划,可支持7*24H不间断录像,支持…...
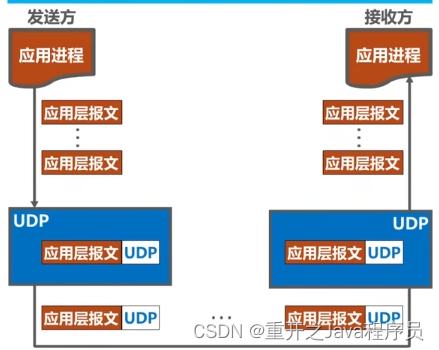
TCP和UDP对比
TCP和UDP对比 UDP(用户数据报协议) 无连接(指的是逻辑连接关系,不是物理上的连接) 支持单播、多播以及广播,也就是UDP支持一对一、一对多、一对全 面向应用报文的,对应用层交付的报文直接打包 无连接不可靠的传输服务(适用于IP电话、视频会议等实时应用),不使用流量控制和…...

CVS Health 西维斯健康EDI需求
CVS Health西维斯健康在特拉华州成立,通过旗下的 CVS Pharmacy 和 Longs Drugs 零售店以及 CVS.com 电商提供处方药、美容产品、化妆品、电影和照片加工服务、季节性商品、贺卡和方便食品。CVS Health通过使高质量的护理变得更经济、更易获得、更简单、更无缝&#…...
Anaconda配置Python科学计算库SciPy的方法
本文介绍在Anaconda环境中,安装Python语言SciPy模块的方法。 SciPy是基于Python的科学计算库,用于解决科学、工程和技术计算中的各种问题。它建立在NumPy库的基础之上,提供了大量高效、易于使用的功能,包括统计分析、信号处理、优…...
数据库基本功之复杂查询的子查询
子查询返回的值可以被外部查询使用,这样的复合查询等效与执行两个连续的查询. 1. 单行单列子查询 (>,<,,<>,>,<)内部SELECT子句只返回一行结果 2.多行单列子查询 (all, any, in,not in) all (>大于最大的,<小于最小的) SQL> select ename, sal from…...

脑机接口科普0019——大脑的分区及功能
本文禁止转载!!!! 在前文脑机接口科普0018——前额叶切除手术_sgmcy的博客-CSDN博客科普中,有个这样的一张图: 这个图呢,把大脑划分为不同的区域,然后不同的区域代表不同的功能。 …...
阿里云服务器使用教程:CentOS 7 安装JDK及Tomcat(以jdk1.8、tomcat9.0.37为例)
目录 1、下载JDK及Tomcat的安装包并上传至服务器 2、安装JDK 3、安装Tomcat 4、Tomcat启动后无法打开Tomcat首页的原因 1、下载JDK及Tomcat的安装包并上传至服务器 (1)下载JDK1.8版本压缩包 官网:Java Downloads | Oracle (…...
Ubuntu20.04下安装vm17+win10/11
一、安装vmware17 1、官网下载 vmware官网:https://www.vmware.com/cn/products/workstation-pro/workstation-pro-evaluation.html 2、安装依赖 sudo apt update sudo apt install build-essential linux-headers-generic gcc make3、权限和安装 到下载的目录下…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

spring Security对RBAC及其ABAC的支持使用
RBAC (基于角色的访问控制) RBAC (Role-Based Access Control) 是 Spring Security 中最常用的权限模型,它将权限分配给角色,再将角色分配给用户。 RBAC 核心实现 1. 数据库设计 users roles permissions ------- ------…...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...
数据挖掘是什么?数据挖掘技术有哪些?
目录 一、数据挖掘是什么 二、常见的数据挖掘技术 1. 关联规则挖掘 2. 分类算法 3. 聚类分析 4. 回归分析 三、数据挖掘的应用领域 1. 商业领域 2. 医疗领域 3. 金融领域 4. 其他领域 四、数据挖掘面临的挑战和未来趋势 1. 面临的挑战 2. 未来趋势 五、总结 数据…...

react-pdf(pdfjs-dist)如何兼容老浏览器(chrome 49)
之前都是使用react-pdf来渲染pdf文件,这次有个需求是要兼容xp环境,xp上chrome最高支持到49,虽然说iframe或者embed都可以实现预览pdf,但为了后续的定制化需求,还是需要使用js库来渲染。 chrome 49测试环境 能用的测试…...

Centos 7 服务器部署多网站
一、准备工作 安装 Apache bash sudo yum install httpd -y sudo systemctl start httpd sudo systemctl enable httpd创建网站目录 假设部署 2 个网站,目录结构如下: bash sudo mkdir -p /var/www/site1/html sudo mkdir -p /var/www/site2/html添加测试…...

