吴恩达深度学习笔记:超 参 数 调 试 、 Batch 正 则 化 和 程 序 框 架(Hyperparameter tuning)3.8-3.9
目录
- 第二门课: 改善深层神经网络:超参数调试、正 则 化 以 及 优 化 (Improving Deep Neural Networks:Hyperparameter tuning, Regularization and Optimization)
- 第三周: 超 参 数 调 试 、 Batch 正 则 化 和 程 序 框 架(Hyperparameter tuning)
- 3.8 Softmax 回归(Softmax regression)
第二门课: 改善深层神经网络:超参数调试、正 则 化 以 及 优 化 (Improving Deep Neural Networks:Hyperparameter tuning, Regularization and Optimization)
第三周: 超 参 数 调 试 、 Batch 正 则 化 和 程 序 框 架(Hyperparameter tuning)
3.8 Softmax 回归(Softmax regression)
到目前为止,我们讲到过的分类的例子都使用了二分分类,这种分类只有两种可能的标记 0 或 1,这是一只猫或者不是一只猫,如果我们有多种可能的类型的话呢?有一种 logistic回归的一般形式,叫做 Softmax 回归,能让你在试图识别某一分类时做出预测,或者说是多种分类中的一个,不只是识别两个分类,我们来一起看一下。

假设你不单需要识别猫,而是想识别猫,狗和小鸡,我把猫加做类 1,狗为类 2,小鸡是类 3,如果不属于以上任何一类,就分到“其它”或者说“以上均不符合”这一类,我把它叫做类 0。这里显示的图片及其对应的分类就是一个例子,这幅图片上是一只小鸡,所以是类3,猫是类 1,狗是类 2,我猜这是一只考拉,所以以上均不符合,那就是类 0,下一个类 3,以此类推。我们将会用符号表示,我会用大写的C来表示你的输入会被分入的类别总个数,在这个例子中,我们有 4 种可能的类别,包括“其它”或“以上均不符合”这一类。当有 4 个分类时,就是 0、1、2、3。
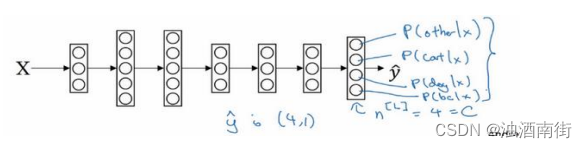
在这个例子中,我们将建立一个神经网络,其输出层有 4 个,或者说C个输出单元,因此n,即输出层也就是L层的单元数量,等于 4,或者一般而言等于C。我们想要输出层单元的数字告诉我们这 4 种类型中每个的概率有多大,所以这里的第一个节点(最后输出的第 1个方格+圆圈)输出的应该是或者说我们希望它输出“其它”类的概率。在输入X的情况下,这个(最后输出的第 2 个方格+圆圈)会输出猫的概率。在输入X的情况下,这个会输出狗的概率(最后输出的第 3 个方格+圆圈)。在输入X的情况下,输出小鸡的概率(最后输出的第 4 个方格+圆圈),我把小鸡缩写为 bc(baby chick)。因此这里的 y ^ \hat{y} y^将是一个4 × 1维向量,因为它必须输出四个数字,给你这四种概率,因为它们加起来应该等于 1,输出中的四个数字加起来应该等于 1。
让你的网络做到这一点的标准模型要用到 Softmax 层,以及输出层来生成输出,让我把式子写下来,然后回过头来,就会对 Softmax 的作用有一点感觉了。
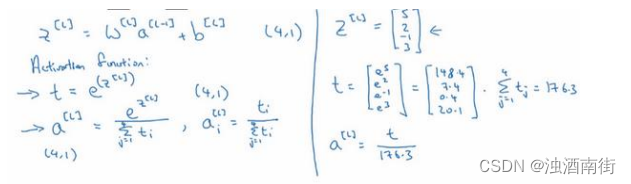
在神经网络的最后一层,你将会像往常一样计算各层的线性部分, z [ l ] z^{[l]} z[l]这是最后一层的z变量,记住这是大写L层,和往常一样,计算方法是 z [ l ] = W [ l ] a [ L − 1 ] + b [ l ] z^{[l]} = W^{[l]}a^{[L−1]} + b^{[l]} z[l]=W[l]a[L−1]+b[l],算出了𝑧之后,你需要应用 Softmax 激活函数,这个激活函数对于 Softmax 层而言有些不同,它的作用是这样的。首先,我们要计算一个临时变量,我们把它叫做 t,它等于 e z [ l ] e ^{z^{[l]}} ez[l],这适用于每个元素,而这里的 z [ l ] z^{[l]} z[l],在我们的例子中, z [ l ] z^{[l]} z[l]是 4×1 的,四维向量 t = e z [ l ] t= e^{z^{[l]}} t=ez[l],这是对所有元素求幂,t也是一个 4×1 维向量,然后输出的 a [ l ] a^{[l]} a[l],基本上就是向量𝑡,但是会归一化,使和为 1。因此 a [ l ] = e z [ l ] ∑ i = 1 4 t i a^{[l]} =\frac{e^{z^{[l]}}}{\sum_{i=1}^4{t_i}} a[l]=∑i=14tiez[l],换句话说, a [ l ] a^{[l]} a[l]也是一个 4×1 维向量,而这个四维向量的第i个元素,我把它写下来, a i [ l ] = t i ∑ i = 1 4 t i a_i^{[l]} =\frac{t_i}{\sum_{i=1}^4{t_i}} ai[l]=∑i=14titi,以防这里的计算不够清晰易懂,我们马上会举个例子来详细解释。
我们来看一个例子,详细解释,假设你算出了 z [ l ] , z [ l ] z^{[l]},z^{[l]} z[l],z[l]是一个四维向量,假设为 z [ l ] = [ 5 2 − 1 3 ] z^{[l]} =\begin{bmatrix} 5\\2\\-1\\3 \end{bmatrix} z[l]= 52−13 ,我们要做的就是用这个元素取幂方法来计算𝑡,所以 t = [ e 5 e 2 e − 1 e 3 ] t =\begin{bmatrix} e^5\\e^2\\e^{-1}\\e^3 \end{bmatrix} t= e5e2e−1e3 ,如果你按一下计算器就会得到以下值 t = [ 148.4 7.4 0.4 20.1 ] t =\begin{bmatrix} 148.4\\7.4\\0.4\\20.1 \end{bmatrix} t= 148.47.40.420.1 ,我们从向量𝑡得到向量 a [ l ] a^{[l]} a[l]就只需要将这些项目归一化,使总和为 1。如果你把𝑡的元素都加起来,把这四个数字加起来,得到 176.3,最终 a [ l ] = t 176.3 a^{[l]}=\frac{t}{176.3} a[l]=176.3t。
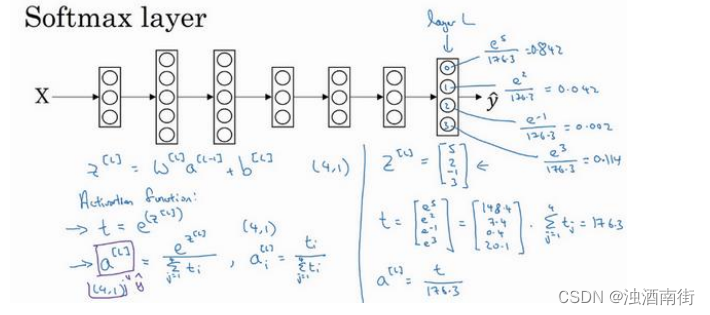
例如这里的第一个节点,它会输出 e 5 176.3 \frac{e^5}{176.3} 176.3e5= 0.842,这样说来,对于这张图片,如果这是你得到的𝑧值( [ 5 2 − 1 3 ] \begin{bmatrix} 5\\2\\-1\\3 \end{bmatrix} 52−13 ),它是类 0 的概率就是 84.2%。下一个节点输出 e 2 176.3 \frac{e^2}{176.3} 176.3e2= 0.042,也就是 4.2%的几率。下一个是 e − 1 176.3 \frac{e^{-1}}{176.3} 176.3e−1= 0.002。最后一个是 e 3 176.3 \frac{e^{3}}{176.3} 176.3e3= 0.114,也就是 11.4%的概率属于类 3,也就是小鸡组,对吧?这就是它属于类 0,类 1,类 2,类 3 的可能性。
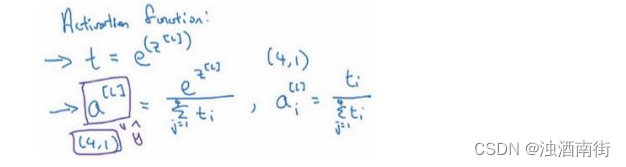
神经网络的输出 a [ l ] a^{[l]} a[l],也就是 y ^ \hat{y} y^,是一个 4×1 维向量,这个 4×1 向量的元素就是我们算出来的这四个数字( [ 0.842 0.042 0.002 0.114 ] \begin{bmatrix} 0.842\\0.042\\0.002\\0.114 \end{bmatrix} 0.8420.0420.0020.114 ),所以这种算法通过向量 z [ l ] z^{[l]} z[l]计算出总和为 1 的四个概率。
如果我们总结一下从 z [ l ] z^{[l]} z[l]到 a [ l ] a^{[l]} a[l]的计算步骤,整个计算过程,从计算幂到得出临时变量𝑡,再归一化,我们可以将此概括为一个 Softmax 激活函数。设 a [ l ] = g [ l ] a^{[l]} = g^{[l]} a[l]=g[l]( z [ l ] z^{[l]} z[l]),这一激活函数的与众不同之处在于,这个激活函数𝑔 需要输入一个 4×1 维向量,然后输出一个 4×1 维向量。之前,我们的激活函数都是接受单行数值输入,例如 Sigmoid 和 ReLu 激活函数,输入一个实数,输出一个实数。Softmax 激活函数的特殊之处在于,因为需要将所有可能的输出归一化,就需要输入一个向量,最后输出一个向量。
那么 Softmax 分类器还可以代表其它的什么东西么?我来举几个例子,你有两个输入 x 1 x_1 x1, x 2 x_2 x2,它们直接输入到 Softmax 层,它有三四个或者更多的输出节点,输出 y ^ \hat{y} y^,我将向你展示一个没有隐藏层的神经网络,它所做的就是计算 z [ 1 ] = W [ 1 ] x + b [ 1 ] z^{[1]} = W^{[1]}x + b^{[1]} z[1]=W[1]x+b[1],而输出的出 a [ l ] a^{[l]} a[l],或者说 y ^ \hat{y} y^, a [ l ] = y = g ( z [ l ] ) a^{[l]} = y = g(z[l]) a[l]=y=g(z[l]),就是 z [ 1 ] z^{[1]} z[1]的 Softmax 激活函数,这个没有隐藏层的神经网络应该能让你对 Softmax 函数能够代表的东西有所了解。
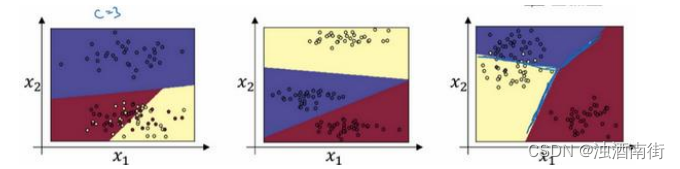
这个例子中(左边图),原始输入只有 x 1 x_1 x1和 x 2 x_2 x2,一个𝐶 = 3个输出分类的 Softmax 层能够代表这种类型的决策边界,请注意这是几条线性决策边界,但这使得它能够将数据分到 3个类别中,在这张图表中,我们所做的是选择这张图中显示的训练集,用数据的 3 种输出标签来训练 Softmax 分类器,图中的颜色显示了 Softmax 分类器的输出的阈值,输入的着色是基于三种输出中概率最高的那种。因此我们可以看到这是 logistic 回归的一般形式,有类似线性的决策边界,但有超过两个分类,分类不只有 0 和 1,而是可以是 0,1 或 2。
这是(中间图)另一个 Softmax 分类器可以代表的决策边界的例子,用有三个分类的数据集来训练,这里(右边图)还有一个。对吧,但是直觉告诉我们,任何两个分类之间的决策边界都是线性的,这就是为什么你看到,比如这里黄色和红色分类之间的决策边界是线性边界,紫色和红色之间的也是线性边界,紫色和黄色之间的也是线性决策边界,但它能用这些不同的线性函数来把空间分成三类。
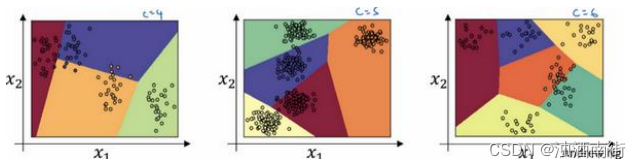
我们来看一下更多分类的例子,这个例子中(左边图)𝐶 = 4,因此这个绿色分类和Softmax 仍旧可以代表多种分类之间的这些类型的线性决策边界。另一个例子(中间图)是𝐶 = 5类,最后一个例子(右边图)是𝐶 = 6,这显示了 Softmax 分类器在没有隐藏层的情况下能够做到的事情,当然更深的神经网络会有𝑥,然后是一些隐藏单元,以及更多隐藏单元等等,你就可以学习更复杂的非线性决策边界,来区分多种不同分类。
我希望你了解了神经网络中的 Softmax 层或者 Softmax 激活函数有什么作用,下一个视频中,我们来看一下你该怎样训练一个使用 Softmax 层的神经网络。
相关文章:

吴恩达深度学习笔记:超 参 数 调 试 、 Batch 正 则 化 和 程 序 框 架(Hyperparameter tuning)3.8-3.9
目录 第二门课: 改善深层神经网络:超参数调试、正 则 化 以 及 优 化 (Improving Deep Neural Networks:Hyperparameter tuning, Regularization and Optimization)第三周: 超 参 数 调 试 、 Batch 正 则 化 和 程 序 框 架(Hyperparameter …...

SQL 语言:数据控制
文章目录 概述授权(GRANT)销权(REVOKE)总结 概述 SQL语言中的数据控制权限分配是数据库管理的重要组成部分,它涉及到如何合理地为用户分配对数据库资源的访问和使用权限。 权限类型:在SQL中,权限主要分为…...

『ZJUBCA Weekly Feed 07』MEV | AO超并行计算机 | Eigen layer AVS生态
一文读懂MEV:区块链的黑暗森林法则 01 💡TL;DR 这篇文章介绍了区块链中的最大可提取价值(MEV)概念,MEV 让矿工和验证者通过抢先交易、尾随交易和三明治攻击等手段获利,但也导致网络拥堵和交易费用增加。为了…...

正点原子延时函数delay_ms延时失效的原因
1、问题陈述 今天在测试小车程序的时候使用了如下代码,发现延时并没有达到期望的4s,而是仅仅延时了0.4s左右,本来以为少加了个0,最后在我多次测试下来,发现在延时大约超过2s的时候就会失效。 while(1){Set_Pwm(6000,60…...

MySQL 满足条件函数中使用查询最大值函数
在实际的数据库操作中,我们常常需要根据某些条件找到最大值并据此进行下一步的操作。例如,在一个包含订单信息的表中,可能需要找到特定客户的最大订单金额,并据此进行某些统计或决策。MySQL 提供了多种函数和查询方法,…...
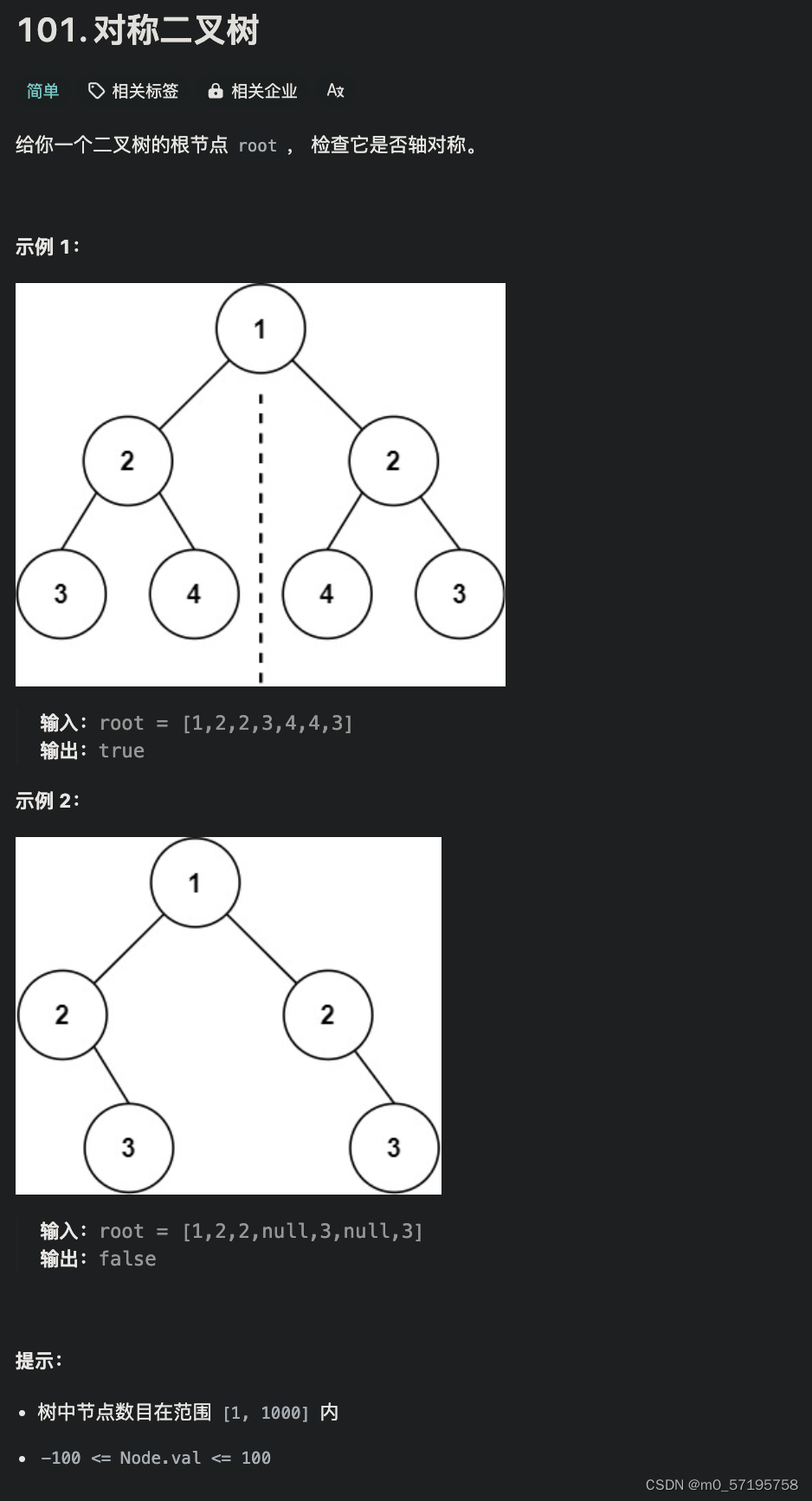
Java | Leetcode Java题解之第101题对称二叉树
题目: 题解: class Solution {public boolean isSymmetric(TreeNode root) {return check(root, root);}public boolean check(TreeNode u, TreeNode v) {Queue<TreeNode> q new LinkedList<TreeNode>();q.offer(u);q.offer(v);while (!q.…...

【区块链】智能合约漏洞测试
打开Ganache vscode打开智能合约漏洞工程 合约内容 pragma solidity >0.8.3;contract EtherStore {mapping(address > uint) public balances;function deposit() public payable {balances[msg.sender] msg.value;emit Balance(balances[msg.sender]);}function with…...
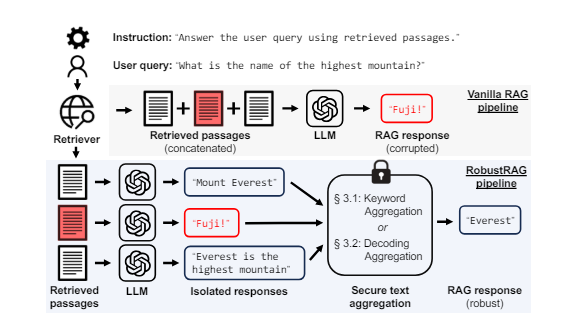
大模型主流 RAG 框架TOP10
节前,我们组织了一场算法岗技术&面试讨论会,邀请了一些互联网大厂朋友、今年参加社招和校招面试的同学。 针对大模型技术趋势、大模型落地项目经验分享、新手如何入门算法岗、该如何准备面试攻略、面试常考点等热门话题进行了深入的讨论。 总结链接…...
第八次javaweb作业
我们小组课程设计的题目是:超市管理系统,我认领的模块是:商品信息管理 controller package com.example.supermarker.controller;import com.example.supermarker.pojo.MerchInfo; import com.example.supermarker.pojo.PageBean; import c…...
)
js积累四 (读json文件)
function ReadRadioJson() {var url "../radio.json" //json文件url,本地的就写本地的位置,如果是服务器的就写服务器的路径var request new XMLHttpRequest();request.open("get", url, false); //设置请求方法与路径request.sen…...

关于我转生从零开始学C++这件事:升级Lv.25
❀❀❀ 文章由不准备秃的大伟原创 ❀❀❀ ♪♪♪ 若有转载,请联系博主哦~ ♪♪♪ ❤❤❤ 致力学好编程的宝藏博主,代码兴国!❤❤❤ OK了老铁们,又是一个周末,大伟又来继续给大家更新我们的C的内容了。那么根据上一篇博…...

mysql中text,longtext,mediumtext区别
文章目录 一.概览二、字节限制不同三、I/O 不同四、行迁移不同 一.概览 在 MySQL 中,text、mediumtext 和 longtext 都是用来存储大量文本数据的数据类型。 TEXT:TEXT 数据类型可以用来存储最大长度为 65,535(2^16-1)个字符的文本数据。如果存储的数据…...
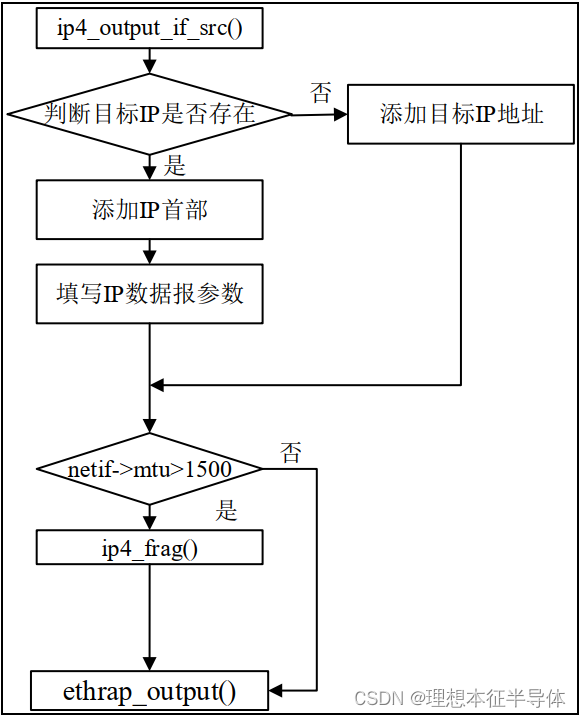
IP协议说明
文章目录 前言一、IP协议的简介二、IP数据报1.IP 数据报结构2.IP 数据报的分片解析3.IP 数据报的分片重装 三、IP 数据报的输出四、IP 数据报的输入 前言 IP 指网际互连协议, Internet Protocol 的缩写,是 TCP/IP 体系中的网络层协议。设计 IP 的目的是…...
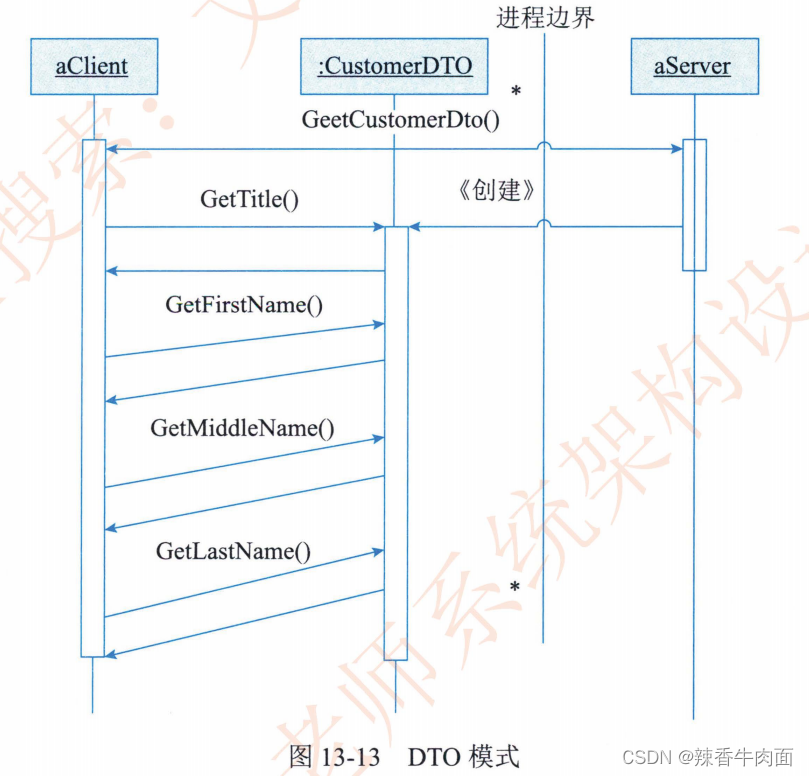
第13章 层次式架构设计理论与实践
层次式架构的核心思想是将系统组成为一种层次结构,每一层为上层服务,并作为下层客户。其实不管是分层还是其他的架构都是为了解耦,更好的复用,只要秉承着这种思想去理解一切都迎刃而解了。 13.1 层次上体系结构概述 回顾一下软件…...

FreeRtos进阶——消息队列的操作逻辑
消息队列(queue) 在不同的任务之间,如果我们需要互相之间通信,使用全局变量进行通信,是一种不安全的通信的方式。为保证线程安全,我们需要引入消息队列的通信方式。 粗暴的消息队列 为保证线程的安全&am…...

WordPress搭建流程
1. 简介 WordPress 是一个 PHP 编写的网站制作平台。WordPress 本身免费,并且拥有众多的主题可以使用,适合用于搭建个人博客、公司官网、独立站等。 2. 环境准备 2.1 WordPress 下载 WordPress 可以在 Worpress中文官网 下载(如果后续要将后台调成中文的话,一定要从中文…...

数据集004:跌倒检测数据集 (含数据集下载链接)
数据集简介: 该数据集为跌倒检测数据集,属于imageclassify任务,分为fall和nofall两大类,累计共1000张图片,均为人工标注 xml格式,可用于yolo训练。 数据集链接:跌倒检测数据集(1000…...

苹果与OpenAI合作在即:iOS 18中的ChatGPT引发期待与担忧
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...

Android 逆向学习【2】——APK基本结构
APK安装在安卓机器上的,相当于就是windows的exe文件 APK实际上是个压缩包 只要是压缩的东西 .jar也是压缩包 里面是.class(java编译后的一些东西) APK是Android Package的缩写,即Android安装包。而apk文件其实就是一个压缩包,我们可以将apk文件的后…...

你对仲裁裁决不服怎么办?我教你四个狠招!
你对仲裁裁决不服怎么办?我教你四个狠招! 这个标题是什么意思呢?也就是说,当你(或用人单位)向劳动仲裁委提出仲裁申请后,但劳动仲裁结果没有维护你的权益,或者你不满意,…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...
