第十四届蓝桥杯c++研究生组
A 混乘数字

关键思路是求每个十进制数的数字以及怎么在一个数组中让判断所有的数字次数相等。
求每个十进制的数字
while(n!=0){int x = n%10;//x获取了n的每一个位数字n/=10;}
扩展:求二进制的每位数字 (注意:进制转换、1的个数、位运算)
x >> k & 1//k代表第几个位置
判断几个数中的数字次数相等
下面是判断3个数中的数字次数相等
bool swap(int n,int i,int j){int a[]={0,0,0,0,0,0,0,0,0,0};while(n!=0){int x = n%10;a[x]++;n/=10;}while(i!=0){int x = i%10;a[x]--;i/=10;}while(j!=0){int x = j%10;a[x]--;j/=10;}for(int i=0;i<=9;i++){if(a[i]!=0){return false;}}return true;
}
完整代码:
#include <iostream>
#include <cmath>
using namespace std;bool swap(int n,int i,int j){int a[]={0,0,0,0,0,0,0,0,0,0};while(n!=0){int x = n%10;a[x]++;n/=10;}while(i!=0){int x = i%10;a[x]--;i/=10;}while(j!=0){int x = j%10;a[x]--;j/=10;}for(int i=0;i<=9;i++){if(a[i]!=0){return false;}}return true;
}bool is(int n){for(int i=2;i<=sqrt(n)+1;i++){if(n%i==0){int j = n/i;if(swap(n,i,j)){return true;}} }return false;
} int main(){int sum=0;for(int i=1;i<=1000000;i++){if(is(i)){sum++;}}cout << sum << endl;return 0;
}
B 钉板上的正方形

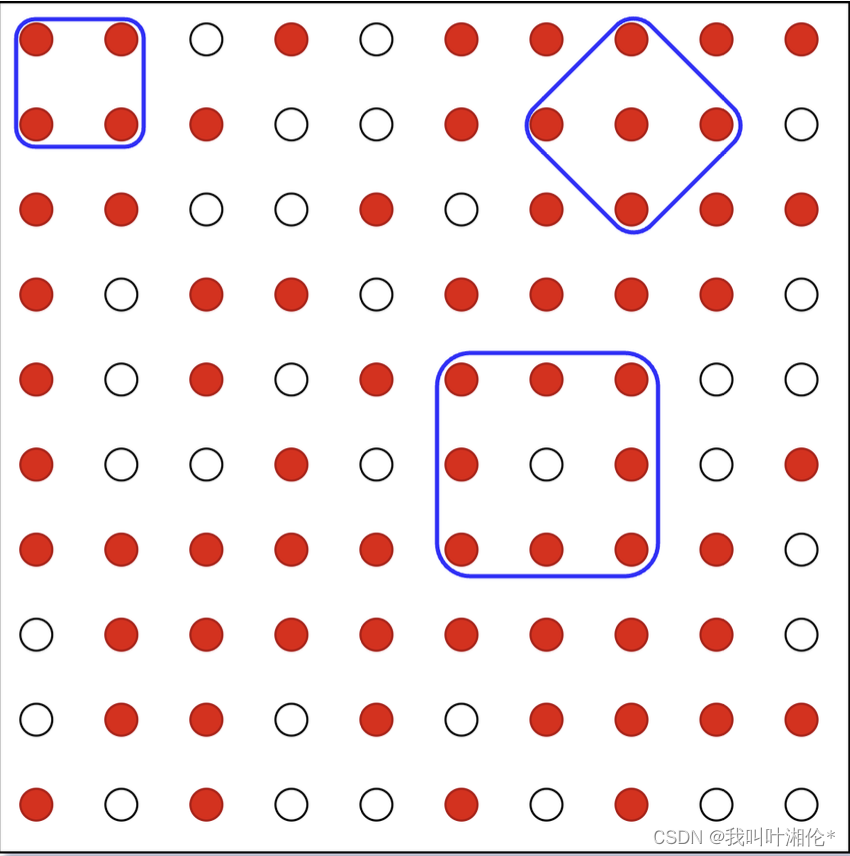

爆搜
#include <bits/stdc++.h>
using namespace std;int a[][20]={{1,1,0,1,0,1,1,1,1,1},{1,1,1,0,0,1,1,1,1,0},{1,1,0,0,1,0,1,1,1,1},{1,0,1,1,0,1,1,1,1,0},{1,0,1,0,1,1,1,1,0,0},{1,0,0,1,0,1,0,1,0,1},{1,1,1,1,1,1,1,1,1,0},{0,1,1,1,1,1,1,1,1,0},{0,1,1,0,1,0,1,1,1,1},{1,0,1,0,0,1,0,1,0,0},
};
map<int, int> mp;
int ans;int main(){for(int i=0;i<10;i++){for(int j=0;j<10;j++){if(a[i][j]==0){continue;}for(int k=i+1;k<10;k++){for(int p=0;p<=j;p++){if(a[k][p]==0){continue;}if (a[k + j - p][p + k - i] == 1 && a[i + j - p][j + k - i] == 1){int len = (j - p) * (j - p) + (k - i) * (k - i);if (mp[len] == 0) {ans++; mp[len] = 1;}}}}}}cout << ans; return 0;
}
扩展map的用法
map容器是一个键值对key—value的映射,其内部实现是一颗以key为关键吗的红黑树。map的key和value可以是任意类型,其中key必须定义小于号运算符。
map的声明
map<key_type,value_type> name;
//列子
map<int int> mp;
map<string,int> mp;
方法
size/empty/clear/begin/end/insert/erase/find/[]
C 整数变换
求每个数的位的数字。详细见A题。注意数据范围
#include <iostream>
#include <algorithm>using namespace std;long long n,sum;int main(){cin >> n;while(n>0){long long x=n;while(x!=0){int aa=x%10;n-=aa;x/=10;}sum++; }cout << sum <<endl;return 0;
}
D 躲炮弹

**最初思路:**遍历从L到R,但是如果随机遍历每个L到R中的每个数,最后得到的最小移动数是不一样。即行不通。
解题思路:
分三种情况:
- 当n<l时。不用移动,输出0.
- 当n>=l&&n<=r时。即考虑移动l-1的步数和移动到r右边的符合条件之间的最小数。
- 当n>r时。即往左右移动找符合最小移动的步数。
完整代码
#include <bits/stdc++.h>using namespace std;long long n,l,r;
long long ans;bool check(int x){for(int i=1;i<=sqrt(x);i++){if(x%i==0){int t = x/i;if(i>=l && i<=r){return true;}if(t>=l && t<=r){return true;}}}return false;
}int main(){cin >> n >> l >> r;if(n<l){cout << 0 << endl;return 0;}if(n>=l&&n<=r){ans = n-(l-1);for(int i=1;i<=2000;i++){if(!check(r+i)){ans = min(r+i-n,ans);break;}}cout << ans <<endl;return 0;}for(int i=1;i<=2000;i++){if(!check(n+i) || !check(n-i)){cout << i << endl;return 0;}}return 0;
}
E 最大区间
单调栈对两个方向上各使用使用一次单调栈求得距离i位置最近的比它小的数。
完整代码:
#include <bits/stdc++.h>using namespace std;const int N = 3e5+5;long long a[N],l[N];int main(){long long n,ans=0;cin >> n;for(int i=0;i<n;i++){cin >> a[i];}stack<pair<int,int>> s;stack<pair<int,int>> ss;s.push({-1,-1});ss.push({-1,-1});for(int i=0;i<n;i++){while(s.size()&&a[i]<=s.top().first)s.pop();l[i]=a[i]*(i-s.top().second);s.push({a[i],i});}for(int i=n-1;i>=0;i--){while(ss.size()&&a[i]<=ss.top().first)ss.pop();ans=max(ans,(long long)l[i]+a[i]*(ss.top().second-i-1));ss.push({a[i],i});}cout<<ans;return 0;
}
扩展 栈的使用先进后出
声明
stack<int> s;
stack<pair<int,int>> ss;
s.push();
s.pop();
选段排序

思路:主要利用大顶堆和小顶堆进行扩展区间。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
#define int long long
#define endl '\n'
#define INF 0x3f3f3f3f3f3f3f3f
const int N=2e5+10;
priority_queue<int,vector<int>,less<int>> q1;//大顶堆
priority_queue<int,vector<int>,greater<int>> q2;//小顶堆
int a[N];
signed main()
{std::ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int n,p,q;cin>>n>>p>>q;for(int i=1;i<=n;i++)cin>>a[i];sort(a+p,a+q+1);int minn=a[p],maxx=a[q];int sub=maxx-minn;for(int i=p;i<=q;i++){q1.push(a[i]);q2.push(a[i]);}for(int i=q+1;i<=n;i++)//[p,q]拓展右边界[L,q]{int t=q1.top();if(a[i]<minn) minn=a[i];if(a[i]<t){q1.pop();q1.push(a[i]);sub=max(sub,q1.top()-minn);} }for(int i=p-1;i>=1;i--)//[p,q]拓展左边界[p,R]{int t=q2.top();if(a[i]>maxx) maxx=a[i];if(a[i]>t){q2.pop();q2.push(a[i]);sub=max(sub,maxx-q2.top());} }cout<<sub;return 0;
}
相关文章:

第十四届蓝桥杯c++研究生组
A 混乘数字 关键思路是求每个十进制数的数字以及怎么在一个数组中让判断所有的数字次数相等。 求每个十进制的数字 while(n!0){int x n%10;//x获取了n的每一个位数字n/10;}扩展:求二进制的每位数字 (注意:进制转换、1的个数、位运算&#…...

KDD 2024|基于隐空间因果推断的微服务系统根因定位
简介:本文介绍了由清华大学、南开大学、eBay、微软、中国科学院计算机网络信息中心等单位共同合作的论文《基于隐空间因果推断的受限可观测性场景的微服务系统根因定位》。该论文已被KDD 2024会议录用。 论文标题:Microservice Root Cause Analysis Wit…...
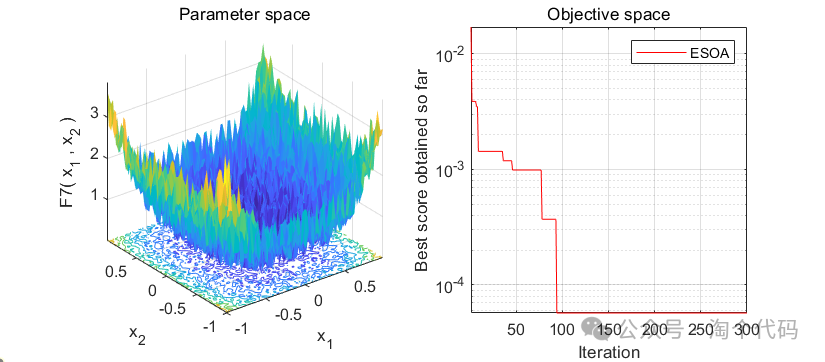
白鹭群优化算法,原理详解,MATLAB代码免费获取
白鹭群优化算法(Egret Swarm Optimization Algorithm,ESOA)是一种受自然启发的群智能优化算法。该算法从白鹭和白鹭的捕食行为出发,由三个主要部分组成:坐等策略、主动策略和判别条件。将ESOA算法与粒子群算法(PSO)、遗传算法(GA)…...
【源码】2024完美运营版商城/拼团/团购/秒杀/积分/砍价/实物商品/虚拟商品等全功能商城
后台可以自由拖曳修改前端UI页面 还支持虚拟商品自动发货等功能 前端UNIAPP 后端PHP 一键部署版本 获取方式: 微:uucodes...
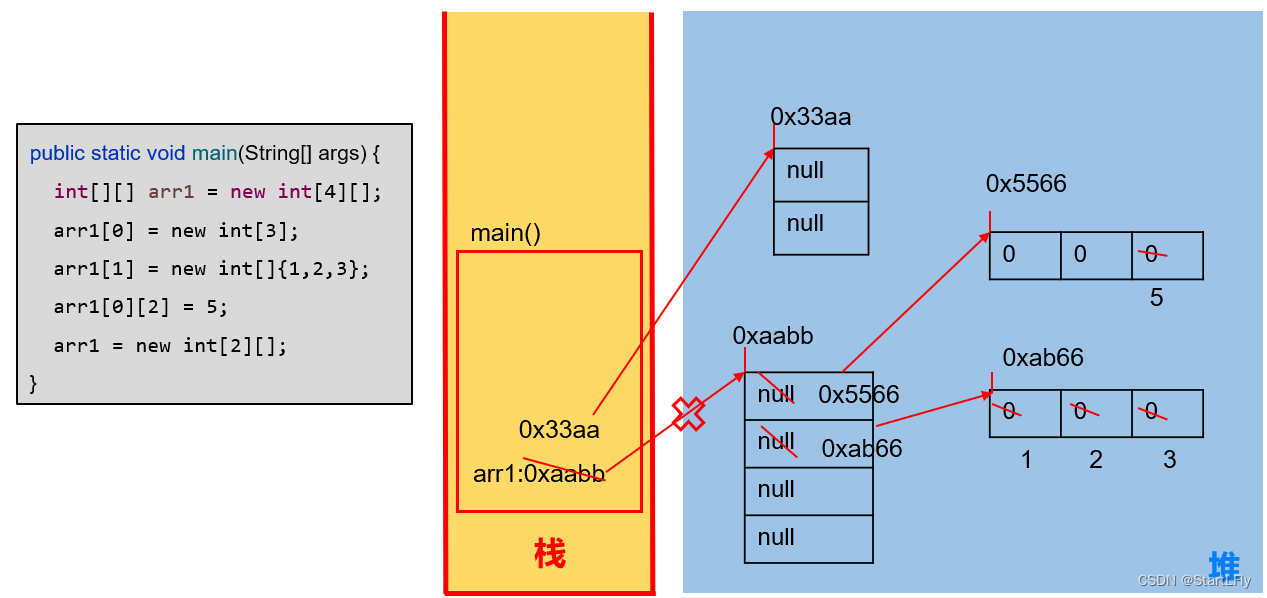
Java-数组内存解析
文章目录 1.内存的主要结构:栈、堆2.一维数组的内存解析3.二维数组的内存解析 1.内存的主要结构:栈、堆 2.一维数组的内存解析 举例1:基本使用 举例2:两个变量指向一个数组 3.二维数组的内存解析 举例1: 举例2&am…...

Spring Cache --学习笔记
一、概述 Spring Cache 是一个框架,实现了基于注解的缓存功能,只需要简单地加一个注解,就能实现缓存功能。 Spring Cache 提供了一层抽象,底层可以切换不同的缓存实现,例如: EHCache Caffeine Redis(常…...

NTP服务的DDoS攻击:原理和防御
NTP协议作为一种关键的互联网基础设施组件,旨在确保全球网络设备间的时钟同步,对于维护数据一致性和安全性至关重要。然而,其设计上的某些特性也为恶意行为者提供了发动大规模分布式拒绝服务(DDoS)攻击的机会。以下是NTP服务DDoS攻击及其防御…...

【面试干货】事务的并发问题(脏读、不可重复读、幻读)与解决策略
【面试干货】事务的并发问题(脏读、不可重复读、幻读)与解决策略 一、脏读(Dirty Read)二、不可重复读(Non-repeatable Read)三、幻读(Phantom Read)四、总结 💖The Begi…...

函数式接口:现代编程的利器
1. 引言 在软件开发的演进过程中,函数式编程(Functional Programming, FP)逐渐显露头角,成为解决复杂问题的有效工具之一。函数式接口作为函数式编程的核心概念之一,其重要性不言而喻。本文将深入探讨函数式接口的概念…...

2022职称继续教育--深入实施新时代人才强国战略 加快建设世界重要人才中心和创新高地
单选题(共7题,每题5分) 1、()实行职位职级制工资为主。 D、中长线科研重要岗位人员 2、建设世界重要人才中心和创新高地有()个阶段目标。 B、三 3、综合国力竞争说到底是(…...

kube-prometheus-stack 识别 k8s 集群内所有的 ServiceMonitor 和 PrometheusRule
默认情况下,kube-prometheus-stack 只自己创建的 ServiceMonitor,如果 k8s 集群内有多个非 kube-prometheus-stack 创建的 ServiceMonitor,不会被识别到。PrometheusRule 同理。 要识别所有的 ServiceMonitor 和 PrometheusRule ,…...

Android 图片加载glide库 一次通关
前言 Glide是一个由Bumptech开发的开源图片加载库,专门用于Android平台。它被广泛应用于Android应用中,以简化图片加载过程,并提高性能和效率。 Glide能够快速加载图片,同时减少页面加载时间和内存消耗。Glide具有强大的缓存机制…...

Spring OAuth2:开发者的安全盾牌!(上)
何利用Spring OAuth2构建坚不可摧的安全体系?如何使用 OAuth2 从跨域挑战到性能优化,每一个环节都为你的应用保驾护航? 文章目录 Spring OAuth2 详解1. 引言简述OAuth2协议的重要性Spring Framework对OAuth2的支持概述 2. 背景介绍2.1 OAuth2…...

设计模式使用(成本扣除)
前言 名词解释 基础名词 订单金额:用户下单时支付的金额,这个最好理解 产品分成:也就是跟其他人合做以后我方能分到的金额,举个例子,比如用户订单金额是 100 块,我方的分成是 80%,那么也就是…...
——C++的标准输出流)
输入输出(2)——C++的标准输出流
目录 一、C的标准输出流 (一)cout、cerr和clog流对象 1、cout 流对象 2、cerr 流对象 3、clog流对象 (二)用函数put输出字符 (三)用函数 write 输出字符 一、C的标准输出流 标准输出流——流向标准输…...

C语言序列化和反序列化--TPL(一)
TPL TPL说明网站 C语言中高效的序列化 您可以使用tpl快速轻松地存储和重新加载C数据。Tpl是一个用于序列化C数据的库。数据以自然二进制形式存储。该API很小,并试图保持“不碍事”。Tpl可以序列化许多C数据类型,包括结构。Tpl与文件、内存缓冲区和文件…...

Session + JWT + Cookie
00:HTTP无状态(为了保持状态,前端好麻烦,又要自己存,又要想办法带出去,于是使用cookie) 01:Cookie 将用户信息,在每次请求时候 带给后端(但是自己存储大小有…...
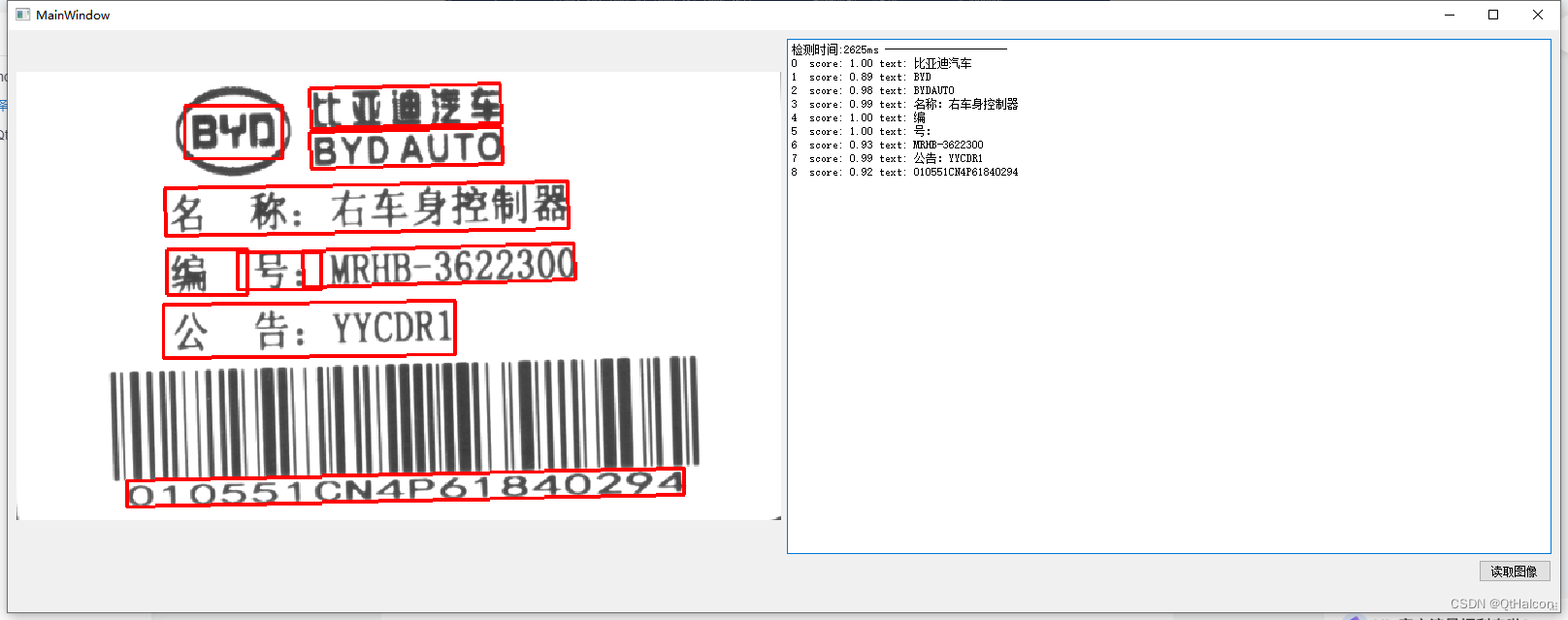
PaddleOCR2.7+Qt5
章节一:Windows 下的 PIP 安装 官网安装教程地址 按照里面的教程去安装 如果使用cuda版本的还要安装tensorrt,不然后面运行demo程序的程序会报如下错。 下载TensorRT 8版本,tensorrt下载地址 章节二:编译源码 进入官网源码地址 下…...

在Android中解析XML文件并在RecyclerView中显示
1. 引言 最近工作有解析外部xml文件在App中显示的需求,特来写篇文章记录一下,方便下次使用。 2. 准备工作 首先,在项目的AndroidManifest.xml文件中添加读取外部存储的权限声明。 <uses-permission android:name"android.permiss…...

Notes for video: EDC-Con 2022/01 - EDC Conceptual Overview and Architecture
Eclipse Dataspace Connector 中文概念 Eclipse Dataspace Connector (EDC) 是一个开源项目,旨在提供一种标准化的方法来连接和共享数据空间中的数据。它是 Eclipse Foundation 下的一个项目,目标是促进数据共享和数据交换的互操作性。以下是 EDC 的一些…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

AxureRP-Pro-Beta-Setup_114413.exe (6.0.0.2887)
Name:3ddown Serial:FiCGEezgdGoYILo8U/2MFyCWj0jZoJc/sziRRj2/ENvtEq7w1RH97k5MWctqVHA 注册用户名:Axure 序列号:8t3Yk/zu4cX601/seX6wBZgYRVj/lkC2PICCdO4sFKCCLx8mcCnccoylVb40lP...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...

AD学习(3)
1 PCB封装元素组成及简单的PCB封装创建 封装的组成部分: (1)PCB焊盘:表层的铜 ,top层的铜 (2)管脚序号:用来关联原理图中的管脚的序号,原理图的序号需要和PCB封装一一…...
