一篇文章搞懂二叉树
文章目录
- DP
- 树
- 叶的度
- 树的度
- 节点的层次
- 节点的祖先
- 节点的子孙
- 双亲节点或父节点
- 树的表示
- 孩子兄弟表示法
- 双亲表示法
- 树和非树
- 树的应用
- 二叉树
- 满二叉树
- 完全二叉树
- 推论
- 二叉树的存储
- 以数组的方式
- 以链表的方式
- 堆(Heap)
- 堆的分类
- 大根堆和小根堆的作用
- 二叉树的遍历
- DFS和BFS
DP
动态规划(英语:Dynamic programming,简称 DP)是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。
动态规划常常适用于有重叠子问题和最优子结构性质的问题,并且记录所有子问题的结果,因此动态规划方法所耗时间往往远少于朴素解法。
动态规划有自底向上和自顶向下两种解决问题的方式。自顶向下即记忆化递归,自底向上就是递推。
使用动态规划解决的问题有个明显的特点,一旦一个子问题的求解得到结果,以后的计算过程就不会修改它,这样的特点叫做无后效性,求解问题的过程形成了一张有向无环图。动态规划只解决每个子问题一次,具有天然剪枝的功能,从而减少计算量。
树
树是所有节点的集合,最上面的节点是根,最下面的节点是叶。树的集合就是森林。树是递归定义的,因为每一个节点都可以拆成根+子树。子树又可以拆分,一直拆分,也就是递归了。
叶的度
该节点下面直接相连的节点个数
树的度
整个树中最大的叶的度
节点的层次
从根开始定义起,根为第1层,根的子节点为第2层,以此类推;如果一个树的根为0层的话,那空树只能用-1来表示了。这就是复数了。为了方便表示,让空树等于0,根为1层比较好。本片所用的理论就是根为1层。
节点的祖先
从根到该节点所经分支上的所有节点
节点的子孙
以某节点为根的子树中任一节点都称为该节点的子孙
双亲节点或父节点
若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B
的父节点
树的表示
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,实际中树有很多种表示方式,
如:双亲表示法,孩子表示法、孩子兄弟表示法等等。我们这里就简单的了解其中最常用的孩子
兄弟表示法。
孩子兄弟表示法
typedef int DataType;
struct Node
{struct Node* _firstChild1; // 第一个孩子结点struct Node* _pNextBrother; // 指向其下一个兄弟结点DataType _data; // 结点中的数据域
};
这个树的结构叫:左孩子,右兄弟。
什么意思呢,就是如果这个节点有子节点,也就是该节点的孩子,就让这个节点的左孩子指针保存孩子的地址,如果该节点没用孩子,就指向空,如果该节点的父节点除了该节点还有其他的子节点,就让该节点的右兄弟指向兄弟节点。这里的兄弟只算亲兄弟,也就是同一个父亲的兄弟。
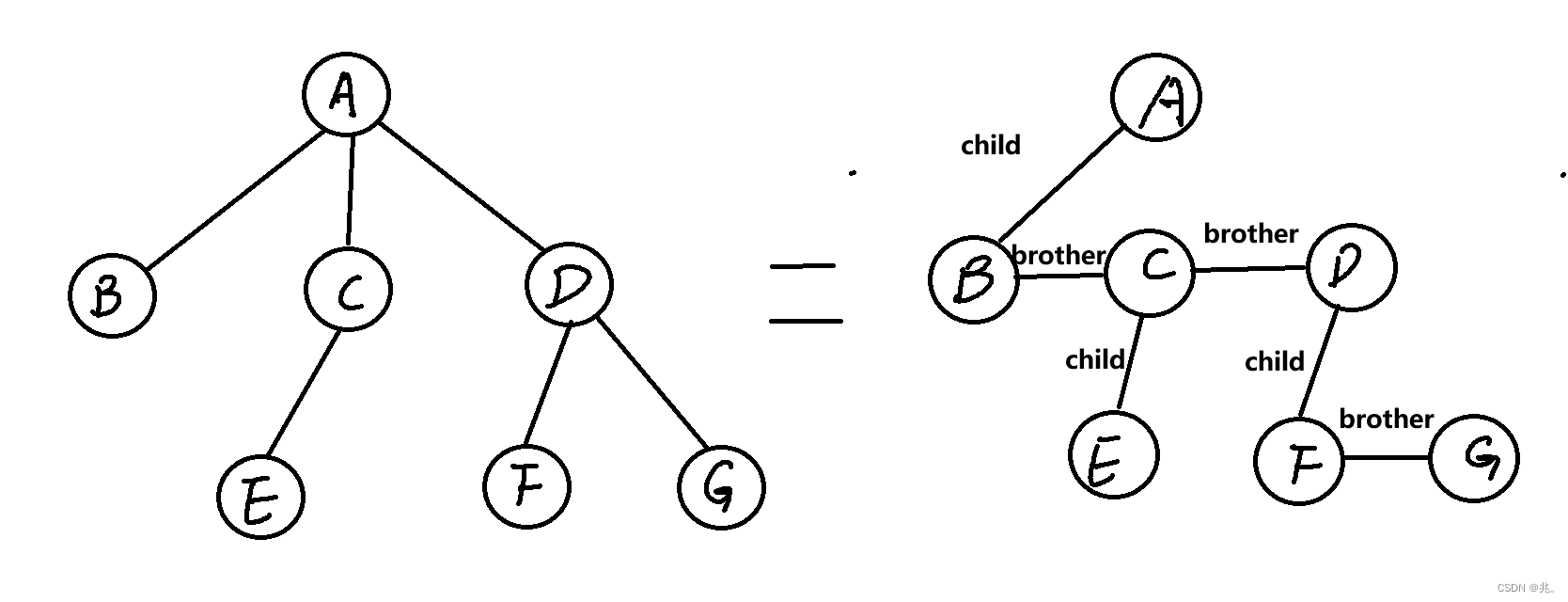
对于一个正常的树状结构来说,需要进一步的转换才能用左孩子右兄弟的方法来表示。就像左边这个树,BCD是A的孩子,A只需要指向他最左边的孩子B就行,然后用B的右兄弟指针连接C,再让C的右兄弟连接D。发现B没有孩子,就让B的左孩子指向空。C的孩子是E,就让左孩子指向E。E既没有孩子,也没有兄弟,左孩子和右兄弟指针都指向空。然后返回上一节点C,再通过C去找D,D有孩子F,D的左孩子就指向F,F还有一个兄弟,就让F的右兄弟指向G。到这里就都连接完了,其他没用的指针都指向空。
双亲表示法
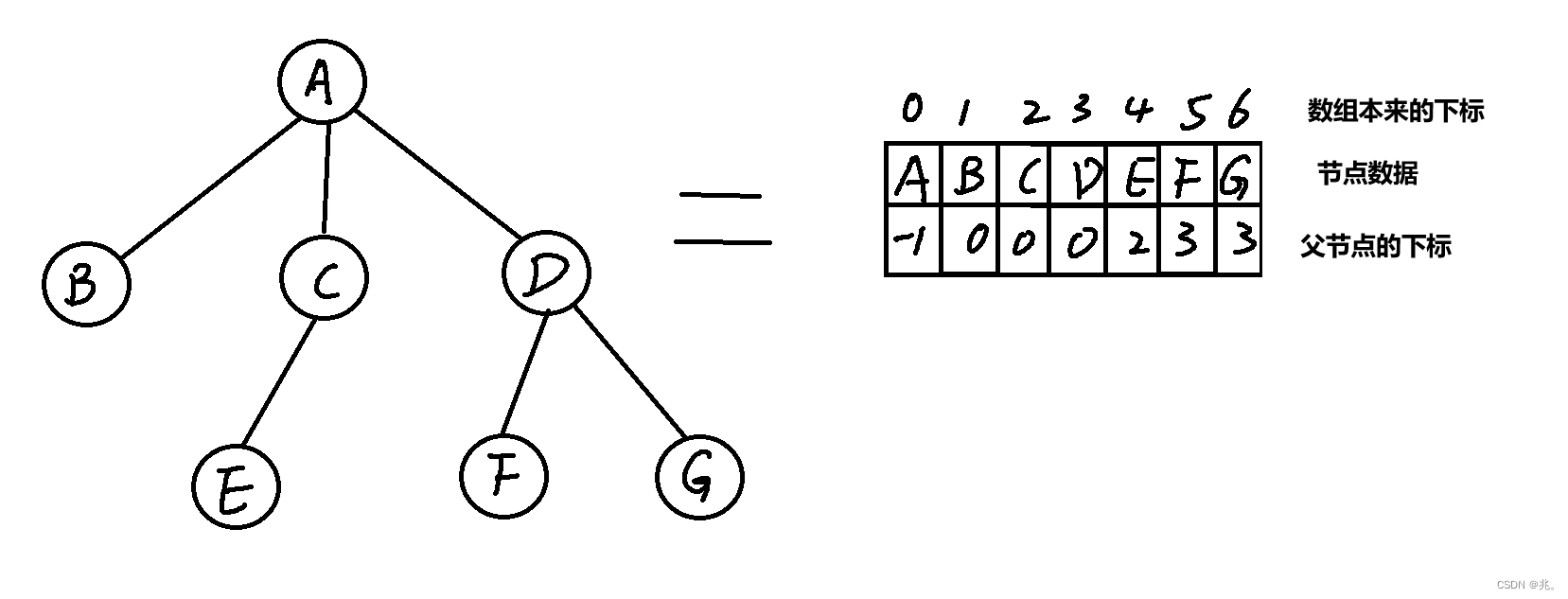
因为一个父亲可以有多个孩子,但是一个孩子只能有一个父亲,所以可以逆向思考,让孩子存父亲节点。
这里的树的结构体要全部存在数组中,就是定义一个指针数组,数组的每个元素都是指针,每个指针指向一个树的节点。
优点是:寻找父节点的题
缺点是:找孩子节点要变量整个数组,也就是整个树。
树和非树
子树不可相交,每个子树仅有一个父节点,一颗树有N个节点,有N-1条边。不能有孤立的点。比如,5个节点的树,一定有4条边。
就是树不能成环,不能有回路,以后学的图的可能有回路,等等
树的应用
目录树,C盘,D盘了,文件夹就是节点,文件可能是节点可能是叶子
二叉树
二叉树是特殊的树,就是度为2的树。每个节点最多两个孩子,也可以是空节点,那就是叶子
满二叉树
就是每个节点都是满的,除了叶子。根节点为1
结论:一个完全二叉树的层次为k,那么总的节点个数就是(2k-1),等比数列求和
每一层的节点个数就是2k-1 个
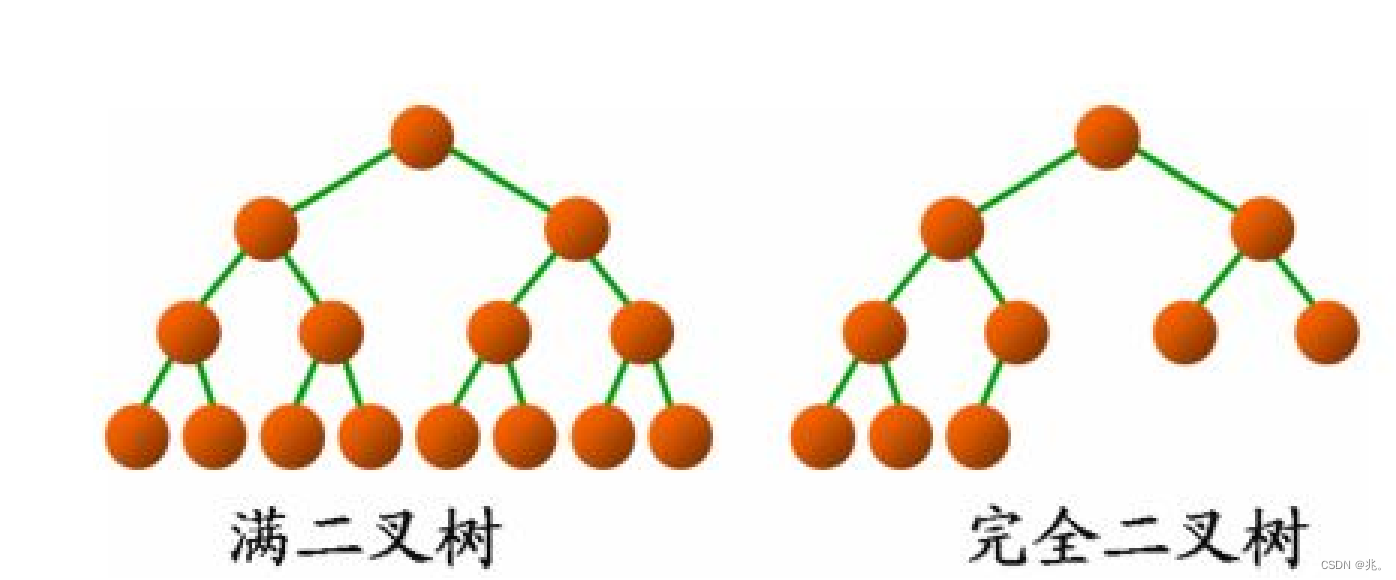
完全二叉树
完全二叉树的最底层可以不完整,但是必须从左到右连续。最后一层不满,但连续。满二叉树是特殊的完全二叉树。
树–>二叉树–>完全二叉树–>满二叉树
推论
二叉树的(叶子节点的个数)是(度为2的节点的个数+1)。叶节点的个数是有俩孩子节点个数的多一个。
如果一个二叉树有N个节点,高度是h。
- 对于满二叉树来说:2*h-1=N;h=log2(N+1)
- 对于完全二叉树来说:2*h -1-X=N。(0<=x<=2h-1-1) ,log2N <= h <=log2(N + 1)
例题:
1. 某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为( B )
A 不存在这样的二叉树
B 200
C 198
D 199
2.在具有 2n 个结点的完全二叉树中,叶子结点个数为( A )
A n
B n+1
C n-1
D n/2
3.一棵完全二叉树的节点数位为531个,那么这棵树的高度为( B )
A 11
B 10
C 8
D 12
二叉树的存储
以数组的方式
从根节点开始在数组下标为0的地方,然后从左到右依次填入数组,对于完全二叉树来说。
- 若一个父节点的下标是i,那么孩子的下标分别是:2i+1和2i+2。i=4.2i+1=9,2i+2=10。
- 若一个子节点的下标是i,那么父节点下标是:(i-1)/2。(6-1)/2=5/2=2. (5-1)/2=4/2=2。
以链表的方式
链表的方式大概有两种:二叉链表,三叉链表。
二叉链表,就是有两个子节点指针的链表,三叉链表就是有两个子节点child指针,还有一个父节点parent指针。二叉链表,应用的比较多。三叉树一般应用在平衡树,红黑树等等。
// 二叉链
struct BinaryTreeNode
{struct BinTreeNode* pLeft; // 指向当前节点左孩子struct BinTreeNode* pRight; // 指向当前节点右孩子BTDataType _data; // 当前节点的值
}
// 三叉链
struct BinaryTreeNode
{struct BinTreeNode* pParent; // 指向当前节点的父亲struct BinTreeNode* pLeft; // 指向当前节点左孩子struct BinTreeNode* pRight; // 指向当前节点右孩子BTDataType _data; // 当前节点的值
};
堆(Heap)
堆就是完全二叉树,用数组来储存。
堆的分类
- 大堆(大根堆)
每个父节点都大于等于子节点。左右孩子大小不规定。
- 小堆(小根堆)
每个父节点都小于等于子节点。左右孩子大小不规定。
大根堆和小根堆的作用
根(堆顶)是最大值或最小值。应用在堆排序中。
例题:
1.下列关键字序列为堆的是:(A)
A 100,60,70,50,32,65
B 60,70,65,50,32,100
C 65,100,70,32,50,60
D 70,65,100,32,50,60
E 32,50,100,70,65,60
F 50,100,70,65,60,32
二叉树的遍历
由于二叉树是一个非线性结构,不同于以往的单链表或者数组,只能从头到尾,或者从尾到头的遍历顺序。
二叉树可分为左子树、右子树、根三部分。根据三个部分的先后顺序划分,有三种分法:
- 前序(先根遍历):根->左子树->右子树
- 中序(中根遍历):左子树->根->右子树
- 后序(后根遍历):左子树->右子树->根
DFS和BFS
深度优先搜索算法(英语:Depth-First-Search,DFS)是一种用于遍历或搜索树或图的算法。其过程简要来说是对每一个可能的分支路径深入到不能再深入为止,而且每个结点只能访问一次.
因发明「深度优先搜索算法」,约翰 · 霍普克洛夫特与罗伯特 · 塔扬在1986年共同获得计算机领域的最高奖:图灵奖。
广度优先搜索算法(Breadth-First Search,缩写为 BFS),又称为宽度优先搜索,是一种图形搜索算法。简单的说,BFS 是从根结点开始,沿着树的宽度遍历树的结点。如果所有结点均被访问,则算法中止。
又因为二叉树结构的特殊性,有层数之分,根据探索的层数有两种分法:深度优先遍历,广度优先遍历
其中深度优先遍历就是:前中后序这三种方式
广度优先遍历是层序。所谓的层序就是一层层的挨着访问。从左到右。
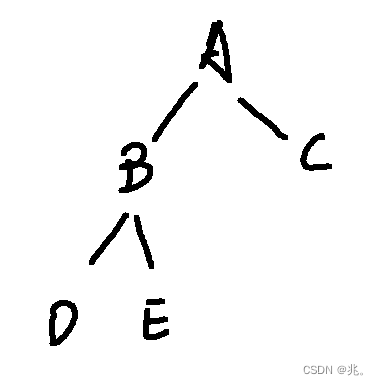
举个例子:
-
前序:A->B->D->NULL->NULL->E->NULL->NULL->C->NULL->NULL
一般方便表示,不会写NULL,也就是ABDEC.
-
中序:NULL->D->NULL->B->NULL->E->NULL->A->NULL->C->NULL
-
后序:NULL->NULL->D->NULL->NULL->E->B->NULL->NULL->C->A
-
层序:A->B->C->D->E->NULL->NULL->NULL->NULL->NULL->NULL
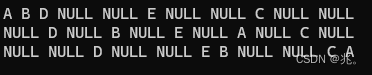
大概是什么意思呢?拿中序来说,拿到这棵树,第一个节点也就是根,但是不会访问他的值,因为中序访问就是先访问左子树,对于A这棵树而言,左子树是以B为根的子树,但是这时候不能访问B的值,因为对于B而言,D才是B的左子树,对于D而言,左子树为空,返回NULL(这也就是中序第一个NULL的来源)。然后返回D节点,D是以D为根的子树的根,D的左子树已经访问完了,所以要访问D,然后访问D这棵树的右子树,右子树还是空,返回NULL。以D为根的子树才彻底访问完毕。D又是B的左子树,以B为根的子树的左子树访问完,才访问根B的值。接着是B的右子树E。以E为根的子树还要先访问左子树。。。。。。。
不难发现,中序是先沿着左子树这条路,一直找到了D的左子树NULL才停止访问。然后返回上级D这条岔路口走右子树。再返回D的上级B岔路口走右子树。
随着程序的运行,一开始就先找最深的地方,也就是深度优先遍历。走到空,无路可走了,才退回来。
所以深度优先适合数组、图,这种量大的遍历。
实现深度优先一般用递归,栈。
实现广度优先用队列。
相关文章:

一篇文章搞懂二叉树
文章目录 DP 树叶的度树的度节点的层次节点的祖先节点的子孙双亲节点或父节点 树的表示孩子兄弟表示法双亲表示法树和非树树的应用 二叉树满二叉树完全二叉树推论二叉树的存储以数组的方式以链表的方式堆(Heap)堆的分类大根堆和小根堆的作用 二叉树的遍历DFS和BFS DP 动态规划…...

python——__future__模块
__future__模块是Python的一个特殊内建模块,它提供了一种方式来让程序员在当前版本的Python中使用未来版本的语言特性,从而帮助代码实现向前兼容。这意味着,即使你正在使用的是旧版本的Python,也可以通过导入__future__模块中的某…...
开源一个工厂常用的LIMS系统
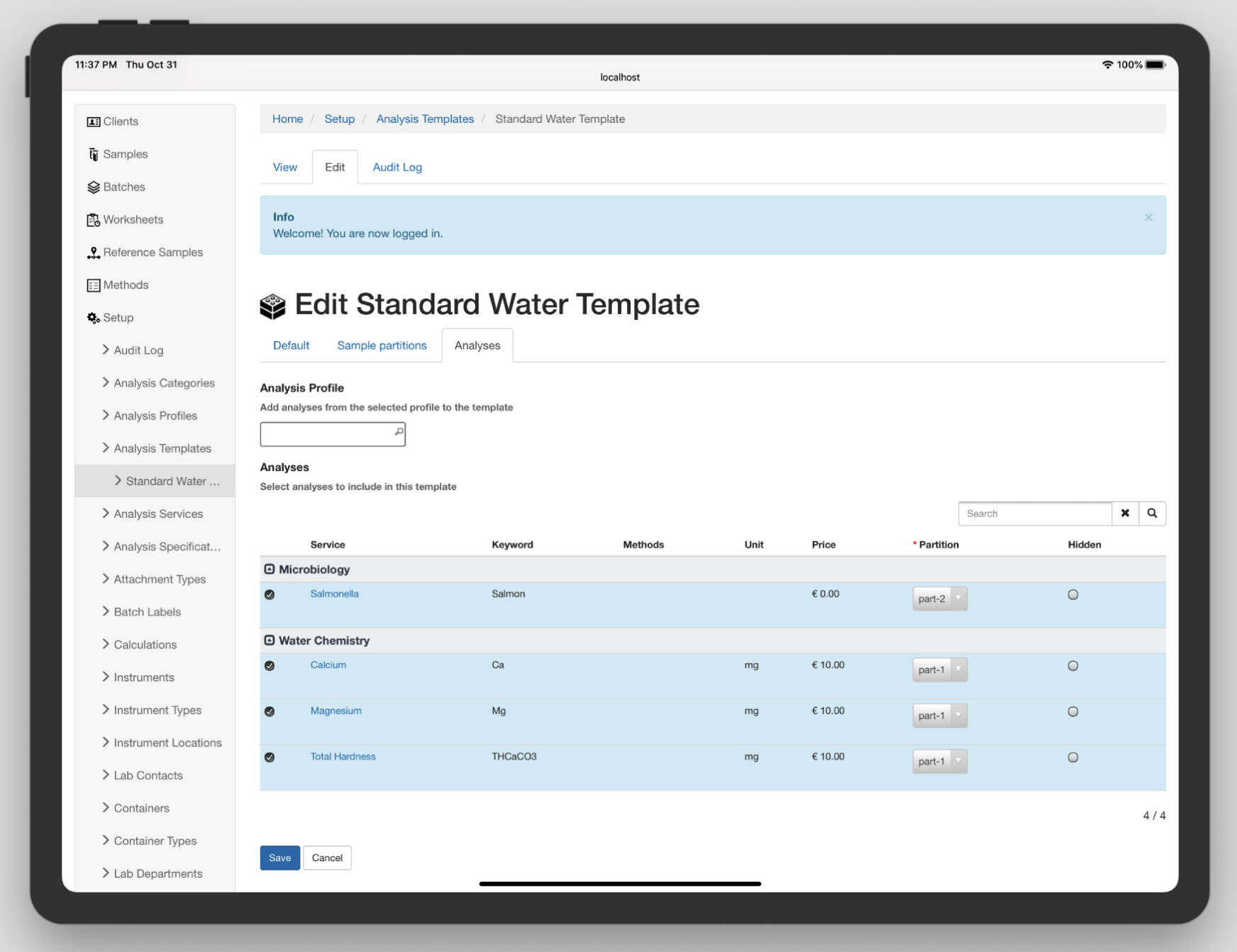
Senaite是一款强大且可靠的基于Web的LIMS/LIS系统,采用Python编写,构建在Plone CMS基础架构之上。该系统处于积极开发阶段,在灵活的定制空间中为开发人员提供了丰富的功能。其中,Senaite在处理REST的JSON API上做得出色࿰…...

SpringBoot项目中redis序列化和反序列化LocalDateTime失败
实体类中包含了LocalDateTime 类型的属性,把实体类数据存入Redis后变成这样: 此时,存入redis不会报错,但是从redis获取的时候,会报错: com.fasterxml.jackson.databind.exc.InvalidDefinitionException: Ca…...

linux怎么查询远程管理卡型号
在Linux中,要查询远程管理卡(通常是服务器主板上的集成芯片,如iDRAC、iLO、BMC等)的型号,可以使用一些特定厂商的工具,或者通过IPMI(Intelligent Platform Management Interface)来实…...
西储大学数据集学习
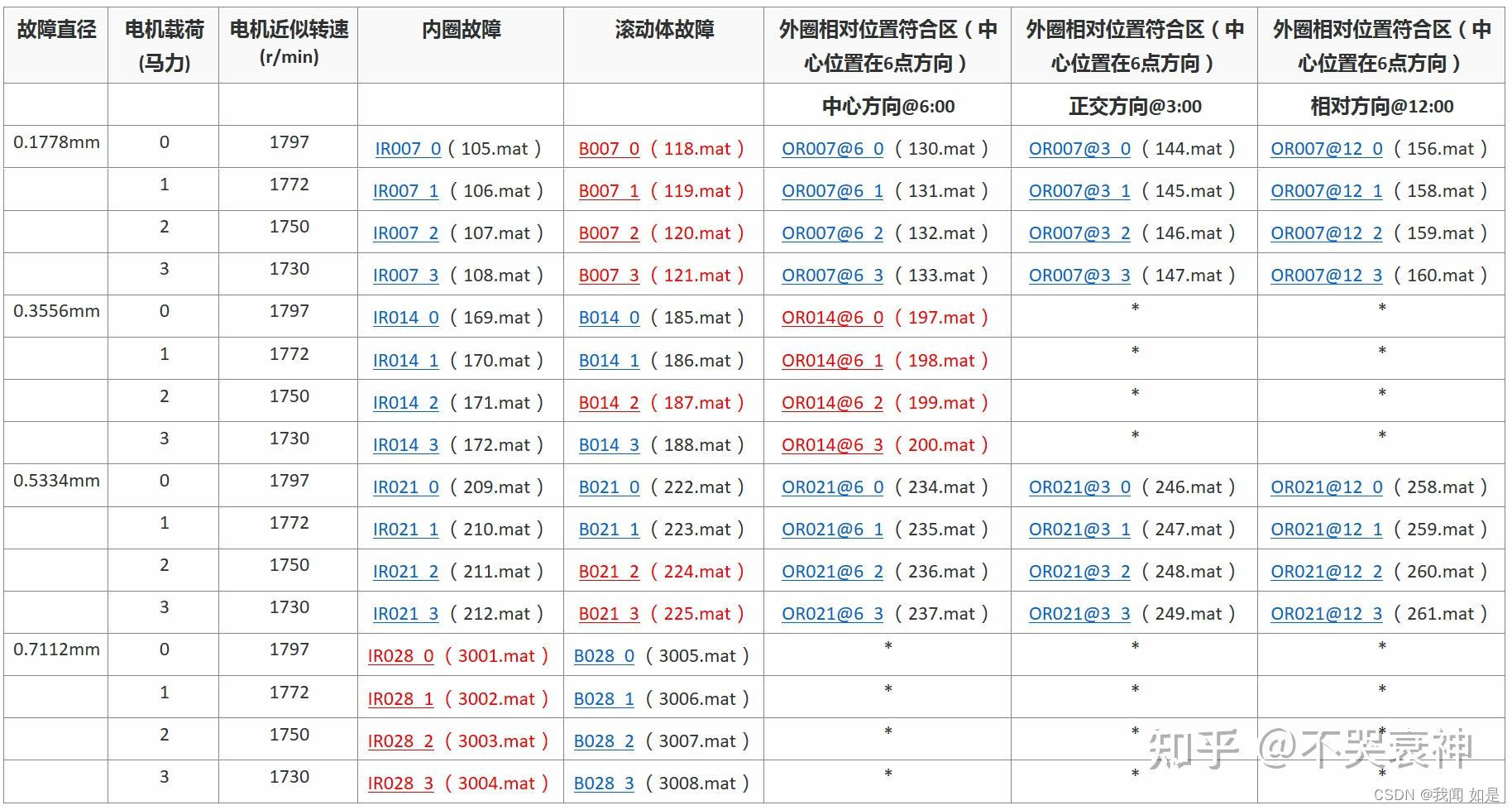
数据集下载地址:CWRU凯斯西储大学轴承数据数据集——附:下载链接_西储大学轴承数据集下载-CSDN博客 最近研究故障诊断,先对使用比较多的西储大学数据集研究。以资料【1】中的内容展开研究。 1、轴承的结构 轴承分为外圈、内圈、保持架和滚珠…...
《web应用技术》第九次作业
一、将前面的代码继续完善功能 1.采用XML映射文件的形式来映射sql语句; <?xml version"1.0" encoding"UTF-8" ?> <!DOCTYPE mapper PUBLIC "-//mybatis.org//DTD Mapper 3.0//EN" "http://mybatis.org/dtd/mybatis…...

dockerfile关键字
参考:59_Dockerfile保留字简介_哔哩哔哩_bilibili FROM 作用:指定基础镜像,即在这个基础镜像上构建新镜像,如下所示,表示在ubuntu20.04镜像的基础上构建新镜像 FROM ubuntu:20.04 MAINTAINER 作用:镜像…...
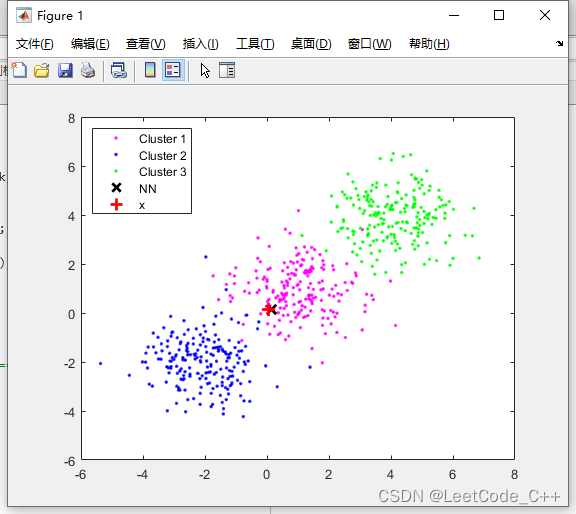
MATLAB分类与判别模型算法: 快速近邻法(FastNN)分类程序【含Matlab源码 MX_005期】
算法思路介绍: 1. 数据准备阶段: 生成一个合成数据集 X,其中包含三个簇,每个簇分布在不同的区域。 定义聚类层数 L 和每个层次的子集数量 l。 2. 聚类阶段: 使用K均值聚类算法将初始数据集 X 分成 l 个簇。…...

css卡片翻转 父元素翻转子元素不翻转效果
css卡片翻转 父元素翻转子元素不翻转效果 vue <div class"moduleBox"><div class"headTitle"><span class"headName">大额案例</span></div><div class"moduleItem"><span class"module…...

解决文件传输难题:如何绕过Gitee的100MB上传限制
引言 在版本控制和代码托管领域,Gitee作为一个流行的平台,为用户提供了便捷的服务。然而,其对单个文件大小设定的100MB限制有时会造成一些不便。 使用云存储服务 推荐理由: 便捷性:多数云存储服务如: Dro…...

零基础学Java第二十三天之网络编程Ⅱ
1. InetAddress类 用来表示主机的信息 练习: C:\Windows\system32\drivers\etc\ hosts 一个主机可以放多个个人网站 www.baidu.com/14.215.177.37 www.baidu.com/14.215.177.38 www.taobao.com/183.61.241.252 www.taobao.com/121.14.89.253 2. Socket 3.…...

【HarmonyOS尝鲜课】- 前言
面向人群 本课程适用于HarmonyOS应用开发的初学者。 有无经验的开发者都可以轻松掌握ArkTS语言声明式开发范式,体验更简洁、更友好的HarmonyOS应用开发旅程。 什么是HarmonyOS HarmonyOS(鸿蒙操作系统)是由华为技术有限公司开发的全场景分…...

phpstudy配置网站伪静态
apache的伪静态写法: RewriteEngine On RewriteCond % {REQUEST_FILENAME} !-f RewriteCond % (REQUEST_FILENAME) !-d RewriteRule ^(.*)$ indexp?/$1 [QSA, PT,L] nginx写法: location / { index index.html index.php; #autoindex on; if(!…...

浅谈traceroute网络诊断工具
traceroute 是一个网络诊断工具,用于跟踪和显示数据包从源主机到目标主机所经过的每一跳(路由器)的路径。它能够帮助用户识别网络路径中的瓶颈和故障点。traceroute 的工作原理主要基于 ICMP(Internet Control Message Protocol&a…...
)
Java数据结构与算法(红黑树)
前言 红黑树是一种自平衡二叉搜索树,确保在插入和删除操作后,树的高度保持平衡,从而保证基本操作(插入、删除、查找)的时间复杂度为O(log n)。 实现原理 红黑树具有以下性质: 每个节点要么是红色&#…...

SpringBoot RPM制作
安装依赖 [root20240423-instance4 ~]# yum install rpmdevtools2.初始化目录 [root20240423-instance4 ~]# rpmdev-setuptree [root20240423-instance4 ~]# tree rpmbuild/ rpmbuild/ ├── BUILD ├── RPMS ├── SOURCES ├── SPECS └── SRPMS5 directories, 0 …...

专转本上岸别太老实做这三件事
如果你专转本上岸,千万不要当老实人去做这三件事,真的没有必要,不但浪费时间,还会让你提前进入对未来的迷茫期。建议转本人们一定要知道,首先就是不要过度关注学分。因为转本上岸只有两年,我们属于大三&…...
)
Cisco网络工程师和网络安全视频教程(完整版)
0001.IT技术包括的技能 0002.课程目标.mp4 0003.Internet示意图.m 0004.局域网和广域网区 0005.服务器客户机mp4 0006.应用层和表示层.m.. 0007.会话层.mp4 0008.传输层.mp4 0009.网络层数据链路层 0010.OSI参考模型和网 0011.普换法排错.mp4 0012.OSI参考模型和网. 0013.网线和…...

如何在一个 JavaScript 文件中引入另一个 JavaScript 文件
在早期版本的 JavaScript 中,没有提供原生的模块导入功能,因此开发者们尝试过各种不同的方法来解决这个问题。然而,自 2015 年 (ES6) 以来,JavaScript 引入了 ES6 模块标准,这使得在 Node.js 中导入模块变得更加规范。现代浏览器也广泛支持这一标准。 为了与旧版浏览器兼…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...
