支持向量回归删除异常值Python
1、支持向量回归(SVR)原理
支持向量回归(Support Vector Regression,SVR)不仅可以用于预测,还可以用于异常值检测。其基本思路是训练一个回归模型,通过对每个数据点进行预测,并计算其预测残差,来判断该数据点是否为异常值。
在SVR中,我们通过最大化预测出错的容忍度(margin)来寻找最优解。具体地,我们希望找到一个超平面,使得所有数据点到该超平面的距离都大于等于一定的阈值(margin)。对于线性回归模型,该超平面为:
w^T * x + b = 0
其中,w是超平面法向量,b是偏置项,x是输入数据。对于一个输入数据x_i,其距离超平面的距离为:
y_pred_i - y_i = (w^T * x_i + b) - y_i
其中,y_pred_i是该数据点的预测值,y_i是该数据点的真实值。我们定义预测残差为绝对值:
r_i = abs(y_pred_i - y_i)
那么,如果某个数据点的预测残差(r_i)大于某个阈值,则被视为异常值,否则视为正常值。
在实际操作中,我们需要指定SVR的一些超参数,例如核函数类型、核函数参数、惩罚系数等。这些超参数对于SVR的性能有很大的影响,需要根据具体问题进行调整。
2、关键函数svr.fit函数参数
sklearn.svm.SVR中fit函数常用参数如下:
X: 训练数据X,必选参数,形状为(n_samples, n_features)。y: 目标值y,必选参数,形状为(n_samples,)。sample_weight: 样本权重,可选参数,形状为(n_samples,),默认每个样本的权重相等。C: 惩罚系数,可选参数,默认为1.0,一般取值为(0, +∞)之间的数。C越小,模型越简单;C越大,模型越复杂。调整C的值可以防止过拟合或欠拟合的问题。kernel: 核函数,可选参数,默认为’rbf’,表示高斯核函数。常用的核函数还有’linear’线性核函数、'poly’多项式核函数、‘sigmoid’ Sigmoid核函数。核函数的选择决定了模型的复杂度和拟合能力。degree: 多项式核函数的次数,可选参数,默认为3。gamma: 核函数系数,可选参数,默认为’scale’,表示使用1 / (n_features * X.var())作为gamma值。也可以设置为’auto’或一个数值。coef0: 核函数的截距,可选参数,默认为0。epsilon: SVR中的ε,可选参数,默认为0.1。控制了对误差的容忍度。如果预测值与真实值的差小于ε,该点就被视为预测正确。shrinking: 是否使用启发式(Hearst)方法来加速计算,可选参数,默认为True。建议保持默认值。tol: 迭代终止条件,可选参数,默认为1e-3。如果模型收敛后两次迭代的损失函数之差小于该值,则终止训练。max_iter: 最大迭代次数,可选参数,默认为-1,表示没有限制。如果收敛前达到该值,则提前终止训练。cache_size: 核函数缓存大小,可选参数,默认为200MB。
需要根据具体的情况,调整SVR的超参数以获得更好的性能和效果。
3、完整代码
import pandas as pd
from sklearn.svm import SVR# 加载数据
data = pd.read_csv('data.csv')# 训练SVR模型
X = data.index.values.reshape(-1, 1)
y = data['value'].values.reshape(-1, 1)
svr = SVR(kernel='rbf', gamma='scale', C=1.0, epsilon=0.1)
svr.fit(X, y)# 计算每个数据点的预测偏差
y_pred = svr.predict(X)
residuals = abs(y - y_pred)# 计算偏差的标准差
std_dev = residuals.std()# 计算阈值
threshold = 3 * std_dev# 找到异常值
mask = (residuals <= threshold).flatten()
clean_data = data.loc[mask]# 输出结果
print(clean_data)
测试报错:
Reshape your data either using array.reshape(-1, 1) 。
dataframe数据需要转换为array。
经测试:
X = df['X'].values.reshape(-1, 1)
y = np.array(df['y'])
测试结果:
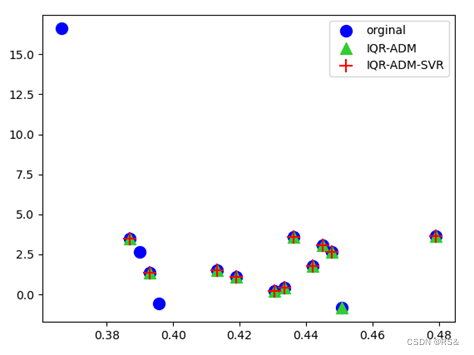
相关文章:

支持向量回归删除异常值Python
1、支持向量回归(SVR)原理 支持向量回归(Support Vector Regression,SVR)不仅可以用于预测,还可以用于异常值检测。其基本思路是训练一个回归模型,通过对每个数据点进行预测,并计算…...
手把手开发一门程序语言JimLang (2)
根据爱因斯坦的相对论,物体的质量越大,时间过得越快,所以托更对于我的煎熬,远远比你们想象的还要痛苦…今天给大家来盘硬菜,也是前些时日预告过的JimLang的开发过程… Let’s go !!! 语法及解析 JimLang.g4 这里我们…...
DSF深度搜索时到底是如何回溯的(小tip)
这一段让我迷了两次,为什么回溯的时候,恢复了最后一位,往上递归一层之后,把最后一位填在它前一位,但是原本的前一位没有恢复,最后一位要怎么办?其实这还是递归没明白 也就是这一步是如何实现的 …...
:打包发布)
Rust Web入门(八):打包发布
本教程笔记来自 杨旭老师的 rust web 全栈教程,链接如下: https://www.bilibili.com/video/BV1RP4y1G7KF?p1&vd_source8595fbbf160cc11a0cc07cadacf22951 学习 Rust Web 需要学习 rust 的前置知识可以学习杨旭老师的另一门教程 https://www.bili…...

synchronize优化偏向锁
偏向锁 轻量级锁在没有竞争时(只有自己一个线程),仍然会尝试CAS替换mark word; 会造成一定的性能的损耗; JDK6之中引入了偏向锁进行优化,第一次使用时线程ID注入到Mark word中,之后重入不再进…...

算法习题之动态规划
动态规划习题1 打印n层汉诺塔从最左边移动到最右边的全部过程习题2 给你一个栈,请你逆序这个栈,不能申请额外的数据结构,只能使用递归函数。 如何实现?习题3 打印一个字符串的全部子序列,打印一个字符串的全部子序列,…...

顺序表【数据结构】
文章目录:star2:1. 顺序表概念:star2:2. 框架3. 基本功能3.1 头文件:star:3.2 初始化:star:3.3 扩容:star:3.4 打印:star:3.5 尾插:star:3.6 头插:star:3.7 尾删:star:3.8 头删:star:3.9 指定插入:star:3.10 指定删除:star:3.11 查找:star2:3.12 注意事项4. 顺序表的缺点&#…...
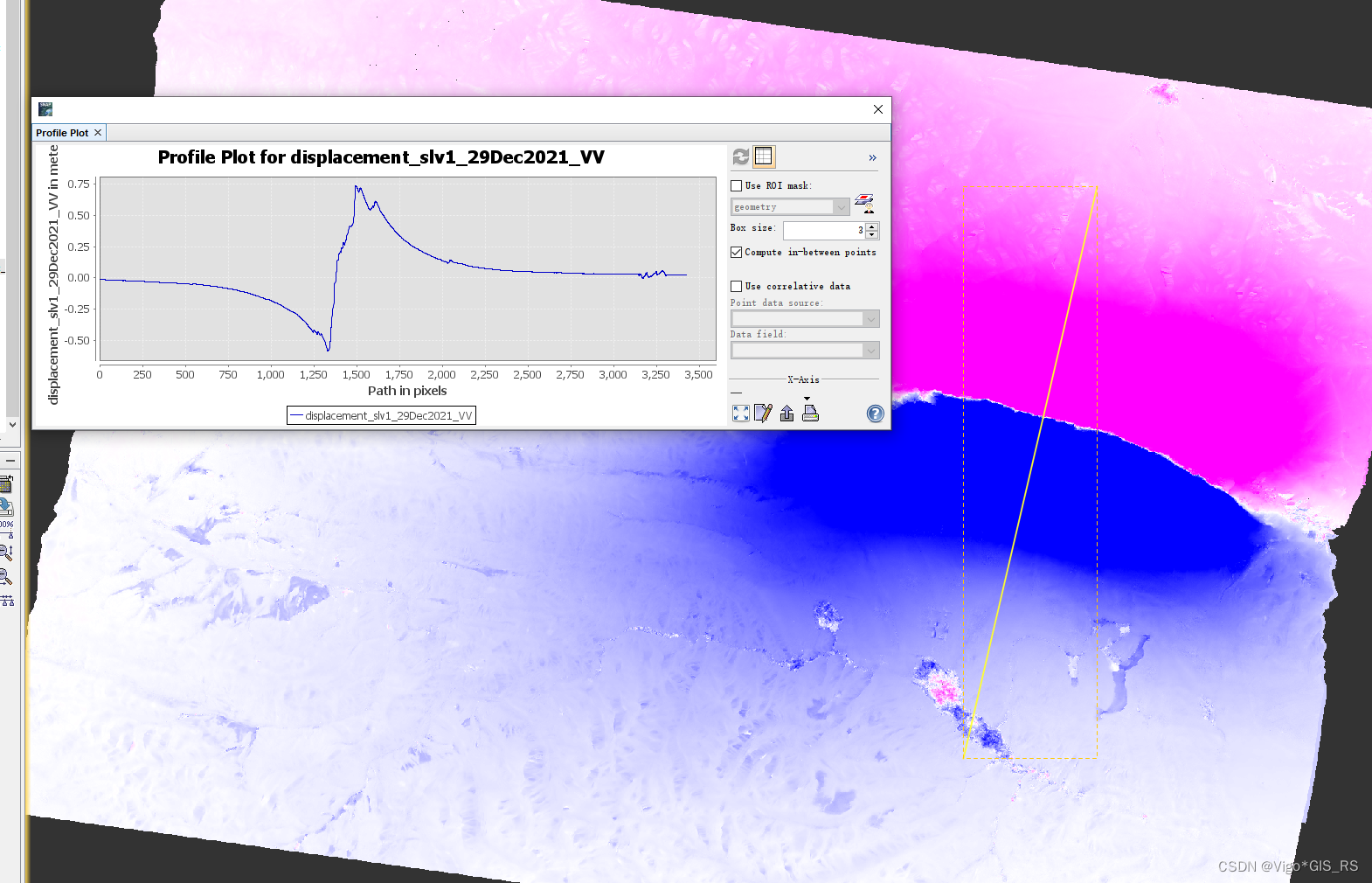
SNAP中根据入射角和干涉图使用波段计算器计算垂直形变--以门源地震为例
SNAP中根据入射角和相干图使用波段计算器计算垂直形变--以门源地震为例0 写在前面1 具体步骤1.1 准备数据1.2 在SNAP中打开波段运算Band Maths1.3 之前计算的水平位移displacement如下图数据的其他处理请参考博文在SNAP中用sentinel-1数据做InSAR测量,以门源地震为例…...
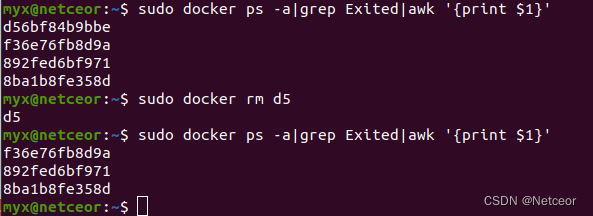
Ubuntu20.04中Docker安装与配置
一、安装 1、卸载可能存在的旧版本 sudo apt-get remove docker docker-engine docker-ce docker.io2、更新apt包索引 sudo apt-get update显示“正在读取软件包列表… 完成” 3、安装以下包以使apt可以通过HTTPS使用存储库(repository) sudo apt-get install -y apt-tran…...

pytorch权值初始化和损失函数
pytorch权值初始化和损失函数 权值初始化 梯度消失与爆炸 针对上面这个两个隐藏层的神经网络,我们求w2的梯度 可以发现,w2的梯度与H1(上一层网络的输出)有很大的关系,当h1趋近于0时,w2的梯度也趋近于0&am…...

maven将jar文件上传至本地仓库及私服
maven官方仓库有些依赖并不存在,现在项目都是maven直接获取jar,当maven获取不到时,需要我们把jar上传至maven仓库。已 ImpalaJDBC41.jar 文件为例,如:希望上传后,设置的依赖为:<dependency&g…...

前端学习第三阶段-第1、2章 JavaScript 基础语法
01第一章 JavaScript网页编程课前导学 1-1 JavaScript网页编程课前导学 02第二章 JavaScript 基础语法 2-1 计算机基础和Javascript介绍 01-计算机基础导读 02-编程语言 03-计算机基础 04-JavaScript初识导读 05-初始JavaScript 06-浏览器执行JS过程 07-JS三部分组成 08-JS三种…...

hibernate学习(二)
hibernate学习(二) 一、hibernate常见配置: 1.XML提示问题配置: 二、hibernate映射的配置: (1)class标签的配置: 标签用来建立类与表之间的映射关系属性: 1.name&…...
平安银行LAMBDA实验室负责人崔孝林:提早拿到下一个计算时代入场券
量子前哨重磅推出独家专题《“量子”百人科学家》,我们将遍访全球探索赋能“量子”场景应用的百位优秀科学专家,从商业视角了解当下各行业领域的“量子”最新研究成果,多角度、多维度、多层面讲述该领域的探索历程,为读者解析商业…...

linux下进不去adb
linux 进不去adb cat /sys/kernel/debug/usb/devices 查看是否有adb口 首先查看adb是否被识别成串口 option 如果被识别成串口 方法1: https://patchwork.kernel.org/project/linux-usb/patch/20180723140220.7166-1-romain.izard.progmail.com/ diff --git a/dri…...

【SPSS】多因素方差分析详细操作教程(附案例实战)
🤵♂️ 个人主页:@艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞👍🏻 收藏 📂加关注+ 目录 方差分析概述 多因素方差分析原理...
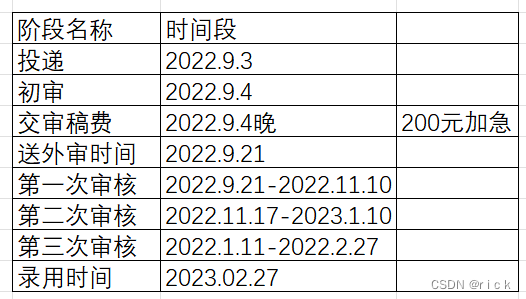
我的投稿之旅
一、铁道科学与工程学报选择这个期刊的原因是:感觉影响因子较低,而且实验室有师兄师姐中过这个期刊,所以抱着试一试的心态投了。投稿之前需要去官网注册账号由于方向不一致,被退稿了“您的稿件内容不属于本刊刊载范畴,…...
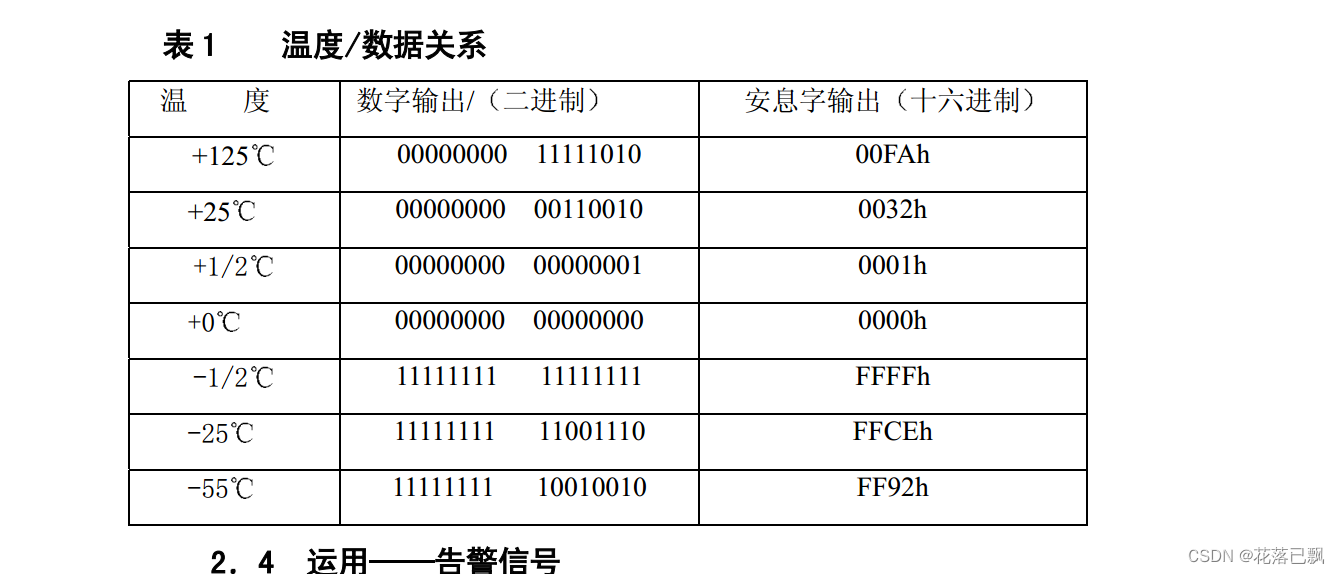
51单片机DS18B20的使用
文章目录前言一、DS18B20介绍二、单总线协议三、DS18B20引脚说明四、DS18B20程序编写1.DS18B20复位函数2.DS18B20存在检测3.DS18B20读取一个bit和一个byte函数4.DS18B20写一个字节函数5.开始温度转换函数6.DS18B20初始化函数7.DS18B20读取温度函数五、代码测试总结前言 本篇文…...
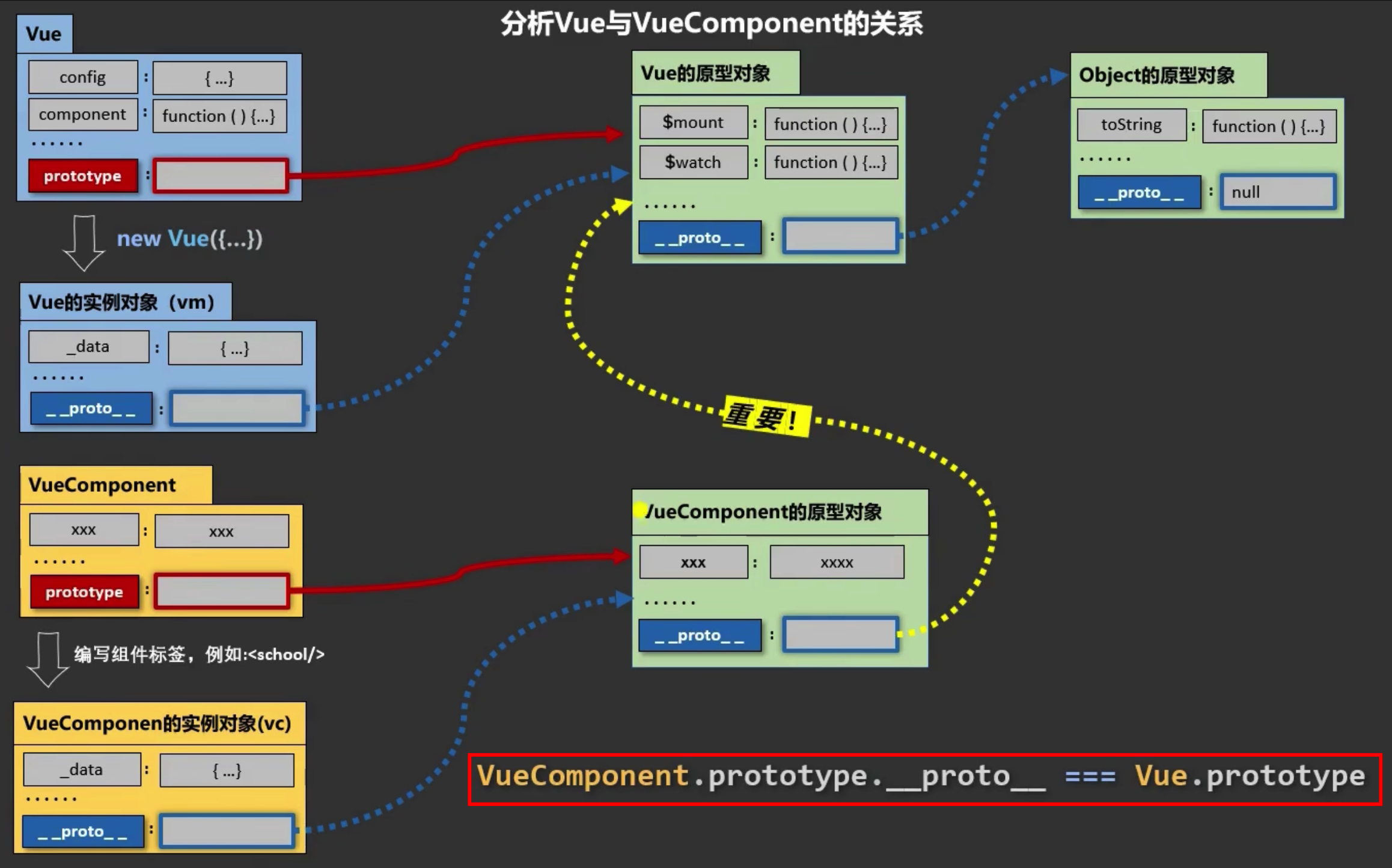
Vue组件原理知识(1)
Vue 组件知识整理(1)文章目录Vue 组件知识整理(1)一、组件介绍1.1 传统方式与组件方式编写应用对比二、组件使用2.1 非单文件组件的使用**1. 组件的创建****2. 组件的注册****3. 组件的使用****4. Vue中使用组件的三大步骤总结***…...

Linux:IO库函数
目录标准库IO函数一、fopen二、fwrite三、fread四、fseek五、fclose在编写程序时,离不开IO操作,最常见的IO操作就是用printf函数进行打印,本文主要介绍的是封装后的IO库函数。 标准库IO函数 常使用的IO库函数如下: 函数作用fop…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...
