Thinkphp3.2.3网站后台不能访问如何修复
我是使用Thinkphp3.2.3新搭建的PHP网站,但是网站前台可以访问,后台访问出现如图错误:

由于我使用的Hostease的Linux虚拟主机产品默认带普通用户权限的cPanel面板,对于上述出现的问题不清楚如何处理,因此联系Hostease的咨询了Hostease技术支持,寻求帮助解决此问题。根据技术的回复告知,上述该问题是由于网站当前的PHP版本过高导致,他们告知当前我使用的是PHP8.1版本的,将PHP版本切换为8.0以下的7.4后访问正常。
他们是到主机cPanel面板--Selete php Version 或者 多PHP编辑器 中进行切换的PHP版本。
相关文章:

Thinkphp3.2.3网站后台不能访问如何修复
我是使用Thinkphp3.2.3新搭建的PHP网站,但是网站前台可以访问,后台访问出现如图错误: 由于我使用的Hostease的Linux虚拟主机产品默认带普通用户权限的cPanel面板,对于上述出现的问题不清楚如何处理,因此联系Hostease的…...

Golang 如何使用 gorm 存取带有 emoji 表情的数据
Golang 如何使用 gorm 存取带有 emoji 表情的数据 结论:在 mysql 中尽量使用 utf8mb4,不要使用 utf8。db报错信息:Error 1366 (HY000): Incorrect string value: \\xE6\\x8C\\xA5\\xE7\\xAC\\xA6...根本原因:emoji 4个字节&#x…...
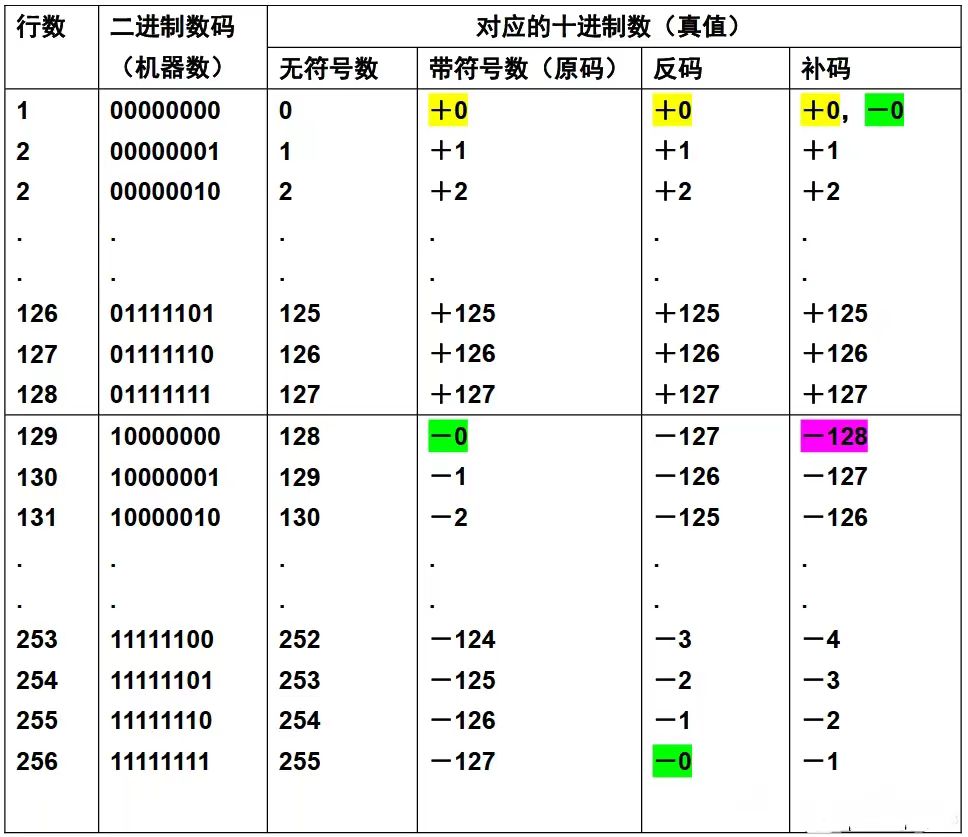
计算机算法中的数字表示法——原码、反码、补码
目录 1.前言2.研究数字表示法的意义3.数字表示法3.1 无符号整数3.2 有符号数值3.3 二进制补码(Twos Complement, 2C)3.4 二进制反码(也称作 1 的补码, Ones Complement, 1C)3.5 减 1 表示法(Diminished one System, D1)3.6 原码、反码、补码总结 1.前言 昨天有粉丝让我讲解下定…...
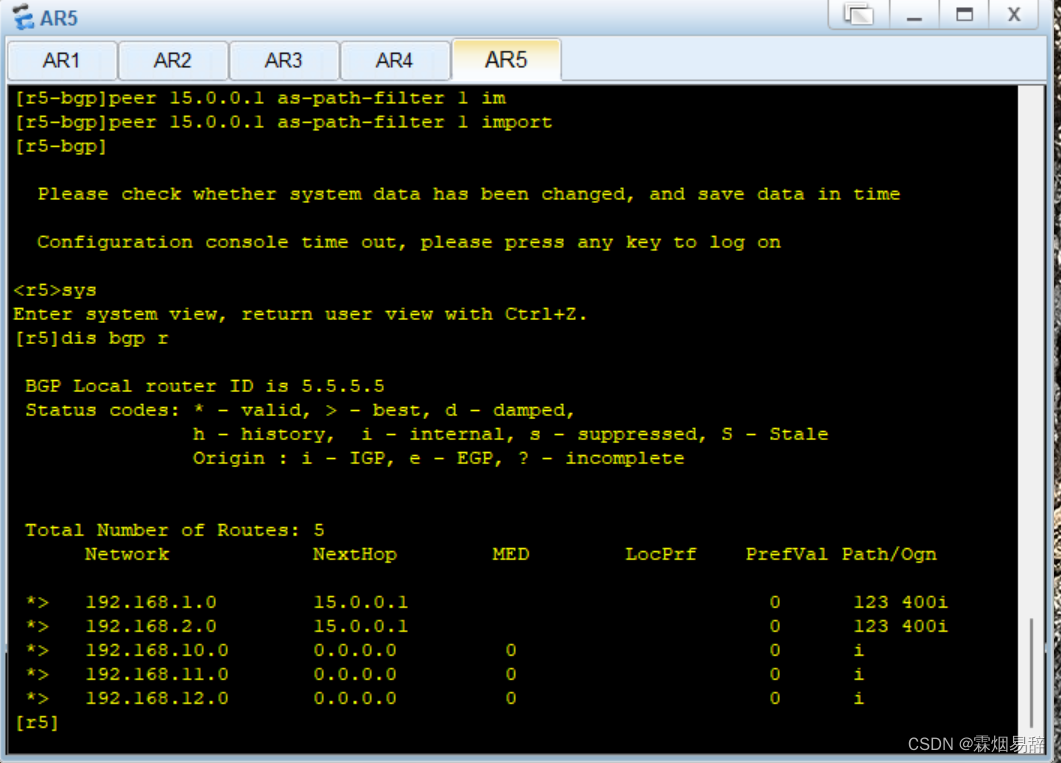
BGP策略实验
一、实验要求 二、实验分析 1.先配置IP 2.再配置BGP 3.配置BGP策略 三、实验过程 要求 1. [r4]ip ip-prefix aa permit 192.168.10.0 24 [r4]route-policy aa permit node 10 [r4-route-policy]if-match ip-prefix aa [r4-route-policy]apply preferred-value 100 [r4]rout…...

目标检测 | R-CNN、Fast R-CNN与Faster R-CNN理论讲解
☀️教程:霹雳吧啦Wz ☀️链接:https://www.bilibili.com/video/BV1af4y1m7iL?p1&vd_sourcec7e390079ff3e10b79e23fb333bea49d 一、R-CNN R-CNN(Region with CNN feature)是由Ross Girshick在2014年提出的,在PAS…...
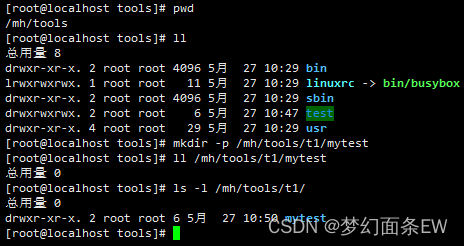
【busybox记录】【shell指令】mkdir
目录 内容来源: 【GUN】【mkdir】指令介绍 【busybox】【mkdir】指令介绍 【linux】【mkdir】指令介绍 使用示例: 创建文件夹 - 默认 创建文件夹 - 创建的同时指定文件权限 创建文件夹 - 指定多级文件路径,如果路径不存在,…...

SQL刷题笔记day6-1
1从不订购的客户 分析:从不订购,就是购买订单没有记录,not in 我的代码: select c.name as Customers from Customers c where c.id not in (select o.customerId from Orders o) 2 部门工资最高的员工 分析:每个部…...

KITTI数据中pose含义
Folder ‘poses’: The folder ‘poses’ contains the ground truth poses (trajectory) for the first 11 sequences. This information can be used for training/tuning your method. Each file xx.txt contains a N x 12 table, where N is the number of frames of this …...
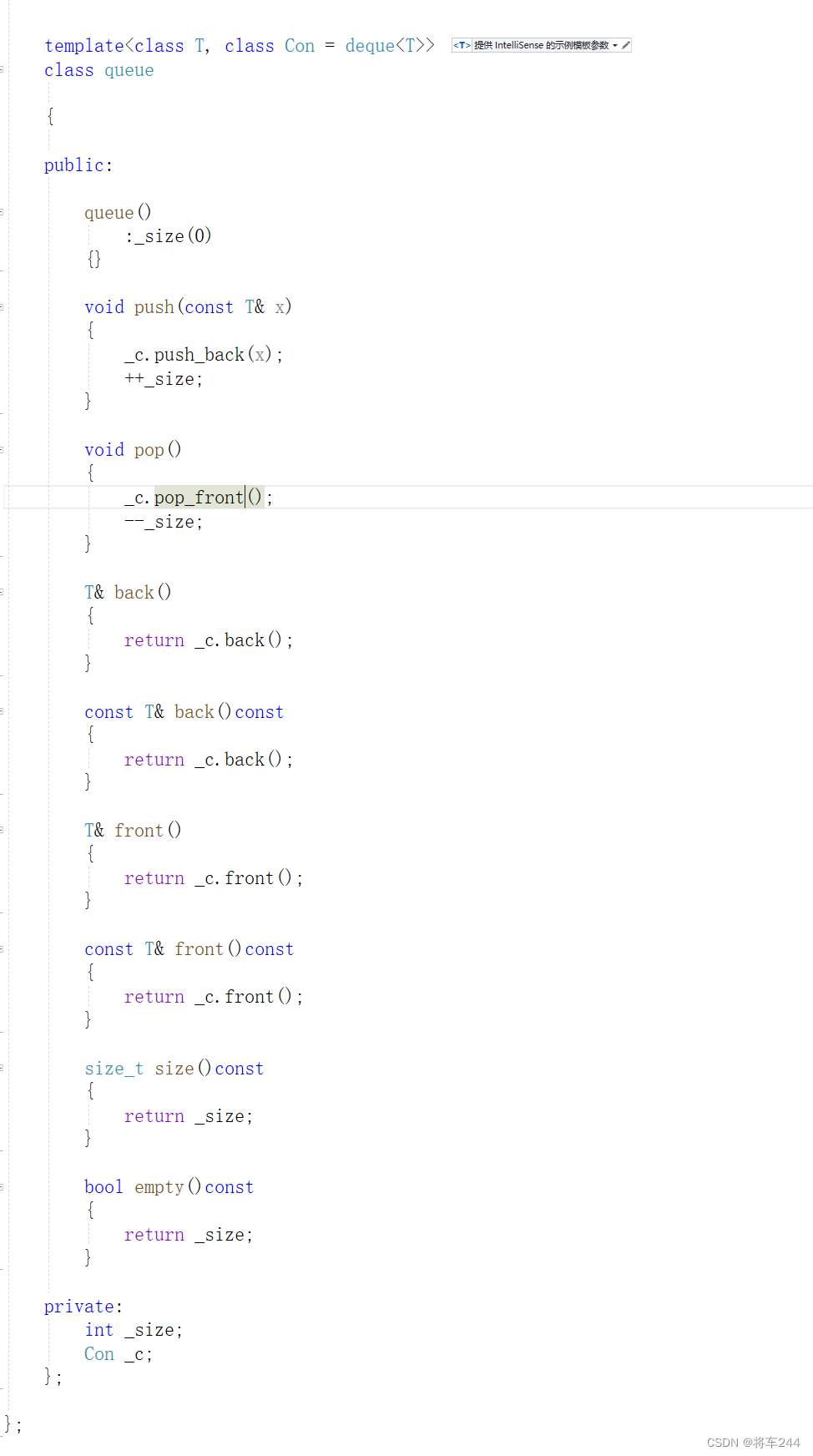
C++模拟实现stack和queue
1 stack 1.1概念 stl栈 1.2栈概念 1.3代码 2 queue 2.1概念 stl队列 2.2队列概念 2.3代码...

awtk踩坑记录一:awtk-web build.py编译过程笔记
工作需求,接触了awtk, 要求把界面部署到web上,期间因为各种编译问题卡的半死,提了不少issue, 经过几天补课,把项目的编译结构给摸了一遍,做个记录,也希望能帮到有同样问题的朋友。 之前python只是略接触过…...

docker容器中解决中文乱码
1. 找到dockerfile文件 2. 编辑Dockerfile 添加 ENV LANG en_US.UTF-8 ENV LANGUAGE en_US:en ENV LC_ALL en_US.UTF-8 3. 生成新的镜像文件 FROM java17_yinpeng:latest MAINTAINER YP <2064676101QQ.COM> ADD jiquan_online_chat.jar jiquan_online_chat #CM…...
)
Javascript 位运算符(,|,^,<<,>>,>>>)
文章目录 一、什么是位运算?二、如何使用1. 位与(AND):&用途(1)数据清零(2)判断奇偶 2. 位或(OR):|用途(1)向下取整 3…...
Golang项目代码组织架构实践
Golang在项目结构上没有强制性规范,虽然这给了开发者很大的自由度,但也需要自己沉淀一套可行的架构。本文介绍了一种项目布局,可以以此为参考设计适合自己的 Golang 项目组织模式。原文: Golang Project Layout Go 有很多强制的或是约定俗成的…...

网工内推 | 国企信息安全工程师,CISP认证优先
01 浙江省公众信息产业有限公司 🔷招聘岗位:安全运营工程师 🔷职责描述: 1. 负责公司内部安全运营平台及其子系统的安全事件管理、事件发现分析、应急响应和系统维护等; 2. 负责风险和漏洞管理,包括漏洞预…...
RAG 高级应用:基于 Nougat、HTML 转换与 GPT-4o 解析复杂 PDF 内嵌表格
一、前言 RAG(检索增强生成)应用最具挑战性的方面之一是如何处理复杂文档的内容,例如 PDF 文档中的图像和表格,因为这些内容不像传统文本那样容易解析和检索。前面我们有介绍过如何使用 LlamaIndex 提供的 LlamaParse 技术解析复…...

《TCP/IP网络编程》(第十二章)I/O复用(2)
下面是基于I/O复用的回声服务器端和客户端代码 1.Linux系统 服务器端代码 #include <stdio.h> #include <stdlib.h> #include <string.h> #include <unistd.h> // POSIX标准定义的通用函数,如close() #include <arpa/inet.h> //…...

AI企业需要“联盟营销”?一文带你探索AI企业营销新玩法!
为什么联盟营销对AI业务有较大优势 联盟营销在电商领域、saas领域与其他产品领域同样有效。在AI业务中,它有效的原因与其他领域大不相同。 高好奇心和试用率 AI领域是创新的热点。它吸引了一群渴望探索和尝试每一项新技术的人群。这种蓬勃的好奇心为聪明的AI企业提…...

你真的会使用Vue3的onMounted钩子函数吗?Vue3中onMounted的用法详解
目录 一、onMounted的前世今生 1.1、onMounted是什么 1.2、onMounted在vue2中的前身 1.2.1、vue2中的onMounted 1.2.2、Vue2与Vue3的onMounted对比 1.3、vue3中onMounted的用法 1.3.1、基础用法 1.3.2、顺序执行异步操作 1.3.3、并行执行多个异步操作 1.3.4、执行一次…...

JavaWeb基础(一)-IO操作
Java I/O工作机制: 注:简要笔记,示例代码可能较少,甚至没有。 1、Java 的 I/O 类库的基本架构。 Java 的 I/O 操作类在包 java.io 下,大概有将近80个类,这些类大概可以分为如下四组。 基于字节操作的…...

拼多多(PDD)社招一面原题
未成年游戏退费 5 月 28 日,中国互联网协会发布《未成年人网络游戏服务消费管理要求(征求意见稿)》团体标准。 该标准是游戏行业首个完整的消费管理规范,可用于未成年人游戏消费退费纠纷解决,也可为相关行政部门、司法…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...
