数据结构基础篇(4)
十六.循环链表
- 概念
- 循环链表是一种头尾相接的链表(最后一个结点的指针域指向头结点,整个链表形成一个环)
- 优点
- 从表任一结点出发均可找到表中其他结点
- 判断终止
- 由于循环链表中没有NULL指针,所以涉及遍历操作时,终止条件不像非循环链表那样判断p或p->next是否为空,而是是否等于头指针
- 循环条件从p!=NULL到p!=L,p->next!=NULL到p->next!=L(单循环链表)
- 时间复杂度
- 头指针表示单循环链表
- 找a~1的时间复杂度:O(1)
- 找a~n的时间复杂度:O(n)
- 注意
- 表的操作常常在表的首尾位置上进行
- 注意
- 尾指针表示单循环链表
- a~1的存储位置是:R->next->next
- a~n的存储位置是:R
- 时间复杂度均为O(1)
- 头指针表示单循环链表
-
LinkList Connect(LinkList Ta,LinkList Tb) //假设Ta.Tb都是非空的单循环链表 {vp=Ta->next; //p存表头结点Ta->next=Tb->next->next; //Tb表头连接Ta表尾delete Tb->next; //释放Tb表头结点Tb->next=p; //修改指针return Tb; }
十七.双向链表
- 双向链表的由来
- 查找某结点的后续结点的执行时间=O(1)
- 单链表结点->有指示后继的指针域->后继结点
- 查找某结点的前驱结点的执行时间=O(n)
- - ->无指示前驱的指针域->依次寻找前驱结点
- 查找某结点的后续结点的执行时间=O(1)
- 双向链表的概念
- 在单链表的每个结点里再增加一个指向其直接前驱的指针域prior,这样链表就形成了有两个方向不同的链。
- 双向链表的特点
- 双向链表也有循环表
- 让头结点的前驱指针指向链表的最后一个节点
- 让最后一个节点的后继指针指向头结点
- 双向链表也有循环表
- 双向链表结构的对称性
- p->prior->next=p=p->next->prior
- 在双向链表中有些操作(如:ListLength、GetElem等),因仅涉及一个方向的指针,所以它们的算法与线性链表的相同。
- 在插入、删除时,则需同事修改两个方向上的指针,两个的操作的时间复杂度都为O(n)。
双向链表的插入
void ListInsert_DuL(DuLinkList &L,Init i,ElemType e) //在带头结点的双向循环链表L中第i个位置之前插入元素e
{if(!(p=GetElemP_DuL(L,i)))return ERROR;s=new DuLNOde;s->date=e;s->prior=p->prior;p->prior->next=s;s->next=p;p->prior=s;return OK;
}//ListInsert_Dul双向链表的删除
void ListDelete_DuL(DuLinkList &L,Init i,ElemType &e) //删除带头节点的双向循环链表L的第i个元素,并返回e
{if(!(p=GetElemP_DuL(L,i)))return ERROR;e=p->data;p->prior->next=p->next;p->next->prio=p->prior;free(p)return OK;
}//ListDelete_Dul十八.单链表,循环链表和双向链表的时间效率比较
| 时间效率的比较 | 查找表头结点(首元结点) | 查找表尾结点 | 查找结点*P的前驱结点 |
| 带头结点的单链表L | L->next 时间复杂度O(1) | 从L->next依次向后遍历时间复杂度O(n) | 通过p->next无法找到其前驱 |
| 带头结点仅设头指针L的循环单链表 | L->next 时间复杂度O(1) | 从L->next依次向后遍历时间复杂度O(n) | 通过p->next可以找到其前驱 时间复杂度O(n) |
| 带头结点仅设尾指针R的循环单链表 | R->next| 时间复杂度O(1) | R 时间复杂度O(1) | 通过p->next可以找到其前驱 时间复杂度O(n) |
| 带头结点的双向循环链表L | L->next 时间复杂度O(1) | L->prior 时间复杂度O(1) | p->prior 时间复杂度O(1) |
十九.顺序表和链表的比较
- 链式存储结构的优点
- 节点空间可以动态申请和释放
- 数据元素的逻辑次序靠节点的指针来指示,插入和删除时不需要移动数据元素
- 链式存储结构的缺点
- 存储密度小,每个结点的指针域需额外占用存储空间。当每个节点的数据域所占字节不多时,指针域所占存储空间的比重闲得很大。
- 存储密度
- 概念
- 结点数据本身所占的存储量和整个节点结构所占的存储量之比
- 公式
- 存储密度=结点数据本身占用的空间/结点占用的空间总量
- 比较
- 顺序表存储密度1,链式小于1。
- 概念
- 存储密度
- 链式存储结构是非随机存储结构。对任一结点的操作都要从头指针依指针链查找到该结点,增加了算法的复杂度。
- 存储密度小,每个结点的指针域需额外占用存储空间。当每个节点的数据域所占字节不多时,指针域所占存储空间的比重闲得很大。
- 顺序表和链表比较图
| 比较项目\存储结构 | 顺序表 | 链表 |
| 空间-存储空间 | 预先分配,导致空间闲置或溢出现象 | 动态分配,不会出现存储空间闲置或溢出现象 |
| 空间-存储密度 | 不用为表示结点间的逻辑关系而增加额外的存储开销,存储密度等于1 | 需要借助指针来体现元素间的逻辑关系,存储密度小于1. |
| 时间-存取元素 | 随机存储,按位置访问元素的时间复杂度O(1) | 顺序存储,按位置访问元素时间复杂度O(n) |
| 时间-插入、删除 | 平均移动约表中一半元素,时间复杂度O(n) | 不需要移动元素,确定插入,删除位置后,时间复杂度O |
| 适用情况 |
|
|
二十.线性表的应用
- 线性表的合并
- 问题
- 假设利用两个线性表La和Lb分别表示两个集合A和B,现要求一个新的集合A=AUB
- 解决
- 问题
void union(List &La,List Lb)
{La_len=ListLength(La);Lb_len=ListLength(Lb);for(i=1;i<=Lb_len;i++){GetElem(Lb,i,e);if(!LocateElem(La,e))ListInsert(&La,++La_len,e); }
} //算法的时间复杂度是:O(ListLength(La)*ListLength(Lb))- 有序表的合并
- 问题
- 已知线性表La和Lb中的数据元素按值非递减有序排列,现要求LA和Lb归并为一个新的线性表Lc,Lc中的数据元素扔按值非递减有序排列。
- 解决
- 创建一个空表Lc
- 依次从La或Lb中“摘取”元素值较小的节点插入到Lc表的最后,直到其中一个表边空为止
- 继续将La或Lb其中一个表的剩余节点插入在Lc表的最后
- 问题
用顺序表来实现
void MergeList_Sq(SqList LA,SqList Lb,SqList &LC)
{pa=LA.elem;pb=LB.elem; //指针pa和pb的初值分别指向两个表的第一个元素LC.length=LA.length+LB.length; //新表长度为待合并量表的长度之和LC.elem=new ElemType[LC.length]; //为合并后的新表分配一个数组空间pc=LC.elem; //指针pc指向新表的第一个元素pa_last=LA.elem+LA.length-1; //指针pa_last指向LA表的最后一个元素pb_last=LB.elem+LB.length-1; //指针pa_last指向LB表的最后一个元素while(pa<=pa_last && pb<=pb_last) //两个表都非空{if(*pa<=*pb)*pc++=*pa++; //依次“摘取”两表中的最小值else *pc++=*pb++; }while(pa<=pa_last)*pc++=*pa++; //LB表已到达表尾,将LA中剩余元素加入LCwhile(pb<=pb_last)*pc=++=*pb++; //LA表已到达表尾,将LB中剩余元素加入LC
} //MergeList_Sq//算法的时间复杂度是:O(ListLength(La)*ListLength(Lb))用链表来实现
void MergeList_L(SqList &La,SqList &Lb,SqList &Lc)
{pa=La->next;pb=Lb->next;pc=Lc=La; //用La的头结点作为Lc的头结点while(pa&&pb){if(pa->data<=pb->data){pc->next=pa;pc=pa;pa=pa->next; } else{pc->next=pb;pc=pb;pb=pb->next; } }pc->next=pa?pa:pb; //插入剩余段delete Lb; //释放Lb的头结点
} //算法的时间复杂度是:O(ListLength(La)*ListLength(Lb))- 一元多项式的运算
- 多项式创建
- 创建一个只有头结点的空链表
- 根据多项式的项的个数n,循环n次执行以下操作
- 生成一个新结点*s
- 输入多项式当前项的系数和指数赋给新节点*s的数据域
- 设置一前驱指针pre,用于指向待找到的第一个大于输入项指数的结点的前驱,pre初值指向头结点。
- 指针q初始化,指向首元结点
- 循链向下逐个比较链表中当前结点与输入项指数,找到第一个大与输入项指数的节点*q
- 将输入项结点*s插入到结点*q之前
void CreatePolyn(Polynomial &P,int n) //输入m项的系数和指数,建立表示多项式的有序链表P
{P=new PNode;p->next=NULL; //先建立一个带头结点的单链表for(i=1;i<=n;i++) //依次输入n个非零项{s=new PNode; //生成新节点cin>>s->coef>>s->expn; //输入系数和指数pre=P; //pre用于保存q的前驱,初值为头结点q=P->next; //q初始化,指向首元结点while(q&&q->expn<s->expn) //找到第一个大于输入项指数的项*q{pre=q;q=q->next; } s->next=q; //将输入项s插入到q和其前驱结点pre之间pre->next=s;}
}相关文章:
)
数据结构基础篇(4)
十六.循环链表 概念 循环链表是一种头尾相接的链表(最后一个结点的指针域指向头结点,整个链表形成一个环)优点 从表任一结点出发均可找到表中其他结点判断终止 由于循环链表中没有NULL指针,所以涉及遍历操作时,终止条…...
使用cad绘制一个螺旋输送机
1、第一步,绘制一个矩形 2、使用绘图中的样条线拟合曲线,绘制螺旋线。 绘制时使用上下辅助线、阵列工具绘制多个竖线保证样条线顶点在同一高度。 3、调整矩形右侧的两个顶点,使其变形。 矩形1和矩形2连接时,使用blend命令&#…...

迭代器模式(行为型)
目录 一、前言 二、迭代器模式 三、总结 一、前言 迭代器模式(Iterator Pattern)是一种行为型设计模式,提供一种方法顺序访问一个聚合对象中各个元素,而又不暴露该对象的内部表示。总的来说就是分离了集合对象的遍历行为,抽象出…...
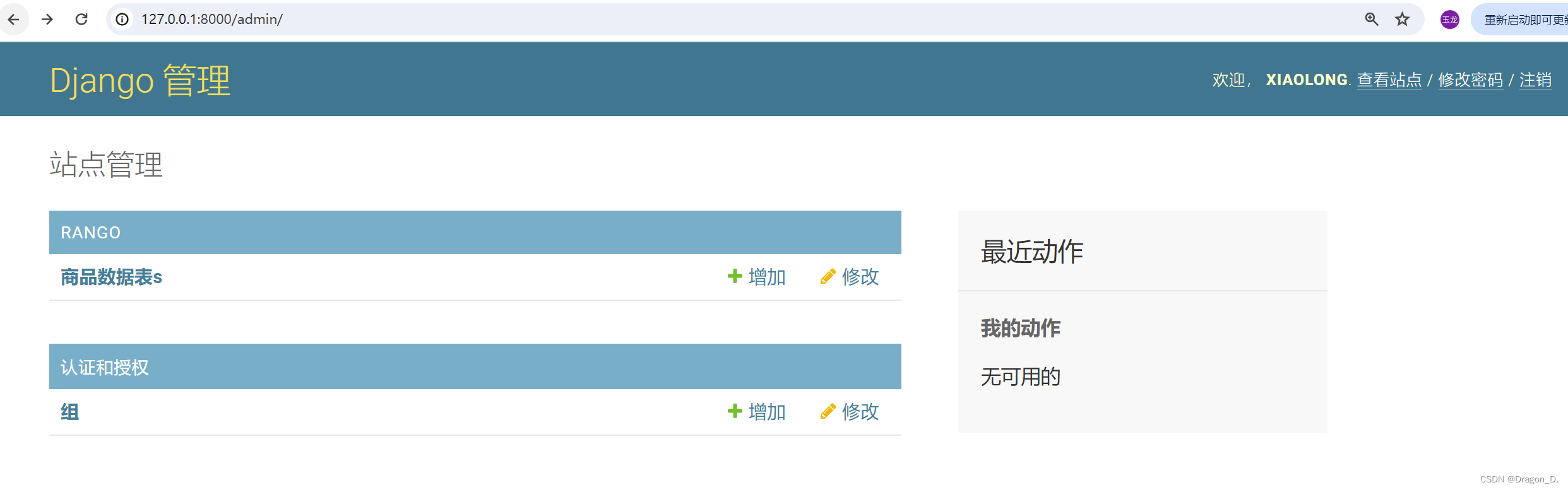
Django——Admin站点(Python)
#前言: 该博客为小编Django基础知识操作博客的最后一篇,主要讲解了关于Admin站点的一些基本操作,小编会继续尽力更新一些优质文章,同时欢迎大家点赞和收藏,也欢迎大家关注等待后续文章。 一、简介: Djan…...

React 组件通信
1.从父组件向子组件传递参数: 父组件可以通过props将数据传递给子组件。子组件通过接收props来获取这些数据。 // 父组件 const ParentComponent () > {const data Hello, Child!;return <ChildComponent childData{data} />; }; // 子组件 const ChildCompone…...
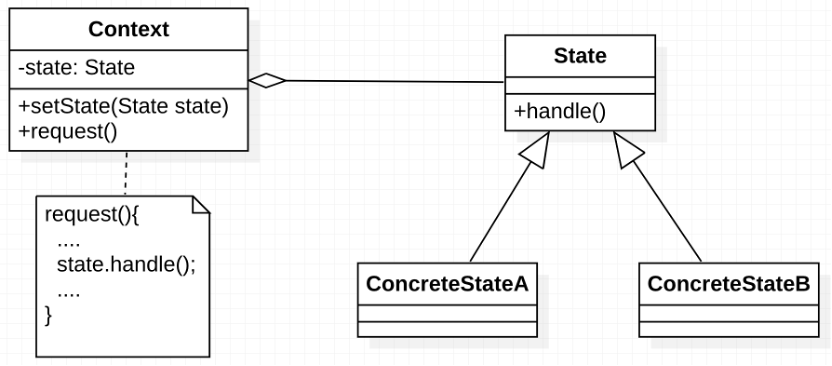
【再探】设计模式—访问者模式、策略模式及状态模式
访问者模式是用于访问复杂数据结构的元素,对不同的元素执行不同的操作。策略模式是对于具有多种实现的算法,在运行过程中可动态选择使用哪种具体的实现。状态模式是用于具有不同状态的对象,状态之间可以转换,且不同状态下对象的行…...

新人硬件工程师,工作中遇到的问题list
新人硬件工程师能够通过面试,已经证明是能够胜任硬件工程师职责,当然胜任的时间会延迟,而不是当下,为什么呢?因为学校学习和公司做产品,两者之间有差异,会需要适应期。今天来看看新人硬件工程师…...

如何在Linux系统中搭建Zookeeper集群
一、概述 ZooKeeper是一个开源的且支持分布式部署的应用程序,是Google的Chubby一个开源的实现;它为分布式应用提供了一致性服务支持,包括:配置维护、域名服务、分布式同步、组服务等。 官网:https://zookeeper.apach…...

C++:vector的模拟实现
hello,各位小伙伴,本篇文章跟大家一起学习《C:vector的模拟实现》,感谢大家对我上一篇的支持,如有什么问题,还请多多指教 ! 如果本篇文章对你有帮助,还请各位点点赞!&…...
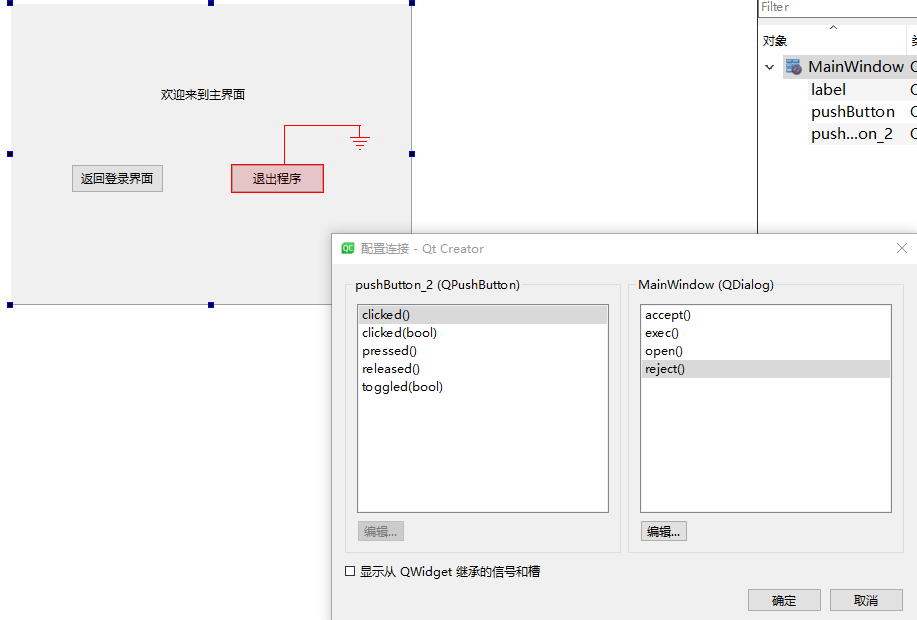
QT系列教程(5) 模态对话框消息传递
模态对话框接受和拒绝消息 我们创建一个模态对话框,调用exec函数后可以根据其返回值进行不同的处理,exec的返回值有两种,Qt的官方文档记录的为 QDialog::Accepted QDialog::RejectedAccepted 表示接受消息, Rejected表示拒绝消息…...
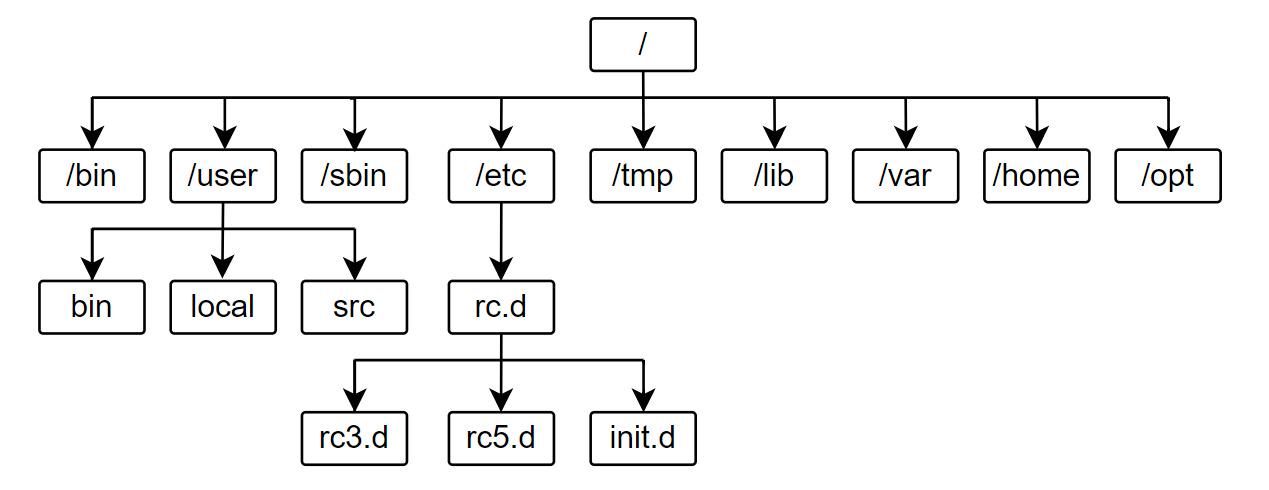
Linux学习笔记(清晰且清爽)
本文首次发布于个人博客 想要获得最佳的阅读体验(无广告且清爽),请访问本篇笔记 Linux安装 关于安装这里就不过多介绍了,安装版本是CentOS 7,详情安装步骤见下述博客在VMware中安装CentOS7(超详细的图文教…...
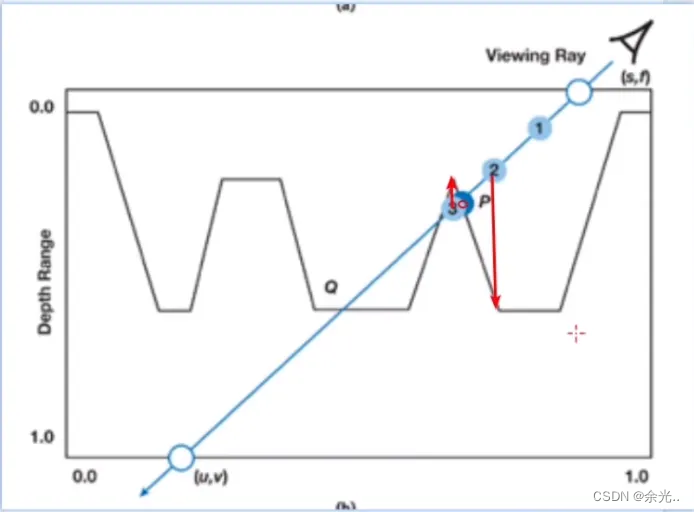
2.5Bump Mapping 凹凸映射
一、Bump Mapping 介绍 我们想要在屏幕上绘制物体的细节,从尺度上讲,一个物体的细节分为:宏观、中观、微观宏观尺度中其特征会覆盖多个像素,中观尺度只覆盖几个像素,微观尺度的特征就会小于一个像素宏观尺度是由顶点或…...

数字化前沿:Web3如何引领未来技术演进
在当今数字化时代,随着技术的不断发展和创新,Web3作为一种新兴的互联网范式,正逐渐成为数字化前沿的代表。Web3以其去中心化、加密安全的特性,正在引领着未来技术的演进,为全球范围内的科技创新带来了新的可能性和机遇…...
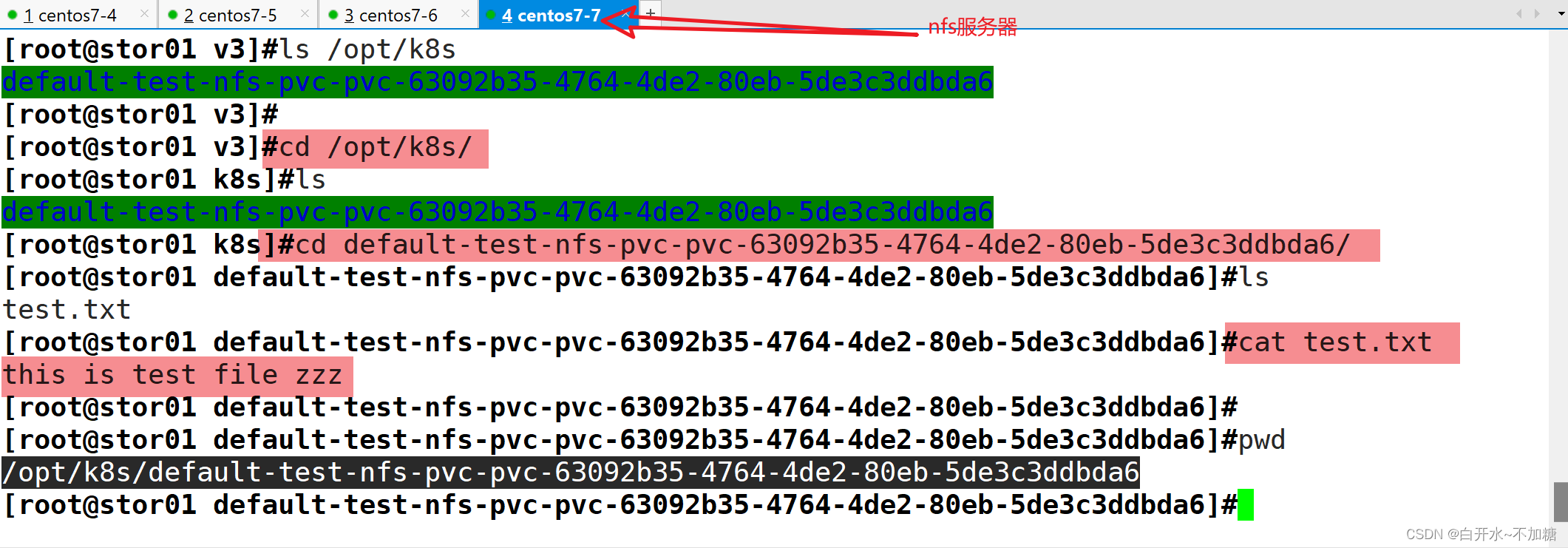
【kubernetes】探索k8s集群的存储卷、pvc和pv
目录 一、emptyDir存储卷 1.1 特点 1.2 用途 1.3部署 二、hostPath存储卷 2.1部署 2.1.1在 node01 节点上创建挂载目录 2.1.2在 node02 节点上创建挂载目录 2.1.3创建 Pod 资源 2.1.4访问测试 2.2 特点 2.3 用途 三、nfs共享存储卷 3.1特点 3.2用途 3.3部署 …...
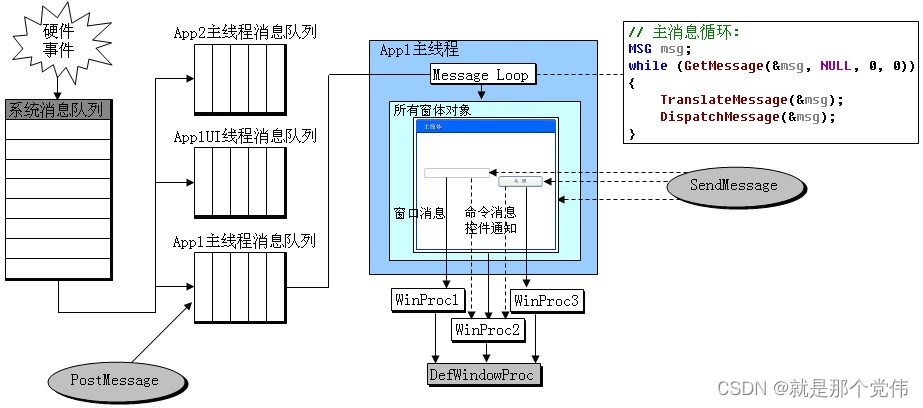
UI线程和工作线程
引用:windows程序员面试指南 工作线程 只处理逻辑的线程,例如:启动一个线程,用来做一个复杂的计算,计算完成之后,此线程就自动退出,这种线程称为工作线程 UI线程 Windows应用程序一般由窗口…...

RandLA-Net 训练自定义数据集
https://arxiv.org/abs/1911.11236 搭建训练环境 git clone https://github.com/QingyongHu/RandLA-Net.git搭建 python 环境 , 这里我用的 3.9conda create -n randlanet python3.9 source activate randlanet pip install tensorflow2.15.0 -i https://pypi.tuna.tsinghua.e…...

洛谷 B3642:二叉树的遍历 ← 结构体方法 链式前向星方法
【题目来源】https://www.luogu.com.cn/problem/B3642【题目描述】 有一个 n(n≤10^6) 个结点的二叉树。给出每个结点的两个子结点编号(均不超过 n),建立一棵二叉树(根结点的编号为 1),如果是叶子结点&…...

飞腾+FPGA多U多串全国产工控主机
飞腾多U多串工控主机基于国产化飞腾高性能8核D2000处理器平台的国产自主可控解决方案,搭载国产化固件,支持UOS、银河麒麟等国产操作系统,满足金融系统安全运算需求,实现从硬件、操作系统到应用的完全国产、自主、可控,是国产金融信…...

uni-app实现页面通信EventChannel
uni-app实现页面通信EventChannel 之前使用了EventBus的方法实现不同页面组件之间的一个通信,在uni-app中,我们也可以使用uni-app API —— uni.navigateTo来实现页面间的通信。注:2.8.9 支持页面间事件通信通道。 1. 向被打开页面传送数据…...

等保系列之——网络安全等级保护测评工作流程及工作内容
#等保测评##网络安全# 一、网络安全等级保护测评过程概述 网络安全等级保护测评工作过程包括四个基本测评活动:测评准备活动、方案编制活动、现场测评活动、报告编制活动。而测评相关方之间的沟通与洽谈应贯穿整个测评过程。每一项活动有一定的工作任务。如下表。…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...
