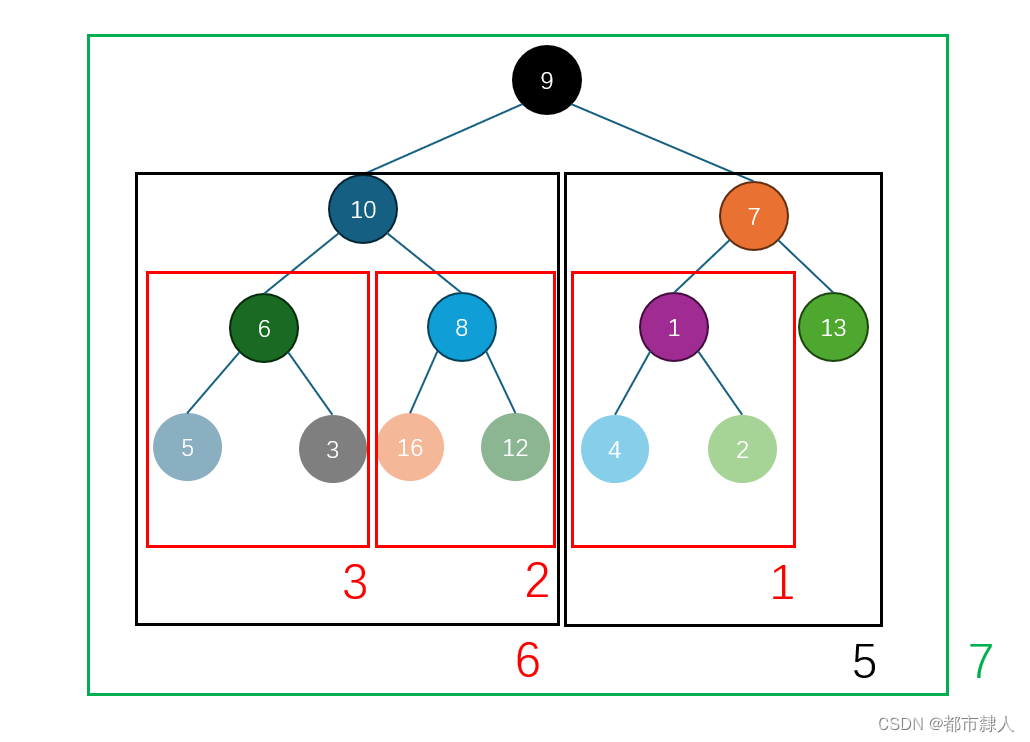
堆排序详细理解
目录
一、前备知识
二、建堆
2.2.1 向上调整算法建堆
2.2.2 向下调整算法建堆
三、排序
3.1 常见问题
3.2 思路
3.3 源码
一、前备知识
详细图解请点击:二叉树的顺序实现-堆-CSDN博客
本文只附上向上/向下调整算法的源码
//交换
void Swap(int* p, int* q)
{int tmp = *p;*p = *q;*q = tmp;
}
//向下调整算法
void AdjustDown(int* a, int n, int parent)
{//左孩子的下标int child = parent * 2 + 1;while (child<n){//找到两个孩子中较小的孩子-假设法if (child + 1 < n && a[child + 1] < a[child]){child++;}if (a[parent] > a[child]){Swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;}else{break;}}
}
//向上调整算法
void AdjustUp(int* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] > a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}二、建堆
堆排序堆排序,先有堆才能排序,所以排序的第一步是要将一个一般的数组建成堆。
注:由于建大堆还是小堆仅仅取决于自定的大小于号,本文下述建堆都以小堆为例
2.2.1 向上调整算法建堆
思路:
- 单一的一个结点可以看成一个堆
- 后续的所有结点都可以看作是插入结点
所以只需要循环插入所有后续结点即可
void BuildHeap1(int* a, int n)
{//把根节点看作是堆,剩下的结点看作插入结点,开始依次插入for (int i = 1; i < n; i++){AdjustUp(a, i);}
}2.2.2 向下调整算法建堆
错误思路:
向下调整算法要求左右子树必须为大/小堆,所以从根节点开始结点开始建堆的做法是错误的
正确思路:
上文说:单一的一个结点可以看成一个堆。所以从最后一个叶子节点的父节点开始向下调整,不断循环所有父节点,就可以保证他的左右子树都是堆。
void BuildHeap2(int* a, int n)
{//从最后一个叶子结点的父结点开始调for (int i = ((n - 1) - 1) / 2; i >= 0; i--){AdjustDown(a, n, i);}
}三、排序
3.1 常见问题
- 为什么建堆后依然还要排序?
大堆/小堆的定义注定了堆仅仅能保证父节点大于孩子结点,无法保证孩子结点按照大于/小于的次序严格排列!!!
- 升序建小堆,降序建大堆的思路是否可行?
- 升序建小堆:首先对 n 个数建小堆,选出最小的数,接着对剩下的 n-1 个数建小堆,选出第二小的数,不断重复上述过程。若用向上调整算法可行但时间复杂度太高,若使用向下调整算法时,对n-1个调整就会发现:原先的孩子父亲关系全乱,不可行。
- 降序建大堆:首先对 n 个数建小堆,选出最小的数,接着对剩下的 n-1 个数建大堆,选出第二大的数,不断重复上述过程。使用向下调整算法时,对n-1个调整就会发现:原先的孩子父亲关系全乱,不可行。
3.2 思路
- 本质上是堆删除的思路。利用堆的特性,无论是大堆还是小堆,根节点的值一定是最大/小的数。这样每进行一次调整,就会选择出最小/大,次小/大......便可以实现排序。
- 为了防止出现父子关系乱序的问题,将每次找到的最值放在堆的末位置,对前n-1个元素进行向下调整,便可以完美解决排序问题
- 由此可以总结:升序建大堆,降序建小堆。
由此,我们可以归纳出堆排序算法的步骤:
1. 把无序数组构建成二叉堆。
2. 循环删除堆顶元素,移到数组尾部,调节堆产生新的堆顶。
3.3 源码
//降序建小堆
void HeapSortDown(int* a, int n)
{//建小堆for (int i = ((n - 1) - 1) / 2; i >= 0; i--){AdjustDown(a, n, i);}//排序int end = n - 1; //定位数组最后一个位置while (end > 0){Swap(&a[0], &a[end]); // 将堆顶元素和堆中最后一个元素交换,把最大的数(堆顶)放到最后AdjustDown(a, end, 0);end--; // 调整前n-1个元素}
}
相关文章:

堆排序详细理解
目录 一、前备知识 二、建堆 2.2.1 向上调整算法建堆 2.2.2 向下调整算法建堆 三、排序 3.1 常见问题 3.2 思路 3.3 源码 一、前备知识 详细图解请点击:二叉树的顺序实现-堆-CSDN博客 本文只附上向上/向下调整算法的源码 //交换 void Swap(int* p, int* …...

RK3588+FPGA+AI高性能边缘计算盒子,应用于视频分析、图像视觉等
搭载RK3588(四核 A76四核 A55),CPU主频高达 2.4GHz ,提供1MB L2 Cache 和 3MB L3 ,Cache提供更强的 CPU运算能力,具备6T AI算力,可扩展至38T算力。 产品规格 系统主控CPURK3588,四核…...

07-操作元素(键盘和鼠标事件)
在前面的文章中重点介绍了一些元素的定位方法,定位到元素后,就需要操作元素了。本篇总结了web页面常用的一些操作元素方法,可以统称为行为事件。 一、简单操作 点击按钮(鼠标左键):click()清空输入框&…...

3389,为了保障3389端口的安全,我们可以采取的措施
3389端口,作为远程桌面协议(RDP)的默认端口,广泛应用于Windows操作系统中,以实现远程管理和控制功能。然而,正因为其广泛使用,3389端口也成为许多潜在安全威胁的入口。因此,确保3389…...

Java集合【超详细】2 -- Map、可变参数、Collections类
文章目录 一、Map集合1.1 Map集合概述和特点【理解】1.2 Map集合的基本功能【应用】1.3 Map集合的获取功能【应用】1.4 Map集合的两种遍历方式 二、HashMap集合2.1 HashMap集合概述和特点【理解】2.2 HashMap的组成、构造函数2.3 put、查找方法2.4 HashMap集合应用案例【应用】…...
最佳 Mac 数据恢复:恢复 Mac 上已删除的文件
尝试过许多 Mac 数据恢复工具,但发现没有一款能达到宣传的效果?我们重点介绍最好的 Mac 数据恢复软件 没有 Mac 用户愿意担心数据丢失,但您永远不知道什么时候会发生这种情况。无论是意外删除 Mac 上的重要文件、不小心弄湿了 Mac、感染病毒…...
芋道系统,springboot+vue3+mysql实现地址的存储与显示
1.效果图 2.前端实现: <el-form-item label"地址" prop"entrepriseAddress"><el-cascaderv-model"formData.entrepriseAddress"size"large":options"region"/></el-form-item> //导入组件 im…...

【C++】C++11新特性:列表初始化、声明、新容器、右值引用、万能引用和完美转发
目录 一、列表初始化 1.1 { } 初始化 1.2 std::initializer_list 二、声明 2.1 auto 2.2 decltype 2.3 nullptr 三、新容器 四、右值引用和移动语义 4.1 左值和左值引用 4.2 右值和右值引用 4.3 左值引用与右值引用比较 4.4 右值引用使用场景和意义:移…...
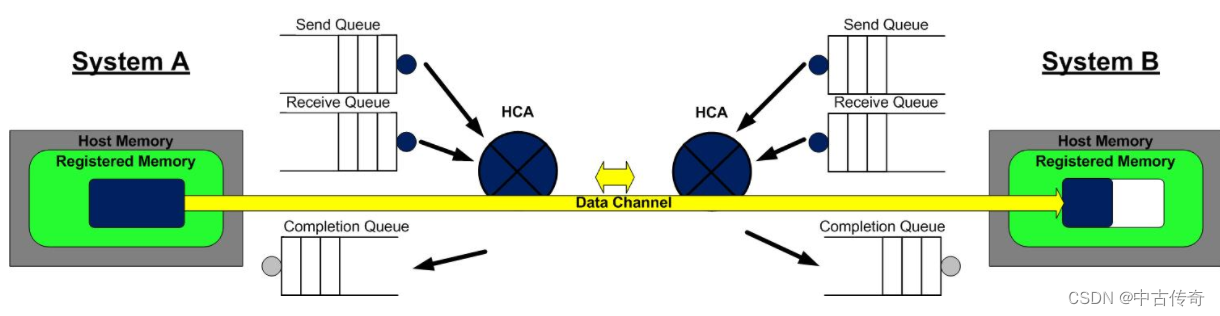
【IB Protocal Serial--WQE】
IB Protocal Serial--WQE 1 Intro1.1 What1.2 IBA WQE 本系列文章介绍RDMA技术的具体实现–InfiniBand Protocal; Introduce the features, capalities,components, and elements of IBA. the principles of operation. 1 Intro 1.1 What 理解IB协议下面这三句话对…...

C++ 混合运算的类型转换
一 混合运算和隐式转换 257 整型2 浮点5 行吗?成吗?中不中? C 中允许相关的数据类型进行混合运算。 相关类型。 尽管在程序中的数据类型不同,但逻辑上进行这种运算是合理的相关类型在混合运算时会自动进行类型转换,再…...

线性时间选择
给定线性序集中n个元素和一个整数k,1≤k≤n,要求找出这n个元素中第k小的元素 #include<iostream> #include<cstdlib> #include<time.h> using namespace std; int a[100]; int Random(int left,int right) {srand(time(NULL));return …...

【对算法期中卷子的解析和反思】
一、程序阅读并回答问题(共30分) #include<cstdio>#include<cstring>#include<iostream>using namespace std;char chess[10][10];int sign[10];int n, k, ans;void dfs(int x, int k) { if (k 0){ans;return; } if (xk-1 >…...

sudo apt update sudo: apt: command not found
CentOS或RHEL(Red Hat Enterprise Linux)系统上,包管理器是yum或dnf,而不是apt。您可以使用yum或dnf来安装软件包。以下是如何在CentOS或RHEL上安装Git的详细步骤: 1. 使用yum安装Git 首先,更新软件包列表&…...
ios:文本框默认的copy、past改成中文复制粘贴
问题 ios 开发,对于输入框的一些默认文案展示,如复制粘贴是英文的,那么如何改为中文的呢 解决 按照路径找到这个文件 ios/项目/Info.plist,增加 <key>CFBundleAllowMixedLocalizations</key> <true/> <…...
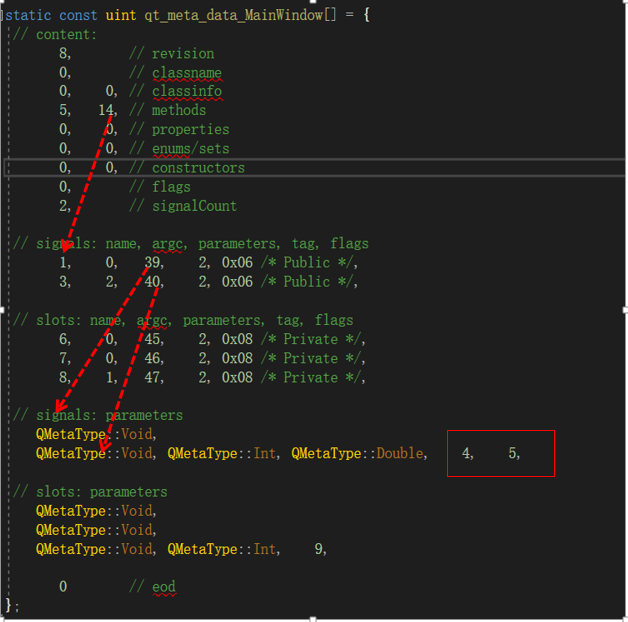
Qt moc系统的黑魔法?
Qt的元对象系统(Meta-Object System)是Qt框架的核心功能之一,为C语言增加了一些动态特性,借助元对象系统Qt可以实现以下功能 信号与槽机制(Signals and Slots)运行时类型信息(Run-Time Type In…...

MyBatis开发中常用总结
文章目录 常用MyBatis参数映射单个参数多个参数使用索引【不推荐】Param注解Map传参POJO【推荐】List数组 动态标签\<if>标签\<trim>标签\<where>标签\<set>标签\<foreach>标签 MyBatis查询一对一一对多 常用MyBatis参数映射 单个参数 XML中可…...

Git基本使用教程(学习记录)
参考文章链接: Git教程(超详细,一文秒懂) RUNOOB Git教程 Git学习记录 1Git概述 1.1版本控制软件功能 版本管理:更新或回退到历史上任何版本,数据备份共享代码:团队间共享代码,…...
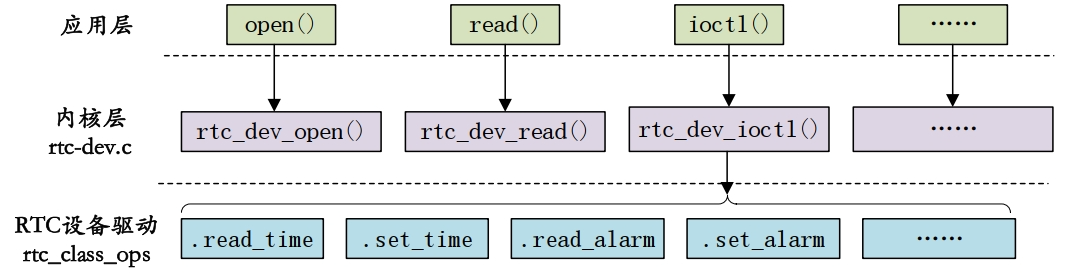
【Linux-RTC】
Linux-RTC ■ rtc_device 结构体■ RTC 时间查看与设置■ 1、时间 RTC 查看■ 2、设置 RTC 时间 ■ rtc_device 结构体 Linux 内核将 RTC 设备抽象为 rtc_device 结构体 rtc_device 结构体,此结构体定义在 include/linux/rtc.h 文件中 ■ RTC 时间查看与设置 ■ 1…...

机器学习目录
文章目录 基本概念有监督学习回归问题分类问题 无监督学习聚类问题异常检测 基本概念 pass 有监督学习 回归问题 通过拟合函数,解决连续值的预测问题梯度下降法优化;最小二乘法求解;度量指标 均方误差;均方根误差;平…...

React开发环境配置详细讲解-04
环境简介 前端随着规范化,可以说规范和环境插件配置满天飞,笔者最早接触的是jquery,那个开发非常简单,只要引入jquery就可以了,当时还写了一套UI框架,至今在做小型项目中还在使用,show一张效果…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...