【对算法期中卷子的解析和反思】
一、程序阅读并回答问题(共30分)
- #include<cstdio>
- #include<cstring>
- #include<iostream>
- using namespace std;
- char chess[10][10];
- int sign[10];
- int n, k, ans;
- void dfs(int x, int k)
- {
- if (k == 0){
- ans++;
- return;
- }
- if (x+k-1 > n)
- return;
- for (int i = x; i <= n; i++)
- for (int j = 1; j <= n; j++)
- if (!sign[j] && chess[i][j] == '#'){
- sign[j] = 1;
- dfs(i + 1, k - 1);
- sign[j] = 0;
- }
- }
- int main()
- {
- while (cin >> n >> k){
- memset(chess, 0, sizeof(chess));
- memset(sign, 0, sizeof(sign));
- if (n == -1 || k == -1)
- break;
- for (int i = 1; i <= n; i++)
- for (int j = 1; j <= n; j++)
- cin >> chess[i][j];
- ans = 0;
- dfs(1, k);
- cout << ans << endl;
- }
- return 0;
- }
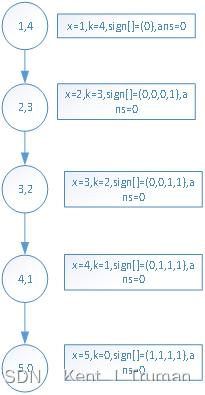
设程序的输入如下,请写出程序执行到35行时变量chess的值。(3分)
4 4
...#
..#.
.#..
#...
-1 -1
这里的坑点就是chess[][]的范围是[0-9][0-9],很多人没考虑多余的部分
chess[1][1]~Chess[1][4]的值分别为“.”,“.”,“.”,“#”。
chess[2][1]~Chess[2][4]的值分别为“.”,“.”,“#”,“.”。
chess[3][1]~Chess[3][4]的值分别为“.”,“#”,“.”,“.”。
chess[4][1]~chess[4][4]的值分别为“#”,“.”,“.”,“.”。
其余值为0。
分析函数dfs(.)的时间复杂度,写出分析求解过程。(12分)
这个时间复杂度也是,跟之前的答案出来的还不一样,逆天
以前这个,纯纯数学公式推出来的,啥初始条件都是浮云

你想想,右边是组合数,我们可以理解为n列中选K列,再粗略的n行选、n-1行选......左边也该是个阶乘来着......无语
现在这个

若采用问题(1)中的输入,分析该程序的求解过程。(15分)
这个跟老师之前出的类似题写的真不一样,服了。
我觉得我这个写的是对的

二、算法分析题 (共40分)
某班级的同学正在玩一个游戏。他们在某个时刻把一个物品摆放到跑道的某个位置,设跑道的长度为10米且是笔直的。游戏前他们会把每个物品的价格,物品出现的时间和位置告诉给玩游戏的同学。假设玩游戏的同学刚开始时站在跑道的某个位置,他每秒跑的距离不超过1米。当然他可以不跑,也可以朝前或者朝后跑。他每跑到一个位置便可以快速的拾取该物品,然后以同样的速度跑到下一个位置。请问,他最多能够获得的物品的总价格是多少?
输入:
输入数据的第一行包含两个正整数n(0<n<100)和m(0<=m<=10),其中n表示待摆放的物品的个数,m表示刚开始时玩游戏同学所在的位置;在接下来的n行中,每行有3个整数x, t(0<T< 100000)和p,表示在第t秒会在x位置上摆放一个价值为p的物品。同一时刻可能在同一位置摆放多个物品。
输出:
玩游戏的同学最多能够拾取的物品的总价格是多少?
样例输入:
4 4
2 1 1
3 2 5
5 3 1
6 2 3
样例输出:
5
要求:
请写出采用穷举法求解该问题的伪代码,并画出样例输入时的解空间树。(10分)
我们的算法的起点都不一样,真不知道这咋整
请写出采用动态规划算法求解上述问题的伪代码,并用样例输入对其进行验证,写出求解过程。(20分)
也是算法不一样
【拾取问题】-CSDN博客

好吧,老师写的比我好,我需要递归,他不用,但是这个有点颠覆我的思维,我没看懂
| 行号 | 执行次数 | i | j | dp[i][j] | mValue |
| 6 | 1 | 0 | 1 | 0 | 0 |
| 6 | 2 | 0 | 2 | 0 | 0 |
| 6 | 3 | 0 | 3 | 0 | 0 |
| 6 | 5 | 1 | 2 | 0 | 0 |
| 4 | 15 | 4 | 3 | 5 | 0 |
| 10 | 1 | - | - | - | 5 |
我也可以给这个表格,但是定义都不一样,咋能指望一模一样
表3 动态规划求解结果(dp[i][j])
| (j,i) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 5 | 0 | 0 | 3 | 0 | 0 | 0 | 0 |
| 3 | 0 | 0 | 5 | 5 | 5 | 4 | 3 | 3 | 0 | 0 | 0 |
分析(1)中算法的时间复杂度,写出分析求解过程。(10分)
没看懂咋分析的
题(1)为三叉树,深度为lTime+1,因此T(0)=3T(1),T(lTime)=O(1),其时间复杂度为O(3lTime)。
三、算法设计及实现(共30分)
有一个2*n大小的矩形地板,用2*2和2*1大小的瓷砖方块来填满它。求一共有多少种不同的放法?如下所示:

输入:
输入包含若干行,每一行包含一个整数n(0<=n<=250),表示矩形地板的长度。
输出:
对于每一行的输出,输出一行整数,表示矩形地板的不同的摆放方法。
样例输入:
2
8
12
100
200
样例输出:
3
171
2731
845100400152152934331135470251
1071292029505993517027974728227441735014801995855195223534251
要求:
当n=2时,画出不同的摆放方法。(5分)
三种,略
假设长度为n时摆放两种砖块的不同摆放方法有f(n)种。如果前面两块摆放2*2的砖块,则剩余的n-2块砖块摆放两种不同砖块的摆放方法有多少种?(5分)
这里竟然是把f[n]当作函数,估计是老师像让我们用动态规划做,所以提示,答案是f[n-2]
假设长度为n时摆放两种砖块的不同摆放方法有f(n)种。如果前面1块摆放2*1的砖块,则剩余的n-1块砖块摆放两种不同的砖块总共有多少种不同的摆放方法?(5分)
f[n-1]
按题目要求编写完整程序,并简要说明算法求解思想。(15分)
【地板拼接问题】-CSDN博客
该算法的求解思想:
假设地板长度为n,有f[n]种放置2*1和2*2砖块的方法。假设某一块放2*2,则有方法数f[n-2];假设某一块竖着放2*1,则有方法数f[n-1];假设某一块横着放2*1,则有方法数f[n-2],因此得出转移方程f[n] = 2 * f[n-2] + f[n-1]
于是将求解dp[n]的问题,转化为求解dp[n-1]和dp[n-2]的问题,从而不断分解为简单的子问题,直到分解为最小子问题dp[0]=1,dp[1]=1。
相关文章:

【对算法期中卷子的解析和反思】
一、程序阅读并回答问题(共30分) #include<cstdio>#include<cstring>#include<iostream>using namespace std;char chess[10][10];int sign[10];int n, k, ans;void dfs(int x, int k) { if (k 0){ans;return; } if (xk-1 >…...

sudo apt update sudo: apt: command not found
CentOS或RHEL(Red Hat Enterprise Linux)系统上,包管理器是yum或dnf,而不是apt。您可以使用yum或dnf来安装软件包。以下是如何在CentOS或RHEL上安装Git的详细步骤: 1. 使用yum安装Git 首先,更新软件包列表&…...
ios:文本框默认的copy、past改成中文复制粘贴
问题 ios 开发,对于输入框的一些默认文案展示,如复制粘贴是英文的,那么如何改为中文的呢 解决 按照路径找到这个文件 ios/项目/Info.plist,增加 <key>CFBundleAllowMixedLocalizations</key> <true/> <…...
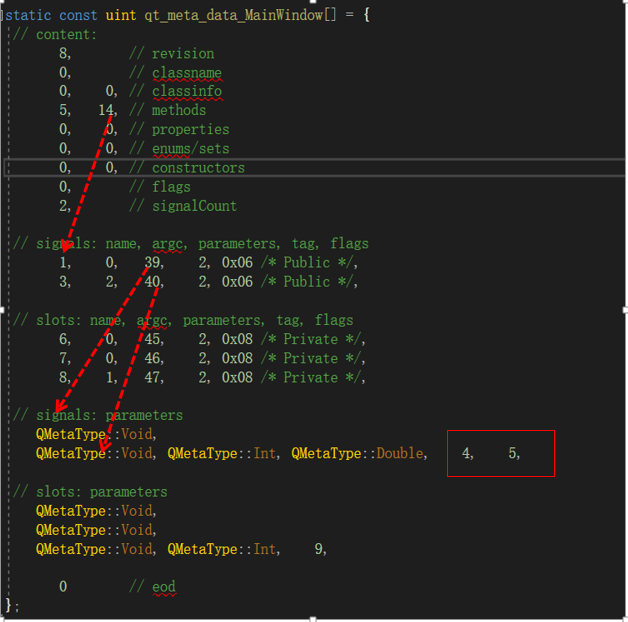
Qt moc系统的黑魔法?
Qt的元对象系统(Meta-Object System)是Qt框架的核心功能之一,为C语言增加了一些动态特性,借助元对象系统Qt可以实现以下功能 信号与槽机制(Signals and Slots)运行时类型信息(Run-Time Type In…...

MyBatis开发中常用总结
文章目录 常用MyBatis参数映射单个参数多个参数使用索引【不推荐】Param注解Map传参POJO【推荐】List数组 动态标签\<if>标签\<trim>标签\<where>标签\<set>标签\<foreach>标签 MyBatis查询一对一一对多 常用MyBatis参数映射 单个参数 XML中可…...

Git基本使用教程(学习记录)
参考文章链接: Git教程(超详细,一文秒懂) RUNOOB Git教程 Git学习记录 1Git概述 1.1版本控制软件功能 版本管理:更新或回退到历史上任何版本,数据备份共享代码:团队间共享代码,…...
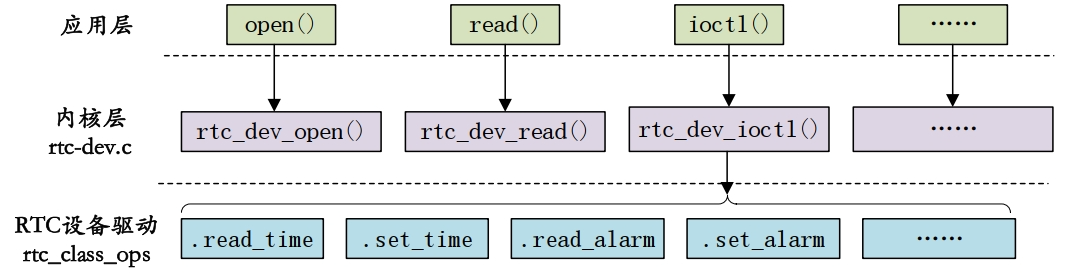
【Linux-RTC】
Linux-RTC ■ rtc_device 结构体■ RTC 时间查看与设置■ 1、时间 RTC 查看■ 2、设置 RTC 时间 ■ rtc_device 结构体 Linux 内核将 RTC 设备抽象为 rtc_device 结构体 rtc_device 结构体,此结构体定义在 include/linux/rtc.h 文件中 ■ RTC 时间查看与设置 ■ 1…...

机器学习目录
文章目录 基本概念有监督学习回归问题分类问题 无监督学习聚类问题异常检测 基本概念 pass 有监督学习 回归问题 通过拟合函数,解决连续值的预测问题梯度下降法优化;最小二乘法求解;度量指标 均方误差;均方根误差;平…...

React开发环境配置详细讲解-04
环境简介 前端随着规范化,可以说规范和环境插件配置满天飞,笔者最早接触的是jquery,那个开发非常简单,只要引入jquery就可以了,当时还写了一套UI框架,至今在做小型项目中还在使用,show一张效果…...

Go 如何通过 Kafka 客户端库 生产与消费消息
文章目录 0.前置说明1. confluent-kafka-go2. sarama3. segmentio/kafka-go4. franz-go选择建议 1.启动 kafka 集群2.安装 confluent-kafka-go 库3.创建生产者特殊文件说明如何查看.log文件内容 4.创建消费者 0.前置说明 Go 语言中有一些流行的 Kafka 客户端库。以下是几个常用…...
【设计模式深度剖析】【B】【结构型】【对比】| 主要区别包装的不同
👈️上一篇:享元模式 回 顾:结构型设计模式 1.代理模式👈️ 2.装饰器模式👈️ 3.适配器模式👈️ 4.组合模式👈️ 5.桥接模式👈️ 6.外观模式👈️ 7.享元模式&#x…...

信息学奥赛初赛天天练-17-阅读理解-浮点数精准输出与海伦公式的巧妙应用
PDF文档公众号回复关键字:20240531 1 2023 CSP-J 阅读程序1 阅读程序(程序输入不超过数组成字符串定义的范围:判断题正确填√,错误填;除特殊说明外,判断题1.5分,选择题3分,共计40分࿰…...

mysql - 为什么MySQL不建议使用NULL作为列默认值?
为什么MySQL不建议使用NULL作为列默认值? InnoDB有4中行格式: Redundant : 非紧凑格式,5.0 版本之前用的行格式,目前很少使用,Compact : 紧凑格式,5.1 版本之后默认行格式,可以存储更多的数据Dynamic , Compressed : 和Compact类似,5.7 版本之后默认使…...

数据分析案例-在线食品订单数据可视化分析与建模分类
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…...

构建LangChain应用程序的示例代码:2、使用LangChain库实现的AutoGPT示例:查找马拉松获胜成绩
AutoGPT 示例:查找马拉松获胜成绩 实现 https://github.com/Significant-Gravitas/Auto-GPT,使用LangChain基础组件(大型语言模型(LLMs)、提示模板(PromptTemplates)、向量存储(VectorStores)、嵌入(Embeddings)、工具(Tools))。…...

代码随想录算法训练营第三十四 |● 1005.K次取反后最大化的数组和 ● 134. 加油站 ● 135. 分发糖果
今天的解析写在了代码注释中 1005.K次取反后最大化的数组和 讲解链接:https://programmercarl.com/1005.K%E6%AC%A1%E5%8F%96%E5%8F%8D%E5%90%8E%E6%9C%80%E5%A4%A7%E5%8C%96%E7%9A%84%E6%95%B0%E7%BB%84%E5%92%8C.html class Solution { public:static bool cmp(i…...

GB-T 43206-2023 信息安全技术 信息系统密码应用测评要求
GB-T 43206-2023 信息安全技术 信息系统密码应用测评要求 编写背景 随着信息技术的飞速发展,信息系统在社会经济活动中扮演着越来越重要的角色。信息安全问题也随之成为社会关注的焦点。GB-T 43206-2023《信息安全技术 信息系统密码应用测评要求》是针对信息系统中…...

线程进阶-1 线程池
一.说一下线程池的执行原理 1.线程池的七大核心参数 (1)int corePoolSize:核心线程数。默认情况下核心线程会一直存活,当设置allowCoreThreadTimeout为true时,核心线程也会被超时回收。 (2)i…...
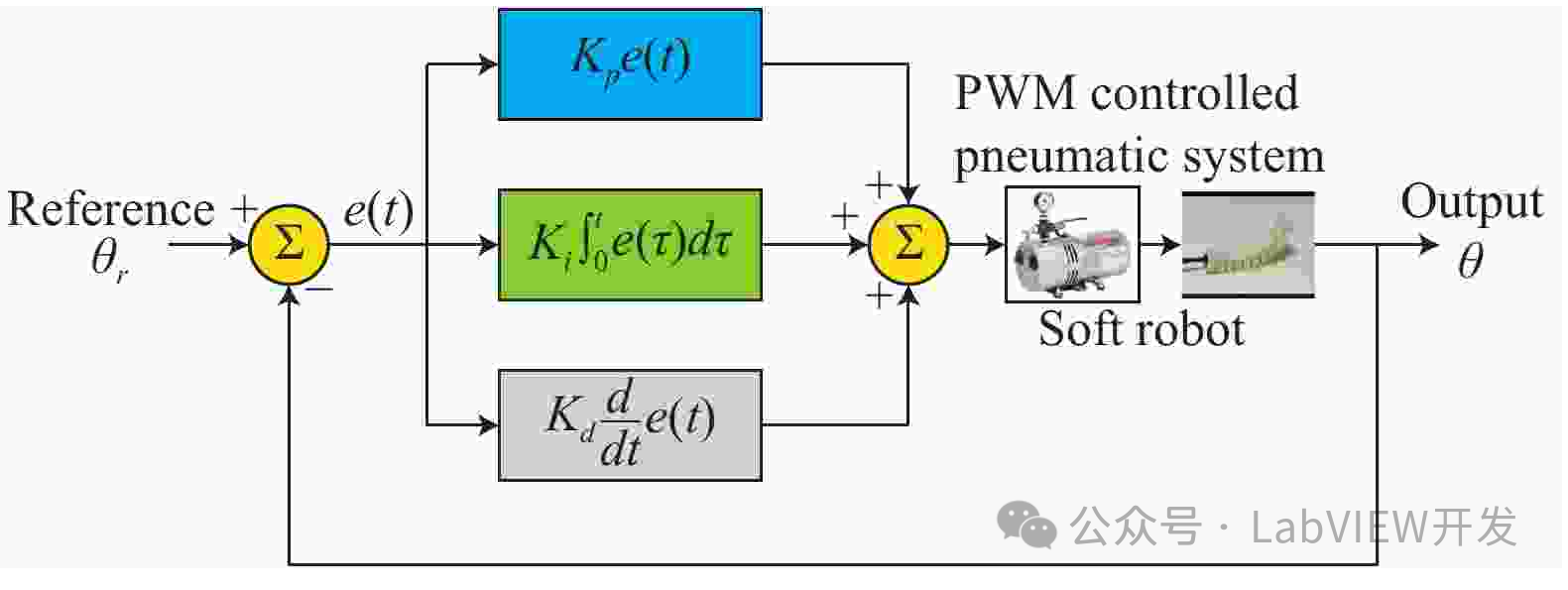
LabVIEW中PID控制器系统的噪声与扰动抑制策略
在LabVIEW中处理PID控制器系统中的噪声和外部扰动,需要从信号处理、控制算法优化、硬件滤波和系统设计四个角度入手。采用滤波技术、调节PID参数、增加前馈控制和实施硬件滤波器等方法,可以有效减少噪声和扰动对系统性能的影响,提高控制系统的…...
JavaWeb笔记整理+图解——Listener监听器
欢迎大家来到这一篇章——Listener监听器 监听器和过滤器都是JavaWeb服务器三大组件(Servlet、监听器、过滤器)之一,他们对于Web开发起到了不可缺少的作用。 ps:想要补充Java知识的同学们可以移步我已经完结的JavaSE笔记&#x…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

spring Security对RBAC及其ABAC的支持使用
RBAC (基于角色的访问控制) RBAC (Role-Based Access Control) 是 Spring Security 中最常用的权限模型,它将权限分配给角色,再将角色分配给用户。 RBAC 核心实现 1. 数据库设计 users roles permissions ------- ------…...

前端调试HTTP状态码
1xx(信息类状态码) 这类状态码表示临时响应,需要客户端继续处理请求。 100 Continue 服务器已收到请求的初始部分,客户端应继续发送剩余部分。 2xx(成功类状态码) 表示请求已成功被服务器接收、理解并处…...

接口 RESTful 中的超媒体:REST 架构的灵魂驱动
在 RESTful 架构中,** 超媒体(Hypermedia)** 是一个核心概念,它体现了 REST 的 “表述性状态转移(Representational State Transfer)” 的本质,也是区分 “真 RESTful API” 与 “伪 RESTful AP…...
