C语言王国——杨氏矩阵
目录
1. 引言
2. 了解杨氏矩阵
3. 思路分析
4. 代码
5. 总结
1. 引言
最近在做二维数组的训练的时候发现了一个很有意思的题:

一看这不是杨氏矩阵嘛,接下来就由姜糖我带大家了解一下这个著名的矩阵。
2. 了解杨氏矩阵
通过查阅百度得知:
杨氏矩阵:
是对组合表示理论和舒伯特演算很有用的工具。它提供了一种方便的方式来描述对称和一般线性群的群表示,并研究它们的性质。有一个二维数组. 数组的每行从左到右是递增的,每列从上到下是递增的. 在这样的数组中查找一个数字是否存在。 时间复杂度小于O(N)。
平常我们在数组里查找数字时,是否我们用的都是暴力遍历查找,一个数一个数的去比对时间复杂度为O(n),效率很低,这时候就该我们杨氏矩阵出场了。
3. 思路分析
资料中我们知道了杨氏矩阵是一个二维数组,数组的每行从左到右是递增的,每列从上到下是递增的. 在这样的数组中查找一个数字是否存在,所以我们举一个例子:
在arr[3][3] = {{1,2,3},{4,5,6},{7,8,9}}查找数字n。
数组如图:

此数组符合杨氏矩阵。
那接下来我们该怎么查找数字更快捷呢。接下来我们要找此数组里的特殊的数,我们会发现最右上角的那个数是一行之中最大的一列之中最小的所以我们拿n去跟他比较,然后我们就会发现:

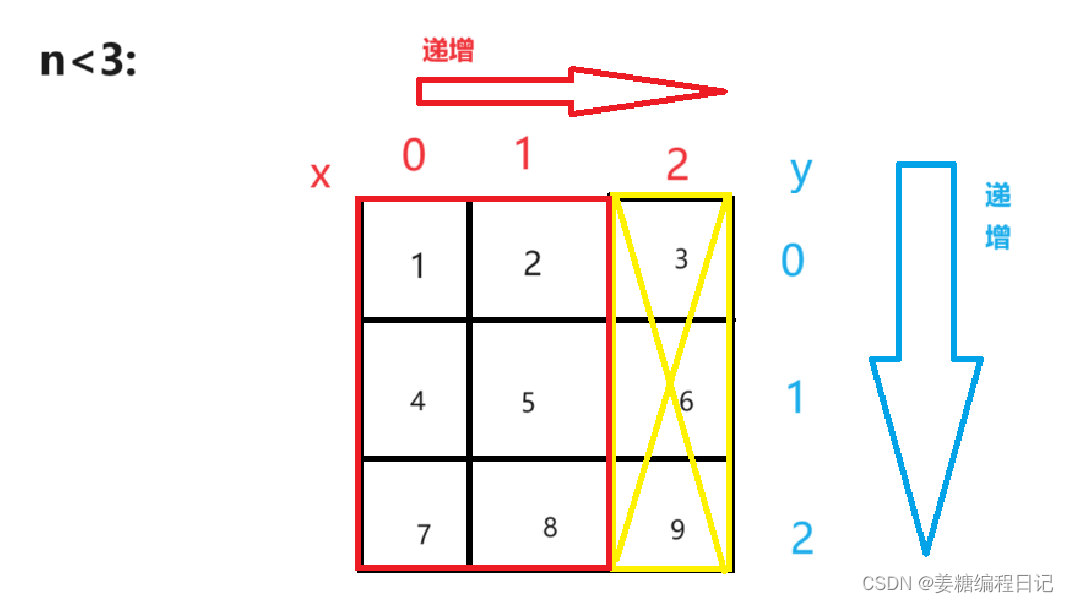
红色为查找范围,黄色为除去范围。
根据图中我们发现当n>3时,第一行就被排除了,查找范围只有第二、三行;
当n<3时,第一列就被排除了 ,查找范围只有第二、三列。
然后在接下来的图像中继续取右上角的数字进行比较,排除行和列直达剩下查找的数,若都找不到则数字n不在数组中。
我们将n赋值进行具体分析,为了特殊性,我们就取右上角的对角左下角7吧。
当n=7,如图分析:

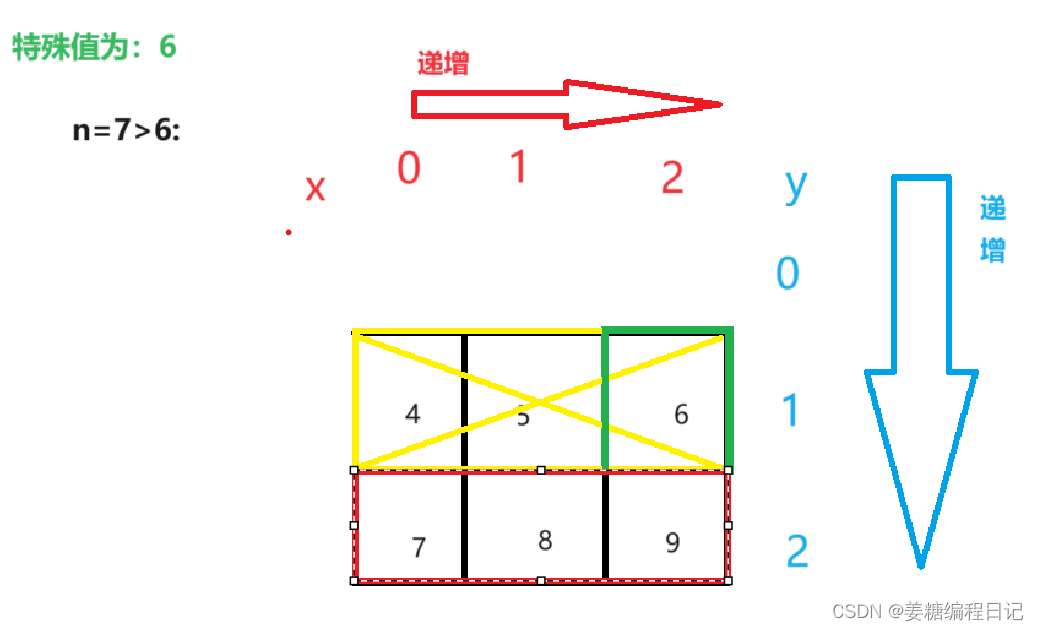
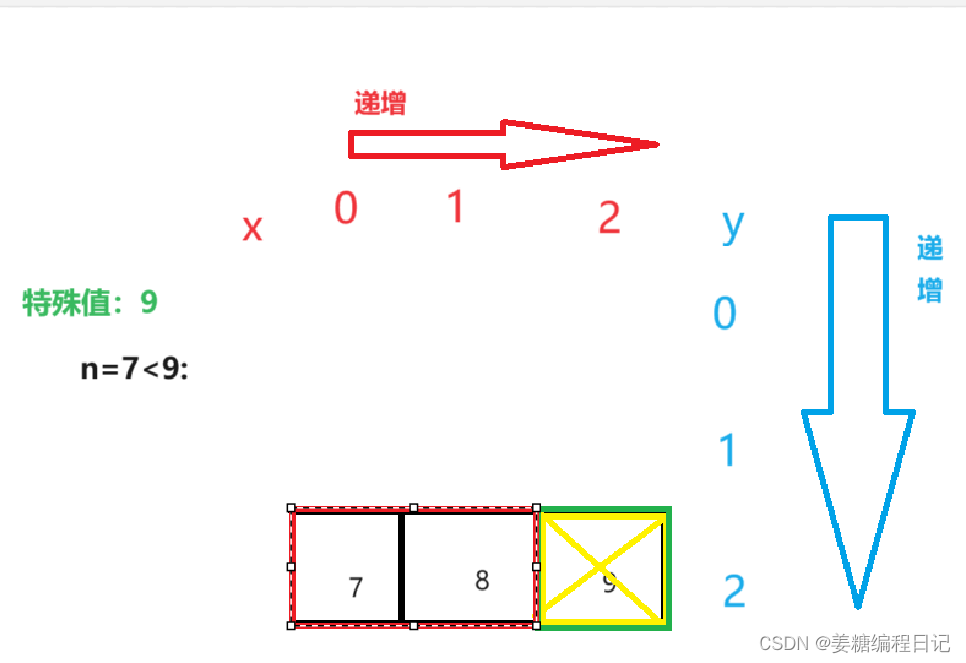
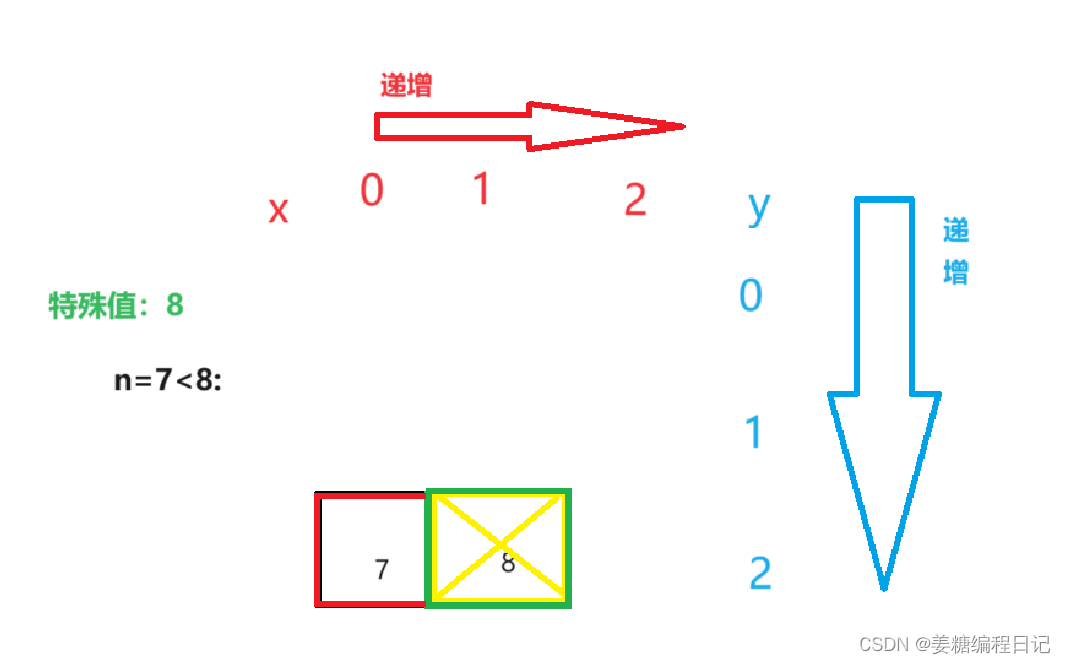

这样我们就能找到我们的数字n了。最后我们也发现:在一个杨氏矩阵中查找最特殊的数字7,我们总共进行了5次比较,找到了元素,这样的查找方式明显比遍历二维数组的效率高 。
4. 代码
接下来我就来分享一下我写的代码:
#include<stdio.h>int young(int (*arr)[3], int n)
{int i,j = 0;for (i = 0; i < 3; i++){for (j = 2; j >= 0; j--){if (n == arr[i][j]){return 1;}else if(n > arr[i][j]){break;}}}return 0;}int main()
{int arr[3][3] = { 1,2,3,4,5,6,7,8,9 };printf("输入你要查找的数字:");int n = 0;scanf("%d", &n);int ret = young(arr, n);if (n){printf("找到了");}elseprintf("找不到");return 0;
但是我们发现这样子的代码只能判断是否找到数字,不能判断数字的位置,所以我给代码进行了优化:
#include<stdio.h>int young(int(*arr)[3], int* px, int* py, int n)
{int y = *py;int x = *px-1;for (*py = 0; *py < y; (*py)++){for (*px = x; (*px) >= 0; (*px)--){if (n == arr[(*py)][(*px)]){return 1;}else if (n > arr[*py][*px]){break;}}}return 0;
}int main()
{int arr[3][3] = { 1,2,3,4,5,6,7,8,9 };printf("输入你要查找的数字:");int n = 0;scanf("%d", &n);int i = 3;int j = 3;int ret = young(arr, &i , &j , n);if (n){printf("找到了为arr[%d][%d]",j,i);}elseprintf("找不到");return 0;
}像这样子我们把数组行和列用指针的形式传到函数里去,随着函数的变化去变化最后就能得到数组中我们要查找的n的位置。
最后我们发现用while循环思路会更清晰准确:
#include<stdio.h>
int find_num(int arr[3][3], int* px, int* py, int k)
{int x = 0;int y = *py - 1;while (x < *px && y >= 0){//向下查找if (k > arr[x][y]){x++;}//向左查找else if (k < arr[x][y]){y--;}//找到了else{*px = x;*py = y;return 1;}}return 0;
}
int main()
{int arr[3][3] = { 1,2,3,4,5,6,7,8,9 };int k = 0;scanf("%d", &k);int x = 3;int y = 3;int ret = find_num(arr, &x, &y, k);if (ret == 1){printf("找到了,下标是%d %d\n", x, y);}else{printf("找不到\n");}return 0;
}5. 总结
如果大家有不同见解也可以私信姜糖哦,姜糖也在不停的学习进步,与大家一起步入大牛之列。期待大家三连!!
相关文章:

C语言王国——杨氏矩阵
目录 1. 引言 2. 了解杨氏矩阵 3. 思路分析 4. 代码 5. 总结 1. 引言 最近在做二维数组的训练的时候发现了一个很有意思的题: 一看这不是杨氏矩阵嘛,接下来就由姜糖我带大家了解一下这个著名的矩阵。 2. 了解杨氏矩阵 通过查阅百度得知: …...

陪玩小程序都需要怎么做?
开发陪玩小程序需要进行全面的需求分析、功能规划、技术选型、界面设计等一系列步骤。陪玩小程序作为一种新兴的网络服务平台,为用户提供了寻找游戏伙伴、预约陪玩服务等功能,满足了用户在游戏领域的社交互动和技能提升需求。具体分析如下: 需…...
)
postgressql——子事务可见性判断 性能问题(8)
子事务可见性判断 & 性能 测试SQL BEGIN; PREPARE sel(integer) ASSELECT count(*)FROM contendWHERE id BETWEEN $1 AND $1 + 100; PREPARE upd(integer) ASUPDATE contend SET val = val + 1WHERE id IN ($1, $1 + 10, $1 + 20, $1 + 30);SAVEPOINT a; \set rnd random…...

20240531在飞凌的OK3588-C开发板上跑原厂的Buildroot测试USB摄像头
20240531在飞凌的OK3588-C开发板上跑原厂的Buildroot测试USB摄像头 2024/5/31 20:04 USB摄像头分辨率:1080p(1920x1080) 默认编译Buildroot的SDK即可点亮USB摄像头。v4l2-ctl --list-devices v4l2-ctl --list-formats-ext -d /dev/video74 …...

从0开始学统计-什么是回归?
1.什么是回归? 回归(Regression)是统计学中一种用于探索变量之间关系的分析方法。它主要用于预测一个或多个自变量(输入变量)与因变量(输出变量)之间的关系。在回归分析中,我们尝试根…...
Element-ui使用上传时弹框选择文件类型
实现效果 1,点击上传,上传文件; 2,选择文件; 3,弹框选择文件类型; 4,选择类型后确定上传; 一,上传 跳过; 二,定义弹框下拉框…...

原生小程序一键获取手机号
1.效果图 2.代码index.wxml <!-- 获取手机号 利用手机号快速填写的功能,将button组件 open-type 的值设置为 getPhoneNumber--><button open-type"getPhoneNumber" bindgetphonenumber"getPhoneNumber">获取手机号</button> …...
ARM虚拟机安装OMV
OMV(OpenMediaVault)是基于 Debian GNU/Linux 的网络连接存储(network attached storage,NAS)解决方案。它包含 SSH、(S) FTP、SMB/CIFS、DAAP 媒体服务器、rsync、 BitTorrent 等很多种服务。它可用于 x86-64 和 ARM 平台。 在x86-64平台上&…...

【协议开发系列】梳理关于TCP和UDP两种协议的区别和使用场景
起源 前二天项目上在核对外部对接服务的五元组列表的时候,有一位客户提问对于同样的服务同时支持tcp和udp二种方式,有什么优点和缺点,应该如何选择?这个问题突然让我愣了一下,确实好久没有“温故”了,相关…...

vue blob实现自定义多sheet数据导出到excel文件
背景:最近vue项目遇到一个需求,就是需要将多个表格分成不同sheet页并导出,之前的工具类只能导出一个sheet页,所以在原有的基础上,调整一下,让它支持多sheet导出。 vue blob文件流,这个肯定要的…...

Python—面向对象小解(3)
一、多态 多态指的是一类事物的多中形态 相同的方法,产生不同的执行结果 运算符 * 的多态 int int 加法计算 str str 字符串拼接 list list 列表的数据合并 在python中可以使用类实现一个多态效果 在python中使用重写的方式实现多态 (1)定…...

Nginx超时时间
Nginx是一款自由、开源、高性能的HTTP和反向代理服务器,它可以通过不同的设置来提高网站的性能和安全性。其中,设置Nginx超时时间非常重要,因为它将直接影响网站的响应速度和用户体验。本文将从多个方面详细阐述Nginx超时时间的设置方法与注意…...

Imgs,GT,Edge,Gradient_all,Gradient_Foreground
保存一下: 做个记录: import cv2 import os import numpy as np# 对整张图片做canny检测 得到纹理图 def canny_all(input_path, output_path):# 遍历文件夹中的所有文件for filename in os.listdir(input_path):# 构造完整的文件路径image_path os.p…...

自学成才Flutter 弹性布局、线性布局
本文我们要介绍 Flutter 中布局 Widget,包括弹性布局、线性布局 流式布局和层叠布局。 Flutter中文网 Flutter开发 一、弹性布局--Flex Flex 类似 Android 中的 FlexboxLayout,和 Expanded 配合使用可以实现子Widget 按照一定比例来分配父容器空间。 使…...
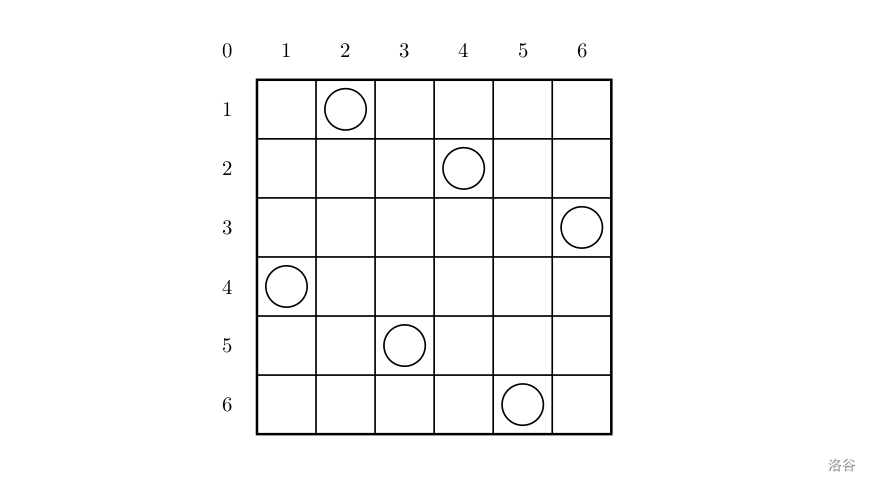
Part 3.1 深度优先搜索
深度优先搜索(DFS),即按照深度优先的顺序搜索的算法。 深度优先搜索一般使用栈来实现。 [USACO1.5] 八皇后 Checker Challenge 题目描述 一个如下的 6 6 6 \times 6 66 的跳棋棋盘,有六个棋子被放置在棋盘上,使得…...
前端Vue小兔鲜儿电商项目实战Day03
一、Home - 整体结构搭建和分类实现 1. 页面结构 ①按照结构新增5个组件,准备最简单的模板,分别在Home模块的入口组件中引入 src/views/Home/components/ HomeCategory.vue HomeBanner.vue HomeNew.vue HomeHot.vue HomeProduct.vue <script …...

ORACLE 查询SQL优化
1 使用EXPLAIN PLAN 使用EXPLAIN PLAN查看查询的执行计划,这可以帮助你理解查询是如何被Oracle执行的。基于执行计划,你可以确定是否存在索引缺失、不必要的全表扫描等问题。 以下是几种使用EXPLAIN PLAN的方法: 使用EXPLAIN PLAN FOR: 你可以…...
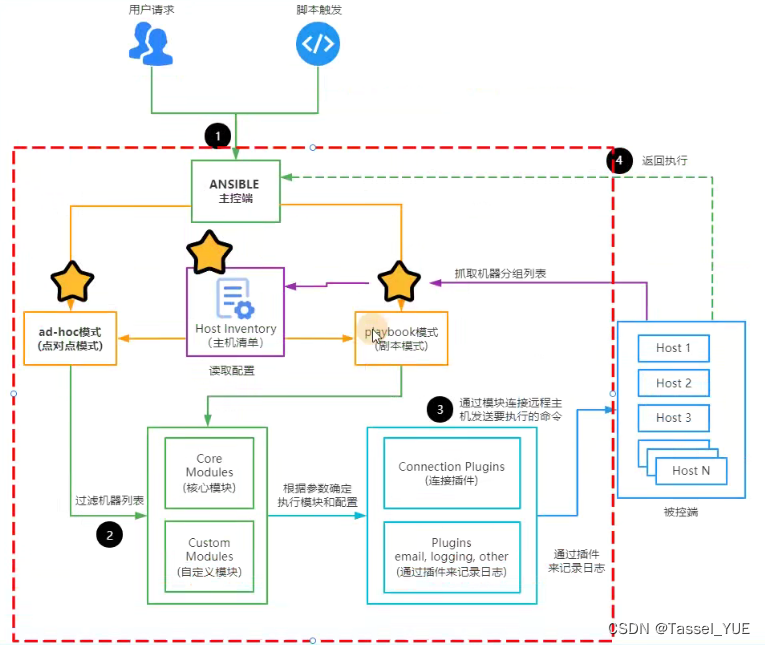
Ansible03-Ansible Playbook剧本详解
目录 写在前面5. Ansible Playbook 剧本5.1 YAML语法5.1.1 语法规定5.1.2 示例5.1.3 YAML数据类型 5.2 Playbook组件5.3 Playbook 案例5.3.1 Playbook语句5.3.2 Playbook1 分发hosts文件5.3.3 Playbook2 分发软件包,安装软件包,启动服务5.3.3.1 任务拆解…...

Qt-qrencode生成二维码
Qt-qrencode开发-生成二维码📀 文章目录 Qt-qrencode开发-生成二维码📀[toc]1、概述📸2、实现效果💽3、编译qrencode🔍4、在QT中引入编译为静态库的QRencode5、在Qt中直接使用QRencode源码6、在Qt中使用QRencode生成二…...
)
长安链使用Golang编写智能合约教程(三)
本篇主要介绍长安链Go SDK写智能合约的一些常见方法的使用方法或介绍 资料来源: 官方文档官方示例合约库 官方SDK接口文档 教程一:智能合约编写1 教程二:智能合约编写2 一、获取参数、获取状态、获取历史记录的方法解析 注意! …...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

pgsql:还原数据库后出现重复序列导致“more than one owned sequence found“报错问题的解决
问题: pgsql数据库通过备份数据库文件进行还原时,如果表中有自增序列,还原后可能会出现重复的序列,此时若向表中插入新行时会出现“more than one owned sequence found”的报错提示。 点击菜单“其它”-》“序列”,…...
Element-Plus:popconfirm与tooltip一起使用不生效?
你们好,我是金金金。 场景 我正在使用Element-plus组件库当中的el-popconfirm和el-tooltip,产品要求是两个需要结合一起使用,也就是鼠标悬浮上去有提示文字,并且点击之后需要出现气泡确认框 代码 <el-popconfirm title"是…...
)
Electron简介(附电子书学习资料)
一、什么是Electron? Electron 是一个由 GitHub 开发的 开源框架,允许开发者使用 Web技术(HTML、CSS、JavaScript) 构建跨平台的桌面应用程序(Windows、macOS、Linux)。它将 Chromium浏览器内核 和 Node.j…...

如何在Spring Boot中使用注解动态切换实现
还在用冗长的if-else或switch语句管理多个服务实现? 相信不少Spring Boot开发者都遇到过这样的场景:需要根据不同条件动态选择不同的服务实现。 如果告诉你可以完全摆脱条件判断,让Spring自动选择合适的实现——只需要一个注解,你是否感兴趣? 本文将详细介绍这种优雅的…...
)
板凳-------Mysql cookbook学习 (十--2)
5.12 模式匹配中的大小写问题 mysql> use cookbook Database changed mysql> select a like A, a regexp A; ------------------------------ | a like A | a regexp A | ------------------------------ | 1 | 1 | --------------------------…...
