人眼是如何看到物体的
我在试图理解人眼如何观察到物体的,发现没有解释。本来我想这应该跟照相机照相的结果一样,但是发现,照相机也不对劲,没有理由能成像啊。
因为物体在散射光的时候,假设散射的光在局部是平行光,那么物体散射的平行光有无数组,这无数组中到达眼睛的光也是无数组,那么眼睛应该选择哪一组光呢?我只是为了引出问题,而说出是那一组,实际情况应该这样建立数学关系,假设用亮度L表示物体反射出来的光,物体的位置为x,表示一个点,物体是一个曲面S。F(x):S->LxD, D表示光的方向,在空间中的方向是三个参数的。空间曲面S是两个参数的。 L是亮度,包含于R+中。
而人的眼睛当成是个大洞O,只有通过这个O的光线会被眼睛捕捉,然后给感受器。
能通过O的光线F受到物体的点x和O中心位置o,和半径,和洞所在平面与x轴的夹角。O是平面上的洞。可以假设这是个约束条件g(O, S)<=0,至于是不等式的原因简单,因为在边界是等于0,但是在圆内也满足需要,所以约束为这个。
问题就是在约束条件下,如何选择眼睛感受器得到的光线H(S1), S1表示感受器的定义域。
再定义函数H:SxD->O,表示从S位置和D方向的光线射到了O内的某个位置。
实际上,对于圆O内的任意一个位置y,对于曲面S内的任意一个位置x,散射光中存在某个方向d,使得H(x,d)=y。这意味着这个洞的每个位置,都接收到了曲面S的每个位置x的光,但是要看到图像,只能在这个洞的每个位置o上选择曲面S的x位置的光,即是x(o)是函数。
这就是等价类的思想了。对于S中的任意位置x,如何做到让满射到O上的发散光再次汇聚到空间上一点z呢?如果能够做到还需要进一步考虑: 随着x连续移动,汇聚到一点的位置z也是连续不重复的移动的,这就是同胚,当光路是可逆的时候。同胚得到的是曲面S1,就是感受器的感光曲面。
这个感光曲面S1的每一个点z, 和S的x是一一对应的。那么O就变成了散射光的裁剪窗口,而之后的光线汇聚了,那么这个聚点的光线的亮度是极强的。
在物理中,是如何做到汇聚光线的呢?就是费马原理。
如果想要光线汇聚于一点z,也就是x上射入裁剪窗口O的所有光线汇聚于z点,那么需要任意路径的光程是恒等的。而xz之间的光程,就是费马原理确定的。
变分法是求极值的方法,所以假设充满xz之间空间的所有介质的折射率都确定了,那么可以利用费马原理求出来xz的极小的光程,或者极大的光程,这是由介质决定的,一般如果只空气介质那就是极短光程。已知光程,也无法直接得到光的路径,因为光程是实数。
但是变分法,不是求光程的,而是求光的路径的。已知折射率了,很容易求出来光的路径。
一个简单的事实是透镜可以做到,如何证明物点Q和像点Q'之间,任意从Q发散的光通过透镜O,都能达到Q'才合理。此时O不是平面中的裁剪窗口了,而是空间上的凸集,这并没有多大的影响。
如何证明透镜能够做到呢? 这需要对透镜的几何形状用函数表示出来,还需要空气和透镜的折射率均给出,然后对于透镜另一侧的位置y利用费马原理求出光路径这个不重要,然后是移动y到某个点z,使得光程r(a)常数,那么这个z就是所说的像点,能够汇聚到达透镜O的所有光线。
关键是不知道如何得到凸透镜的曲面公式,之后的计算就无法建立了。
但是我说一下可能性,原本到达z的穿过平面O的所有光线a的光程r1(a)是连续的,要使得通过在xz之间的裁剪圆位置添加透镜,使得r1(a)为常数,这相当于对曲线r1(a)进行横向拉直操作,至少透镜是个连续函数,可以认为是从原本插入的是0函数逐渐过渡成为透镜函数,这个过程是连续变化的,无法计算就不多说这部分的内容了。
总结就是透镜使得成像成为了可能。因为它把裁剪窗口的光线全部汇聚到了一点。
附加说明一点: 小孔成像的原理。
小孔成像是因为裁剪窗口非常小,使得物体S的某个位置x的发散光,近乎平行光映射到O上,在后面成像的时候,会有一点模糊,毕竟是点放大了一些。所有的点成像都有放大一些,但是只要小孔足够小,光线越接近平行,成像位置接近小孔,这种模糊范围越小。
相关文章:

人眼是如何看到物体的
我在试图理解人眼如何观察到物体的,发现没有解释。本来我想这应该跟照相机照相的结果一样,但是发现,照相机也不对劲,没有理由能成像啊。 因为物体在散射光的时候,假设散射的光在局部是平行光,那么物体散射…...
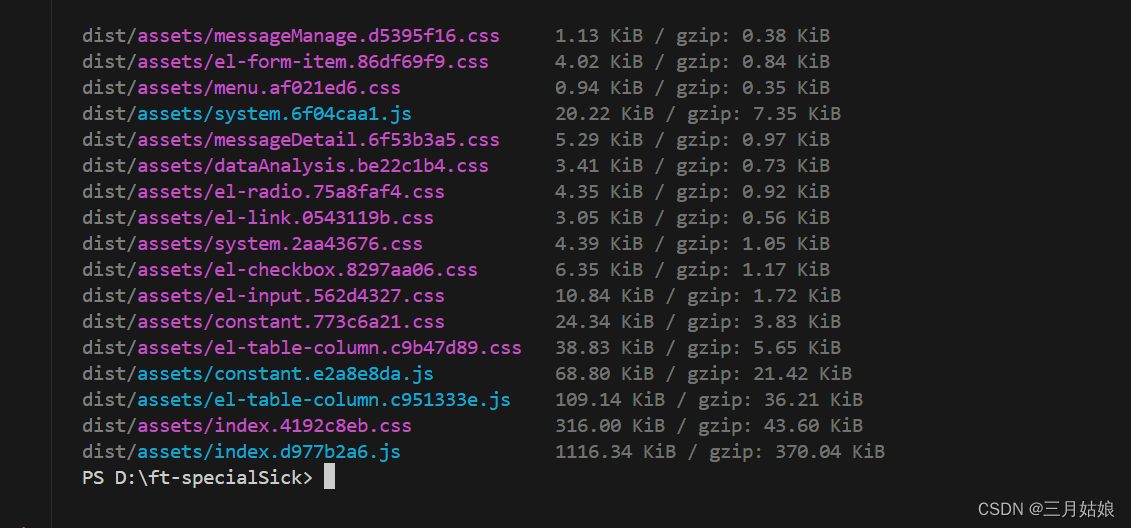
vue打包时报错文件包过大
1.问题:npm run build 之后出现 2. 翻译之后意思就是某块过大 3. 解决办法:在vite.config.ts文件上添加 build: { chunkSizeWarningLimit: 1600, }, 4.最终打包...

预编码算法(个人总结)
引言 预编码算法是现代无线通信系统中的关键技术,特别是在多输入多输出(MIMO)系统中。它们通过在发送端对信号进行处理,减少干扰并提高信道容量。这种技术广泛应用于5G、Wi-Fi和卫星通信系统中。本教程将详细介绍预编码算法的背景…...

【重学C语言】十七、预处理指令
【重学C语言】十七、预处理指令 预处理指令预定义宏`#define` 宏定义示例注意事项特殊符号条件编译头文件包含`#pragma`预处理指令 C语言中的预处理指令(Preprocessor Directives)是一种特殊的指令,它们在编译过程的早期阶段(即实际编译之前)被预处理器(Preprocessor)处…...

SQL注入的危害和原理
在Web应用开发中,SQL注入是一种常见的安全漏洞,它允许攻击者通过注入恶意的SQL语句来执行非法操作,甚至获取敏感数据。本篇博客将详细解释SQL注入的危害和原理,并提供一些解决方案,以帮助新人快速理解并避免这种安全威…...
Unity2D横版摄像机跟随
在Unity2D横版游戏中,摄像机跟随是一个非常重要的功能。一个流畅的摄像机跟随系统可以让玩家更好地沉浸在游戏世界中。本文将介绍如何在Unity中实现2D横版摄像机跟随,并分享一些优化技巧。 一、准备工作 在开始实现摄像机跟随之前,请确保您…...

Practicing Version Control
Part A 新建一个文件夹Git,然后进入文件夹: Windows: 在这个文件夹中右键 > Open Git Bash hereMac: 运行终端,打cd 空格,然后将文件夹拖入终端,按 return 从 Github 上复制 HTTPS,然后 git clone https://githu…...
新宏观范式和产业趋势下,纷享销客如何助力企业出海?
出海,已不再是企业的“备胎”,而是必须面对的“大考”!在这个全球化的大潮中,有的企业乘风破浪,勇攀高峰,也有的企业在异国他乡遭遇了“水土不服”。 面对“要么出海,要么出局”的抉择ÿ…...

安装zookeeper
一、搭建前准备 192.168.1.99 sdw1 192.168.1.98 sdw2 192.168.1.97 sdw3 二、搭建 1、各主机修改/etc/hosts,/etc/hostname文件 /etc/hosts 127.0.0.1 localhost localhost.localdomain localhost4 localhost4.localdomain4 ::1 localhos…...

深入分析 Android Activity (二)
文章目录 深入分析 Android Activity (二)1. Activity 的启动模式(Launch Modes)1.1 标准模式(standard)1.2 单顶模式(singleTop)1.3 单任务模式(singleTask)1.4 单实例模式…...
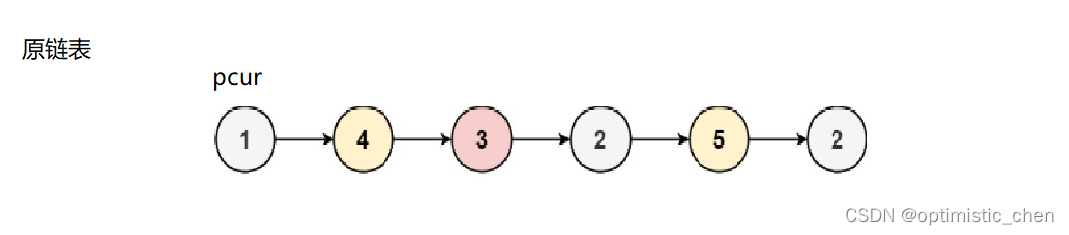
数据结构——经典链表OJ(二)
乐观学习,乐观生活,才能不断前进啊!!! 我的主页:optimistic_chen 我的专栏:c语言 点击主页:optimistic_chen和专栏:c语言, 创作不易,大佬们点赞鼓…...

文件IO(三)
文件IO(三) 左移右移Linux的man 手册文件IO打开文件操作文件关闭文件 caps lock开灯关灯读取按键文件IO操作目录文件打开目录文件操作目录文件 库动态库和静态库的优缺点创建静态库创建动态库 按下右ctrl键 亮灭灯 左移右移 Linux的man 手册 文件IO 打开…...
单实例11.2.0.3迁移到RAC11.2.0.4_使用RMAN 异机恢复
保命法则:先备份再操作,磁盘空间紧张无法备份就让满足,给自己留退路。 场景说明: 1.本文档的环境为同平台、不同版本(操作系统版本可以不同,数据库小版本不同),源机器和目标机器部…...

JavaScript第四讲:函数,作用域,运算符
前言 在JavaScript的广阔天地中,函数、作用域、算术运算符和逻辑运算符是构成代码世界的基石。它们各自扮演着不同的角色,却又紧密相连,共同编织出丰富多彩的程序逻辑。无论是编写一个简单的网页交互,还是构建一个复杂的应用程序…...
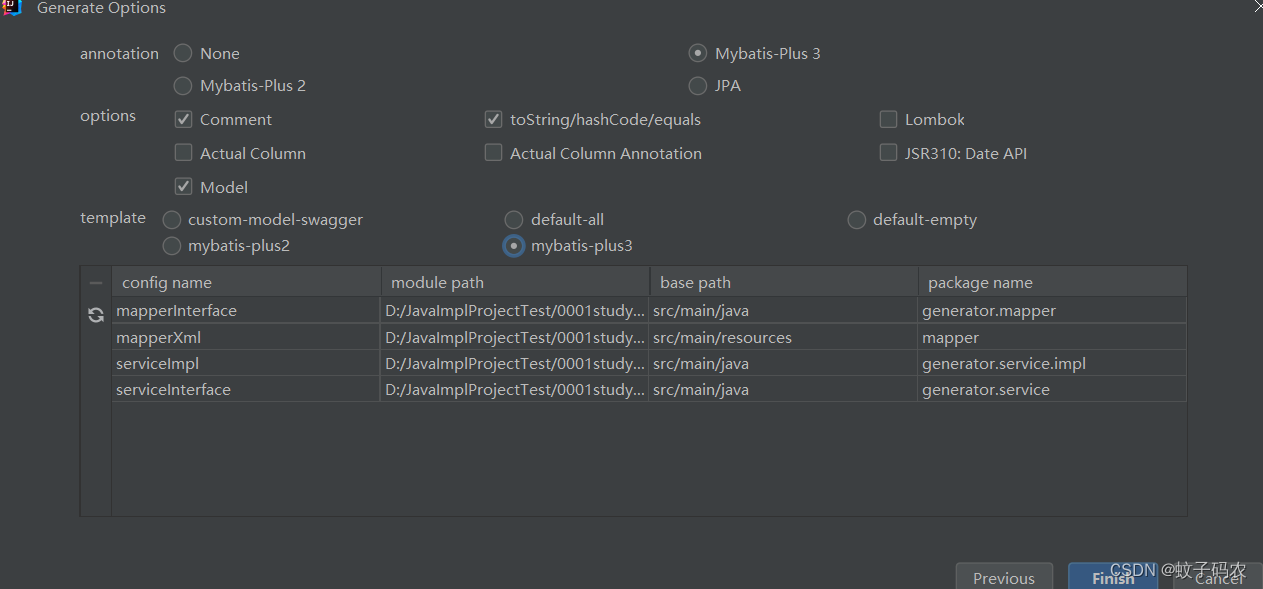
IDEA中,MybatisPlus整合Spring项目的基础用法
一、本文涉及的知识点【重点】 IDEA中使用MybatisPlus生成代码,并使用。 Spring整合了Mybatis框架后,开发变得方便了很多,然而,Mapper、Service和XML文件,在Spring开发中常常会重复地使用,每一次的创建、修…...

从不同角度看如何让大模型变得更聪明呢?
算法创新,从代码上优化大模型,可以采取一系列策略来提升其性能和效率。 算法优化:对模型的算法进行精细调整,如改进神经网络架构,使用更高效的层(如深度可分离卷积),或者优化递归神经…...

Buffer Pool运行机制理解
Buffer Pool机制理解 一、为什么使用Buffer Pool? 众所周知,磁盘数据是以数据页的形式来去读取的,一个数据页默认大小 16K,也就是说你本意只想读取一行数据,但是它会给你加载一页的数据到buffer pool里面。这样的话就…...
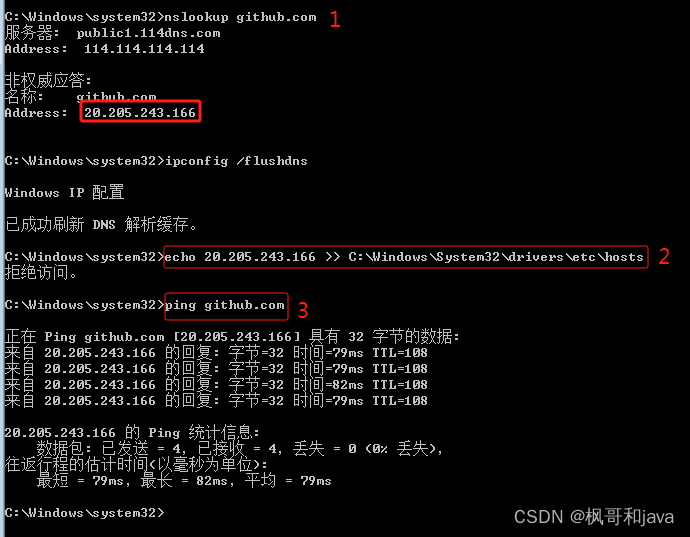
windows配置dns访问git , 加快访问速度保姆级教程
设置 DNS 访问 Git 需要修改电脑的 DNS 配置。下面是具体的操作流程: 第一步:打开命令提示符或终端窗口 在 Windows 系统中,可以按下 Win R 组合键,然后输入 “cmd”,按下 Enter 键打开命令提示符窗口。在 macOS 或 …...

Solidity学习-投票合约示例
以下的合约有一些复杂,但展示了很多Solidity的语言特性。它实现了一个投票合约。 当然,电子投票的主要问题是如何将投票权分配给正确的人员以及如何防止被操纵。 我们不会在这里解决所有的问题,但至少我们会展示如何进行委托投票,…...
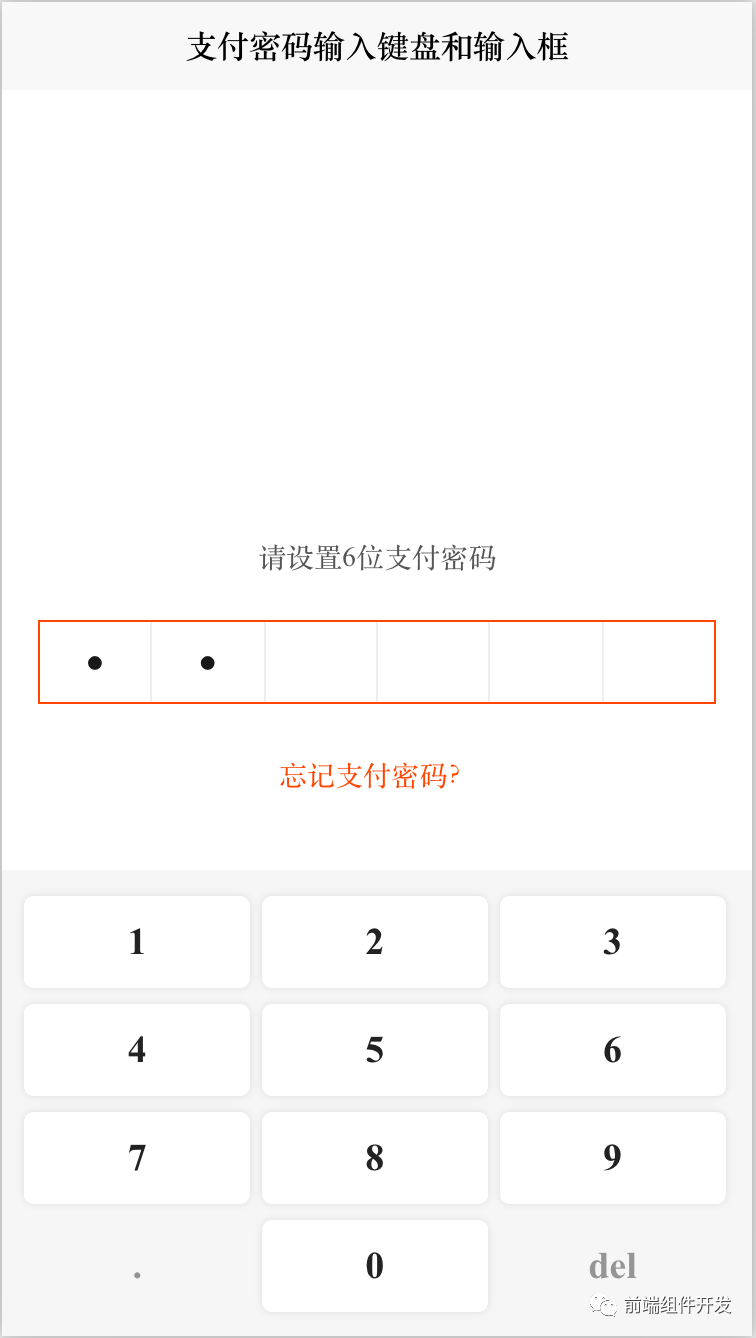
前端Vue自定义支付密码输入框键盘与设置弹框组件的设计与实现
摘要 随着信息技术的不断发展,前端开发的复杂性日益加剧。传统的开发方式,即将整个系统构建为一个庞大的整体应用,往往会导致开发效率低下和维护成本高昂。任何微小的改动或新功能的增加都可能引发对整个应用逻辑的广泛影响,这种…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现指南针功能
指南针功能是许多位置服务应用的基础功能之一。下面我将详细介绍如何在HarmonyOS 5中使用DevEco Studio实现指南针功能。 1. 开发环境准备 确保已安装DevEco Studio 3.1或更高版本确保项目使用的是HarmonyOS 5.0 SDK在项目的module.json5中配置必要的权限 2. 权限配置 在mo…...
