ModuleNotFoundError: No module named ‘pip‘
项目场景:pip 错误
Traceback (most recent call last):
File "E:\KaiFa\Python\Python38\lib\runpy.py", line 194, in _run_module_as_main
return _run_code(code, main_globals, None,
File "E:\KaiFa\Python\Python38\lib\runpy.py", line 87, in _run_code
exec(code, run_globals)
File "E:\KaiFa\Python\Python38\Scripts\pip.exe\__main__.py", line 4, in <module>
ModuleNotFoundError: No module named 'pip'
问题描述
执行pip 就报错
python -m pip install --upgrade pip原因分析:
pip文件内部有错误
解决方案:
删除掉pip文件夹解决
Python\Python38\Lib\site-packages\里面的pip开头的文件删掉
再执行: python -m ensurepip
相关文章:

ModuleNotFoundError: No module named ‘pip‘
项目场景:pip 错误 Traceback (most recent call last): File "E:\KaiFa\Python\Python38\lib\runpy.py", line 194, in _run_module_as_main return _run_code(code, main_globals, None, File "E:\KaiFa\Python\Python38\lib\runpy.py&qu…...
)
ROS2 入门应用 发布和订阅(C++)
ROS2 入门应用 发布和订阅(C)1. 创建功能包2. 创建源文件2.1. 话题发布2.2. 话题订阅3. 添加依赖关系4. 添加编译信息4.1. 添加搜索库4.2. 增加可执行文件4.3. 增加可执行文件位置5. 编译和运行1. 创建功能包 在《ROS2 入门应用 工作空间》中已创建和加…...

XSS漏洞,通过XSS实现网页挂马
**今天讲下通过XSS实现网页挂马~*,目的是了解安全方面知识,提升生活网络中辨别度 原理: 实验分为两部分: 1、通过Kali linux,利用MS14_064漏洞,制作一个木马服务器。存在该漏洞的用户一旦通过浏览器访问木…...
家政服务小程序实战教程09-图文卡片
小程序还有一类需求就是展示服务的列表,我们这里用图文卡片组件来实现,我们先要添加一个标题,使用网格布局来实现 第一列添加一个文本组件,第二列添加一个图标组件 修改文本组件的文本内容,设置外边距 设置第二列的样式…...
国内唯一一部在CentOS下正确编译安装和使用RediSearch的教程
开篇 Redis6开始增加了诸多激动人心的模块,特别是:RedisJSON和RediSearch。这两个模块已经完全成熟了。它们可以直接使用我们的生产上的Redis服务器来做全文搜索(二级搜索)以取得更廉价的硬件成本、同时在效率上竟然超过了Elastic…...

前端对于深拷贝和浅拷贝的应用和思考
浅拷贝 浅拷贝 : 浅拷贝是指对基本类型的值拷贝,以及对对象类型的地址拷贝。它是将数据中所有的数据引用下来,依旧指向同一个存放地址,拷贝之后的数据修改之后,也会影响到原数据的中的对象数据。最简单直接的浅拷贝就…...

Java基础常见面试题(三)
String 字符型常量和字符串常量的区别? 形式上: 字符常量是单引号引起的一个字符,字符串常量是双引号引起的若干个字符; 含义上: 字符常量相当于一个整型值( ASCII 值),可以参加表达式运算;字符串常量代表一个地址值…...
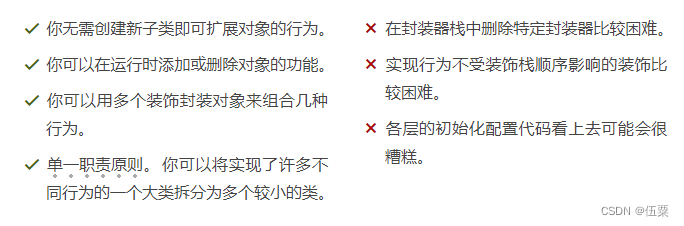
C++设计模式(13)——装饰模式
亦称: 装饰者模式、装饰器模式、Wrapper、Decorator 意图 装饰模式是一种结构型设计模式, 允许你通过将对象放入包含行为的特殊封装对象中来为原对象绑定新的行为。 问题 假设你正在开发一个提供通知功能的库, 其他程序可使用它向用户发…...
ESP-01S通过AT指令上报数据到阿里云物模型
ESP-01S使用AT指令上报数据到阿里云物模型 上篇文章介绍了如何用AT指令连接阿里云并进行通信:https://blog.csdn.net/weixin_46251230/article/details/128995530 但最终需要将传感器数据上报到云平台显示,所以需要建立阿里云物模型 阿里云平台建立物…...
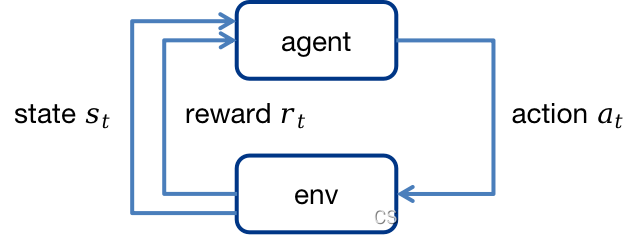
【强化学习】马尔可夫决策过程MDP
1.马尔可夫决策过程MDP 1.1 MDP五元组 MDP<S,A,P,R,γ>MDP<\mathcal{S},\mathcal{A},\mathcal{P},\mathcal{R},\mathcal{\gamma}>MDP<S,A,P,R,γ>,其中: S\mathcal{S}S:状态空间A\mathcal{A}A:动作空间P\mathc…...

刘润:五维思考,让你站得更高、看得更远
原标题:刘润:五维思考,让你站得更高、看得更远 前言:遇到问题时,有的人很快就能想明白,有的人需要很久才能想明白,还有的人始终都想不明白。 而且,那些很快就能想明白的人࿰…...
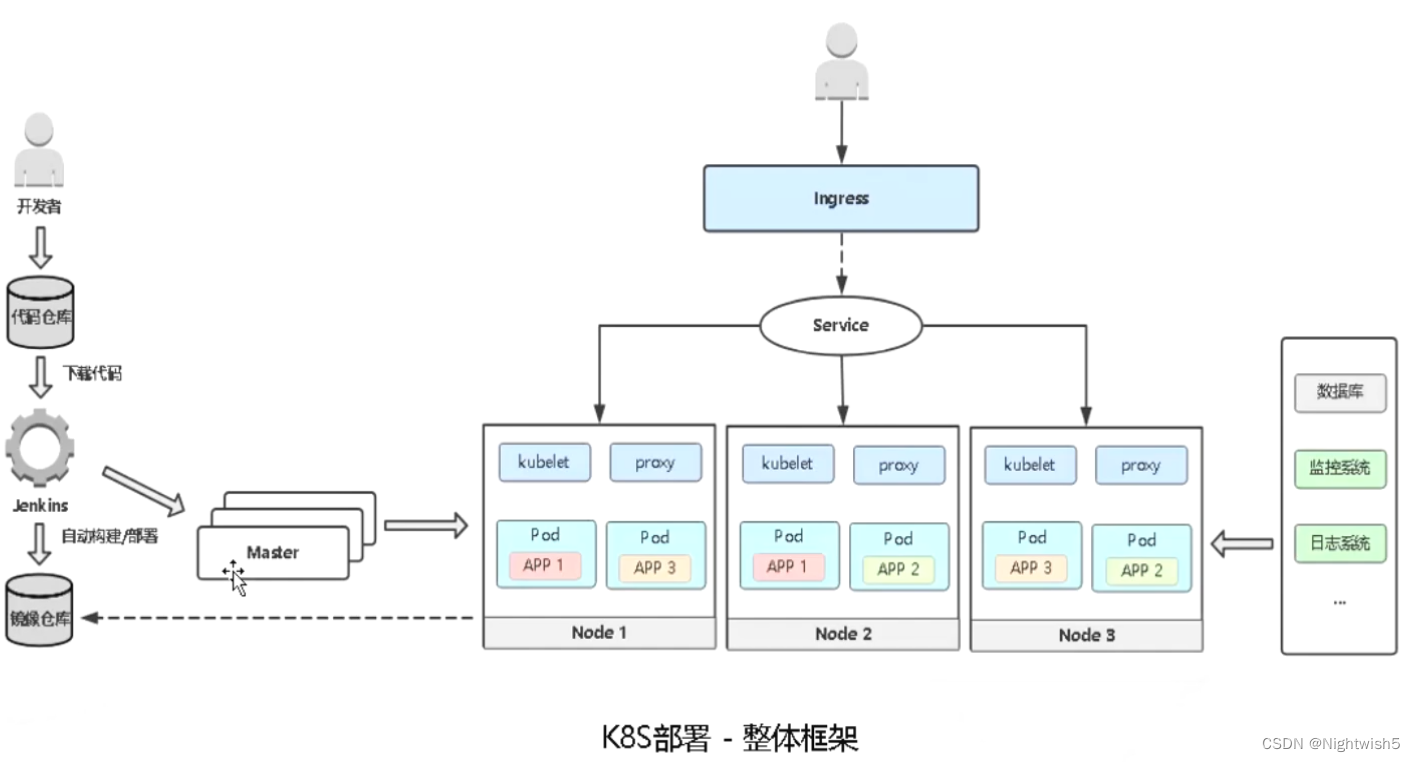
从运维角度看微服务 k8s部署微服务【偏理论】【AL】
从运维角度看微服务 & 部署微服务【偏理论】 1、微服务的特点 服务组件化: 每个服务独立开发、部署,有效避免一个服务的修改引起整个系统重新部署。 技术栈灵活: 约定通信方式,使得服务本身功能实现对技术要求不再那么敏感。…...
专题 | 防抖和节流
一 防抖:单位时间内,频繁触发事件,只执行最后一次 场景:搜索框搜索输入(利用定时器,每次触发先清掉以前的定时器,从新开始) 节流:单位时间内,频繁触发事件&…...

C++入门:重载运算符和重载函数
C 允许在同一作用域中的某个函数和运算符指定多个定义,分别称为函数重载和运算符重载。重载声明是指一个与之前已经在该作用域内声明过的函数或方法具有相同名称的声明,但是它们的参数列表和定义(实现)不相同。当您调用一个重载函…...

conda 新建虚拟环境 等等
1:conda create -n env_name package_name #创建名为env_name的新环境,并在该环境下安装名为package_name 的包,例如:conda create -n Arg python3.8 # 创建名字为Arg python为3.8版本的虚拟环境2: conda activate env…...
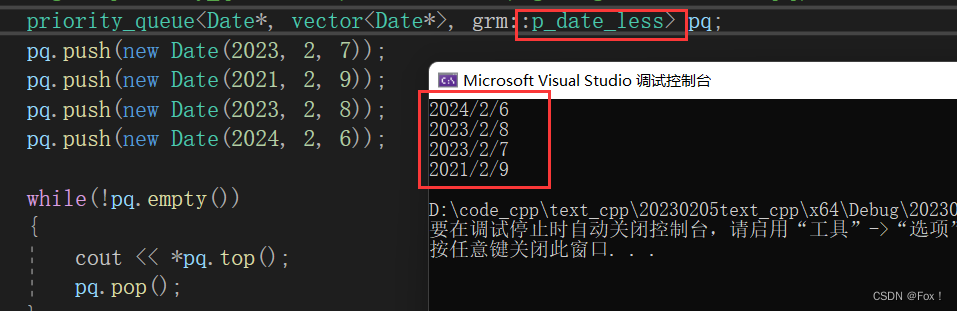
【C++:STL之栈和队列 | 模拟实现 | 优先级队列 】
目录 1. stack的介绍和使用 1.1 stack的介绍 1.2 stack的使用 2 栈的模拟实现 3 queue的介绍和使用 3.1 queue的介绍 3.2 queue的使用 4 queue的模拟实现 5 deque的介绍 5.1deque的原理介绍 5.2 deque的缺陷 5.3 为什么选择deque作为stack和queue的底层默认容器 6 p…...
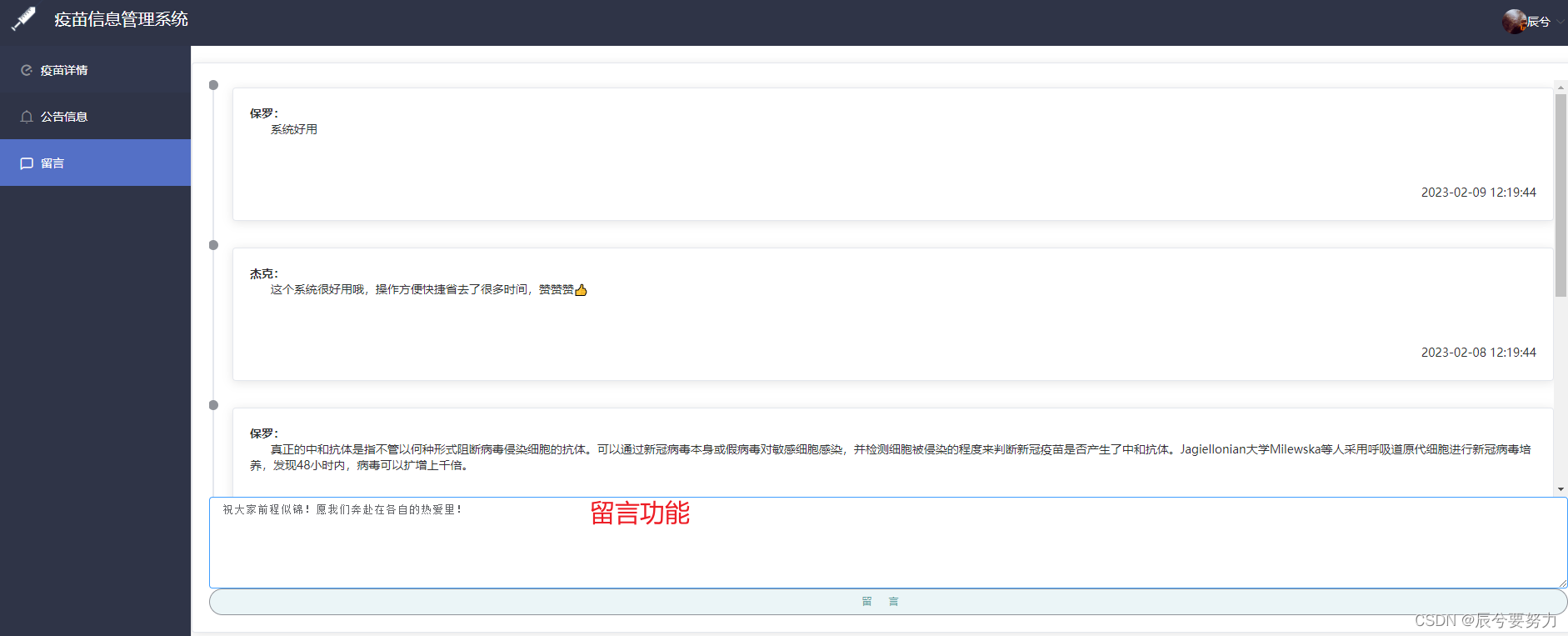
基于SpringBoot+Vue的疫苗预约管理系统(Java项目)
【辰兮要努力】:hello你好我是辰兮,很高兴你能来阅读,昵称是希望自己能不断精进,向着优秀程序员前行! 博客来源于项目以及编程中遇到的问题总结,偶尔会有读书分享,我会陆续更新Java前端、后台、…...
,真题含思路)
华为OD机试 - 计算网络信号(Python),真题含思路
计算网络信号 题目 网络信号经过传递会逐层衰减,且遇到阻隔物无法直接穿透,在此情况下需要计算某个位置的网络信号值。 注意:网络信号可以绕过阻隔物 array[m][n] 的二维数组代表网格地图,array[i][j] = 0 代表 i 行 j 列是空旷位置;array[i][j] = x ( x 为正整数)代表 i …...

【Spring】注解实现IOC操作,你理解了吗?
作者:狮子也疯狂 专栏:《spring开发》 坚持做好每一步,幸运之神自然会驾凌在你的身上 专栏推荐:写文章刚刚起步,各个专栏的知识点后续会补充完善,不断更新好文,希望大 家支持一下。 专栏名字El…...

微搭低代码从入门到精通01-总体介绍
在过去我们开发小程序,要学习各类知识。比如前端知识、后端知识、服务器知识及各种中间件及数据库的知识。 要想学会这些知识,既需要投入大量的学习时间,而且要经过相当的实践才可以掌握。 如果立志从事开发行业,投入精力去学习…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

数据库——redis
一、Redis 介绍 1. 概述 Redis(Remote Dictionary Server)是一个开源的、高性能的内存键值数据库系统,具有以下核心特点: 内存存储架构:数据主要存储在内存中,提供微秒级的读写响应 多数据结构支持&…...

boost::filesystem::path文件路径使用详解和示例
boost::filesystem::path 是 Boost 库中用于跨平台操作文件路径的类,封装了路径的拼接、分割、提取、判断等常用功能。下面是对它的使用详解,包括常用接口与完整示例。 1. 引入头文件与命名空间 #include <boost/filesystem.hpp> namespace fs b…...

结构化文件管理实战:实现目录自动创建与归类
手动操作容易因疲劳或疏忽导致命名错误、路径混乱等问题,进而引发后续程序异常。使用工具进行标准化操作,能有效降低出错概率。 需要快速整理大量文件的技术用户而言,这款工具提供了一种轻便高效的解决方案。程序体积仅有 156KB,…...
