信息与未来2015真题笔记
[信息与未来 2015] 加数
题目描述
给出一个正整数 n n n,在 n n n 的右边加入 ⌊ n 2 ⌋ \left\lfloor\dfrac n2\right\rfloor ⌊2n⌋,然后在新数的右边
再加入 ⌊ ⌊ n 2 ⌋ 2 ⌋ \left\lfloor\dfrac{\left\lfloor\dfrac n2\right\rfloor}2\right\rfloor 2⌊2n⌋ ,一直这样进行下去,直到加入的数为 0 0 0 为止(注意, 0 0 0 不应当被加入)。
求加数结束后新数的长度。
输入格式
一行一个整数 n n n。
输出格式
一行一个整数,为加数结束后新数的长度。
样例 #1
样例输入 #1
37
样例输出 #1
8
提示
样例解释
- ⌊ 37 2 ⌋ = 18 \left\lfloor\dfrac{37}2\right\rfloor=18 ⌊237⌋=18,加到 n n n 的右边成为 3718 3718 3718;
- ⌊ 18 2 ⌋ = 9 \left\lfloor\dfrac{18}2\right\rfloor=9 ⌊218⌋=9,加到新数的右边成为 37189 37189 37189;
- ⌊ 9 2 ⌋ = 4 \left\lfloor\dfrac{9}2\right\rfloor=4 ⌊29⌋=4,加到新数的右边成为 371894 371894 371894;
- ⌊ 4 2 ⌋ = 2 \left\lfloor\dfrac{4}2\right\rfloor=2 ⌊24⌋=2,加到新数的右边成为 3718942 3718942 3718942;
- ⌊ 2 2 ⌋ = 1 \left\lfloor\dfrac{2}2\right\rfloor=1 ⌊22⌋=1,加到新数的右边成为 37189421 37189421 37189421;
- ⌊ 1 2 ⌋ = 0 \left\lfloor\dfrac12\right\rfloor=0 ⌊21⌋=0,加数结束,最后得到的数是一个 8 8 8 位数。
数据范围
1 ≤ n ≤ 1 0 5 1\le n\le10^5 1≤n≤105。
思路
直接模拟,判断位数。
代码
#include <bits/stdc++.h>
//#define int long long
using namespace std;int n;
int sum;void solve()
{cin >> n;while (n){int m = n,num = 0;while (m)m /= 10,num++;sum += num;n /= 2;}cout << sum;
}signed main()
{solve();return 0;
}
[信息与未来 2015] 中间值
题目描述
给出一个正整数 n n n,生成长度为 n n n 的数列 a a a,其中 a i = i ( 1 ≤ i ≤ n ) a_i=i(1\le i\le n) ai=i(1≤i≤n)。
- 若 n n n 为奇数,则输出 a a a 的中间数(位于 a a a 正中位置的数);
- 若 n n n 为偶数,则输出位于 a a a 中间两个数的和。
输入格式
一个正整数 n n n。
输出格式
一个正整数。若 n n n 为奇数,则输出其中间值;若 n n n 为偶数,则输出两个中间值的和。
样例 #1
样例输入 #1
9
样例输出 #1
5
样例 #2
样例输入 #2
10
样例输出 #2
11
提示
1 ≤ n ≤ 1 0 18 1\le n\le10^{18} 1≤n≤1018。
思路
若 n n n 为奇数,则答案为 n ÷ 2 + 1 n\div2+1 n÷2+1;
若 n n n 为偶数,则答案为 n + 1 n+1 n+1。
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;int n;void solve()
{cin >> n;if (n % 2)cout << n/2+1;elsecout << n+1;
}signed main()
{solve();return 0;
}
[信息与未来 2015] 买木头
题目描述
有 n n n 个木材供应商,每个供应商有长度相同的一定数量的木头。长木头可以锯短,但短木头不能接长。有一个客人要求 m m m 根长度相同的木头,要求计算出:此时供货商提供的木头满足客人要求的最大长度是多少。
例如 n = 2 , m = 30 n=2,m=30 n=2,m=30,两个供货商的木头为:
- 12 , 10 12,10 12,10(第 1 1 1 个供货商的木头长度为 12 12 12,共有 10 10 10 根);
- 5 , 10 5,10 5,10(第 2 2 2 个供货商的木头长度为 5 5 5,共有 10 10 10 根)。
计算的结果为 5 5 5,即长度为 12 12 12 的木头一根可锯出两根长度为 5 5 5 的木头,多余的无用;长度为 5 5 5 的木头不动,此时,可以得到 30 30 30 根长度为 5 5 5 的木头。
输入格式
一行四个整数 n , m , l 1 , s 1 n,m,l_1,s_1 n,m,l1,s1。其中 l 1 l_1 l1 是第一个供货商木头的长度, s 1 s_1 s1 是第一个供货商木头的数量。其他供货商木头
的长度和数量 l i l_i li 和 s i ( i ≥ 2 ) s_i(i\ge2) si(i≥2)由下面的公式给出:
- l i = ( ( l i − 1 × 37011 + 10193 ) m o d 10000 ) + 1 l_i=((l_{i-1}\times37011+10193) \bmod 10000)+1 li=((li−1×37011+10193)mod10000)+1;
- s i = ( ( s i − 1 × 73011 + 24793 ) m o d 100 ) + 1 s_i=((s_{i-1}\times73011+24793) \bmod 100)+1 si=((si−1×73011+24793)mod100)+1。
输出格式
一个整数,即满足要求的 m m m 根长度相同的木头的最大长度。
样例 #1
样例输入 #1
10 10000 8 20
样例输出 #1
201
提示
1 ≤ n ≤ 1 0 4 , 1 ≤ m ≤ 1 0 6 , 1 ≤ l 1 ≤ 1 0 4 , 1 ≤ s 1 ≤ 100 1\le n\le10^4,1\le m\le10^6,1\le l_1\le10^4, 1\le s_1\le100 1≤n≤104,1≤m≤106,1≤l1≤104,1≤s1≤100。
思路
二分木头的长度,每次 check 判断数量是否足够。
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;int n,m;
int a[10010],b[10010];bool judge(int x)
{int sum = 0;for (int i = 1;i <= n;i++)sum += a[i]/x*b[i];return sum >= m;
}void solve()
{cin >> n >> m >> a[1] >> b[1];for (int i = 2;i <= n;i++)a[i] = ((a[i-1]*37011+10193)%10000) + 1;for (int i = 2;i <= n;i++)b[i] = ((b[i-1]*73011+24793)%100) + 1;int l = 1,r = 10000,best;while (l <= r){int mid = (l+r)/2;if (judge(mid))best = mid,l = mid+1;elser = mid-1;}cout << best;
}signed main()
{solve();return 0;
}
[信息与未来 2015] 拴奶牛
题目描述
有 n n n 头奶牛,有 k k k 个木桩,每个木桩有一个位置,一个木桩上只能拴一头奶牛。由于奶牛好斗,所以在拴奶牛的时候,要求距离最近的奶牛的距离尽可能大。
例如 n = 4 , k = 6 n=4,k=6 n=4,k=6,木桩的位置为 0 , 3 , 4 , 7 , 8 , 9 0,3,4,7,8,9 0,3,4,7,8,9,此时为下图。
KaTeX parse error: Unexpected end of input in a macro argument, expected '}' at position 12: \underline\̲t̲e̲x̲t̲{\qquad O\quad …
有许多种拴牛方案,例如:
- 0 , 3 , 4 , 9 0,3,4,9 0,3,4,9:此时最近距离为 1 1 1( 3 , 4 3,4 3,4 之间);
- 0 , 3 , 7 , 9 0,3,7,9 0,3,7,9:此时最近距离为 2 2 2。
输入格式
三个整数 n , k , p 1 n,k,p_1 n,k,p1,其中 p 1 p_1 p1 为第 1 1 1 个木桩的位置,其他木桩 p i ( i ≥ 2 ) p_i(i\ge2) pi(i≥2) 的位置由下面公式给出:
p i = p i − 1 + ( ( p i − 1 × 2357 + 137 ) m o d 10 ) + 1 p_i = p_{i-1} + ((p_{i-1}\times2357+137) \bmod 10)+1 pi=pi−1+((pi−1×2357+137)mod10)+1。
输出格式
一个整数,即奶牛间最近距离的最大值。
样例 #1
样例输入 #1
25 70 99
样例输出 #1
12
提示
1 ≤ n ≤ k ≤ 1 0 6 , 0 ≤ p 1 ≤ 100 1\le n\le k\le10^6,0\le p_1\le100 1≤n≤k≤106,0≤p1≤100。
思路
二分两只牛之间的距离,每次 check 判断木桩是否足够。
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;int n,m;
int a[1000010];bool judge(int x)
{int last = 1,num = 1;for (int i = 2;i <= m;i++)if (a[i]-a[last] >= x)num++,last = i;return num >= n;
}void solve()
{cin >> n >> m >> a[1];for (int i = 2;i <= m;i++)a[i] = a[i-1] + ((a[i-1]*2357+137) % 10) + 1;int l = 1,r = 1e9,best;while (l <= r){int mid = (l+r)/2;if (judge(mid))best = mid,l = mid+1;elser = mid-1;}cout << best;
}signed main()
{solve();return 0;
}
[信息与未来 2015] 分数计数
题目描述
有 n n n 个球队,编号为 1 ∼ n 1\sim n 1∼n,共进行 n n n 场比赛,每场比赛有一个胜队。计分方法如下:
- 是连胜中的第一次胜利,则本次胜利得 1 1 1 分。
- 是连胜中的第二次胜利,则本次胜利得 2 2 2 分。
- 是连胜中的第三次胜利,则本次胜利得 3 3 3 分。
- 连胜超过三次以上的胜场,每场得 3 3 3 分。
例如 n = 12 n=12 n=12,比赛的胜队为 1 , 2 , 1 , 1 , 3 , 2 , 1 , 1 , 1 , 1 , 4 , 2 1,2,1,1,3,2,1,1,1,1,4,2 1,2,1,1,3,2,1,1,1,1,4,2,计分如下:
- 队 1 1 1: 1 + 1 + 2 + 1 + 2 + 3 + 3 = 13 1+1+2+1+2+3+3=13 1+1+2+1+2+3+3=13 分;
- 队 2 2 2: 1 + 1 + 1 = 3 1+1+1=3 1+1+1=3 分;
- 队 3 ∼ 4 3\sim 4 3∼4: 1 1 1 分。
- 队 5 ∼ 12 5\sim 12 5∼12: 0 0 0 分。
求得分最多的队伍的分数。
输入格式
两个整数 n , x 1 n,x_1 n,x1, n n n 为球队数, x 1 x_1 x1 为第一次胜队号,第 i ( i ≥ 2 ) i(i\ge2) i(i≥2) 场比赛胜队的编号由
以下公式确定:
x i = ( ( x i − 1 × 3703 + 1047 ) m o d n ) + 1 x_i = ((x_{i-1}\times 3703+1047) \bmod n)+1 xi=((xi−1×3703+1047)modn)+1。
输出格式
一个整数,即得分最多队的分数。
样例 #1
样例输入 #1
10 5
样例输出 #1
3
提示
1 ≤ x 1 ≤ n ≤ 1 0 6 1\le x_1\le n\le10^6 1≤x1≤n≤106。
思路
按照题目要求模拟。
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;int n;
int a[1000010],sum[1000010];void solve()
{cin >> n >> a[1];for (int i = 2;i <= n;i++)a[i] = ((a[i-1]*3703+1047)%n) + 1;int now = 0;for (int i = 1;i <= n;i++){if (a[i] == a[i-1])now++;elsenow = 1;if (now >= 3)sum[a[i]] += 3;elsesum[a[i]] += now;}int mx = 0;for (int i = 1;i <= n;i++)mx = max(mx,sum[i]);cout << mx;
}signed main()
{solve();return 0;
}
[信息与未来 2015] 求回文数
题目描述
一个正整数,正读和反读都相同的数为回文数,例如 22 , 131 , 2442 , 37073 , 6 , ⋯ 22,131,2442,37073,6,\cdots 22,131,2442,37073,6,⋯。所有的 1 1 1 位数都是回文数。
现给出一个正整数 n n n,求出 [ 1 , n ] [1,n] [1,n] 中的回文数的个数。
输入格式
一个整数 n n n。
输出格式
一个整数,即 1 ∼ n 1\sim n 1∼n 中全部回文数的个数。
样例 #1
样例输入 #1
24
样例输出 #1
11
提示
样例解释
在 1 1 1 至 24 24 24 中,回文数有 1 ∼ 9 , 11 , 22 1\sim 9,11,22 1∼9,11,22,共 11 11 11 个。
数据范围
1 ≤ n ≤ 1 0 4 1\le n\le10^4 1≤n≤104。
思路
枚举。从 1 1 1 枚举到 n n n,然后判断是否为回文数。
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;int n;
int sum;bool judge(int x)
{int y = x,numa = 0;while (y)numa = numa*10+y%10,y /= 10;if (numa == x)return true;return false;
}void solve()
{cin >> n;for (int i = 1;i <= n;i++)if (judge(i))sum++;cout << sum;
}signed main()
{solve();return 0;
}
[信息与未来 2015] 连续数的和
题目描述
给出两个整数 n n n 和 k k k,求出 1 ∼ n 1\sim n 1∼n 中连续 k k k 个数的和为完全平方数的个数。
输入格式
一行两个整数 n , k n,k n,k。
输出格式
一行一个整数,即 1 ∼ n 1\sim n 1∼n 中连续 k k k 个数的和为平方数的个数。
样例 #1
样例输入 #1
10 3
样例输出 #1
1
提示
样例解释
在 1 ∼ 10 1\sim10 1∼10 中,连续 3 3 3 个数的和有:
- 1 + 2 + 3 = 6 1+2+3=6 1+2+3=6;
- 2 + 3 + 4 = 9 = 3 2 2+3+4=9=3^2 2+3+4=9=32;
- 3 + 4 + 5 = 12 3+4+5=12 3+4+5=12;
- 4 + 5 + 6 = 15 4+5+6=15 4+5+6=15;
- 5 + 6 + 7 = 18 5+6+7=18 5+6+7=18;
- 6 + 7 + 8 = 21 6+7+8=21 6+7+8=21;
- 7 + 8 + 9 = 24 7+8+9=24 7+8+9=24;
- 8 + 9 + 10 = 27 8+9+10=27 8+9+10=27。
故只有 1 1 1 个。
数据范围
2 ≤ n ≤ 7 × 1 0 4 , 1 ≤ k ≤ n 2\le n\le 7\times 10^4,1\le k\le n 2≤n≤7×104,1≤k≤n。
思路
枚举所有情况,判断是否为平方数。
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;void solve()
{int n,k;cin >> n >> k;int now = (1+k)*k/2,sum = 0;for (int i = k;i <= n;i++){if ((int)(sqrt(now))*(int)(sqrt(now)) == now)sum++;now -= (i-k+1);now += i+1;}cout << sum;
}signed main()
{solve();return 0;
}
[信息与未来 2015] 夏令营小旗手
题目描述
2015 2015 2015 年江苏省“信息与未来”小学夏令营在洪泽县实验小学进行,组委会决定在洪泽实验小学的学生中挑选一名小旗手,推选方法如下:
洪泽实验小学有 n n n 名学生,每名学生有一个学号,学号为 1 ∼ n 1\sim n 1∼n。同时,每名同学有一张选票,可以推选一名同学为小旗手,最后,得票最多者当选;若得票最有多名(票数相同),则学号小者当选。
例如 n = 8 n=8 n=8,选票为 2 , 3 , 4 , 4 , 3 , 4 , 1 , 6 2,3,4,4,3,4,1,6 2,3,4,4,3,4,1,6, 4 4 4 号学生得票最多( 3 3 3 票),当选小旗手。
输入格式
两个整数 n , x 1 n,x_1 n,x1, n n n 为学生数, x 1 x_1 x1 为第一个选票上的学号,之后的选票 x i ( i ≥ 2 ) x_i(i\ge2) xi(i≥2) 由下面的递推关系给出:
x i = ( ( x i − 1 × 37 + 33031 ) m o d n ) + 1 x_i = ((x_{i-1}\times 37+33031)\bmod n)+1 xi=((xi−1×37+33031)modn)+1。
其中 m o d \bmod mod 为取余运算。例如, 13 m o d 8 = 5 , 21 m o d 21 = 0 13 \bmod 8 = 5,21 \bmod 21 = 0 13mod8=5,21mod21=0。根据这个公式,就能从 x 1 x_1 x1 推出 x 2 ∼ n x_{2\sim n} x2∼n。
输出格式
一个整数,即选出的小旗手的学号。
样例 #1
样例输入 #1
5 2
样例输出 #1
2
提示
样例解释
x = { 2 , 1 , 4 , 5 , 2 } x=\{2,1,4,5,2\} x={2,1,4,5,2}, 2 2 2 号选手票数最多。
数据范围
1 ≤ x 1 ≤ n ≤ 1 0 3 1\le x_1\le n\le10^3 1≤x1≤n≤103。
思路
先算出每个人的投票,然后用 vis 记录求出最大值。
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;int vis[1010];void solve()
{int n,m;cin >> n >> m;vis[m]++;for (int i = 2;i <= n;i++){m = ((m*37 + 33031)%n) + 1;vis[m]++;}int mx = 0,pos = 0;for (int i = 1;i <= n;i++)if (mx < vis[i]){mx = vis[i];pos = i;}cout << pos;
}signed main()
{solve();return 0;
}
相关文章:

信息与未来2015真题笔记
[信息与未来 2015] 加数 题目描述 给出一个正整数 n n n,在 n n n 的右边加入 ⌊ n 2 ⌋ \left\lfloor\dfrac n2\right\rfloor ⌊2n⌋,然后在新数的右边 再加入 ⌊ ⌊ n 2 ⌋ 2 ⌋ \left\lfloor\dfrac{\left\lfloor\dfrac n2\right\rfloor}2\rig…...

【成功解决】Access token invalid or no longer valid
项目场景: python调用文心一言对应的ERNIE-4.0-8K模型API接口,方式为单次调用 问题描述 提示: “error_code”: 110, “error_msg”: “Access token invalid or no longer valid” C:\Users\PUB\AppData\Local\Programs\Python\Python38-…...

【Bug】修改计算机名称出现ip无法连接mysql数据库
解决: mysql -u root -p输入密码登录mysql服务器,那个ip是本机ip4的地址单ip放行。推荐全部,后面123456是密码 GRANT ALL PRIVILEGES ON *.* TO root192.168.0.109 IDENTIFIED BY 123456; 全部IP都放行 GRANT ALL PRIVILEGES ON *.* …...

米尔MYC-Y6ULX-V2开发板测评记录
文章目录 1、板子上手体验2、板载硬件3、系统信息4、 驱动测试5、编译linux三大件7、摄像头测试9、总结 1、板子上手体验 首先非常感谢芯查查给了这样一个机会来测评这样一款性能十分强大的开发板,我拿到手的是MYC-Y6ULX-V2核心板及开发板,这块板子具有…...

装修全流程
Summary 从2023年底到现在(2024年6月2日),装修可以定的东西基本过半了,我按照时间顺序把每个环节的内容和想法都记录一下 环节 选装修公司、找设计师设计环节预算计算角色介绍建材选型敲墙和开工水电放样泥工木工放样To be cont…...
探索微软Edge
微软开发的官方浏览器 Microsoft Edge是微软基于 Chromium 开源项目及其他开源软件开发的网页浏览器。 2015年4月30日,微软在旧金山举行的Build 2015开发者大会上宣布——Windows 10内置代号为“Project Spartan”的新浏览器被正式命名为“Microsoft Edge”&#x…...

Java面试——专业技能
优质博文:IT-BLOG-CN 一、简单讲下 Java 的跨平台原理 由于各个操作系统(Windows,Linux等)支持的指令集不是完全一致的。就会让我们程序在不同的操作系统上要执行不同的程序代码。Java 开发了适用于不同操作系统及位数的 Java 虚拟…...

C#按钮样式设置XMAL
统一按钮样式 <Window.Resources> <!--按钮样式统一设置,个别按钮单独定义样式的话则需要在定义按钮位置单独设置--><Style TargetType"Button"><Setter Property"Background" Value"Red"/><Setter Prop…...

EmmyLua注释详解
Lua EmmyLua 注解详解 Why 为了使 IDE 编码体验和强语言相近 让 IDE 提前发现编码错误 BUG 查找更方便 代码阅读更方便 建议 明确字段类型 明确字段访问修饰符 明确方法参数类型 善用 “:” 继承 “|” 或 ","多个 支持格式 –类 —class MY_TYPE[:PARENT_TYPE] [com…...

Linux内核 -- 启用 Linux 内核调试信息
启用 Linux 内核调试信息 本文档提供了如何在编译 Linux 内核时启用调试信息的逐步指南。调试信息对于调试和诊断内核问题至关重要。 启用调试信息的步骤 1. 进入内核源代码目录 打开终端并导航到 Linux 内核源代码目录: cd /path/to/linux-kernel2. 配置内核 …...
vs2019 无法打开QT的UI文件
/* * --------------------------- Microsoft Visual StudioQt5.15.2\5.15.2\msvc2019_64 --------------------------- D:\QT_Project_vs\QtWidgetsApplication1\QtWidgetsApplication1\QtWidgetsApplication1.ui 无法打开文件。 --------------------------- 确定 -------…...

Python | A + B问题|||
if语句:if、elif、else 关系运算符 逻辑运算符:and(&&)、or(||)、not(!) break退出循环 continue:只能出现在for、while循环内部,用法…...
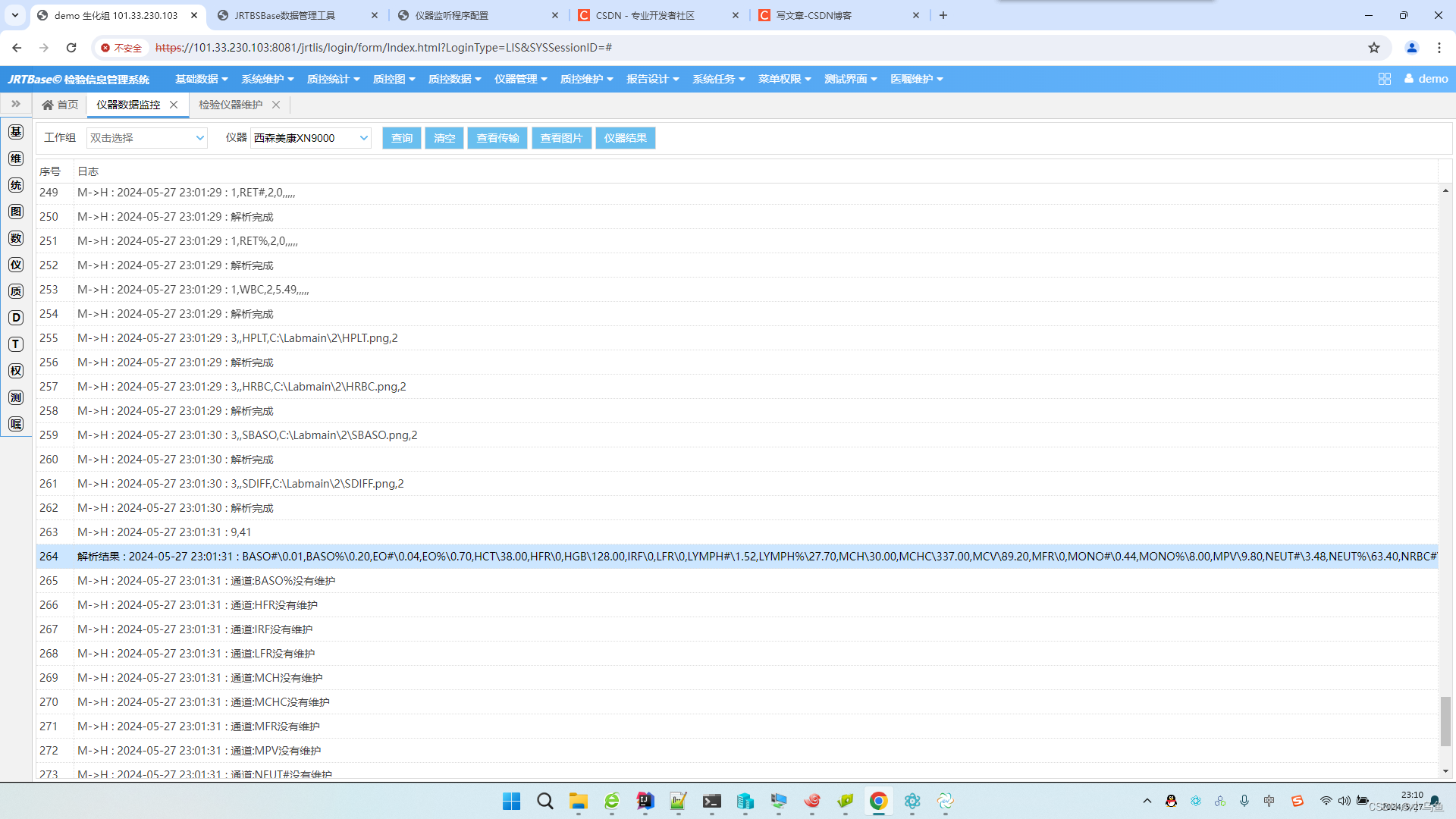
JRT连接希森美康出图
良好的设计源自实践,优秀的基础决定上限 上一篇用JRT连设备实现了比较有难度的Sebia绘图设备和TCP模式连接。这次连接最常见的检验设备(西森美康),读文件和图上传出图。 视频演示 结果格式 通道对应 接口设置 接口处理实现…...

UVa11604 General Sultan
UVa11604 General Sultan 题目链接题意分析AC 代码 题目链接 UVA - 11604 General Sultan 题意 给出一些0和1组成的模式串,问是否存在一个串使得有多种方案将这个串分解成模式串。 给一个包含n(n≤100)个符号的二进制编码方式ÿ…...

USB - ACK、NAK和STALL的含义
在 USB(通用串行总线)通信中,术语 ACK、NAK 和 STALL 指的是用于控制数据流和错误处理的握手数据包。下面是对每个术语的详细解释: ACK(确认): ACK 数据包由接收方发送给发送方,以表…...
 IP 地址)
查看 WSL2 (Windows Subsystem for Linux 2) IP 地址
查看 WSL2 [Windows Subsystem for Linux 2] IP 地址 1. ipconfig2. ping $(hostname).local3. cat /etc/resolv.conf4. ip route show5. ip addrReferences 1. ipconfig Windows 系统上与 WSL2 (Windows Subsystem for Linux 2) 接口的地址 172.31.32.1。 Microsoft Windows…...

如何判断一个JavaScript对象是否为空?
在JavaScript的世界里,"空对象"这一术语的含义在不断演变。随着ECMA Script的更新和改进,判断一个对象是否为空变得更加复杂。本文将详细介绍如何判断一个JavaScript对象是否为空,并讨论各种解决方案的优缺点。 历史背景 在理解如何判断一个对象是否为空之前,我…...

小白跟做江科大32单片机之LED闪烁
原理介绍 原理介绍详见: 【STM32】江科大STM32学习笔记汇总(已完结)_stm32江科大笔记-CSDN博客https://blog.csdn.net/u010249597/article/details/134762513 项目准备 1.在项目文件夹中新建3-1 LED文件夹 2.keil新建项目,打开新建的3-1 LED…...

“世界酒中国菜”系列活动如何助推乡村振兴和文化交流?
"世界酒中国菜"系列活动如何助推乡村振兴和文化交流? 《经济参考报》(2024年5月24日 第6版) 新华社北京(记者 张晓明) “世界酒中国菜”系列活动自启动以来,已在国内外产生了广泛影响。这一国家…...
上位机图像处理和嵌入式模块部署(f407 mcu中fatfs中间件使用)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 前面我们已经实现了spi norflash的驱动,理论上这已经可以实现数据的持久化保存了。为什么还需要一个文件系统呢?主要原因还…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...
