当前位置： 首页 > news >正文

spring项目修改时间格式

news 2026/2/8 20:00:03

一、配置方式

在application.yml上添加

spring:jackson:date-format: yyyy-MM-dd HH:mm:sstime-zone: GMT+8

二、注解方式

1、添加依赖

        <dependency><groupId>com.fasterxml.jackson.core</groupId><artifactId>jackson-annotations</artifactId><version>2.9.6</version></dependency>

2、配置注解

    @JsonFormat(pattern = "yyyy-MM-dd HH:mm:ss",timezone = "GMT+8")private Date createTime;
  1. 在属性上加上 @JsonFormat 注解；
  2. 参数 pattern：需要转换的日期格式，当然也可以“yyyy-MM-dd HH:mm:ss”；
  3. 参数 timezone：@JsonFormat注解使用的是标准的GMT时间，于北京时间差8小时，所以需要“GMT+8” 来达到北京时间同步； 
  4. 时区(GMT)简介：格林尼治标准时间（旧译格林威治平均时间或格林威治标准时间；英语：GreenwichMeanTime，GMT）是指位于英国伦敦郊区的皇家格林尼治天文台的标准时间，也是目前的协调世界时（UTC），与北京时间慢8个小时，所以需要(GMT+8)。

相关文章：

spring项目修改时间格式

一、配置方式 在application.yml上添加 spring:jackson:date-format: yyyy-MM-dd HH:mm:sstime-zone: GMT8 二、注解方式 1、添加依赖 <dependency><groupId>com.fasterxml.jackson.core</groupId><artifactId>jackson-annotations</artifactId&…...

编程日记 2024/6/3 4:19:33

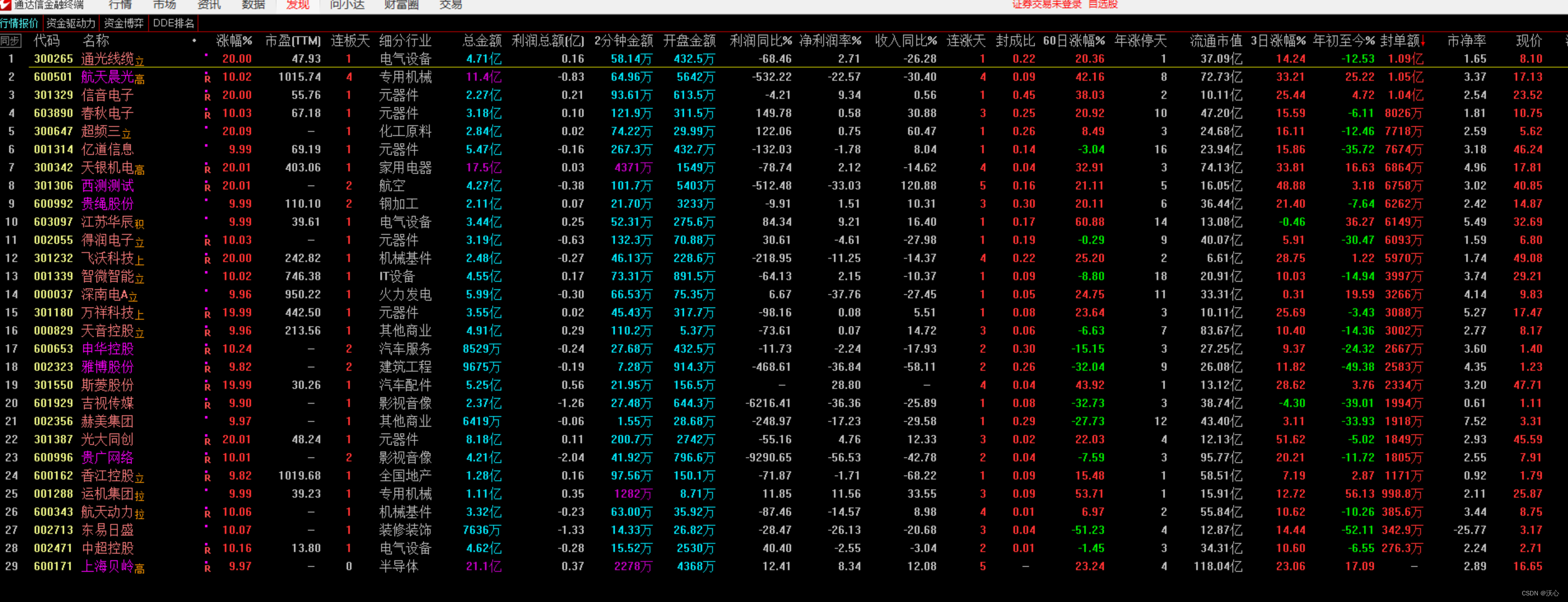
每周统计-20240531

用于测试程序的稳定性&#xff1a; 龙虎榜&#xff1a; 成交额&#xff1a; 封成比&#xff1a; 收盘前放量&#xff1a; 开盘抢筹&#xff1a; 封单额&#xff1a;...

编程日记 2024/6/3 4:18:31

【工具】探索 DOU：每用户数据使用量

缘分让我们相遇乱世以外 命运却要我们危难中相爱 也许未来遥远在光年之外 我愿守候未知里为你等待 我没想到为了你我能疯狂到 山崩海啸没有你根本不想逃 我的大脑为了你已经疯狂到 脉搏心跳没有你根本不重要 &#x1f3b5; 邓紫棋《光年之外》 什么是 DOU…...

编程日记 2024/6/3 4:16:29

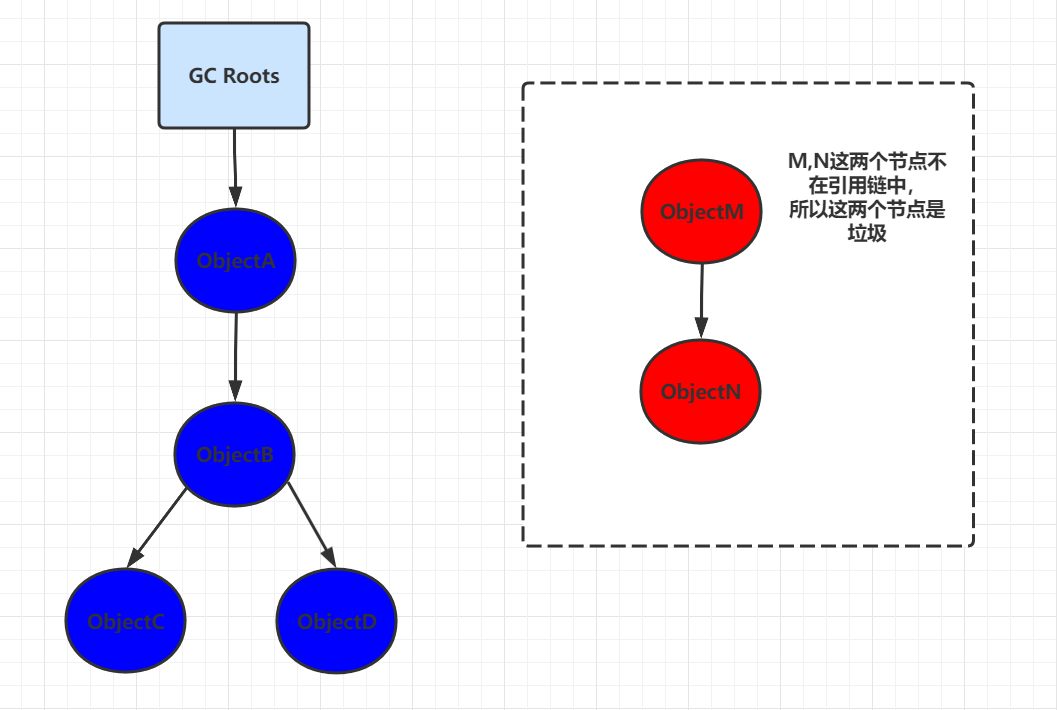
JVM之垃圾判断的详细解析

垃圾判断 垃圾介绍 垃圾&#xff1a;如果一个或多个对象没有任何的引用指向它了&#xff0c;那么这个对象现在就是垃圾 作用&#xff1a;释放没用的对象&#xff0c;清除内存里的记录碎片&#xff0c;碎片整理将所占用的堆内存移到堆的一端&#xff0c;以便 JVM 将整理出的内…...

编程日记 2024/6/3 4:13:26

07- Redis 中的 HyperLogLog 数据类型和应用场景

1. 介绍 Redis HyperLogLog 是 Redis 2.8.9 版本新增的数据类型&#xff0c;是一种用于【统计基数】的数据集合类型&#xff0c;基数统计就是指统计一个集合中不重复的元素个数。但要注意&#xff0c;HyperLogLog 的统计规则是基于概率完成的&#xff0c;不是非常准确&#xf…...

编程日记 2024/6/3 4:10:23

jenkins应用2-freestyle-job

1.jenkins应用 1.jenkins构建的流程 1.使用git参数化构建&#xff0c;用标签区分版本 2.git 拉取gitlab远程仓库代码 3.maven打包项目 4.sonarqube经行代码质量检测 5.自定义制作镜像发送到远程仓库harbor 6.在远程服务器上拉取代码启动容器 这个是构建的整个过程和步骤…...

编程日记 2024/6/3 4:09:21

K210视觉识别模块学习笔记1：第一个串口程序_程序烧录与开机启动

今日开始学习K210视觉识别模块:简单的认识与串口程序 亚博智能的K210视觉识别模块...... 固件库版本: canmv_yahboom_v2.1.1.bin 既然K210作为一个视觉识别外设模块来使用&#xff0c;我认为第一个程序 就没必要学点灯之类的了&#xff0c;直接学习串口如何配置开始为妥&…...

编程日记 2024/6/3 4:08:20

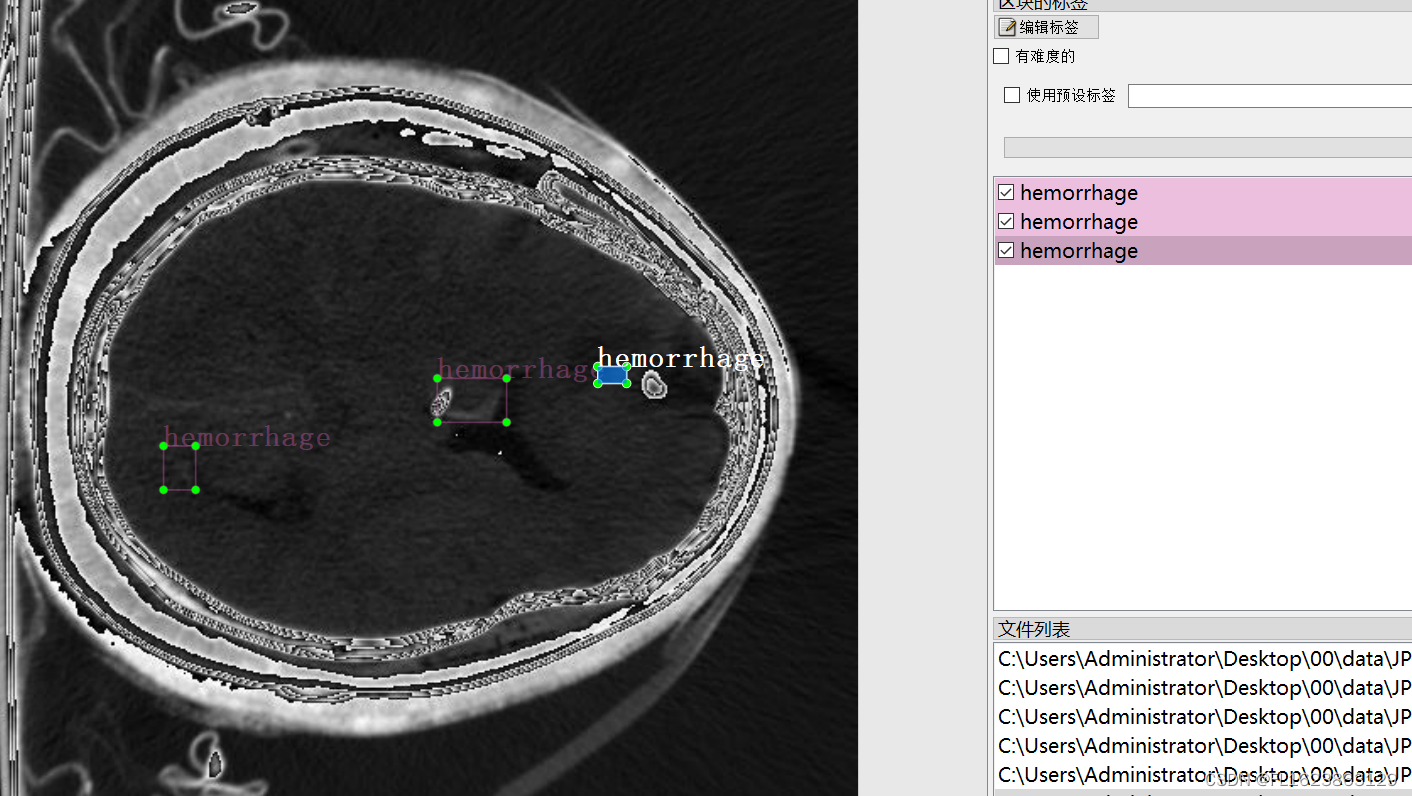
[数据集][目标检测]脑溢血检测数据集VOC+YOLO格式767张2类别

数据集格式&#xff1a;Pascal VOC格式YOLO格式(不包含分割路径的txt文件&#xff0c;仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数)&#xff1a;767 标注数量(xml文件个数)&#xff1a;767 标注数量(txt文件个数)&#xff1a;767 标注类别…...

编程日记 2024/6/3 4:06:17

如何借VR之手，让展厅互动更精彩？

VR虚拟现实技术以其卓越的沉浸式体验为特点&#xff0c;引领用户踏入一个全新的虚拟世界&#xff0c;正因如此&#xff0c;它开始被广泛应用于展厅、商业等多个领域。那么&#xff0c;今天&#xff0c;让我们就来了解一下这种技术是如何为展厅带来精彩互动体验的吧&#xff01;…...

编程日记 2024/6/3 4:05:16

微信小程序如何使用地图

微信小程序使用地图功能时&#xff0c;主要涉及到地图组件的引入、配置、以及相关的API调用。以下是一个详细的使用指南&#xff1a; 1. 引入地图组件 在微信小程序的.wxml文件中&#xff0c;通过<map>标签引入地图组件。你可以设置地图的经纬度、缩放级别、控件等属性…...

编程日记 2024/6/3 4:04:15

力扣 287. 寻找重复数

给定一个包含 n 1 个整数的数组 nums &#xff0c;其数字都在 [1, n] 范围内&#xff08;包括 1 和 n&#xff09;&#xff0c;可知至少存在一个重复的整数。假设 nums 只有 一个重复的整数 &#xff0c;返回 这个重复的数 。你设计的解决方案必须 不修改 数组 nums 且只用常量…...

编程日记 2024/6/3 4:03:14

怎样清理Mac存储空间 苹果电脑内存不够用怎么办 苹果电脑内存满了怎么清理

在使用 Mac 电脑的过程中&#xff0c;用户经常会遇到磁盘空间不足的困扰&#xff0c;这时候就需要寻找有效的方法来清理苹果电脑内存了。 清理Mac存储空间可以通过多种方法进行&#xff0c;以确保你的Mac能够高效运行并释放宝贵的存储空间。以下是一些有效的清理和优化方法&am…...

编程日记 2024/6/3 4:02:13

网络遗忘权的实现方法

网络遗忘权的实现方法 目录 从禁书说起 从销毁硬件信息的方法得到的启示 现在网络遗忘权的实现方法 从禁书说起 古代有禁书的需求,直接的方法就是贴出告示,强行收缴,然后付之一炬. 这个方法的问题在于只要有一个人敢冒死藏书,再次手抄或者是印刷,就 会让之前的禁书努力,付…...

编程日记 2024/6/3 4:00:10

【Python内功心法】：深挖内置函数，释放语言潜能

文章目录 &#x1f680;一、常见内置函数&#x1f308;二、高级内置函数⭐1. enumerate函数&#x1f44a;2. eval函数❤️3. exec函数&#x1f4a5;4. eval与exec 中 globals与locals如何用☔4-1 globals 参数&#x1f3ac;4-2 locals 参数 ❤️5. filter函数&#x1f44a;6. z…...

编程日记 2024/6/3 3:59:09

JS-09-es6常用知识1

目录 1 模板字符串 1.1 模板字符串基本用法 1.2 模板字符串解决了一些痛点 2 解构赋值 2.1 对象的解构赋值 2.2 函数参数的解构赋值 2.3 补写&#xff1a;属性的简写 3 rest参数 3.1 arguments 3.2 rest参数 3.3 补充&#xff1a;判断数据类型 4 箭头函数 4.1 …...

编程日记 2024/6/3 3:57:07

SpringBoot 基础之自动配置

SpringBoot 自动配置 SpringBoot 通过 自动配置 简化了大量的繁复的配置信息。 启动类 Application 中有两处特别之处&#xff1a; 注解&#xff1a;SpringBootApplication run 方法&#xff1a;SpringApplication.run(…) SpringBootApplication 注解至少等价于以下三个注…...

编程日记 2024/6/3 3:56:06

Oracle dblink 发现Network 等待事件的分析 enq: KO - fast object checkpoint

所有的sql 通过dblink 查询全部等待中&#xff0c; 同一个SQL 20多个session 在跑&#xff0c;等待事件network&#xff0c;可能怀疑是不是网络断开了&#xff0c;导致没有返回 执行sql 如下&#xff1a; BEGIN Xdblink ; END; 去到dblink 所在的db&#xff0c;发现20多个sql在…...

编程日记 2024/6/3 3:55:05

SpringMVC：向三大域对象存数据

1. 简介 Servlet中的三个域对象 请求域&#xff1a;request会话域&#xff1a;session应用域&#xff1a;application 主要是通过&#xff1a;setAttribute getAttribute方法来完成在域中数据的传递和共享。 点击跳转Servlet详细概念 // 向域中存储数据 void setAttribute(St…...

编程日记 2024/6/3 3:54:04

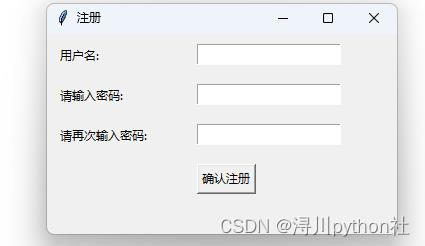
如何用python做一个用户登录界面——浔川python社

1 需解决的问题&#xff1a; 1.1如何用python做一个用户登录界面&#xff1f; 1.2需要用到哪些库、模块&#xff1f; 2 问题解决&#xff1a; 2.1 回答 1.1 &#xff1a;合理即可&#xff0c;无标准回答。 2.2 回答 1.2 &#xff1a;tk库&#xff08;缩写&#xff09;、GUL界面…...

编程日记 2024/6/3 3:52:01

Python知识点9---推导式

提前说一点&#xff1a;如果你是专注于Python开发&#xff0c;那么本系列知识点只是带你入个门再详细的开发点就要去看其他资料了&#xff0c;而如果你和作者一样只是操作其他技术的Python API那就足够了。 Python提供的推导式&#xff0c;只对列表、字典、集合三种数据类型生…...

编程日记 2024/6/3 3:51:00

【大模型RAG】Docker 一键部署 Milvus 完整攻略

本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装&#xff1b;只需暴露 19530&#xff08;gRPC&#xff09;与 9091&#xff08;HTTP/WebUI&#xff09;两个端口&#xff0c;即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

编程新知 2026/1/31 8:08:07

微信小程序 - 手机震动

一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注&#xff1a;文档 https://developers.weixin.qq…...

编程新知 2026/1/29 8:41:55

Android Bitmap治理全解析：从加载优化到泄漏防控的全生命周期管理

引言 Bitmap&#xff08;位图&#xff09;是Android应用内存占用的“头号杀手”。一张1080P&#xff08;1920x1080&#xff09;的图片以ARGB_8888格式加载时&#xff0c;内存占用高达8MB&#xff08;192010804字节&#xff09;。据统计&#xff0c;超过60%的应用OOM崩溃与Bitm…...

编程新知 2026/1/8 22:17:14

视觉slam十四讲实践部分记录——ch2、ch3

ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件，或者在构建过程中仍然引用了旧的路…...

编程新知 2026/2/6 15:56:54

springboot整合VUE之在线教育管理系统简介

可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生&#xff0c;小白用户&#xff0c;想学习知识的 有点基础&#xff0c;想要通过项…...

编程新知 2026/1/26 9:30:45

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf

FTP 客服管理系统 实现kefu123登录&#xff0c;不允许匿名访问&#xff0c;kefu只能访问/data/kefu目录&#xff0c;不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

编程新知 2026/1/25 9:03:19

RabbitMQ入门4.1.0版本（基于java、SpringBoot操作）

RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发&#xff0c;后来由Pivotal Software Inc.&#xff08;现为VMware子公司&#xff09;接管。RabbitMQ 是一个开源的消息代理和队列服务器&#xff0c;用 Erlang 语言编写。广泛应用于各种分布…...

编程新知 2026/1/31 3:52:49

力扣热题100 k个一组反转链表题解

题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

编程新知 2026/1/31 8:25:07

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing

Muffin 论文 现有方法 CRADLE 和 LEMON&#xff0c;依赖模型推理阶段输出进行差分测试&#xff0c;但在训练阶段是不可行的&#xff0c;因为训练阶段直到最后才有固定输出&#xff0c;中间过程是不断变化的。API 库覆盖低&#xff0c;因为各个 API 都是在各种具体场景下使用。…...

编程新知 2026/2/1 1:28:58

Vue3中的computer和watch

computed的写法 在页面中 <div>{{ calcNumber }}</div>script中 写法1 常用 import { computed, ref } from vue; let price ref(100);const priceAdd () > { //函数方法 price 1price.value ; }//计算属性 let calcNumber computed(() > {return ${p…...

编程新知 2025/11/8 20:34:42