堆排序-java
这次主要讲了堆排序和堆的基本构造,下一期会详细讲述堆的各种基本操作。
文章目录
前言
一、堆排序
1.题目描述
2.堆
二、算法思路
1.堆的存储
2. 结点下移down
3.结点上移up
4.堆的基本操作
5.堆的初始化
三、代码如下
1.代码如下:
2.读入数据:
3.代码运行结果
总结
前言
这次主要讲了堆排序和堆的基本构造,下一期会详细讲述堆的各种基本操作。
提示:以下是本篇文章正文内容,下面案例可供参考
一、堆排序
1.题目描述
输入一个长度为 n 的整数数列,从小到大输出前 m小的数。
输入格式
第一行包含整数 n 和 m。
第二行包含 n 个整数,表示整数数列。
输出格式
共一行,包含 m 个整数,表示整数数列中前 m 小的数。
数据范围
1≤m≤n≤100000,
1≤数列中元素≤1000000000
2.堆
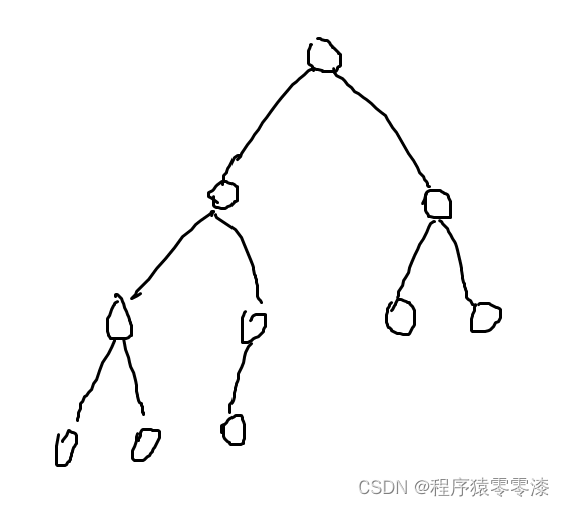
图2.1完全二叉树示意图
完全二叉树:一棵深度为k的有n个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编号,每一层最多有个结点,除了最后一层,其余层的结点数都是满的,且最后一层从左往右依次分布。
堆是一种基于完全二叉树的数据结构。可以分为大根堆,小根堆。
大根堆:每个结点的值都大于或者等于其左右孩子的值。
小根堆:每个结点的值都小于或者等于其左右孩子的值。
二、算法思路
1.堆的存储
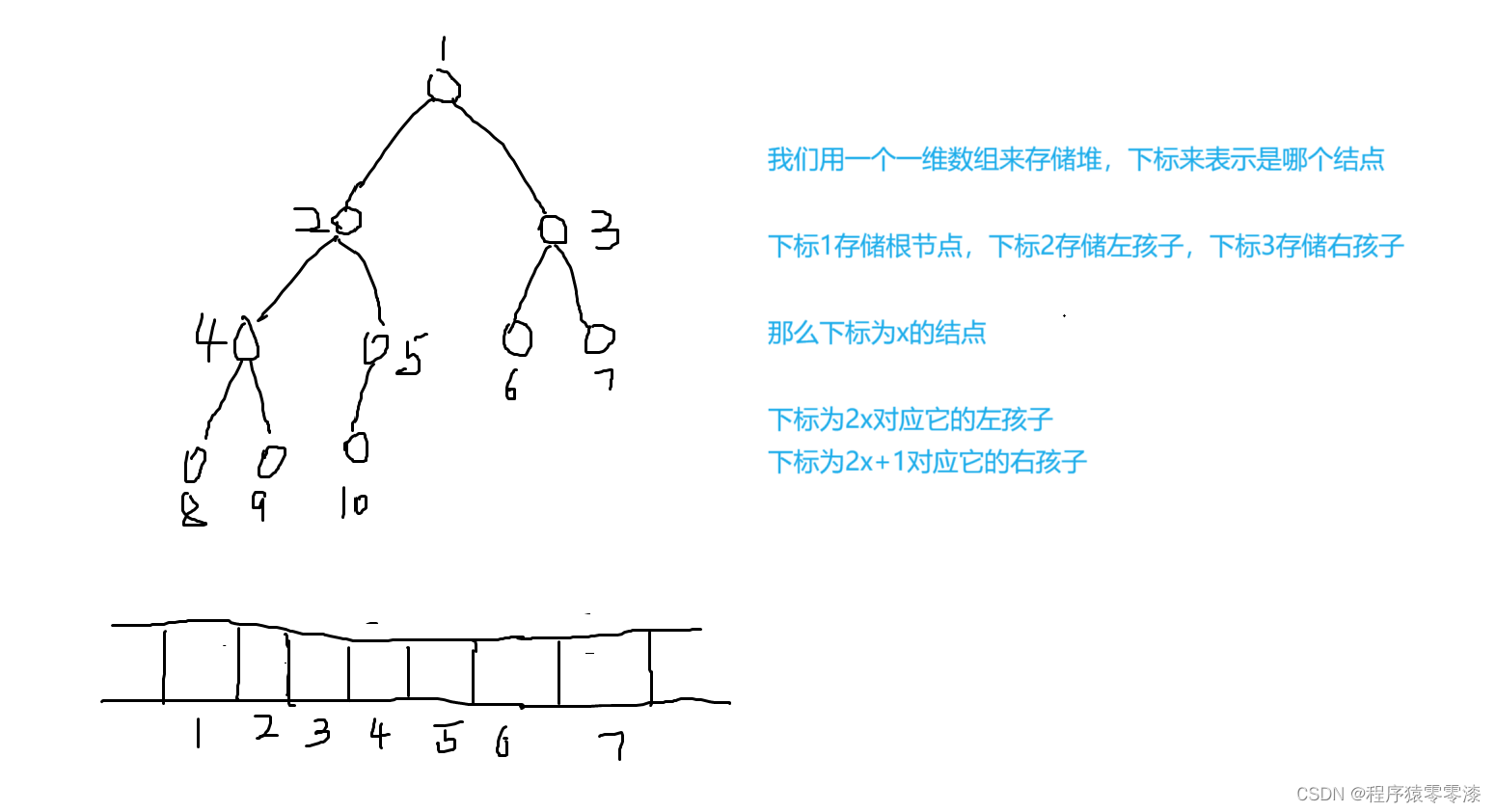
图1.1堆的存储示例图
我们用一个一维数组来存储堆的值,下标来表示是哪个结点,下标为1就存储根节点的值,下标为2存储它的左孩子的值,下标为3存储它的右孩子的值,我们就可以类比推理出任一结点的左孩子和右孩子的下标。例如下标为x的结点,它的左孩子在数组中存储的下标就是2x,它的右孩子在数组中存储的下标是2x+1。(注:下标从1开始)

2. 结点下移down
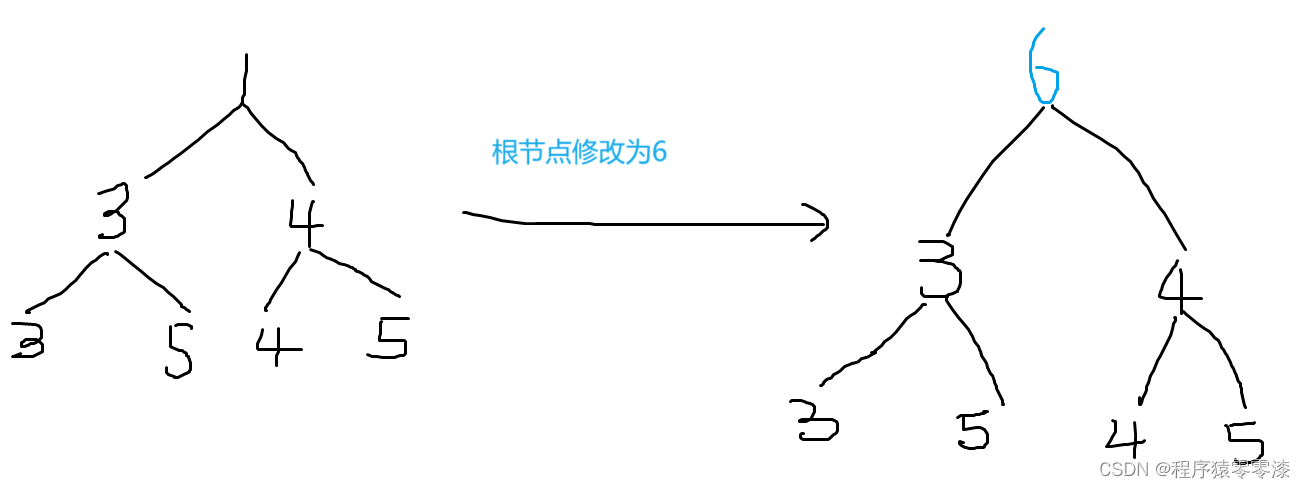
图2.1示例一
我们以一个小根堆为例,父结点的值要小于它的左右孩子结点。当我们将根节点修改为6后,此时小根堆的性质就被破坏了,那么我们就要对这个小根堆进行调整。
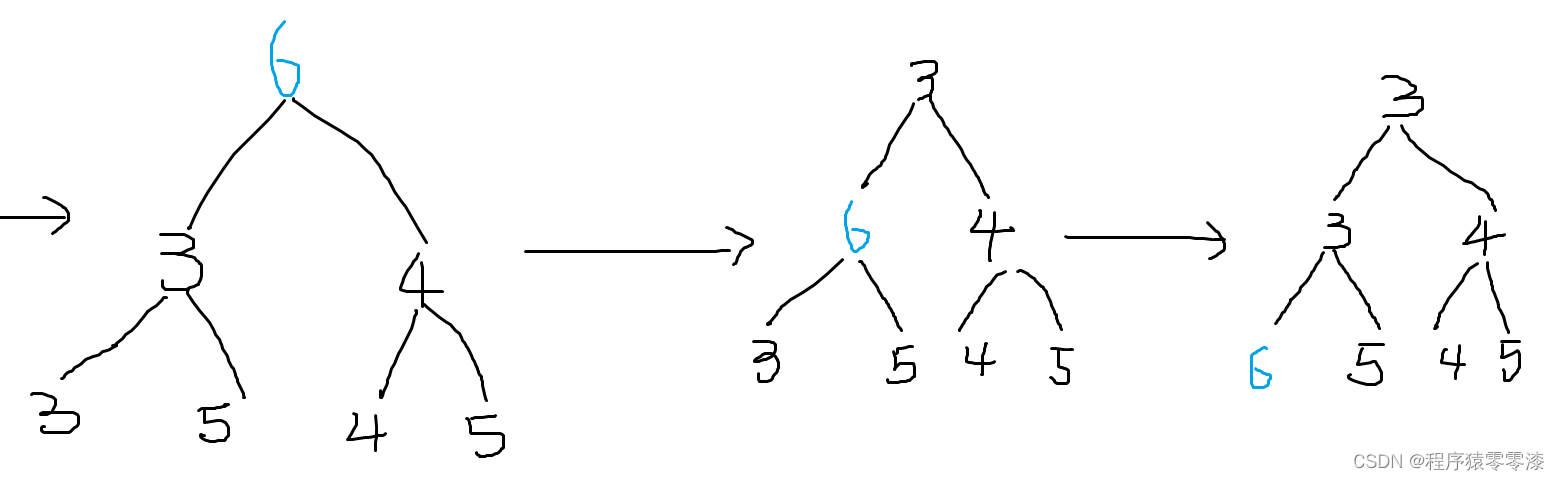
图2.2示例二
此时,我们需要与根节点的左右孩子进行比较,得出6的左孩子3是3个点中最小的,进行交换。此时小根堆的性质还没维护好,此时我们还需要将6跟它的左右孩子进行比较,得出它的左孩子3是最小的,再将6和它的左孩子进行交换,此时检查后发现,符合小根堆的性质。即我们将某一个值变大,那么在小根堆中它就要下移。
//传入结点下标public static void down(int x){int temp = x;//两个if语句来找出3个结点中最小的结点的下标if(2 * x <= size && heap[2* x] < heap[temp]){temp = 2 * x;}if (2 * x + 1 <= size && heap[2*x + 1] < heap[temp]){temp = 2 * x + 1;}//说明此时结点不是最小值,进行交换,再递归处理看是否还需要交换if(temp != x){int t = heap[temp];heap[temp] = heap[x];heap[x] = t;down(temp);}}
3.结点上移up
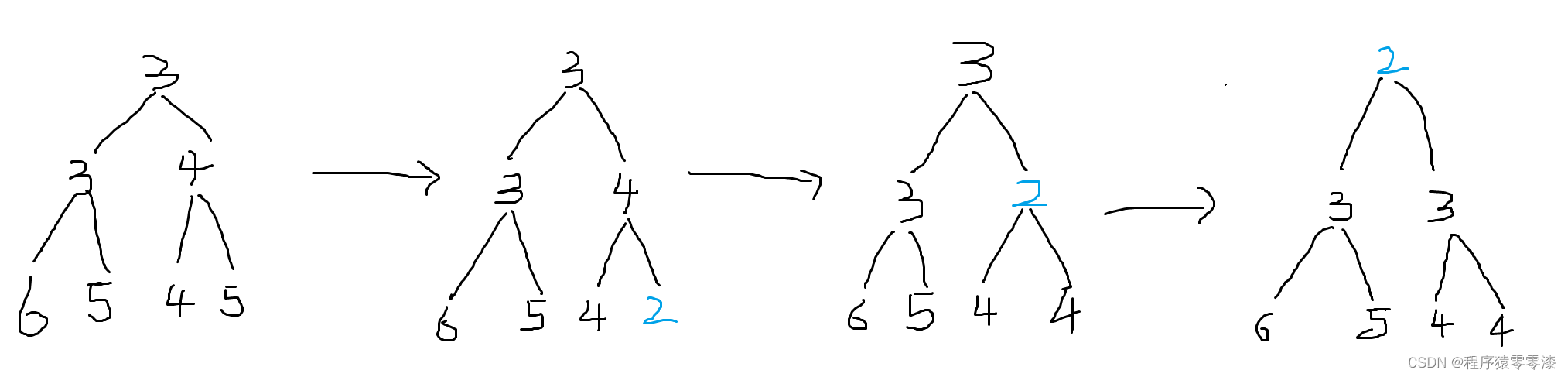
图3.1结点上移示例
当我们把最右下角的结点值修改为2,此时小根堆的性质被破坏。我们把2和它的父结点进行比较得出2就是3个结点的最小值,2跟它的父结点进行交换;然后。此时的2再跟它的父结点进行比较得出2是3个结点中的最小值,将2跟它的父结点进行交换。此时检查后,发现符合小根堆的性质。可以看出如果值变大的话,我们需要进行结点上移操作,即结点上移来维护小根堆的性质。
up操作我们只需要跟父亲结点比就可以了。
//传入结点下标public static void up(int x){int t = x;int temp = x / 2;if(temp >= 1 && heap[temp] > heap[t]){t = temp;}if(t != x){int arr = heap[t];heap[t] = heap[x];heap[x] = arr;up(t);}}
4.堆的基本操作
我们引入一个一维整型数组heap来存储堆,一个整型变量size来表示堆中最后一个元素的下标或者堆中的元素个数。(数组下标0不用,我们从下标为1开始存储)
向堆中插入一个数:我们则直接在数组最后一个元素后面加入一个值,最后一个元素的下标为size即head[++size] = x;此时我们要预防堆的性质是否被破坏,那么我们直接执行结点上移操作即可。up(size);
求堆中的最小值:小根堆中的根节点就是堆中的最小值即head[1]。
删除最小值:即我们将根节点删除了,在一维数组中第一个元素我们很难删除,但是最后一个元素很容易删除,我们只需要用最后一个元素将根节点覆盖,然后将堆的大小减1即head[1] = head[size];dowx(1)来让结点下移来维护堆的性质。
删除任意一个元素:删除下标为k的结点值,我们还是用堆中的最后一个元素将这个元素值进行覆盖,然后将堆的大小减1即head[k] = head[size];size--;如果结点值变大的进行结点下移,结点值变小进行结点下移,那么我们直接down(k);up(k);因为它最后只会执行这两个操作中的一个,这样小根堆的性质也会被维护。
修改任意一个元素:修改下标为k的元素为x,那么我们需要head[k] = x;如果结点值变大的进行结点下移,结点值变小进行结点下移,那么我们直接down(k);up(k);因为它最后只会执行这两个操作中的一个,这样小根堆的性质也会被维护。

5.堆的初始化
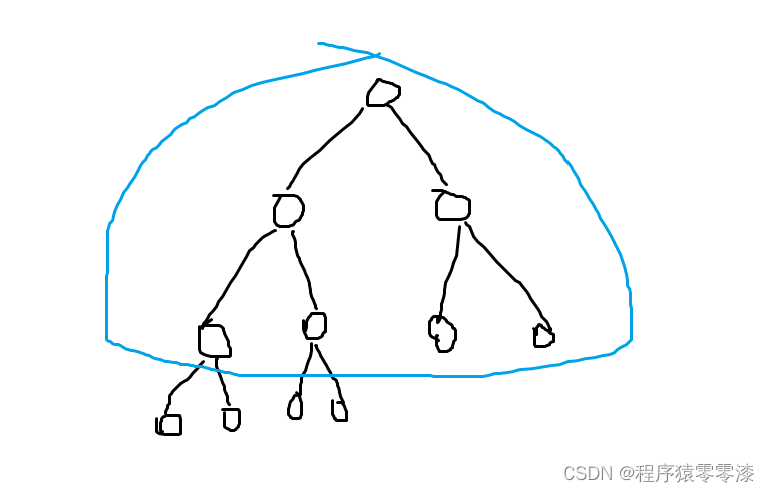
图5.1示例图
因为我们需要初始化建造一个小根堆,那么我们只需要从倒数第2层开始每一个结点进行结点下移操作就可以了。最后一层是叶子节点不需要进行结点下移操作。
for(int i = 1; i <= n; i++){heap[i] = sc.nextInt();}size = n;//初始化建堆for(int i = n / 2;i > 0;i--){down(i);}三、代码如下
1.代码如下:
import java.io.*;
import java.util.*;
public class 堆排序 {static PrintWriter pw = new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out)));static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));static int N = 100010;//存储堆static int[] heap = new int[N];//堆中最后一个结点的下标,也是堆中元素的个数static int size = 0;public static void main(String[] args) throws Exception{Scanner sc = new Scanner(br);int n = sc.nextInt();int m = sc.nextInt();for(int i = 1; i <= n; i++){heap[i] = sc.nextInt();}size = n;//初始化建堆for(int i = n / 2;i > 0;i--){down(i);}while (m-- > 0){//打印最小值pw.print(heap[1] +" ");//删除堆中的根节点,然后维护小根堆性质heap[1] = heap[size];size--;down(1);}pw.flush();}//传入结点下标public static void down(int x){int temp = x;//两个if语句来找出3个结点中最小的结点的下标if(2 * x <= size && heap[2* x] < heap[temp]){temp = 2 * x;}if (2 * x + 1 <= size && heap[2*x + 1] < heap[temp]){temp = 2 * x + 1;}//说明此时结点不是最小值,进行交换,再递归处理看是否还需要交换if(temp != x){int t = heap[temp];heap[temp] = heap[x];heap[x] = t;down(temp);}}//传入结点下标public static void up(int x){int t = x;int temp = x / 2;if(temp >= 1 && heap[temp] > heap[t]){t = temp;}if(t != x){int arr = heap[t];heap[t] = heap[x];heap[x] = arr;up(t);}}
}
2.读入数据:
5 3
4 5 1 3 23.代码运行结果
1 2 3 总结
上述通过一些堆的基本操作来完成堆排序,后续会专门再写一次博客来详细介绍模拟堆的各种操作。
相关文章:

堆排序-java
这次主要讲了堆排序和堆的基本构造,下一期会详细讲述堆的各种基本操作。 文章目录 前言 一、堆排序 1.题目描述 2.堆 二、算法思路 1.堆的存储 2. 结点下移down 3.结点上移up 4.堆的基本操作 5.堆的初始化 三、代码如下 1.代码如下: 2.读入数据ÿ…...

Android MIPI屏配置
参考资料:RockChip发布的DRM Display Driver Development Guide手册,以及网上大量相关博客资料 首先要拿到《屏幕硬件规格书》和《DataSheet》,软件配置主要依靠DataSheet提供数据支持。 查阅DataSheet里面on sequence和off sequence说明&a…...

C#面:.Net、ASP.Net、C#、VisualStudio之间的关系是什么
C#是一种编程语言,它是由微软开发的,用于开发各种类型的应用程序,包括桌面应用程序、Web应用程序和移动应用程序等。C#是一种面向对象的语言,它具有强大的类型安全性和丰富的库支持。 .NET是一个软件开发框架,它由微软…...

OpenMV学习笔记3——画图函数汇总
画图,即在摄像头对应位置画出图形,对于需要反馈信息的程序来说很直观。就如上一篇文章颜色识别当中的例子一样,我们在识别出的色块上画出矩形方框,并在中间标出十字,可以直观的看到OpenMV现在识别出的色块。 目录 一…...

【大模型应用开发极简入门】构建新闻稿生成器:提示词的使用与基于事实的提示词
文章目录 一. 提示词怎么写二. 完整代码三. 基于事实的prompt GPT-4和ChatGPT等LLM专用于生成文本。我们可以使用GPT-4和ChatGPT在各种场景中生成文本,举例如下。 电子邮件合同或正式文档创意写作逐步行动计划头脑风暴广告职位描述 对于本项目,我们将创建…...

JAVA和爬虫,那个值得学习
如果你是初学者,建议先从基础的编程语言学起,比如Java,它能为你打下坚实的编程基础,并且在未来转学其他语言或技术时更加容易。随着编程基础的建立,你可以根据自己的兴趣或职业规划,学习爬虫技术作为补充技…...
Vue.js 与 TypeScript(1) :项目配置、props标注类型、emits标注类型
像 TypeScript 这样的类型系统可以在编译时通过静态分析检测出很多常见错误。这减少了生产环境中的运行时错误,也让我们在重构大型项目的时候更有信心。通过 IDE 中基于类型的自动补全,TypeScript 还改善了开发体验和效率。 一、项目配置 在使用 npm cr…...

【考试100】安全员B证《建设工程安全生产技术》单选题
题库来源:考试100 【考试100】安全员B证《建设工程安全生产技术》单选题 1.在悬空部位作业时,操作人员应( ) A.遵守操作规定 B.进行安全技术交底 C.戴好安全帽 D.系好安全带 【考试100答案】:D…...
linux进阶的一些操作以及知识点------习题集(实践)
请创建以你姓名全拼的用户luwenhua,将其设置为免密登录,切换到luwenhua用户,打开终端,完成以下操作 (一)bash脚本基础练习 1)第一题:请在终端里定义两个用户变量num120,…...

提莫攻击 ---- 模拟算法
题目链接 题目: 分析: 如果两次攻击的时间差是>中毒的持续时间duration, 那么第一次攻击的中毒时间就是duration如果两次攻击的时间差是< 中毒的持续时间duration, 那么第一次攻击的持续时间就是这个时间差假设攻击了n次, 那么我们从第一次攻击开始计算时间差, 那么当我…...

SpringBootWeb 篇-深入了解 Spring 异常处理、事务管理和配置文件参数配置化、yml 配置文件
🔥博客主页: 【小扳_-CSDN博客】 ❤感谢大家点赞👍收藏⭐评论✍ 文章目录 1.0 配置文件 1.1 yml 配置文件 1.2 参数配置化 1.2.1 使用 Value 注解注入单个配置参数 1.2.2 使用 ConfigurationProperties 注解将一组相关配置参数注入到一个类中…...
重学java 55. 集合 Set接口
我救自己万万次,铮铮劲草,绝不动摇 —— 24.6.2 一、Set集合介绍 Set和Map密切相关的 Map的遍历需要先变成单列集合,只能变成set集合 二、HashSet集合的介绍和使用 1.概述 HashSet是Set接口的实现类 2.特点 a、元素唯一 b、元素无序 c、无索引…...

spring项目修改时间格式
一、配置方式 在application.yml上添加 spring:jackson:date-format: yyyy-MM-dd HH:mm:sstime-zone: GMT8 二、注解方式 1、添加依赖 <dependency><groupId>com.fasterxml.jackson.core</groupId><artifactId>jackson-annotations</artifactId&…...
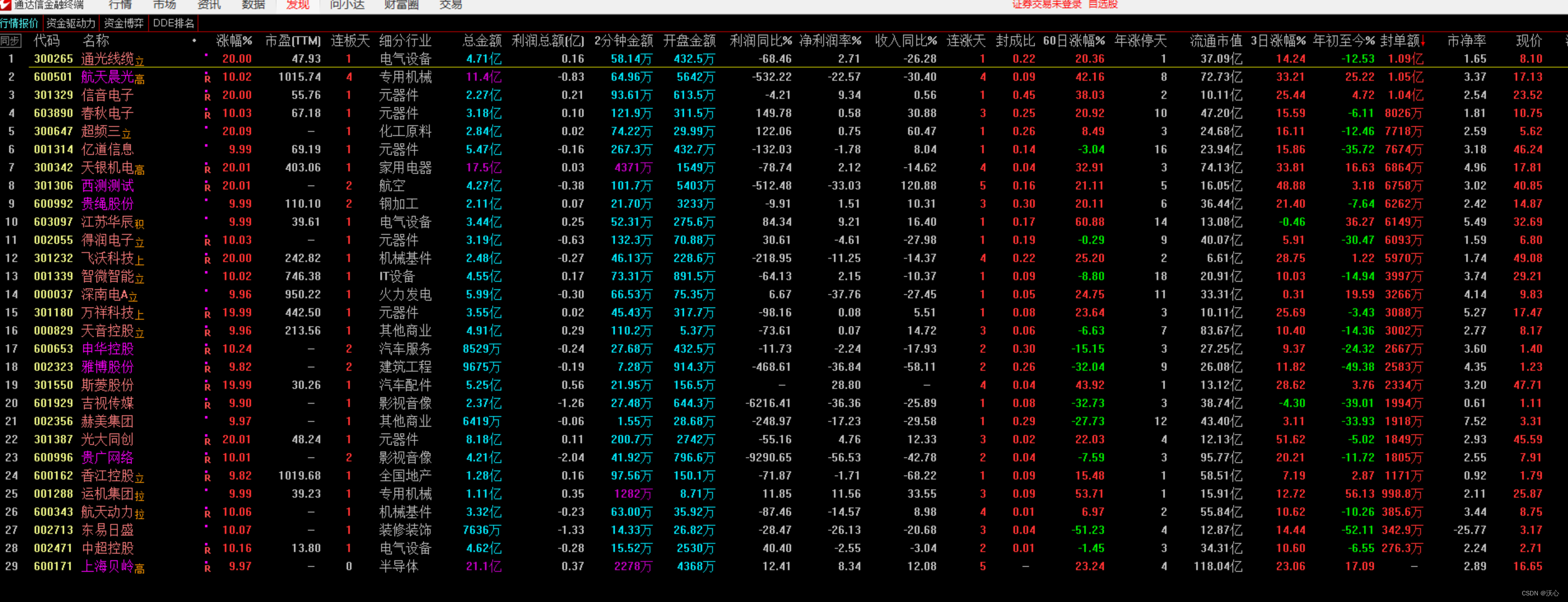
每周统计-20240531
用于测试程序的稳定性: 龙虎榜: 成交额: 封成比: 收盘前放量: 开盘抢筹: 封单额:...

【工具】探索 DOU:每用户数据使用量
缘分让我们相遇乱世以外 命运却要我们危难中相爱 也许未来遥远在光年之外 我愿守候未知里为你等待 我没想到为了你我能疯狂到 山崩海啸没有你根本不想逃 我的大脑为了你已经疯狂到 脉搏心跳没有你根本不重要 🎵 邓紫棋《光年之外》 什么是 DOU…...
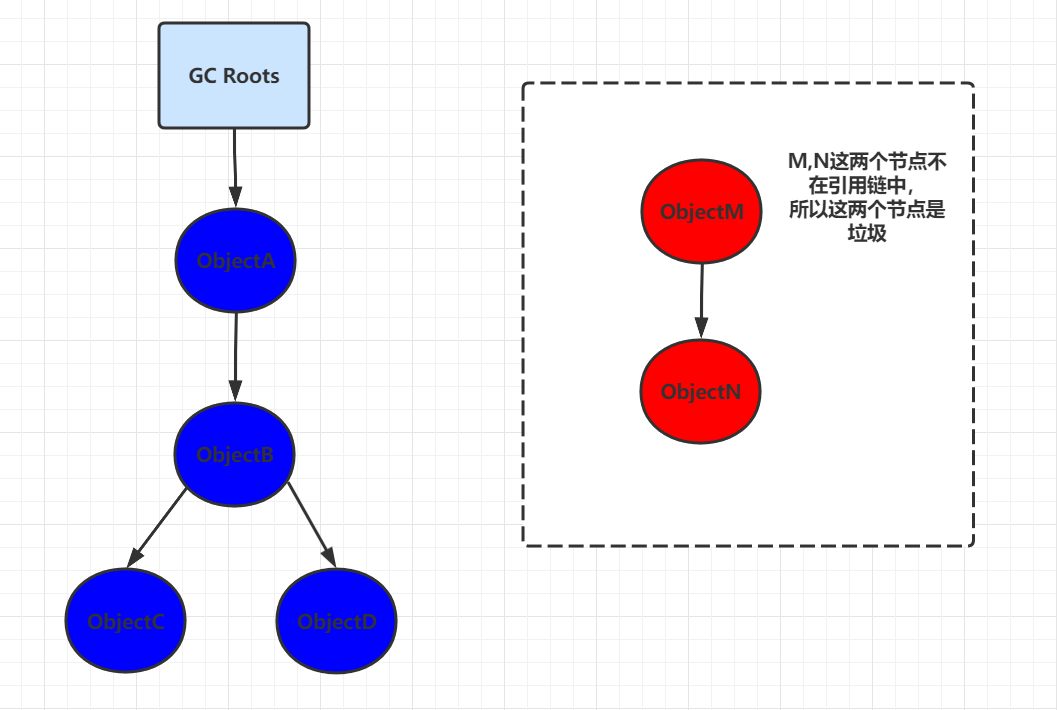
JVM之垃圾判断的详细解析
垃圾判断 垃圾介绍 垃圾:如果一个或多个对象没有任何的引用指向它了,那么这个对象现在就是垃圾 作用:释放没用的对象,清除内存里的记录碎片,碎片整理将所占用的堆内存移到堆的一端,以便 JVM 将整理出的内…...

07- Redis 中的 HyperLogLog 数据类型和应用场景
1. 介绍 Redis HyperLogLog 是 Redis 2.8.9 版本新增的数据类型,是一种用于【统计基数】的数据集合类型,基数统计就是指统计一个集合中不重复的元素个数。但要注意,HyperLogLog 的统计规则是基于概率完成的,不是非常准确…...
jenkins应用2-freestyle-job
1.jenkins应用 1.jenkins构建的流程 1.使用git参数化构建,用标签区分版本 2.git 拉取gitlab远程仓库代码 3.maven打包项目 4.sonarqube经行代码质量检测 5.自定义制作镜像发送到远程仓库harbor 6.在远程服务器上拉取代码启动容器 这个是构建的整个过程和步骤…...
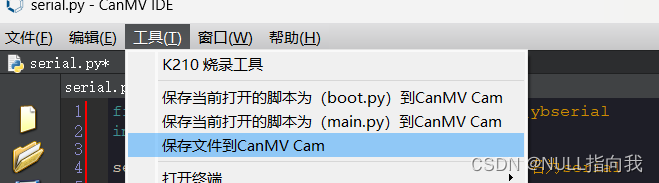
K210视觉识别模块学习笔记1:第一个串口程序_程序烧录与开机启动
今日开始学习K210视觉识别模块:简单的认识与串口程序 亚博智能的K210视觉识别模块...... 固件库版本: canmv_yahboom_v2.1.1.bin 既然K210作为一个视觉识别外设模块来使用,我认为第一个程序 就没必要学点灯之类的了,直接学习串口如何配置开始为妥&…...
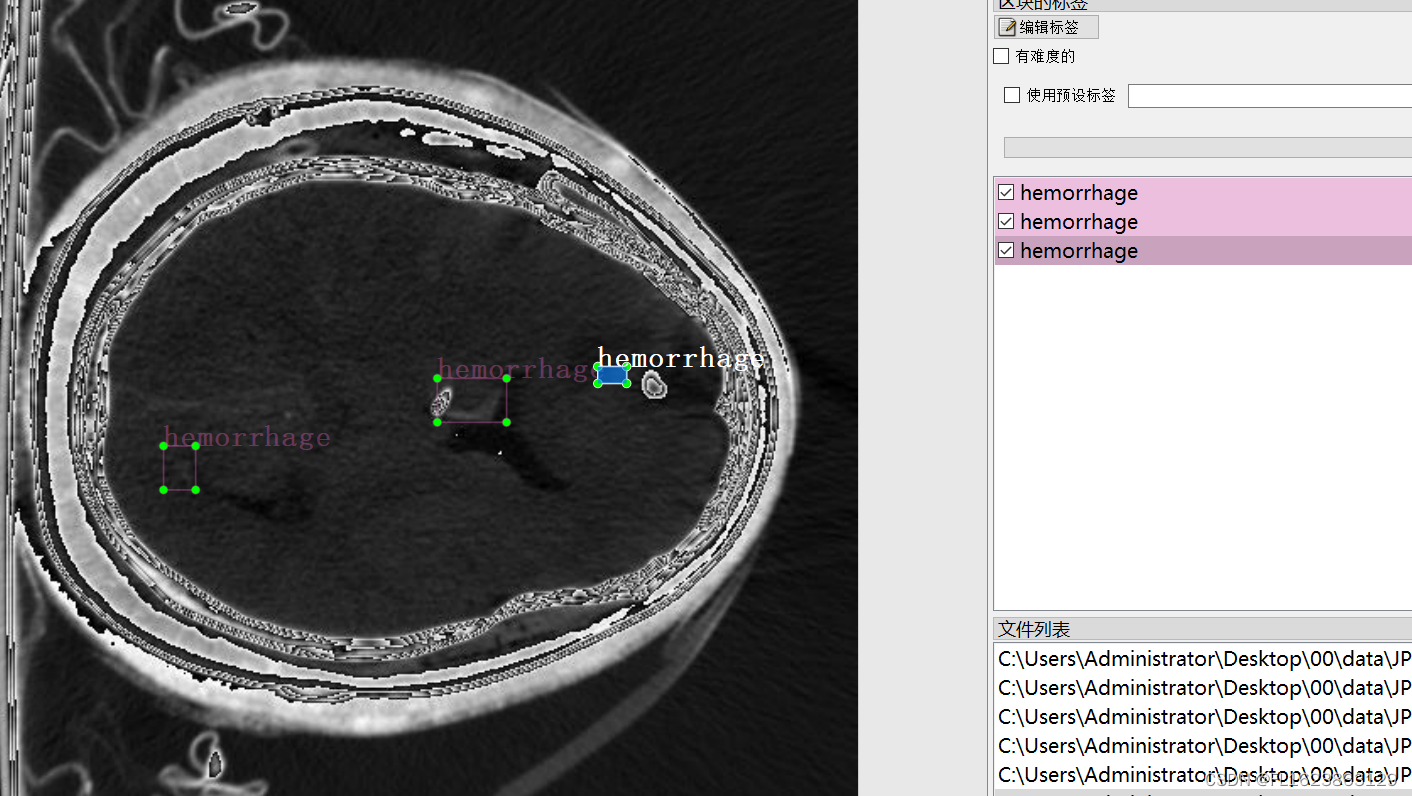
[数据集][目标检测]脑溢血检测数据集VOC+YOLO格式767张2类别
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):767 标注数量(xml文件个数):767 标注数量(txt文件个数):767 标注类别…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...
