模拟集成电路(6)----单级放大器(共源共栅级 Cascode Stage)
模拟集成电路(6)----单级放大器(共源共栅级 Cascode Stage)
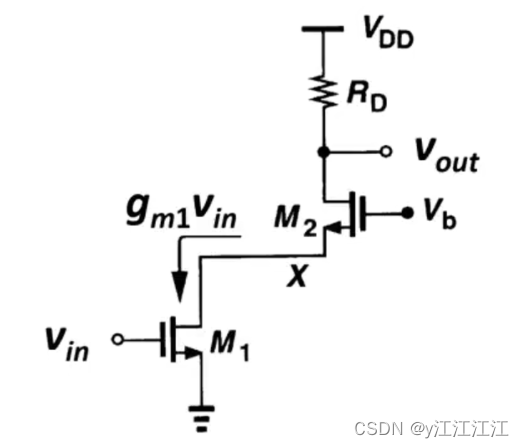
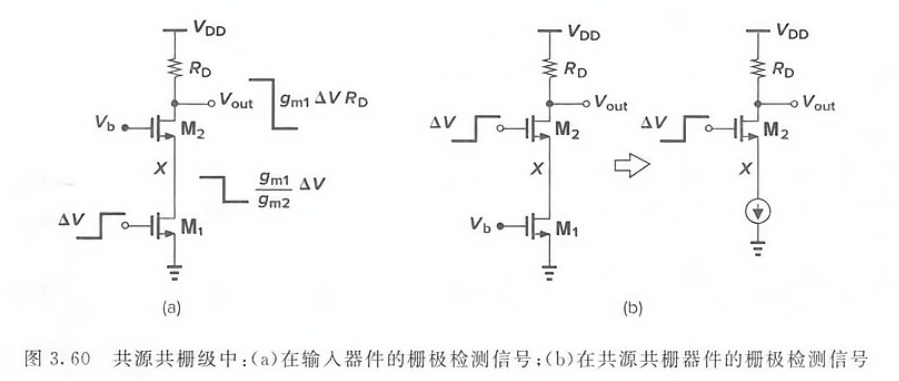
大信号分析
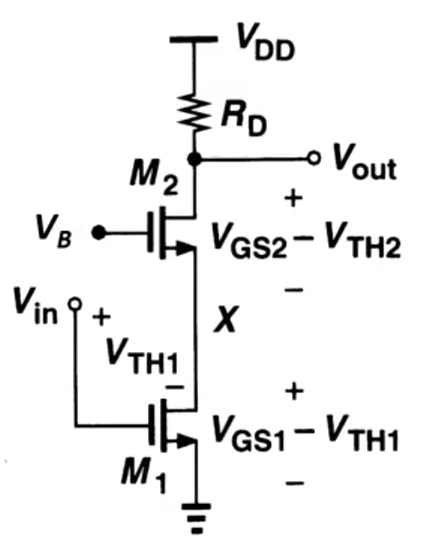
对M1
V x ≥ V i n − V T H 1 V x = V B − V G S 2 V B ≥ V i n − V T H 1 + V G S 2 V_{x}\geq V_{in}-V_{TH1}\quad V_{x}=V_{B}-V_{GS2}\\V_{B}\geq V_{in}-V_{TH1}+V_{GS2} Vx≥Vin−VTH1Vx=VB−VGS2VB≥Vin−VTH1+VGS2
对M2
V o u t ≥ V B − V T H 2 V o u t ≥ V i n − V T H 1 + V G S 2 − V T H 2 V o u t ≥ V O D 1 + V O D 2 \begin{aligned}&V_{out}\geq V_{B}-V_{TH2}\\&V_{out}\geq V_{in}-V_{TH1}+V_{GS2}-V_{TH2}\\&V_{out}\geq V_{OD1}+V_{OD2}\end{aligned} Vout≥VB−VTH2Vout≥Vin−VTH1+VGS2−VTH2Vout≥VOD1+VOD2
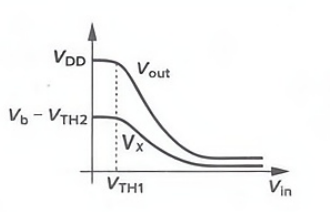
输入输出电阻
W h e n V i n < V T H 1 , M 1 a n d M 2 a r e o f f , V o u t = V D D , V x = V B − V T H 2 \begin{aligned}&\mathrm{When~}V_{in}<V_{TH1},\mathrm{M}_{1}\mathrm{~and~}\mathrm{M}_{2}\mathrm{~are~off},V_{out}=V_{DD},V_{x}=V_{B}-V_{TH2}\end{aligned} When Vin<VTH1,M1 and M2 are off,Vout=VDD,Vx=VB−VTH2
W h e n V i n > V T H 1 , V o u t d r o p s , − V G S 2 increases, resulting in a drop of V X \begin{aligned}&\mathrm{When~}V_{\mathrm{in}}>V_{\mathrm{TH}1},V_{\mathrm{out}}\mathrm{drops},\\&-V_{GS2}\text{increases, resulting in a drop of }V_{X}\end{aligned} When Vin>VTH1,Voutdrops,−VGS2increases, resulting in a drop of VX
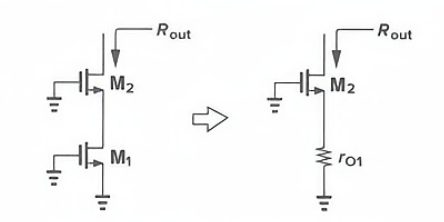
R o u t = [ 1 + ( g m 2 + g m b 2 ) r O 2 ] r O 1 + r O 2 = r O 1 + r O 2 + ( g m 2 + g m b 2 ) r O 2 r O 1 R_{out}=[1+(g_{m2}+g_{mb2})r_{O2}]r_{O1}+r_{O2}\\=r_{O1}+r_{O2}+(g_{m2}+g_{mb2})r_{O2}r_{O1} Rout=[1+(gm2+gmb2)rO2]rO1+rO2=rO1+rO2+(gm2+gmb2)rO2rO1
i f g m r O > > 1 , t h e n R o u t ≈ ( g m 2 + g m b 2 ) r O 2 r O 1 ≈ g m 2 r O 2 r O 1 if \ g_{m}r_{O}>>1,\quad\mathrm{then}\quad R_{out}\approx(g_{m2}+g_{mb2})r_{O2}r_{O1}\approx g_{m2}r_{O2}r_{O1} if gmrO>>1,thenRout≈(gm2+gmb2)rO2rO1≈gm2rO2rO1
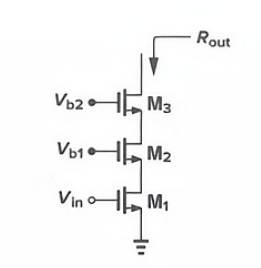
R o u t ≈ ( g m 3 + g m b 3 ) r O 3 R S ≈ g m 3 r O 3 R S ‾ R S ≈ g m 2 r O 2 r O 1 → R o u t ≈ g m 3 r O 3 ⋅ g m 2 r O 2 ⋅ r o 1 \begin{aligned}&R_{out}\approx(g_{m3}+g_{mb3})r_{O3}R_{S}\approx\underline{g_{m3}r_{O3}R_{S}}\\&R_{S}\approx g_{m2}r_{O2}r_{O1}\\&\to R_{out}\approx g_{m3}r_{O3}\cdot g_{m2}r_{O2}\cdot r_{o1}\end{aligned} Rout≈(gm3+gmb3)rO3RS≈gm3rO3RSRS≈gm2rO2rO1→Rout≈gm3rO3⋅gm2rO2⋅ro1
小信号分析
增益
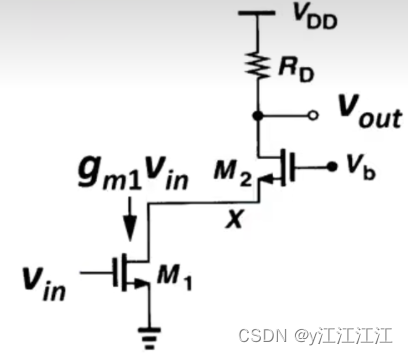
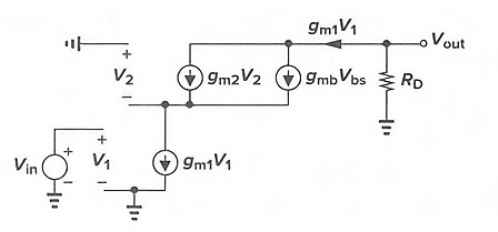
A ν = − g m 1 R D A_{\nu}=-g_{m1}R_{D} Aν=−gm1RD
如若是电流源负载

A v = − G m r o u t A_v=-G_mr_{out} Av=−Gmrout
G m ≈ g m 1 G_m{\approx}g_{m1} Gm≈gm1
A ν ≈ − g m 1 ⋅ g m 2 r o 2 r o 1 = − g m 1 r o 1 ⋅ g m 2 r o 2 A_{\nu}\approx-g_{m1}\cdot g_{m2}r_{o2}r_{o1}=-g_{m1}r_{o1}\cdot g_{m2}r_{o2} Aν≈−gm1⋅gm2ro2ro1=−gm1ro1⋅gm2ro2
可以结合课本3.21去理解
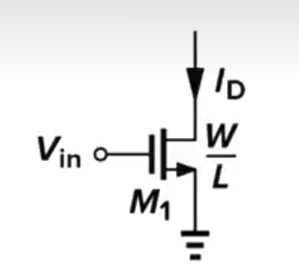
g m = 2 I D μ n C o x W L r o = 1 λ I D A i n t = g m r o g_{m}=\sqrt{2I_{\mathrm{D}}\mu_{\mathrm{n}}C_{\mathrm{ox}}\frac{W}{L}}\\r_{\mathrm{o}}=\frac{1}{\lambda I_{\mathrm{D}}}\\A_{\mathrm{int}}=g_{m}r_{\mathrm{o}} gm=2IDμnCoxLWro=λID1Aint=gmro
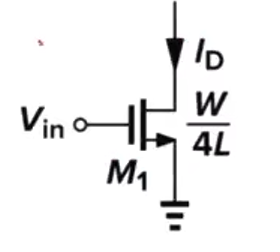
g m 1 = g m 2 r o l = 4 r o A i n t l = 2 A i n t g_{m1}=\frac{g_{\mathrm{m}}}{2}\\r_{\mathrm{ol}}=4r_{\mathrm{o}}\\A_{\mathrm{intl}}=2A_{\mathrm{int}} gm1=2gmrol=4roAintl=2Aint

g m 2 = g m r o 2 = A i n t r o A int 2 = A int 2 g_{m2}=g_{m}\\r_{\mathrm{o2}}=A_{\mathrm{int}}r_{\mathrm{o}}\\A_{\operatorname{int}2}=A_{\operatorname{int}}^2 gm2=gmro2=AintroAint2=Aint2
用PMOS cascode电流源作负载
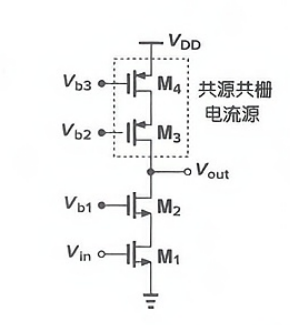
r o u t n ≈ g m 2 r o 2 ⋅ r o 1 r o u t p ≈ g m 3 r o 3 ⋅ r o 4 \begin{aligned}r_{outn}&\approx g_{m2}r_{o2}\cdot r_{o1}\\r_{outp}&\approx g_{m3}r_{o3}\cdot r_{o4}\end{aligned} routnroutp≈gm2ro2⋅ro1≈gm3ro3⋅ro4
A ν ≈ − g m 1 ⋅ ( r o u t n ∥ r o u t p ) ≈ − g m 1 ⋅ ( g m 3 r o 3 ⋅ r o 4 ∥ g m 2 r o 2 ⋅ r o 1 ) \begin{aligned}A_{\nu}&\approx-g_{m1}\cdot(r_{outn}\parallel r_{outp})\\&\approx-g_{m1}\cdot(g_{m3}r_{o3}\cdot r_{o4}\parallel g_{m2}r_{o2}\cdot r_{o1})\end{aligned} Aν≈−gm1⋅(routn∥routp)≈−gm1⋅(gm3ro3⋅ro4∥gm2ro2⋅ro1)
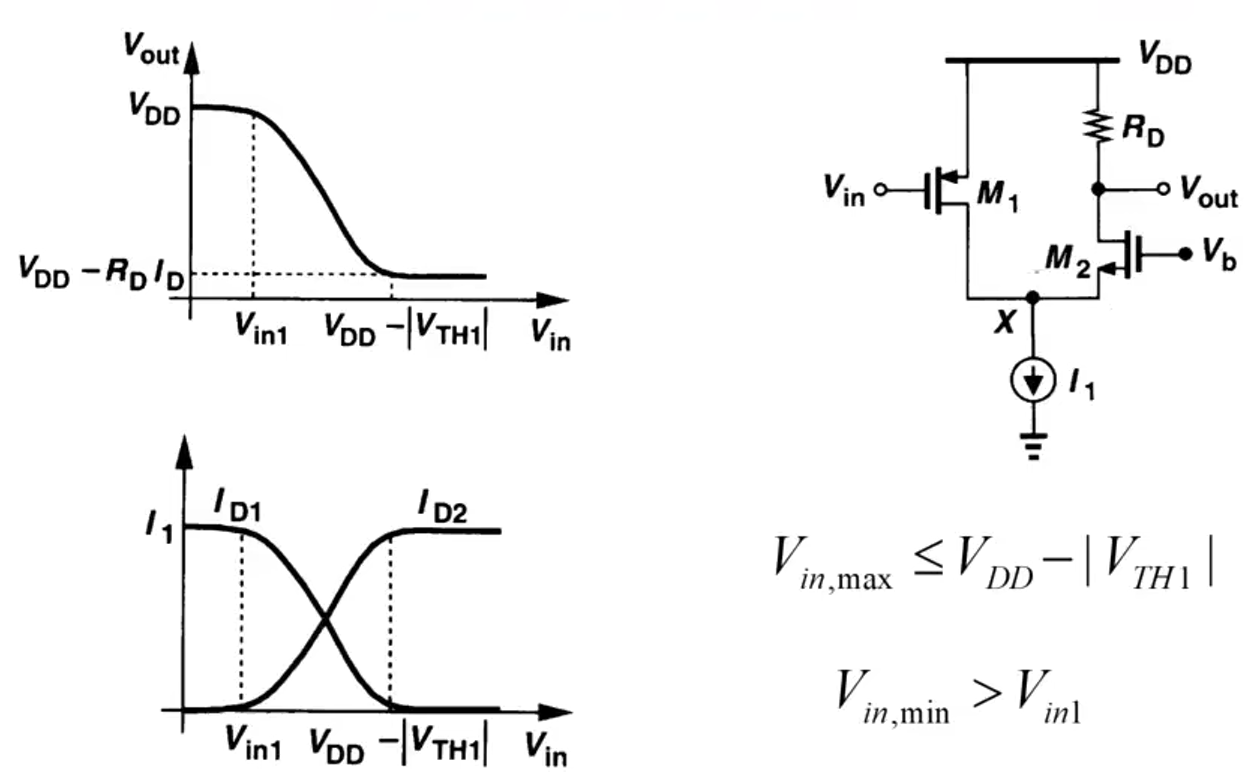
V o u t max ≤ V D D − V O D 3 − V O D 4 V_{out\max}\leq V_{DD}-V_{OD3}-V_{OD4} Voutmax≤VDD−VOD3−VOD4
V o u t , m i n ≥ V O D 1 + V O D 2 V_{out,min}\geq V_{OD1}+V_{OD2} Vout,min≥VOD1+VOD2
相关文章:

模拟集成电路(6)----单级放大器(共源共栅级 Cascode Stage)
模拟集成电路(6)----单级放大器(共源共栅级 Cascode Stage) 大信号分析 对M1 V x ≥ V i n − V T H 1 V x V B − V G S 2 V B ≥ V i n − V T H 1 V G S 2 V_{x}\geq V_{in}-V_{TH1}\quad V_{x}V_{B}-V_{GS2}\\V_{B}\geq V_{in}-V_{TH1}V_{GS2} Vx…...
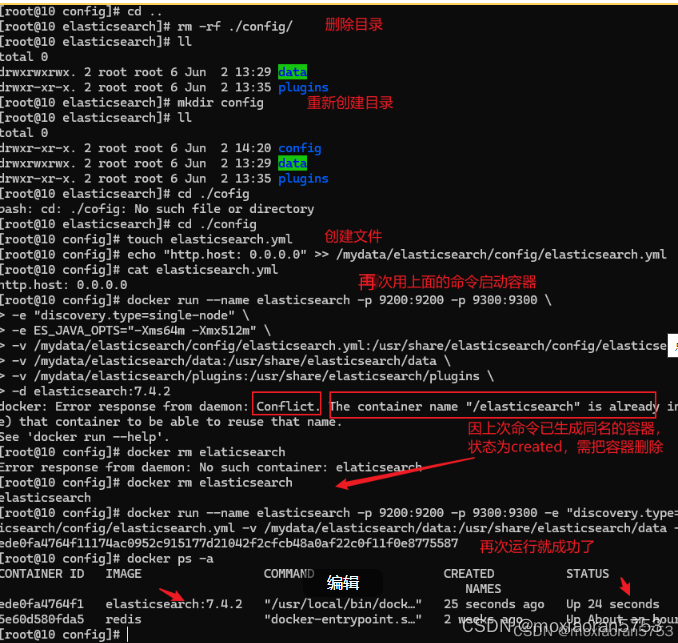
docker以挂载目录启动容器报错问题的解决
拉取镜像: docker pull elasticsearch:7.4.2 docker pull kibana:7.4.2 创建实例: mkdir -p /mydata/elasticsearch/configmkdir -p /mydata/elasticsearch/dataecho "http.host: 0.0.0.0" >> /mydata/elasticsearch/config/elasti…...
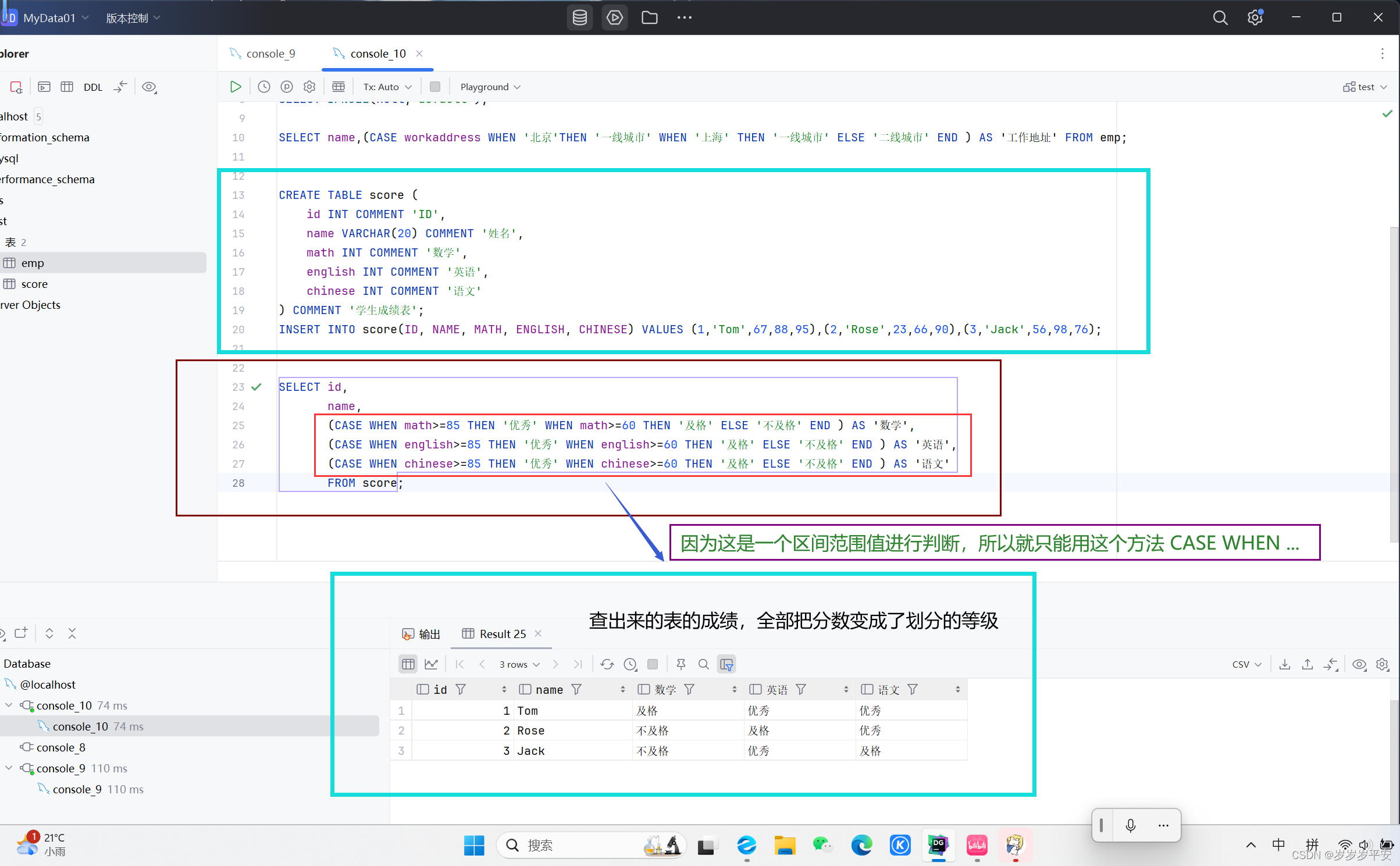
MySQL—函数—流程控制函数(基础)
一、引言 接下来,我们就进入函数的最后一个部分:流程函数。而流程控制函数在我们的日常开发过程是很有用的。 流程控制函数在我们 sql 语句当中,经常用来实现条件的筛选,从而提高语句的一个执行效率。 我们主要介绍以下4个流程控…...
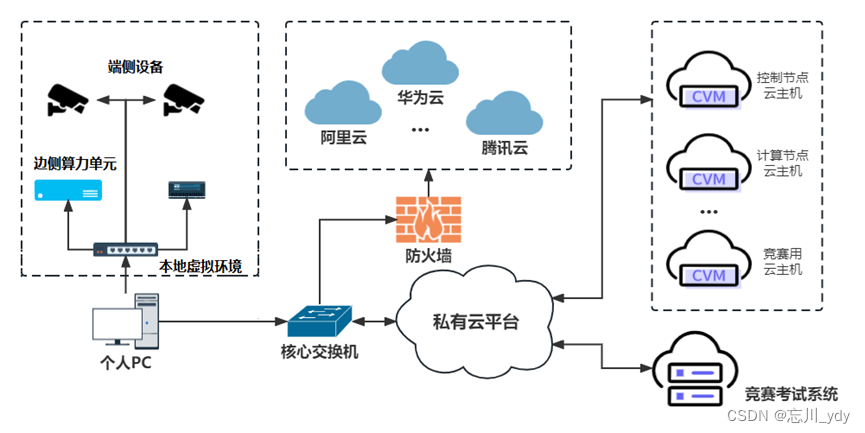
2023年全国职业院校技能大赛(高职组)“云计算应用”赛项赛卷7(私有云)
#需要资源(软件包及镜像)或有问题的,可私聊博主!!! #需要资源(软件包及镜像)或有问题的,可私聊博主!!! #需要资源(软件包…...
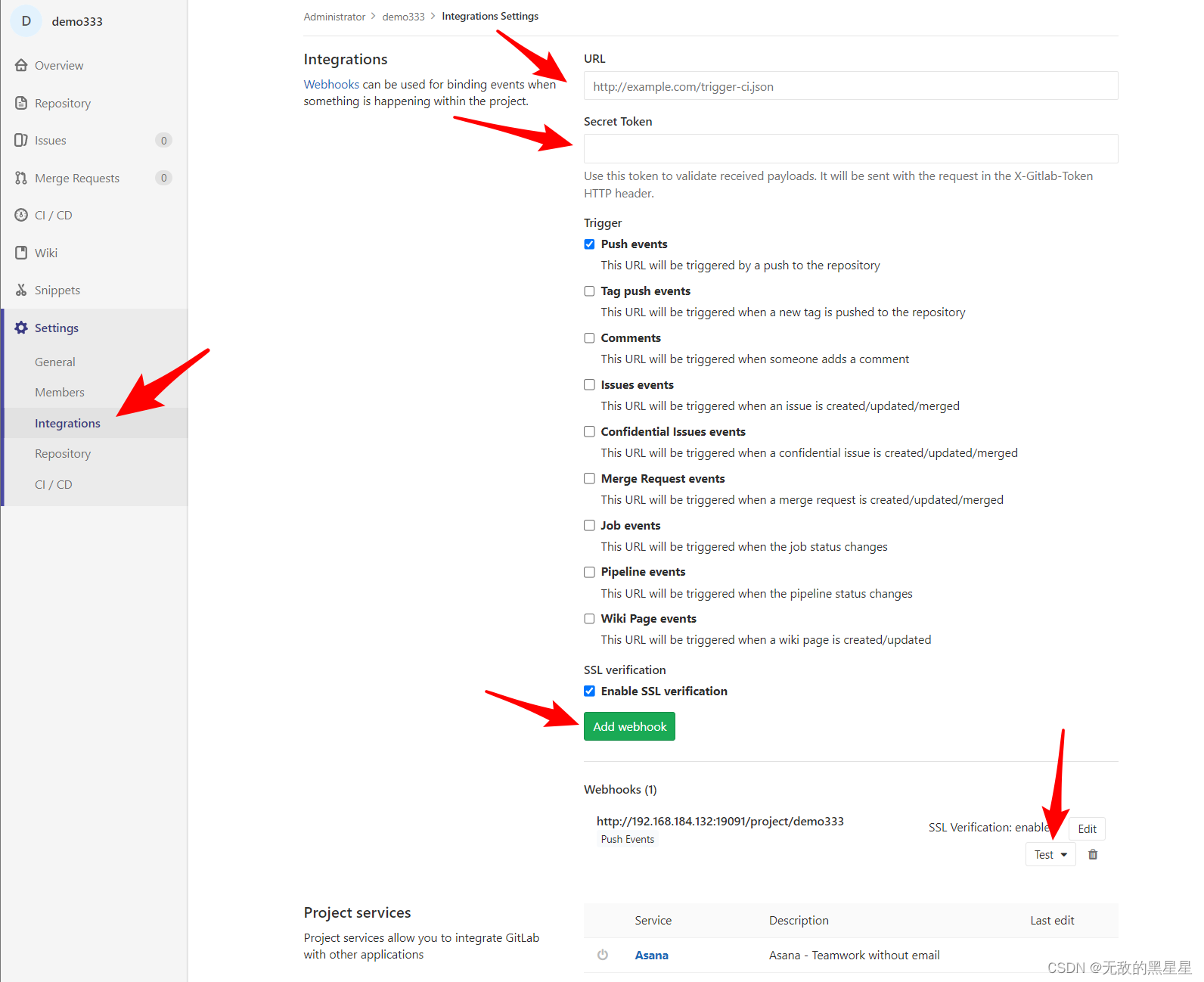
Jenkins、GitLab部署项目
1、安装JDK 1.1、下载openJdk11 yum -y install fontconfig java-11-openjdk1.2、查看安装的版本号 java -version1.3、配置环境变量 vim /etc/profile在最底部添加即可 export JAVA_HOME/usr/lib/jvm/java-11-openjdk-11.0.23.0.9-2.el7_9.x86_64 export PATH$JAVA_HOME/…...
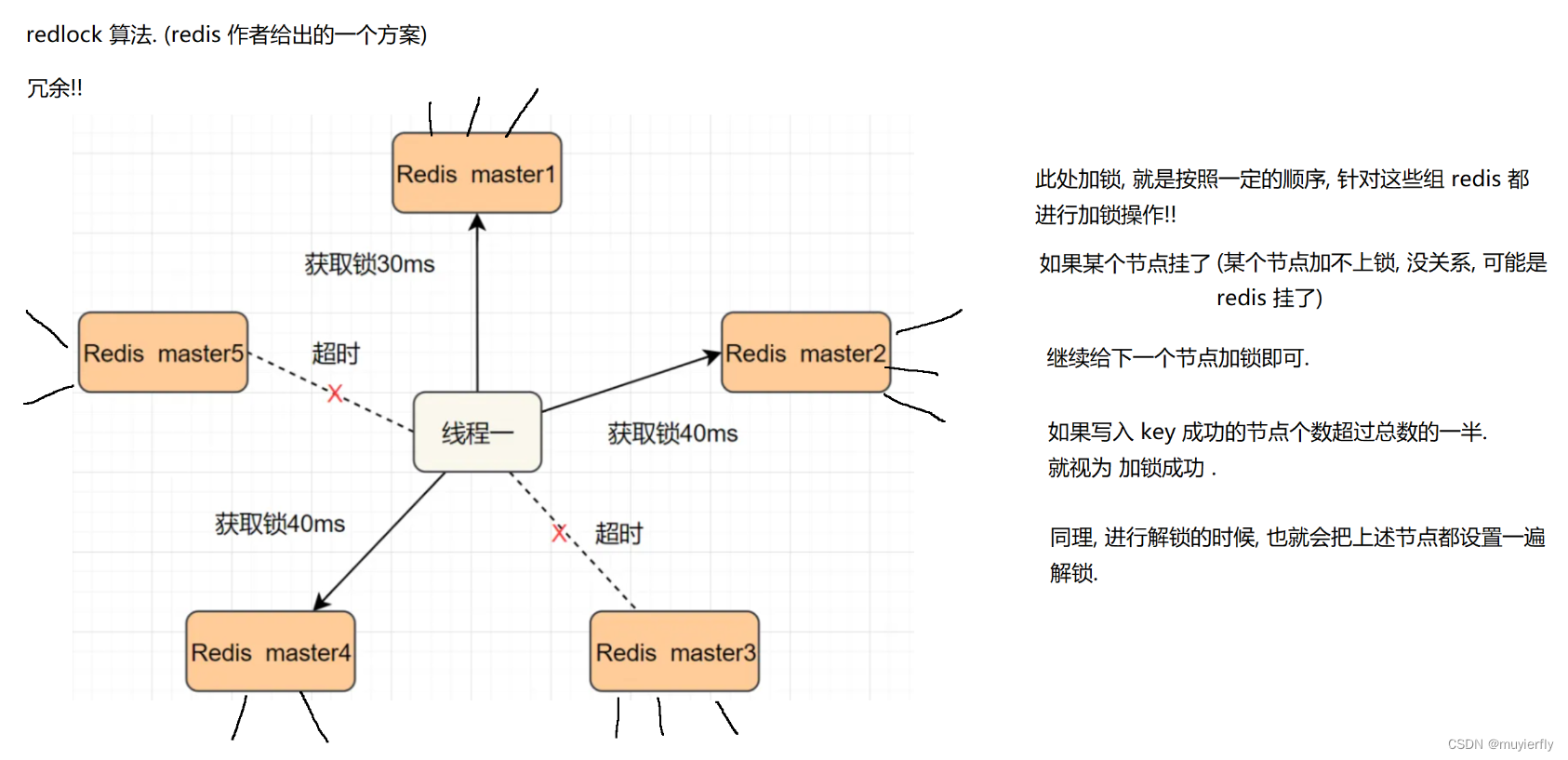
21.Redis之分布式锁
1.什么是分布式锁 在⼀个分布式的系统中, 也会涉及到多个节点访问同⼀个公共资源的情况. 此时就需要通过 锁 来做互斥控制, 避免出现类似于 "线程安全" 的问题. ⽽ java 的 synchronized 或者 C 的 std::mutex, 这样的锁都是只能在当前进程中⽣效, 在分布式的这种多…...

Mysql基础学习:mysql8 JSON字段查询操作
文章目录 一、查询JSON中某个属性值为XXX的数据量1、方式一2、方式二 二、查询的JSON中的value并去除双引号 一、查询JSON中某个属性值为XXX的数据量 1、方式一 select count(*)from table_namewhere JSON_CONTAINS(json-> $.filed1, "xxx")or JSON_CONTAINS(jso…...

搭建基于Django的博客系统数据库迁移从Sqlite3到MySQL(四)
上一篇:搭建基于Django的博客系统增加广告轮播图(三) 下一篇:基于Django的博客系统之用HayStack连接elasticsearch增加搜索功能(五) Sqlite3数据库迁移到MySQL 数据库 迁移原因 Django 的内置数据库 SQL…...

24年护网工具,今年想参加护网的同学要会用
24年护网工具集 吉祥学安全知识星球🔗http://mp.weixin.qq.com/s?__bizMzkwNjY1Mzc0Nw&mid2247483727&idx1&sndb05d8c1115a4539716eddd9fde4e5c9&chksmc0e47813f793f105017fb8551c9b996dc7782987e19efb166ab665f44ca6d900210e6c4c0281&scene21…...
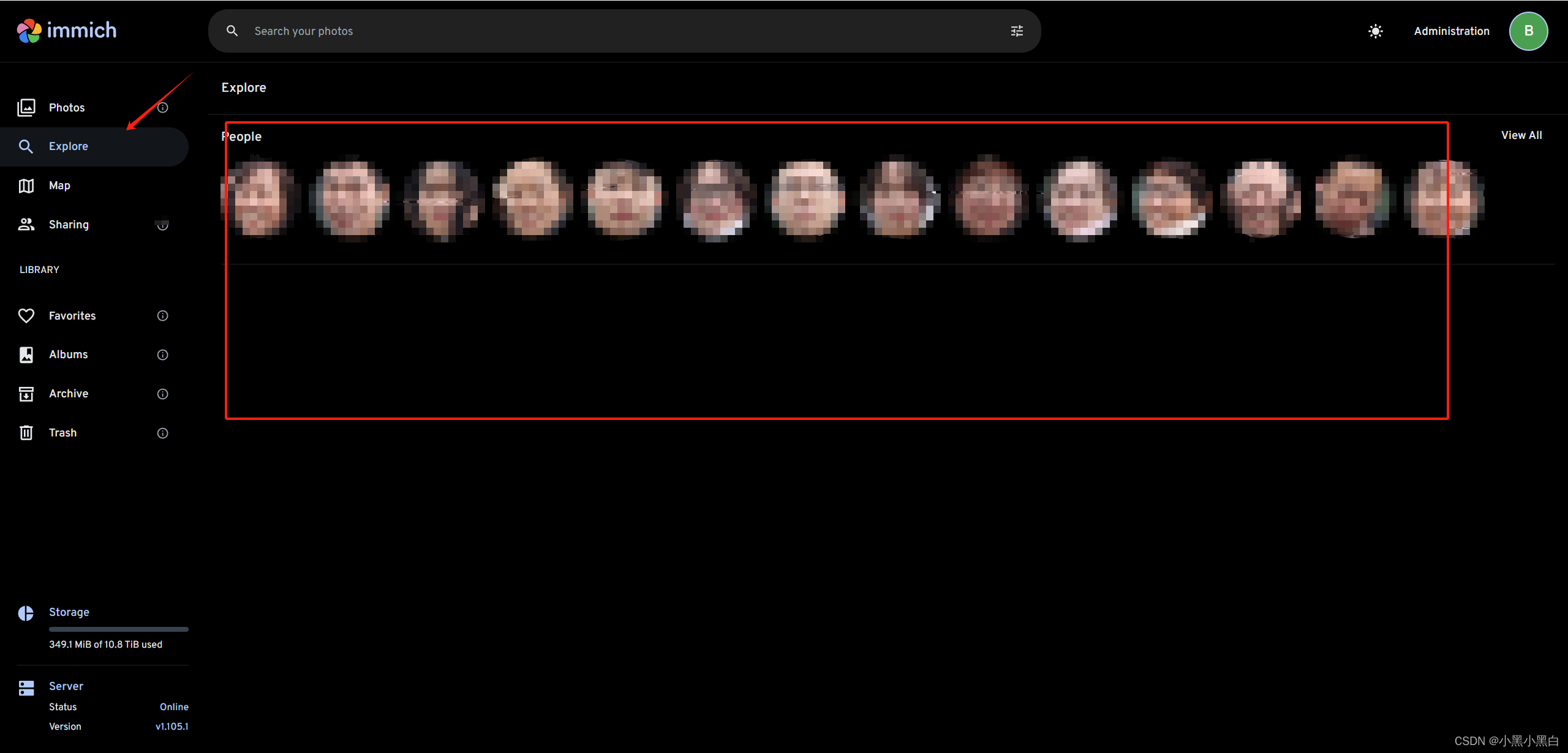
解决TrueNas Scale部署immich后人脸识别失败,后台模型下载异常,immich更换支持中文搜索的CLIP大模型
这个问题搞了我几天终于解决了,搜遍网上基本没有详细针对TrueNas Scale部署immich应用后,CLIP模型镜像下载超时导致人脸识别失败,以及更换支持中文识别的CLIP模型的博客。 分析 现象:TrueNas Scale安装immich官方镜像应用后&…...

面试高频问题----2
一、进程、线程、协程有什么区别? 1.进程:进程是操作系统中独立运行的程序实例,每个进程都有自己的内存空间和系统资源;进程之间相互独立,每个进程有自己的内存地址空间,一个进程无法直接访问另一个进程的…...

Nginx的配置文件-详细使用说明
Nginx的配置文件是Nginx服务器运行的核心,它决定了Nginx如何响应和处理各种请求。以下是对Nginx配置文件(通常名为nginx.conf)的详细解析,按照常见的结构和配置项进行分类: 1. 全局块 user:指定Nginx运行的用户和用户组。例如:user nginx;worker_processes:指定工作进…...

YOLOv5改进 | 卷积模块 | 提高网络的灵活性和表征能力的动态卷积【附代码+小白可上手】
💡💡💡本专栏所有程序均经过测试,可成功执行💡💡💡 轻量级卷积神经网络由于其低计算预算限制了CNNs的深度(卷积层数)和宽度(通道数),…...

23、linux系统文件和日志分析
linux文件系统与日志分析 文件时存储在硬盘上的,硬盘上的最小存储单位是扇区,每个扇区大大小是512字节。 inode:元信息(文件的属性 权限,创建者,创建日期等) block:块,…...
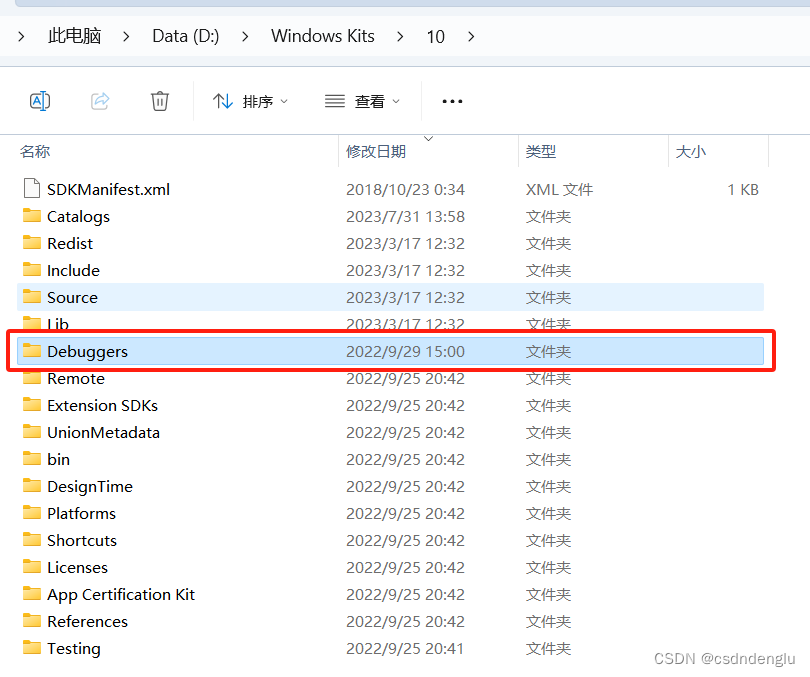
安装VS2017后,离线安装Debugging Tools for Windows(QT5.9.2使用MSVC2017 64bit编译器)
1、背景 安装VS2017后,Windows Software Development Kit - Windows 10.0.17763.132的Debugging Tools for Windows默认不会安装,如下图。这时在QT5.9.2无法使用MSVC2017 64bit编译器。 2、在线安装 如果在线安装参考之前的文章: Qt5.9.2初…...
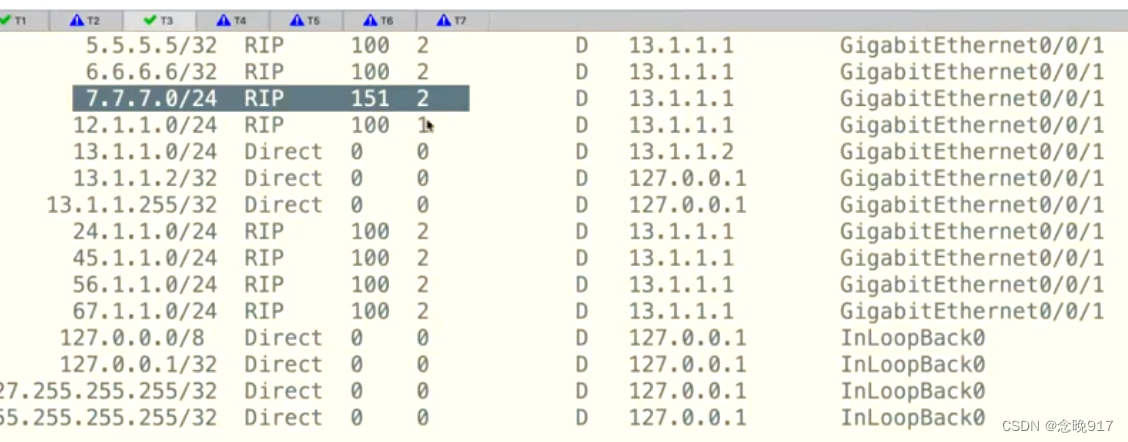
路由策略实验2
对R7,重发布直连路由 对R2,做双向 对R3同样 先不改优先级 查看,知道所有给R3的路由为151,全部为OSPF。 知道了是错误的,先把3,4之间的线路断掉 接着对R3,让优先级全部回到100(displa…...
Linux网络-守护进程版字典翻译服务器
文章目录 前言一、pid_t setsid(void);二、守护进程翻译字典服务器(守护线程版)效果图 前言 根据上章所讲的后台进程组和session会话,我们知道如果可以将一个进程放入一个独立的session,可以一定程度上守护该进程。 一、pid_t se…...

Python 推导式详解:高效简洁的数据处理技巧
推导式是 Python 提供的一种简洁而强大的语法,用于创建列表、集合和字典。它可以让代码更简洁、更易读,同时提高运行效率。 基本语法 列表推导式 基本语法: [expression for item in iterable if condition]示例: # 生成平方…...

车联网安全入门——ICSim模拟器使用
文章目录 车联网安全入门——ISCim模拟器使用介绍主要特点:使用场景: 安装使用捕获can流量candumpcansnifferwiresharkSavvyCAN主要特点:使用场景: 重放can报文cansendSavvyCAN 总结 车联网安全入门——ISCim模拟器使用 …...

leetcode - 20.有效的括号(LinkedHashMap)
leetcode题目有效的括号,分类是easy,但是博主前前后后提交了几十次才通过,现在记录一下使用Java语言的写法。 题目链接: 20.有效的括号 题目描述: 给定一个只包括 (,),{,},[&…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...

【堆垛策略】设计方法
堆垛策略的设计是积木堆叠系统的核心,直接影响堆叠的稳定性、效率和容错能力。以下是分层次的堆垛策略设计方法,涵盖基础规则、优化算法和容错机制: 1. 基础堆垛规则 (1) 物理稳定性优先 重心原则: 大尺寸/重量积木在下…...

数据分析六部曲?
引言 上一章我们说到了数据分析六部曲,何谓六部曲呢? 其实啊,数据分析没那么难,只要掌握了下面这六个步骤,也就是数据分析六部曲,就算你是个啥都不懂的小白,也能慢慢上手做数据分析啦。 第一…...
