【NOIP普及组】税收与补贴问题
【NOIP普及组】税收与补贴问题
| 💖The Begin💖点点关注,收藏不迷路💖 |
每样商品的价格越低,其销量就会相应增大。现已知某种商品的成本及其在若干价位上的销量(产品不会低于成本销售),并假设相邻价位间销量的变化是线性的且在价格高于给定的最高价位后,销量以某固定数值递减。(我们假设价格及销售量都是整数)
对于某些特殊商品,不可能完全由市场去调节其价格。这时候就需要政府以税收或补贴的方式来控制。(所谓税收或补贴就是对于每个产品收取或给予生产厂家固定金额的货币)问题求解:
你是某家咨询公司的项目经理,现在你已经知道政府对某种商品的预期价格,以及在各种价位上的销售情况。要求你确定政府对此商品是应收税还是补贴的最少金额(也为整数),才能使商家在这样一种政府预期的价格上,获取相对其他价位上的最大总利润。
总利润=单位商品利润*销量单位商品利润=单位商品价格-单位商品成本(-税金 or +补贴)
输入:
第一行为政府对某种商品的预期价,第二行有两个整数,第一个整数为商品成本,第二个整数为以成本价销售时的销售量,以下若干行每行都有两个整数,第一个为某价位时的单价,第二个为此时的销量,以一行-1,-1表示所有已知价位及对应的销量输入完毕,输入的最后一行为一个单独的整数表示在已知的最高单价外每升高一块钱将减少的销量。
输出:
输出有两种情况:若在政府预期价上能得到最大总利润,则输出一个单独的整数,数的正负表示是补贴还是收税,数的大小表示补贴或收税的金额最小值。若有多解,取绝对值最小的输出。
如在政府预期价上不能得到最大总利润,则输出“NO SOLUTION”。
样例输入:
31
28 130
30 120
31 110
-1 -1
15
样例输出:
4
#include <stdio.h>
#include <stdlib.h>#define N 100005 // 定义数组长度的常量typedef struct { // 定义节点结构体int c, num; // c表示单价,num表示销量
} Node;int targetC, targetNum, cut, cnt; // targetC为政府预期价,targetNum为政府预期价对应的销量,cut为每升高一块钱将减少的销量,cnt表示数组中节点个数
Node nodes[N]; // 定义节点数组int compare(const void *a, const void *b) { // 定义比较函数return ((Node*)b)->num - ((Node*)a)->num; // 根据销量从大到小排序
}void solve() { // 求解最优税收或补贴的函数int ans = 0, p, q, x, y; // ans表示税收或补贴的金额,p、q、x、y都是中间变量int flag1 = 0, flag2 = 0; // flag1、flag2表示是否需要进行税收或补贴while (1) { // 迭代直到得到最优解flag1 = 0, flag2 = 0;p = (targetC - nodes[0].c + ans) * targetNum; // 计算政府预期价下,所有节点的总销售额(不考虑税收或补贴)q = (targetC - nodes[0].c - ans) * targetNum; // 计算政府预期价下,所有节点的总销售额(不考虑税收或补贴)for (int i = 0; i < cnt; i++) { // 遍历所有节点if (nodes[i].num <= 0) // 如果该节点销量为0,跳出循环break;x = (nodes[i].c - nodes[0].c + ans) * nodes[i].num; // 计算该节点在政府预期价下的总销售额(不考虑税收或补贴)y = (nodes[i].c - nodes[0].c - ans) * nodes[i].num; // 计算该节点在政府预期价下的总销售额(不考虑税收或补贴)if (x > p) // 如果该节点在政府预期价下销售额高于所有节点的总销售额,需要进行补贴flag1 = 1;if (y > q) // 如果该节点在政府预期价下销售额低于所有节点的总销售额,需要进行税收flag2 = 1;if (flag1 && flag2) // 如果需要进行补贴和税收,则跳出循环break;}if (flag1 && flag2) { // 如果需要进行补贴和税收,则增加税收或补贴的金额ans++;continue;}x = nodes[cnt-1].c; // 获取最高价位y = nodes[cnt-1].num; // 获取最高价位对应的销量while (y > 0) { // 不断增加税收或补贴的金额,直到找到最优解x++; // 增加单价y -= cut; // 减少销量if ((x - nodes[0].c + ans) * y > p) // 如果补贴金额太小导致总销售额低于政府预期价下的总销售额,需要进行补贴flag1 = 1;if ((x - nodes[0].c - ans) * y > q) // 如果税收金额太小导致总销售额高于政府预期价下的总销售额,需要进行税收flag2 = 1;if (flag1 && flag2) // 如果需要进行补贴和税收,则跳出循环break;}if (flag1 && !flag2) { // 如果需要进行补贴但不需要进行税收,则输出补贴金额printf("%d\n", -ans);return;}if (!flag1 && flag2) { // 如果需要进行税收但不需要进行补贴,则输出税收金额printf("%d\n", ans);return;}if (!flag1 && !flag2) { // 如果不需要进行补贴和税收,则输出0printf("%d\n", ans);return;}ans++; // 增加税收或补贴的金额}
}int main() { // 主函数scanf("%d", &targetC); // 输入政府预期价int x, y;while (1) { // 输入所有节点scanf("%d %d", &x, &y);if (x == -1 && y == -1) // 如果输入-1,-1则结束输入break;nodes[cnt].c = x;nodes[cnt].num = y;cnt++;}scanf("%d", &cut); // 输入每升高一块钱将减少的销量qsort(nodes, cnt, sizeof(Node), compare); // 对节点按销量从大到小排序for (int i = 0; i < cnt - 1; i++) { // 补全缺失的节点if (nodes[i+1].c - nodes[i].c > 1) { // 如果两个节点之间存在空缺for (int j = nodes[i].c + 1; j < nodes[i+1].c; j++) { // 在两个节点之间插入节点nodes[cnt].c = j;nodes[cnt].num = nodes[i].num - (nodes[i].num - nodes[i+1].num) / (nodes[i+1].c - nodes[i].c) * (j - nodes[i].c);cnt++;}}}qsort(nodes, cnt, sizeof(Node), compare); // 再次对节点按销量从大到小排序int targetExists = 0;for (int i = 0; i < cnt; i++) { // 查找政府预期价对应的销量if (nodes[i].c == targetC) {targetExists = 1;targetNum = nodes[i].num;break;}}if (!targetExists) // 如果政府预期价对应的销量不存在,需要根据最高价位和每升高一块钱将减少的销量来计算targetNum = nodes[cnt-1].num - (targetC - nodes[cnt-1].c) * cut;solve(); // 求解最优税收或补贴return 0;
}求解最优税收或补贴的问题。主要思想如下:
- 定义节点结构体,包含单价和销量两个属性。
- 定义全局变量,包括政府预期价、政府预期价对应的销量、每升高一块钱将减少的销量等。
- 输入政府预期价和节点信息,并对节点按销量从大到小进行排序。
- 补全可能存在的节点缺失,并再次按销量从大到小进行排序。
- 查找政府预期价对应的销量,如果不存在,则根据最高价位和每升高一块钱将减少的销量来计算。
- 使用solve函数求解最优税收或补贴。迭代过程中,比较各节点在政府预期价下的销售额与所有节点总销售额的大小,判断是否需要进行补贴和税收。增加税收或补贴的金额,直到找到最优解。
- 输出最优税收或补贴的金额。
总体来说,该代码通过迭代的方式,不断调整税收或补贴的金额,直到找到最优解。

| 💖The End💖点点关注,收藏不迷路💖 |
相关文章:

【NOIP普及组】税收与补贴问题
【NOIP普及组】税收与补贴问题 💖The Begin💖点点关注,收藏不迷路💖 每样商品的价格越低,其销量就会相应增大。现已知某种商品的成本及其在若干价位上的销量(产品不会低于成本销售),…...

Docker 部署 mysql 服务
linux用法 Container(容器)集合成 Services(服务) 交互集合成 Stack(堆栈)卸载可能存在的旧版本 sudo apt-get update使apt可以通过HTTPS使用存储库(repository) sudo apt-get ins…...

01- Redis 中的 String 数据类型和应用场景
1. 介绍 String 是最基本的 key-value 结构,key 是唯一标识,value 是具体的值,value 其实不仅是字符串,也可以是数字(整数或浮点数),value 最多可以容纳的数据长度是 512M。 2. 内部实现 Str…...

Android音频焦点
什么是音频焦点? 音频焦点是 API 8 中引入的一个概念。它用于传达这样一个事实:用户一次只能专注于一个音频流,例如收听音乐或播客,但不能同时关注两者。在某些情况下,多个音频流可以同时播放,但只有一个是…...

Docker安全配置
Docker安全及日志管理 文章目录 Docker安全及日志管理资源列表基础环境一、Docker安全相关介绍1.1、Docker容器与虚拟机的区别1.1.1、隔离与共享1.1.2、性能与损耗 1.2、Docker存在的安全问题1.2.1、Docker自身漏洞1.2.2、Docker源码问题 1.3、Docker架构缺陷与安全机制1.3.1、…...

文件上传之使用一个属性接收多个文件
在开发过程中,可能遇到这样的业务:文件上传时个数不定,这样我们不能枚举出所有的文件name,这种情况下我们可以使用一个name将所有的文件接收下来; html代码 <!DOCTYPE html> <html lang"en"> …...
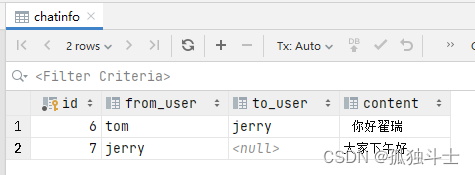
chat4-Server端保存聊天消息到mysql
本文档描述了Server端接收到Client的消息并转发给所有客户端或私发给某个客户端 同时将聊天消息保存到mysql 服务端为当前客户端创建一个线程,此线程接收当前客户端的消息并转发给所有客户端或私发给某个客户端同时将聊天消息保存到mysql 本文档主要总结了将聊天…...

vivo鄢楠:基于OceanBase 的降本增效实践
在3 月 20 日的2024 OceanBase 数据库城市行中,vivo的 体系与流程 IT 部 DBA 组总监鄢楠就“vivo 基于 OceanBase 的降本增效实践”进行了主题演讲。本文为该演讲的精彩回顾。 vivo 在1995年于中国东莞成立,作为一家全球领先的移动互联网智能终端公司&am…...
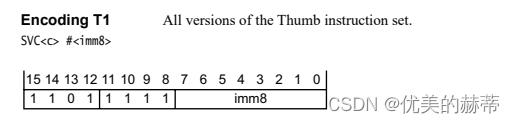
arm cortex-m架构 SVC指令详解以及其在freertos的应用
1. 前置知识 本文基于arm cortex-m架构描述, 关于arm cortex-m的一些基础知识可以参考我另外几篇文章: arm cortex-m 架构简述arm异常处理分析c语言函数调用规范-基于arm 分析 2 SVC指令 2.1 SVC指令位域表示 bit15 - bit12:条件码&#…...

k8s笔记——kubernetes中的三种IP
kubernetes概念 Master:集群控制节点,每个集群需要至少一个master节点负责集群的管控 Node:工作负载节点,由master分配容器到这些node工作节点上,然后node节点上的docker负责容器的运行 Pod:kubernetes的…...

Golang | Leetcode Golang题解之第127题单词接龙
题目: 题解: func ladderLength(beginWord string, endWord string, wordList []string) int {wordId : map[string]int{}graph : [][]int{}addWord : func(word string) int {id, has : wordId[word]if !has {id len(wordId)wordId[word] idgraph a…...
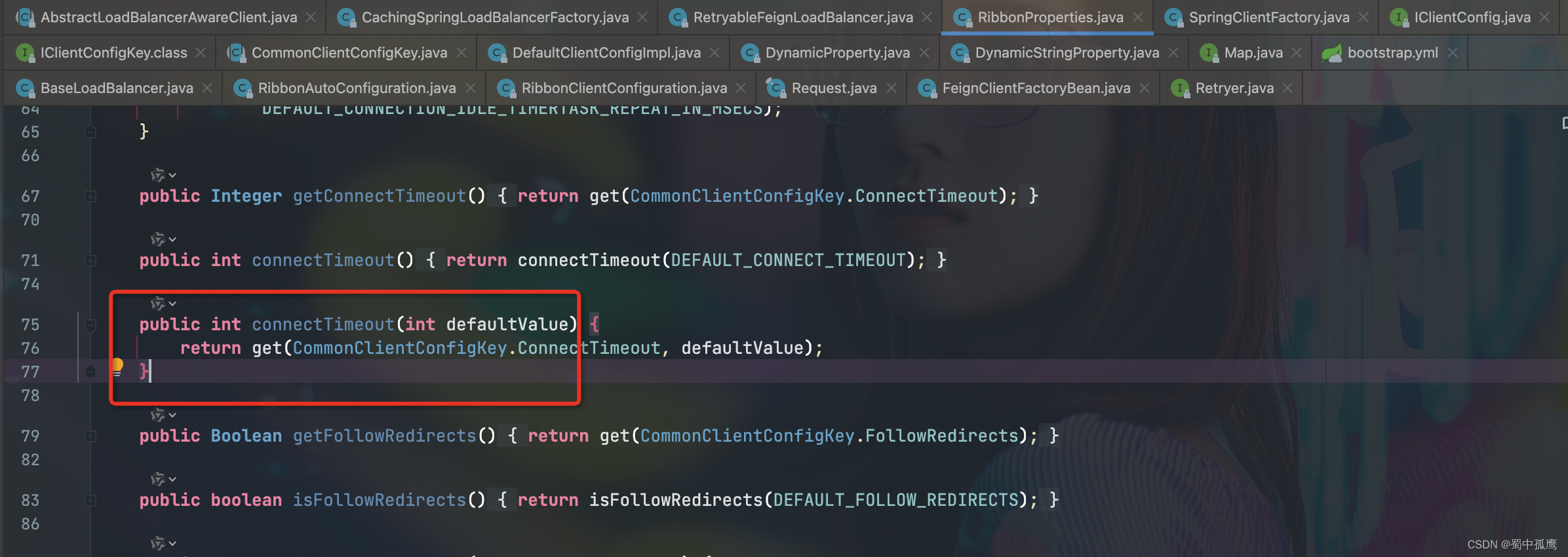
微服务中feign远程调用相关的各种超时问题
1. 引言 在spring cloud微服中,feign远程调用可能是大家每天都接触到东西,但很多同学却没咋搞清楚这里边的各种超时问题,生产环境可能会蹦出各种奇怪的问题。 首先说下结论: 1)只使用feign组件,不使用ribbion组件&…...

springboot整合chatgpt,并且让其可以记录上下文
整合很简单,不过需要几个小条件 1.必须要有openai官方的key 2.国内需要有代理服务器或者国外的服务器把项目部署出去也没问题 我没有使用spring的springAI,听说很方便,日后有机会去体验体验,我今天用了两种方式整合了gpt 1.Ch…...

CTP前端:解码数字世界的魔法师
CTP前端:解码数字世界的魔法师 CTP前端,一个充满神秘与魅力的职业,他们在数字世界中挥舞着魔法棒,创造着令人惊叹的奇迹。那么,CTP前端究竟是做什么的呢?让我们从四个方面、五个方面、六个方面和七个方面&…...

rabbitmq的交换机类型以及他们的区别
RabbitMQ中有四种主要的交换机类型,它们是:Direct,Topic,Fanout,Headers。 Direct(直连交换机):接收到消息后,会将消息发送到与消息的routing key完全匹配的队列上。Dire…...
)
理解不同层的表示(layer representations)
在机器学习和深度学习领域,特别是在处理音频和自然语言处理(NLP)任务时,"层的表示"(layer representations)通常是指神经网络不同层在处理输入数据时生成的特征或嵌入。这些表示捕获了输入数据的…...

原生js访问http获取数据的方法
在原生JavaScript中,直接通过浏览器端的JavaScript访问HTTP接口获取数据通常涉及XMLHttpRequest对象或现代的fetch API。 1. 使用XMLHttpRequest XMLHttpRequest是一个老旧的API,但在某些情况下仍然很有用。以下是一个简单的例子: javascr…...
Windows 2000 Server:安全配置终极指南
"远古技术,仅供娱乐" 💭 前言:Windows 2000 服务器在当时的市场中占据了很大的比例,主要原因包括操作简单和易于管理,但也经常因为安全性问题受到谴责,Windows 2000 的安全性真的那么差吗&#x…...

基于 FastAI 文本迁移学习的情感分类(93%+Accuracy)
前言 系列专栏:【深度学习:算法项目实战】✨︎ 涉及医疗健康、财经金融、商业零售、食品饮料、运动健身、交通运输、环境科学、社交媒体以及文本和图像处理等诸多领域,讨论了各种复杂的深度神经网络思想,如卷积神经网络、循环神经网络、生成对抗网络、门控循环单元、长短期记…...
集成Google Authenticator实现多因素认证(MFA)
目录 参考1、应用背景2、多因素认证3、谷歌google authenticator集成用法3.1、原理3.2、 MFA绑定3.2.1、 用户输入用户名密码登录3.2.2、检查是否已经绑定MFA(检查数据库是否保存该用户的google secret)3.2.3、谷歌身份证认证器扫描绑定3.2.4、手动测试验…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...
