2005NOIP普及组真题 3. 采药
线上OJ:
[05NOIP普及组] 采药
核心思想:
1、题与 2006 年普及组第2题《开心的金明》一样,考察的都是01背包。
2、直接套用01背包的一阶模板即可
a、限定时间看成背包总容量m
b、每件物品的采药时间 v 看成占用背包的体积
c、每件物品的价格w作为该物品的价值
则本题可套用标准的01背包问题模板:
for(int i = 0; i < n; i++) // n个物品供选择
{int v, w;scanf("%d %d", &v, &w); // 每个物品的体积v, 价值wfor(int j = m; j >= v; j--) f[j] = max(f[j], f[j - v] + w); // 从总容量m->当前物品读入的体积v, 逆序计算f[j]
}
题解代码:
#include <bits/stdc++.h>
using namespace std;const int N = 1010;int n, m;
int f[N];int main()
{scanf("%d%d", &m, &n);for (int i = 0; i < n; i ++ ){int v, w;scanf("%d%d", &v, &w);for (int j = m; j >= v; j -- ) f[j] = max(f[j], f[j - v] + w);}printf("%d\n", f[m]); return 0;
}
相关文章:

2005NOIP普及组真题 3. 采药
线上OJ: [05NOIP普及组] 采药 核心思想: 1、题与 2006 年普及组第2题《开心的金明》一样,考察的都是01背包。 2、直接套用01背包的一阶模板即可 a、限定时间看成背包总容量m b、每件物品的采药时间 v 看成占用背包的体积 c、每件物品的价格w作为该物品的…...
与stopPropagation()有什么区别?)
preventDefault()与stopPropagation()有什么区别?
1、event.preventDefault()方法 (1)可防止元素的默认行为 (2)如果在表单元素中使用,它将阻止其提交 (3)如果在锚元素中使用,它将阻止其导航 (4)如果在上下…...

AIGC 全面介绍
随着人工智能技术的不断进步,生成式人工智能(AI Generated Content, AIGC)成为了一个日益热门的话题。AIGC 指利用人工智能技术生成各类内容,包括文本、图像、音频、视频等。与传统的内容生成方法相比,AIGC 具有速度快…...
网站入门:Flask用法讲解
Flask是一个使用Python编写的轻量级Web服务框架,旨在帮助开发人员快速构建和部署Web应用程序。下面将对Flask进行更为详细的解释说明,并展示其使用示例与注意事项: 1.解释说明 定义及特点: Flask以其简洁和灵活著称,允许开发者以…...

头歌数据库备份与恢复
第1关:数据库的备份和恢复 mysql -uroot -p123123 -h127.0.0.1 < /data/workspace/myshixun/src/data.sqlmysqldump -u root -p studb student> /student_bk.sqlmysql -uroot -p123123 -h127.0.0.1 -e "create database studb2;"mysql -u root -p123123 studb…...
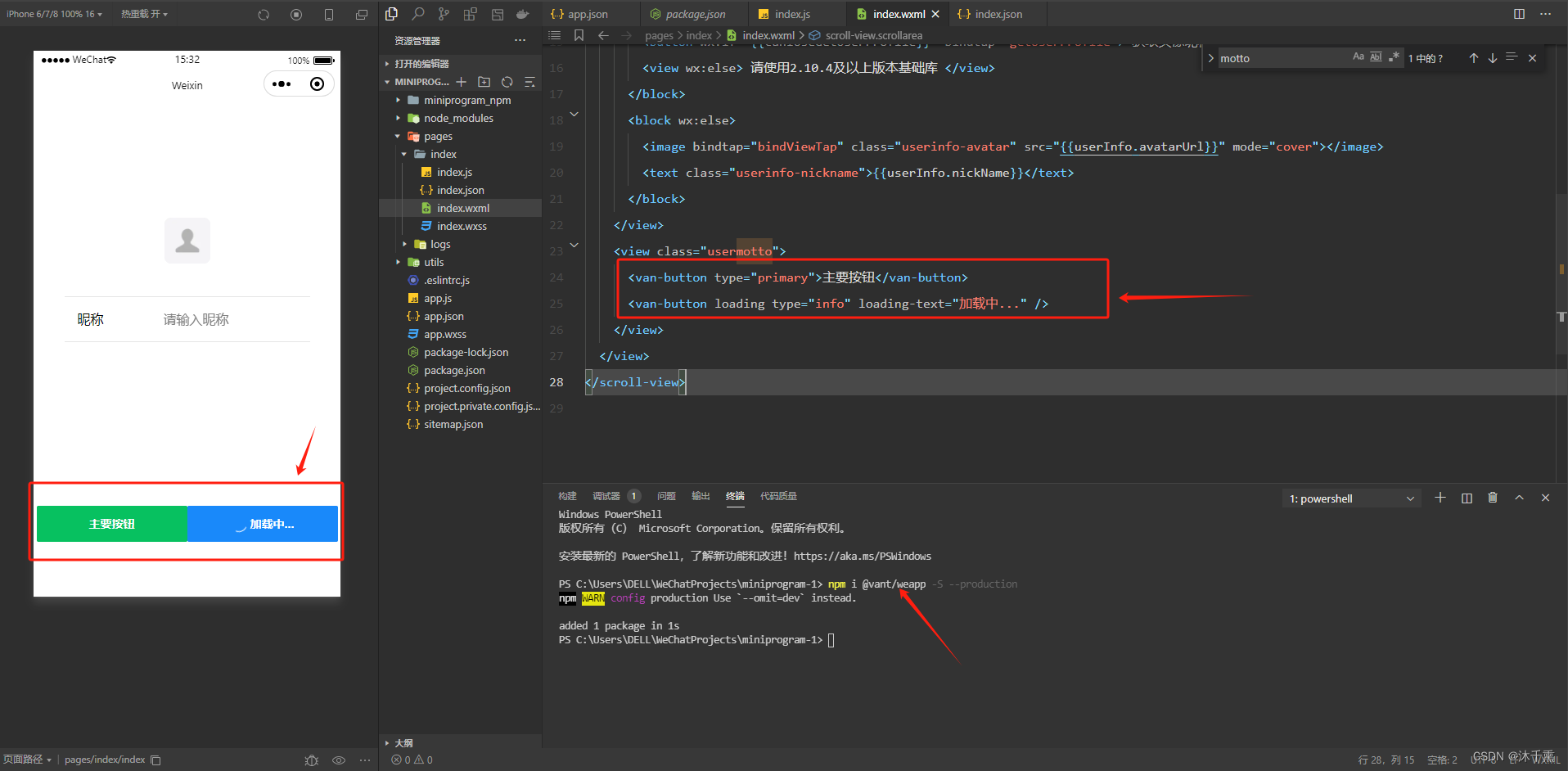
小程序项目创建与Vant-UI引入
一,创建小程序项目 AppID可先用测试号; 模板来源选择 ’全部来源‘ ,’基础‘ 。模板一定JS开头的; vant-weapp 官网 vant-Weapp 二,下载vant-weapp 组件 1,在新项目中打开 ’调试器‘; 2…...

xtrabackup 使用
官网 Percona XtraBackup Use APT repositories - Percona XtraBackup 一 安装 下载 wget https://repo.percona.com/apt/percona-release_latest.$(lsb_release -sc)_all.deb wget https://repo.percona.com/apt/percona-release_latest.zesty_all.deb 可下载列表 Perc…...

C++写一个简单的计算器程序案例
1. 编写C源代码 创建一个名为 advanced_calculator.cpp 的文件,并编写以下代码: // advanced_calculator.cpp #include <iostream> #include <limits>int main() {char operatorChoice;bool keepRunning true;while (keepRunning) {int nu…...

Spring Boot 开发 -- swagger3.0 集成
前言 随着微服务架构的普及和API数量的增长,API文档的管理和维护变得尤为重要。Swagger作为一款强大的API文档生成工具,能够帮助我们自动生成API文档,并提供在线测试功能,极大地提高了开发效率。本文将介绍如何在Spring Boot项目…...

探索安全之道 | 企业漏洞管理:从理念到行动
如今,网络安全已经成为了企业管理中不可或缺的一部分,而漏洞管理则是网络安全的重中之重。那么企业应该如何做好漏洞管理呢?不妨从业界标准到企业实践来一探究竟!通过对业界标准的深入了解,企业可以建立起完善的漏洞管…...

【记录贴:分布式系列文章】
分布式系列文章目录 文章目录 分布式系列文章目录前言一、Redisq1.怎么判断是否命中缓存1. MySQL数据库如何检查询查缓存是否命中链接2.如何判断redis是否命中缓存链接 q2.Redis缓存穿透、雪崩、击穿以及分布式锁和本地锁 二、分布式q1.分布式订单号生成策略q2.接口幂等性,防止…...
)
初识SDN(二)
初识SDN(二) SDN部分实现 REST API 是什么? REST API(Representational State Transfer Application Programming Interface,表述性状态传递应用程序接口)是一种基于HTTP协议的接口,广泛用于…...

某红书旋转滑块验证码分析与协议算法实现(高通过率)
文章目录 1. 写在前面2. 接口分析3. 验证轨迹4. 算法还原 【🏠作者主页】:吴秋霖 【💼作者介绍】:擅长爬虫与JS加密逆向分析!Python领域优质创作者、CSDN博客专家、阿里云博客专家、华为云享专家。一路走来长期坚守并致…...
Gin的快速入门和搭建
文章目录 Go的工程工程架构技术选型 Gin入门 Go的工程 基于Go生态,构建一个支持内容管理,内容加工、内容分发的内容库系统。 内容管理:增删改查内容加工:例如内容审核、推荐等内容分发:将内容可以推到不同的业务线 …...
react-native运行程序 出现 Application XXX is waiting for the debugger
1.重启adb: adb kill-server、 adb start-server. 2、确定USB调试模式是否开启,如果已经开启了,关闭了重新打开一下 3.选择调试模式并关闭等待调试程序...

什么文档加密软件好用?迅软DSE加密软件你不会还不知道吧?
一、什么文档加密软件好用? 其中有迅软DSE文档加密软件等。 迅软DSE加密软件:让企业的创意成果、招投标文件、生产工艺、流程配方、研发成果、公司计划、员工信息等核心数据更安全。 多方面加密模式,有效防止数据泄密 透明无感知加密&…...

【kubernetes】关于k8s集群的污点、容忍、驱逐以及k8s集群故障排查思路
目录 一、污点(Taint) 1.1污点介绍 1.2污点的组成格式 1.3当前 taint effect 支持如下三个选项: 1.4污点的增删改查 1.4.1验证污点的作用——NoExecute 1.4.2验证污点的作用——NoSchedule 1.4.3 验证污点的作用——PreferNoSchedule 1.5污点的配置与管理…...

linux进程加载和启动过程分析
我们的源代码通过预处理,编译,汇编,链接后形成可执行文件,那么当我们在终端敲下指令$ ./a.out argv1 argv2 后,操作系统是怎么将我们的可执行文件加载并运行的呢? 首先知道,计算机的操作系统的启动程序是写死在硬件上的,每次计算机上电时,都将自动加载启动程序,之后…...
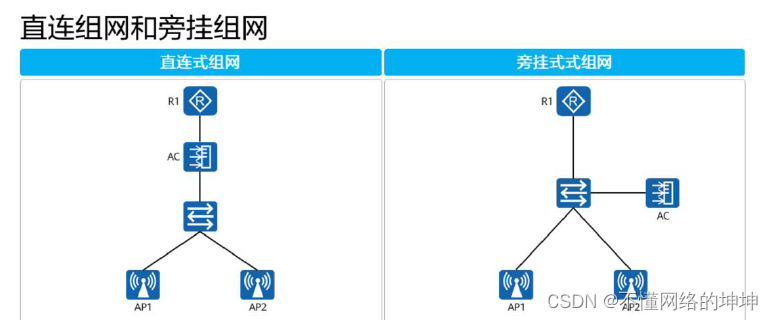
WLAN组网模型探究
目录 一、WLAN基本概念二、WLAN组网方式三、WLAN转发模型 随着信息技术的飞速发展,无线局域网(WLAN)已逐渐成为企业网络架构中不可或缺的一部分。不同的企业组织因其业务特性、规模大小及安全需求的不同,对WLAN的要求也各有侧重。…...

操作系统基础知识
一. 进程 进程是正在运行中的程序,是动态的 进程是资源分配的最小单位 进程的基本特征:动态性,并发性,独立性,异步性 二. 线程 线程在执行过程中的每一个任务就是一个线程 进程是由一个或多个线程组成࿰…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

数据结构:泰勒展开式:霍纳法则(Horner‘s Rule)
目录 🔍 若用递归计算每一项,会发生什么? Horners Rule(霍纳法则) 第一步:我们从最原始的泰勒公式出发 第二步:从形式上重新观察展开式 🌟 第三步:引出霍纳法则&…...
