数据结构：泰勒展开式：霍纳法则（Horner‘s Rule）

目录

🔍 若用递归计算每一项，会发生什么？

Horner's Rule（霍纳法则）

 第一步：我们从最原始的泰勒公式出发

第二步：从形式上重新观察展开式 

🌟 第三步：引出霍纳法则（Horner’s Rule）

 第四步：如何用这个结构重写泰勒展开式？ 

完整代码

 从迭代转换成递归逻辑

“迭代”和“循环” 

---

当前递归方法的结构回顾：

double num = 1, den = 1;double taylor(int n, double x) {if (n == 0) return 1;double res = taylor(n - 1, x);  // 一次函数调用num *= x;                       // 分子：一次乘法den *= n;                       // 分母：一次乘法return res + num / den;
}

这一版已经做了初步优化：我们通过 累计 num 和 den 来避免重复调用 pow(x,n) 和 factorial(n)。

但这只是相对优化，我们现在要分析：

🔍 若用递归计算每一项，会发生什么？

我们从第 0 项到第 n 项共计算 n+1项，每一项的乘法成本如下：

第 k 项	乘法次数
k = 0	0
k = 1	1
k = 2	2
...	...
k = n	n

所以总乘法次数为：

✅ 因此，乘法总次数为 O(n^2）！

🚨 问题在哪里？

• 你对每一项都重新计算幂和阶乘

• 导致重复计算，浪费大量 CPU 时间

• 如果你希望 n = 50、n = 100，程序变慢得很明显

🤔 有没有更好的方式？

是的。你就引出了今天的主角：

Horner's Rule（霍纳法则）

我们可以尝试换一种展开方式，让我们不必每次都分别去计算幂和阶乘。

我们将展开式进行重写：

也就是一种嵌套式计算结构。

这个就是 Horner 法则的思路 —— 逐层乘进去、逐层加出来，避免重复乘法和幂展开。

---

 第一步：我们从最原始的泰勒公式出发

以 e^x 为例，泰勒展开是：

 

这表达得很清晰，每一项结构都类似：

• 分子是 x^k

• 分母是 k！

所以直觉上，我们就写了：

double num = 1;  // 分子
double den = 1;  // 分母double taylor(int n, double x) {if (n == 0) return 1;               // 1️⃣ 锚点：停止递归double res = taylor(n - 1, x);      // 2️⃣ 先构造前面所有项的和num *= x;                           // 3️⃣ 然后再更新状态den *= n;return res + num / den;             // 4️⃣ 当前项加进去
}

 递归方法的思路解析，可以看我之前发表的文章：

数据结构：递归：泰勒展开式（Taylor Series Expansion）-CSDN博客

 但是整个算法需要 O(n^2) 次的乘法。

于是我们问自己：

❓有没有一种办法，我们不显式地计算幂和阶乘，而是用一种更聪明的方式重写它？

第二步：从形式上重新观察展开式 

我们把：

我们尝试反向收敛：

从最后一项往前看。 

设：

假设我们已知最后一项是：

我们问：有没有可能构造出一个结构：

 

我们知道这种结构是逐层“乘进去再加”，是一种“嵌套结构”。

这时候，你会自然联想到：

---

🌟 第三步：引出霍纳法则（Horner’s Rule）

Horner's Rule 是一种重写多项式的方式，使其变成嵌套乘加结构，从而节省乘法次数。

给你一个多项式：

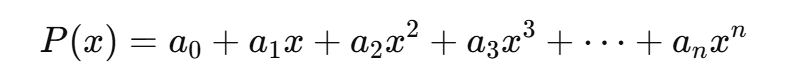
它可以等价重写成：

 

第一步：从最后一项开始反向思考 

先写出最后一项：

但我们不这么直接展开，而是尝试合并每一项，构建嵌套结构。我们回顾一下： 

第二步：尝试因式提取，构造嵌套结构 

我们从最后一项往回包，先只保留最后一项：

向前一项加：

 再加：

 最后加 1 项：

第三步：得出结论（形式）

最终你得到的就是：

 

这就是 Horner 法则在泰勒展开中的精确结构！ 

 

---

 第四步：如何用这个结构重写泰勒展开式？ 

霍纳法则告诉我们：

如果你有一个嵌套表达式，它从最深处开始乘加，就可以从最后一项反向累积计算。

我们的目标是以某种结构计算它，让乘法次数最少。 

观察这个嵌套结构你会发现：

• 每一层都包含一个 “1 + x / k * (之前的结果)”

• 最里面的是 1

• 然后不断被 x/k 包裹

它是一个“逐层包裹”的结构，每一层是：

 这说明我们可以从“最深的那一层”开始往外展开。

于是你意识到这就是一种“右折叠（right fold）”，即：

result = 1;
result = 1 + x * result / 4;
result = 1 + x * result / 3;
result = 1 + x * result / 2;
result = 1 + x * result / 1;

 从后往前包，每次乘进去一个 x / i，再加 1。

所谓「右折叠」就是我们从表达式的最右边开始构建，逐层包起来。 

1 + x/4              ← 第 1 层（最里面）
1 + x/3 * (1 + x/4)  ← 第 2 层
1 + x/2 * (...)      ← 第 3 层
1 + x/1 * (...)      ← 第 4 层

你看到一种非常明显的重复：

每次的操作是：

result = 1 + x * result / i;

从哪个 i 开始？

• 最深一层是对应最大项 n

• 然后是 n - 1

• 最后是 i = 1

所以你会写一个反向的循环：

for (int i = n; i > 0; --i)

初始值设置为：

double result = 1.0;  // 最里层的恒定值

为什么是 1.0？

因为你可以认为最内层就是 1 + 0，也就是我们从最后一项 x^n / n! 折叠得到的值是最深的那个 1，逐层向外构建。

完整代码

double horner_taylor(int n, double x) {double result = 1.0;                  // 最深嵌套项for (; n > 0; n--) {                 // 从内往外迭代result = 1 + x * result / n;     // 每次构造一层}return result;
}

---

 从迭代转换成递归逻辑

递归的本质是：

用一个函数在每一层调用自己，把循环变成函数调用链。

从上面的迭代式：

你可以直接转换成递归表达式：

double horner_recursive(int n, double x) {static double result = 1.0;if (n == 0) return result;       // 最深嵌套项（base case）result = 1 + x / n * result;  return horner_recursive(n - 1, x);   
}

循环版结构	递归版结构
从 n 逐步降到 1	从 n 递归到 0（递归终止条件）
每次更新 result = ...	每次返回 1 + x * 下层 / n
初始 result = 1.0	horner_recursive(0, x) = 1.0

两者实际上是完全等价的计算结构。

---

“迭代”和“循环” 

什么是“循环”（loop）？

• 循环是语法结构

• 是编程语言提供的控制流语句（for、while、do-while）

• 它的作用是：重复执行某段代码

比如：

for (int i = 0; i < 10; ++i) {// 执行 10 次
}

什么是“迭代”（iteration）？

• 迭代是算法行为

• 意思是：基于前一个结果，不断构造下一个结果

• 它不依赖一定要用循环语法，也可以用递归实现！

举例说明：

✅ 迭代行为 + 循环实现

double result = 1;
for (int i = n; i > 0; --i)result = 1 + x * result / i;

• 每一轮基于上一轮的 result

• 所以这是一个迭代算法

• 同时用了 for，所以也是一个循环结构

 ✅ 迭代行为 + 递归实现

double horner_recursive(int n, double x) {static double result = 1.0;if (n == 0) return result;       // 最深嵌套项（base case）result = 1 + x / n * result;  return horner_recursive(n - 1, x);   
}

• 每一层基于“下一层”的结果

• 所以也是一种迭代算法

• 但这次用的是递归结构

 🚫 循环 ≠ 迭代（反例）

for (int i = 0; i < 10; ++i) {cout << "Hello\n";
}

• 这使用了循环，但没有迭代行为（没有前后状态依赖）

• 所以它是循环，但不是迭代