2024089期传足14场胜负前瞻
2024089期售止时间为6月3日(周一)22点00分,敬请留意:

本期1.5以下赔率5场,1.5-2.0赔率5场,其他场次是平半盘、平盘。本期14场难度偏低。以下为基础盘前瞻,大家可根据自身判断,复选增加防单。

1、克罗地亚 VS 北马其顿
克罗地亚在近四场各项赛事中,取得了三胜一平的不败战绩,显示出其稳定的竞技状态。而实力较弱的北马其顿,在近四场各项赛事中仅取得两平两负的战绩,未能取得一胜。相较于北马其顿,克罗地亚在本场比赛中有望轻松取得胜利。
2、英格兰 VS 波黑
英格兰队在今年与巴西和比利时的交锋中均未能找到破门制胜的契机,队伍内部弥漫着浓厚的挫败感与怨气,球员们迫切希望释放压力。波斯尼亚队的实力较为有限,其在欧洲国际分组赛中更是位列小组倒数第二,表现不尽如人意。英格兰队在本场比赛中有望取得今年的首场胜利,展现其强大的竞技实力。
3、德国 VS 乌克兰
德国在今年的一系列友谊赛中,先后战胜了法国和荷兰,这无疑为球队中的将士们注入了巨大的信心。此次面对实力稍逊一筹的乌克兰,德国队有望取得一场大胜。

4、罗马尼亚 VS 保加利亚
保加利亚队目前保持不败战绩,然而其胜场数量较少,影响了其整体表现的含金量。罗马尼亚队近期表现出现下滑趋势,显示出不稳定。鉴于双方目前的状态和实力对比,预计此次相遇将难以产生激烈对抗,而是以平局收场。
5、奥地利 VS 塞尔维亚
奥地利队表现卓越,连续五场比赛取得胜利,展现出极佳的竞技状态。在此期间,球队进攻端火力全开,共计攻入11球,展现出强大的攻击力。因此,本场比赛奥地利队有望轻松取得大胜。
6、爱尔兰 VS 匈牙利
匈牙利近期表现强势,连续多场比赛保持不败,目前更是取得了三连胜的佳绩。而对手爱尔兰则陷入了低谷,近四场比赛均未能取得胜利。在本场比赛中,匈牙利队目标明确,志在取得胜利,继续巩固其不败战绩。

7、葡萄牙 VS 芬兰
两队在实力上存在显著差距,葡萄牙队在国际足坛排名高居第六,而芬兰队则远在世界排名六十之外。加之葡萄牙队近期整体表现更为出色,对于本场比赛,我们更倾向于葡萄牙队能够取得胜利。
8、意大利 VS 土耳其
在过去的两次交锋中,意大利均成功战胜了土耳其,展现出了明显的竞技优势。从近期表现来看,意大利的发挥也明显优于土耳其。在此次再度相遇的情况下,意大利无疑值得人们寄予厚望。
9、丹麦 VS 瑞典
今年双方进行的友谊赛中,均取得过胜利场次,彼此实力相当,无显著差距。两队在即将进行的比赛中,握手言和的可能较大。

10、挪威 VS 科索沃
挪威近期在与具备欧国盃正赛资格的斯洛伐克交锋中,依旧保持不败战绩,展现出强大的竞技实力。相较之下,科索沃此前在与匈牙利的比赛中失利,形势略显不利。在此消彼长的情况下,挪威在本场比赛中的胜算显然更大,值得优先考虑。
11、比利时 VS 黑山
比利时国家队汇聚了多名效力于欧洲五大联赛的主力球员,整体实力远超黑山队,本场比赛比利时取胜可谓轻而易举,无需费过多周折。
12、法国 VS 卢森堡
法国作为欧洲杯夺冠的有力竞争者之一,在近一场热身赛中成功取得胜利。本场比赛,法国将迎战实力远逊于自身的卢森堡队,预计法国将大比分战胜对手。

13、西班牙 VS 安道尔
西班牙在与传统劲旅巴西的较量中,单场攻入对手三球,展现出了球队进攻端的出色实力。此番迎战实力较弱的安道尔,西班牙必将全力以赴,力争取得胜利,重回胜利轨道。
14、瓦奇巴托 VS 格雷米奥
瓦奇巴托表现出色,连续取得两场胜利,且场均进球数超过两球。此次对阵曾经的手下败将格雷米奥,瓦奇巴托有望再次取得胜利,延续其连胜势头。
编辑:大彩虹足球(dacaihong168)
相关文章:

2024089期传足14场胜负前瞻
2024089期售止时间为6月3日(周一)22点00分,敬请留意: 本期1.5以下赔率5场,1.5-2.0赔率5场,其他场次是平半盘、平盘。本期14场难度偏低。以下为基础盘前瞻,大家可根据自身判断,复选增…...
备战十一届大唐杯国赛预选赛
这次省赛带了太多个省一了,具体可看下面的图片,只放了一部分。目前根据可靠消息,应该还有个预选赛和去年一样,就是还会考一次仿真。如果说通过了就是国二起步然后去北方工业争夺国一国二,没过的话就是国三。 每…...

安装 Android Studio 2024.1.1.6(Koala SDK35)和过程问题解决
记录更新Android Studio版本及适配Android V应用配置的一些过程问题。 安装包:android-studio-2024.1.1.6-windows.exe原版本:Android Studio23.2.1.23 Koala 安装过程 Uninstall old version 不会删除原本配置(左下角提示) Un…...
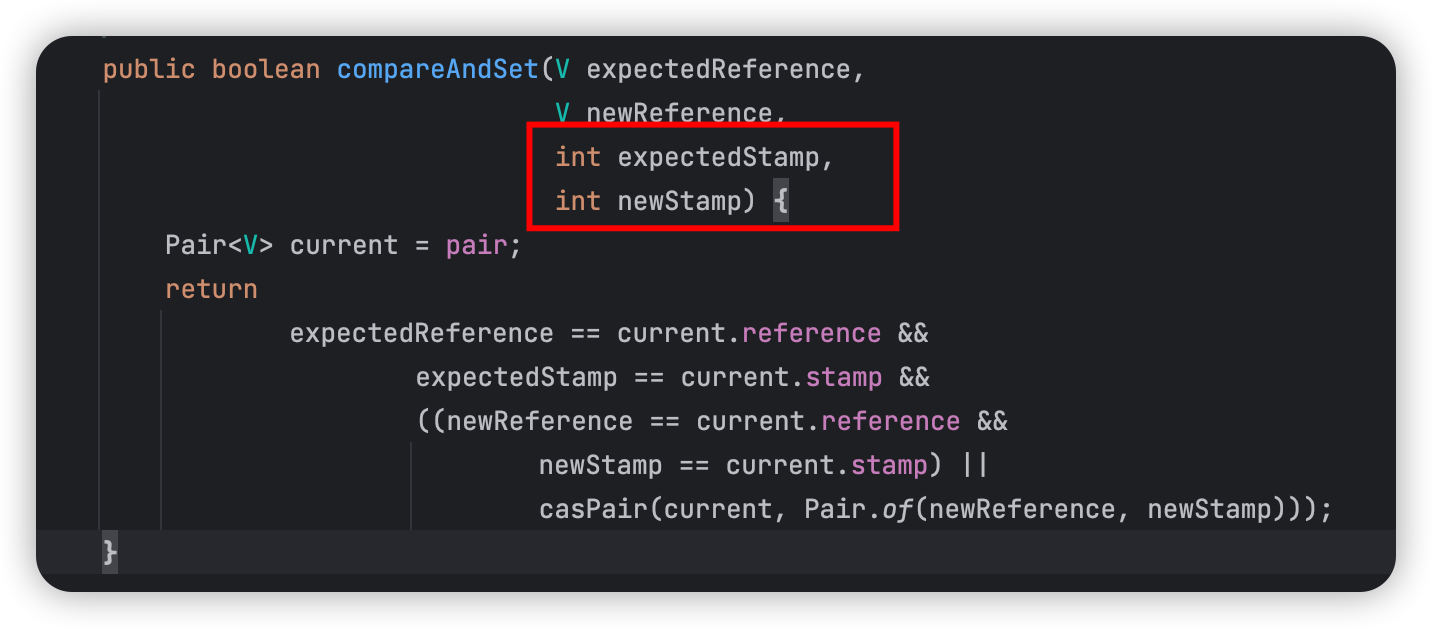
美团一面:什么是CAS?有什么优缺点?我说你说的是AtomicInteger吗?
引言 传统的并发控制手段,如使用synchronized关键字或者ReentrantLock等互斥锁机制,虽然能够有效防止资源的竞争冲突,但也可能带来额外的性能开销,如上下文切换、锁竞争导致的线程阻塞等。而此时就出现了一种乐观锁的策略&#x…...
文件内容排序sort)
【linux】(2)文件内容排序sort
sort 是一个用于排序文件内容的命令行工具,在 Linux 和 Unix 系统中非常常用。 基本用法 sort [OPTION]... [FILE]...常用选项 按数值排序 -n sort -n filename例子:对包含数值的文件进行排序。 按字典顺序排序 -d sort -d filename例子࿱…...

css 图片上添加模糊背景的文字内容
html部分 <div class"onlogo"> <img src"../assets/img/banner.png" /><div class"imgText"><div class"title">一体化电子印章应用服务</div><div class"content">为企业提供安全可靠…...

Python3 函数参数
前言 本文主要介绍python中的函数参数,主要内容包括形式参数与实际参数的概念、位置参数、关键字参数、默认参数、可变参数。 文章目录 前言一、形式参数与实际参数的概念二、位置参数(也叫必需参数)三、关键字参数四、默认参数五、可变参数…...

精准检测,可燃气体报警系统的技术原理与特点
在现代化的工业生产与日常生活中,可燃气体泄露事故频发,给人们的生命和财产安全带来了严重威胁。 因此,可燃气体报警检测系统的应用变得尤为重要。它不仅能够实时监测环境中的可燃气体浓度,还能在发现异常情况时及时报警…...

6月2(信息差)
🌍特斯拉:Model3高性能版预计6月中旬开启首批交付 🎄微软对开源字体 Cascadia Code 进行重大更新 ✨天猫618加码引爆消费热潮 截至晚9点185个品牌成交破亿 1.瑞士清洁科技公司Librec开发废旧锂离子电池回收技术,可回收电池90%的…...
先锋文汇发稿技巧方法
v:yangwei013049 看到标题,有的同志也许会说,投稿就是把稿子发走就行了呗,这要讲究什么方法呢?其实,投稿里面也有学问。不会投稿,方法不当,往往得不到好的效果。 从我多年的实践和…...
无人机推流/RTMP视频推拉流EasyDSS无法卸载软件是什么原因?
视频推拉流/直播点播EasyDSS平台支持音视频采集、视频推拉流、播放H.265编码视频、存储、分发等视频能力服务,在应用场景中可实现视频直播、点播、转码、管理、录像、检索、时移回看等。此外,平台还支持用户自行上传视频文件,也可将上传的点播…...

QML信号连接到c++的槽函数(五)
文章目录 前言一、QML Signal and Handler Event System二、QML信号连接到c++的槽函数代码实例1. 创建一个QML 工程2. 用C++ 实现一个QML Types3. 代码实例4. 运行结果总结参考资料前言 本文主要介绍,如何将QML 中的信号连接到C++ 中的槽函数 软硬件环境: 硬件:PC 软件:wi…...
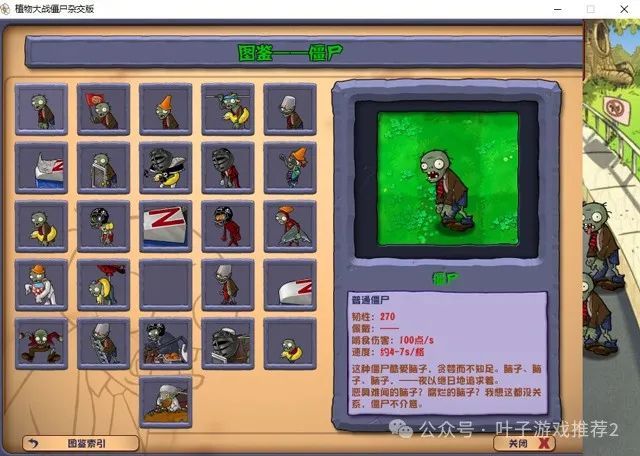
[Windows] 植物大战僵尸杂交版
游戏包含冒险模式、挑战模式、生存模式三种不同玩法。冒险模式主打关卡闯关,挑战模式则挑战特殊设计的关卡,生存模式结合无尽模式和特殊地图,各具特色。玩家可根据喜好自由选择模式,体验不同的游戏乐趣。快来尝试这款独特的pvz游戏…...

JVM之【GC-可达性分析算法】
在Java虚拟机(JVM)中,可达性分析算法(Reachability Analysis)用于垃圾收集,以确定哪些对象是“可达”的,即哪些对象仍然有用,哪些对象可以被回收。下面是对可达性分析算法及其底层实…...

【机器学习】——驱动智能制造的青春力量,优化生产、预见故障、提升质量
目录 一.优化生产流程 1.1 数据收集 1.2 数据预处理 1.3 模型训练 1.4 优化建议 1.5 示例代码 二.预测设备故障 2.1 数据收集 2.2 数据预处理 2.3 模型训练 2.4 故障预测 2.5 示例代码 三.提升产品质量 3.1 数据收集 3.2 数据预处理 3.3 模型训练 3.4 质量提升…...
Python实用代码片段分享(三)
在今天的博文中,我们将继续分享一些Python编程中非常实用的代码片段。这些代码片段将帮助你更高效地处理常见任务,从字符转换到数据类型检查,应有尽有。 1. ord函数和chr函数 Python的ord()函数可以返回Unicode字符对应的ASCII码值…...

树形结构-CRUD接口
先看一下效果:整体的效果 新增效果 --默认值是 default 修改效果 - 大致效果如上 --------------------------------------------------------------------------------------------------------------------------------- 下面讲解代码如何实现的 根据你使用…...
【Qt知识】Qt窗口坐标系
Qt的窗口坐标体系遵循标准的计算机图形坐标系统规则 Qt窗口坐标体系特点 坐标原点:窗口坐标体系的原点位于窗口的左上角,即坐标(0, 0)位置。 轴方向: X轴:向右为正方向,随着X坐标值的增加,元素在窗口中从…...
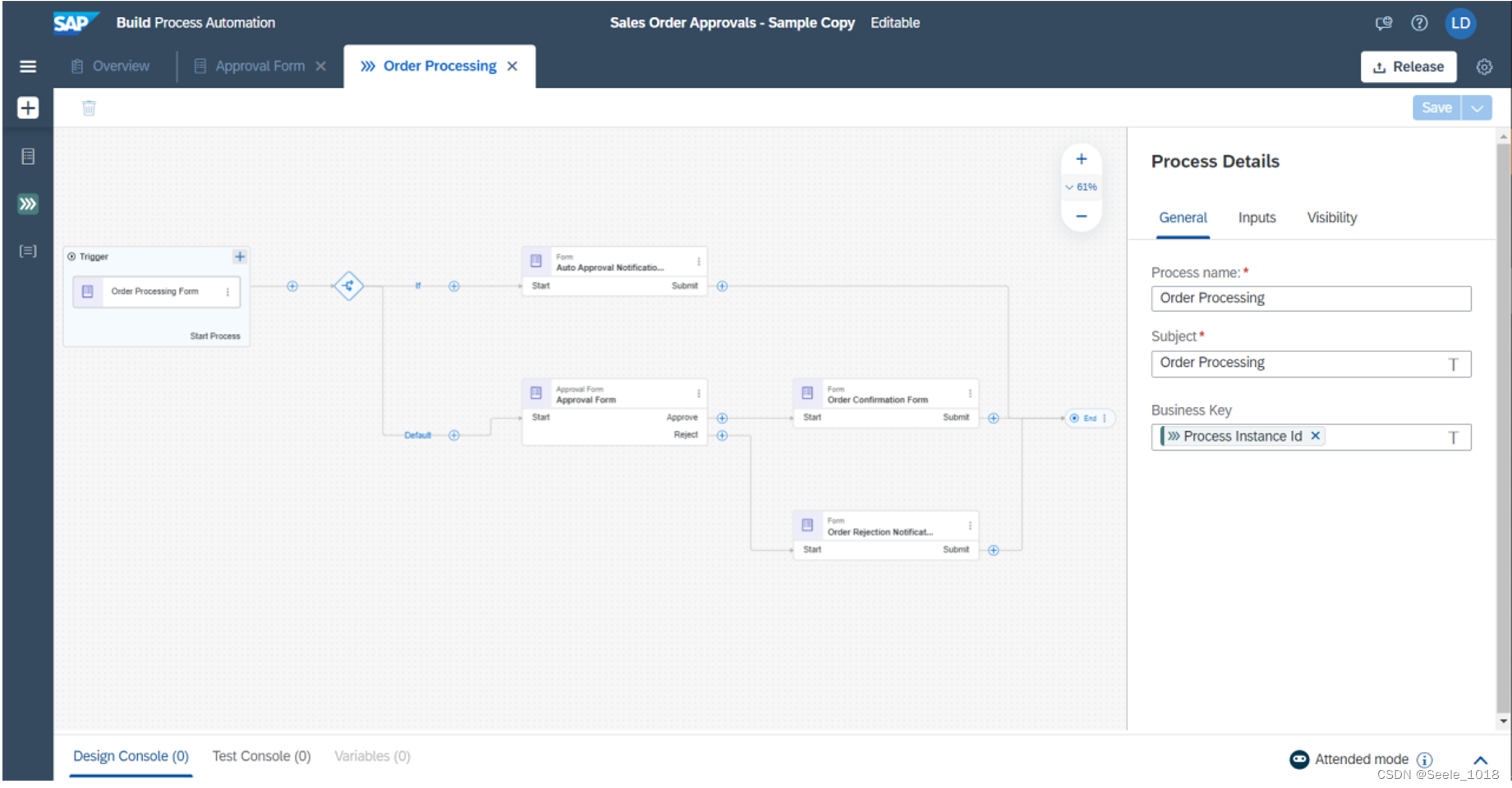
SAP Build引言
前言 SAP Build 似乎是一个整合了很多低代码或无代码产品的平台,最早的时候应该都是各自分开的几个产品,近年合并到一块上了SAP Build平台 现在看官网的介绍应该是有三四个产品被集成进来了,分别是SAP IRPA,SAP Workflow…...

2024上海国际钢丝绳及吊索具展览会
2024上海国际钢丝绳及吊索具展览会 2024 Shanghai International Wire Rope and Hanger Exhibition 时间:2024年12月18日--20日 地点:上海新国际博览中心 详询主办方陆先生 I38(前三位) I82I(中间四位ÿ…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...
