深度神经网络——什么是梯度下降?
如果对神经网络的训练有所了解,那么很可能已经听说过“梯度下降”这一术语。梯度下降是提升神经网络性能、降低其误差率的主要技术手段。然而,对于机器学习新手来说,梯度下降的概念可能稍显晦涩。本文旨在帮助您直观理解梯度下降的工作原理。
梯度下降作为一种优化算法,其核心在于通过调整网络的参数来优化性能,目标是最小化网络预测与实际或期望值(即损失)之间的差距。梯度下降从参数的初始值出发,利用基于微积分的计算方法,对参数值进行调整,以提高网络的准确性。虽然理解梯度下降的工作机制并不需要深厚的微积分知识,但了解梯度这一概念是非常必要的。
什么是梯度?
梯度下降是一种通过模拟下山过程来寻找函数最小值的算法。在神经网络的上下文中,这个过程被用来最小化损失函数,即减少网络预测与实际结果之间的差异。
想象一下,损失函数可以被看作是一个多维的地形图,其中包含了神经网络所有可能的权重组合。这张图上的每个点都代表了一个特定的权重设置,而点的高度代表在这个权重设置下的损失值。我们的目标是找到这个地形图中最低的点,也就是损失最小的点。
在这个比喻中:
-
梯度:代表了在这个地形上任何给定点的最快下降方向,也就是指向损失增加最快的方向。梯度本身是一个向量,它的方向是沿着最陡峭的上升路径,而我们想要做的是向相反方向移动,即下山。
-
斜率:梯度的斜率或陡度表示了在特定方向上损失函数增长的速度。斜率越大,表示在这个方向上损失增加得越快。
-
步长:在梯度下降中,步长由学习率决定。学习率是一个超参数,它决定了我们在梯度指示的方向上移动的步长。如果步长太大,我们可能会越过最低点;如果步长太小,收敛到最低点的过程会非常缓慢。
-
迭代更新:在每次迭代中,我们计算当前权重下的梯度,然后根据学习率来更新权重。这个过程重复进行,直到我们到达损失函数的最低点,或者达到其他停止条件。
-
动态调整:随着我们接近最低点,梯度的值(斜率)会减小,这意味着我们可以逐渐减小步长,以更精确地逼近最低点。
梯度的计算通常涉及到损失函数对每个权重的偏导数。这些偏导数告诉我们每个权重对当前损失值的贡献有多大。在实际操作中,我们通常使用自动微分工具来计算这些梯度,这些工具可以高效地为我们提供所需的导数信息。
计算梯度和梯度下降

梯度下降是一种优化算法,它通过迭代过程来调整神经网络中的权重,目的是最小化损失函数,也就是减少预测误差。这个过程可以概括为以下几个步骤:
-
初始化权重:开始时,神经网络的权重是随机初始化的。
-
计算损失:通过前向传播,计算当前权重下的预测值与真实值之间的差异,得到损失值。
-
计算梯度:损失函数关于权重的梯度告诉我们损失增加最快的方向。在梯度下降中,我们需要计算这个梯度,它是一个向量,其元素是损失函数对每个权重的偏导数。
-
更新权重:使用梯度和学习率(alpha)来更新权重。学习率是一个超参数,它决定了我们在梯度指示的方向上移动的步长。更新公式为:
系数 = 系数 − α × delta 系数 = 系数 - \alpha \times \text{delta} 系数=系数−α×delta
其中,delta 是损失函数的梯度,alpha 是学习率。 -
重复迭代:重复步骤2到4,直到满足停止条件,比如损失值减小到一个很小的数值,或者达到预设的迭代次数。
-
收敛:理想情况下,经过足够多次迭代后,权重更新将使损失函数达到一个局部最小值,此时网络参数收敛到最佳配置。
学习率的选择 对于梯度下降的成功至关重要。如果学习率太高,可能会导致跳过最小值点,甚至导致损失函数值增加;如果学习率太低,则会导致收敛速度过慢。通常需要通过实验来找到合适的学习率。
此外,梯度下降有几种变体,如批量梯度下降(Batch Gradient Descent)、随机梯度下降(Stochastic Gradient Descent, SGD)和小批量梯度下降(Mini-batch Gradient Descent),它们在计算效率和内存使用方面有所不同。
梯度下降的类型
梯度下降算法有几种变体,每种都具有不同的特点和适用场景。以下是三种主要的梯度下降方法:
批量梯度下降(Batch Gradient Descent)
批量梯度下降在更新权重之前会遍历所有的训练样本。这种方法的优点是每次更新都是基于整个数据集的损失函数的准确梯度,因此通常可以得到很准确的最小损失估计。然而,由于它需要等待整个数据集处理完毕后才更新权重,所以如果数据集很大,这可能会导致每次更新之间有很长的等待时间,从而减慢学习过程。
随机梯度下降(Stochastic Gradient Descent, SGD)
随机梯度下降每次迭代只处理一个训练样本,并立即更新权重。这种方法的优点是它可以非常快地收敛,因为每次参数更新都是立即进行的。但是,由于每次更新只基于一个样本,这可能会导致更新过程中出现很多噪声,使得收敛的过程不稳定。
小批量梯度下降(Mini-batch Gradient Descent)
小批量梯度下降是批量梯度下降和随机梯度下降的折中方案。它将整个训练数据集分成多个小批量,每次迭代使用一个小批量样本来计算梯度并更新权重。这种方法结合了批量梯度下降的稳定性和随机梯度下降的快速性。小批量梯度下降通常比批量梯度下降收敛得更快,同时也比随机梯度下降更稳定,因此它在实践中非常受欢迎。
选择梯度下降方法
选择哪种梯度下降方法取决于多个因素,包括数据集的大小、计算资源、模型的复杂性以及需要的收敛速度。例如,如果数据集非常大,批量梯度下降可能不太可行,而小批量梯度下降或随机梯度下降可能更合适。如果需要快速原型制作或实时更新,随机梯度下降可能更有优势。而对于需要较高稳定性和精确度的训练任务,小批量梯度下降可能是最佳选择。
每种方法都有其优缺点,理解这些差异有助于在特定问题上选择最合适的梯度下降策略。
Python中实现梯度下降算法
- 定义损失函数:损失函数用于评估模型的预测值与实际值之间的差异。
- 计算梯度:计算损失函数关于模型参数的导数,以确定更新的方向。
- 更新参数:根据梯度和学习率更新模型的参数。
- 迭代优化:重复上述过程直到满足停止条件,如达到预定的迭代次数或损失值低于某个阈值。
以下是一个简单的Python示例,展示了如何使用梯度下降算法来优化一个线性回归模型的参数:
import numpy as np# 假设我们有一些数据
X = np.array([1, 2, 3, 4, 5]).reshape(-1, 1) # 输入特征
y = np.array([2, 4, 6, 8, 10]) # 实际输出# 初始化参数
theta = np.zeros(X.shape[1])# 学习率
alpha = 0.01# 迭代次数
iterations = 1000# 损失函数(均方误差)
def compute_loss(y_true, y_pred):return ((y_true - y_pred) ** 2).mean()# 梯度下降算法
for i in range(iterations):# 预测值y_pred = X.dot(theta)# 计算损失loss = compute_loss(y, y_pred)print(f"Iteration {i+1}, Loss: {loss}")# 计算梯度gradients = -(2/len(X)) * np.dot(X.T, (y - y_pred))# 更新参数theta -= alpha * gradients# 最终参数
print(f"Theta: {theta}")
在这个例子中,我们使用了均方误差作为损失函数,并通过梯度下降更新了模型参数theta。这个例子是一个简单的线性回归问题,其中我们假设模型的参数初始为零,并且我们没有使用任何正则化。
请注意,这个例子是为了演示梯度下降的原理而简化的。在实际应用中,你可能需要考虑更多的因素,如特征缩放、正则化、更复杂的损失函数、动态学习率调整等。此外,对于更复杂的模型(如神经网络),梯度的计算和参数更新通常会使用深度学习框架(如TensorFlow或PyTorch)来实现。
相关文章:

深度神经网络——什么是梯度下降?
如果对神经网络的训练有所了解,那么很可能已经听说过“梯度下降”这一术语。梯度下降是提升神经网络性能、降低其误差率的主要技术手段。然而,对于机器学习新手来说,梯度下降的概念可能稍显晦涩。本文旨在帮助您直观理解梯度下降的工作原理。…...

基本元器件 - 二极管
目录 二极管的主要参数 二极管的分类 整流二极管 快恢复二极管(FRD) 稳压(齐纳)二级管 瞬态电压抑制器(TVS) 开关二极管 肖特基二极管(SBD) 正偏与反偏 常用封装 伏安特性…...
⭐⭐⭐)
【设计模式】单例模式(创建型)⭐⭐⭐
1.概念 1.1 什么是单例模式 单例模式属于创建型模式,一个单例类在任何情况下都只存在一个实例, 构造方法必须是私有的、由自己创建一个静态变量存储实例,对外提供一 个静态公有方法获取实例。 1.2 优点与缺点 优点:是内存中只有一个实例&…...

《深入浅出C语言:从基础到指针的全面指南》
1. 简介 C语言是一种通用的编程语言,广泛应用于系统编程、嵌入式系统和高性能应用程序。它由Dennis Ritchie在1972年开发,并且至今仍然非常流行。C语言以其高效、灵活和强大的功能著称,是许多现代编程语言的基础。 2. 基本语法 2.1 Hello, …...

Typescript高级: 深入实践Record类型
概述 Record 类型是TS中其众多强大特性之一它为我们提供了创建键值对映射的强大能力极大地增强了代码的灵活性与类型安全性 应用示例 1 )用于配置场景 在复杂的项目中,配置文件往往包含多个模块的不同设置使用 Record 可以确保配置的键名正确且值类型…...
)
重构与优化-对象间特性搬移重构(2)
在软件开发过程中,重构是改进代码结构和设计、不改变其外在行为的过程。对象之间的特性搬移(Moving Features Between Objects)是重构的一种重要类型,它涉及到将属性、方法或其他特性从一个对象转移到另一个对象,以优化代码结构、提高可维护性和遵循设计原则。以下是几种典…...

网络流量监控与DNS流量分析
目录 一、网络流量监控的基础知识 什么是网络流量监控? 网络流量监控的重要性 实用案例:如何通过网络流量监控优化带宽利用 二、DNS流量分析的核心要点 什么是DNS流量分析? DNS流量分析的优势 实用技巧:如何通过DNS流量分…...

【数据分析】打造完美数据分析环境:Python开发环境搭建全攻略
打造完美数据分析环境:Python开发环境搭建全攻略 在数据分析的世界中,搭建一个稳定且高效的Python开发环境是至关重要的。本文将介绍三种主要的环境搭建方式:使用pip、Anaconda和Miniconda。 1. 使用pip从清华镜像安装Python包 pip是Pytho…...
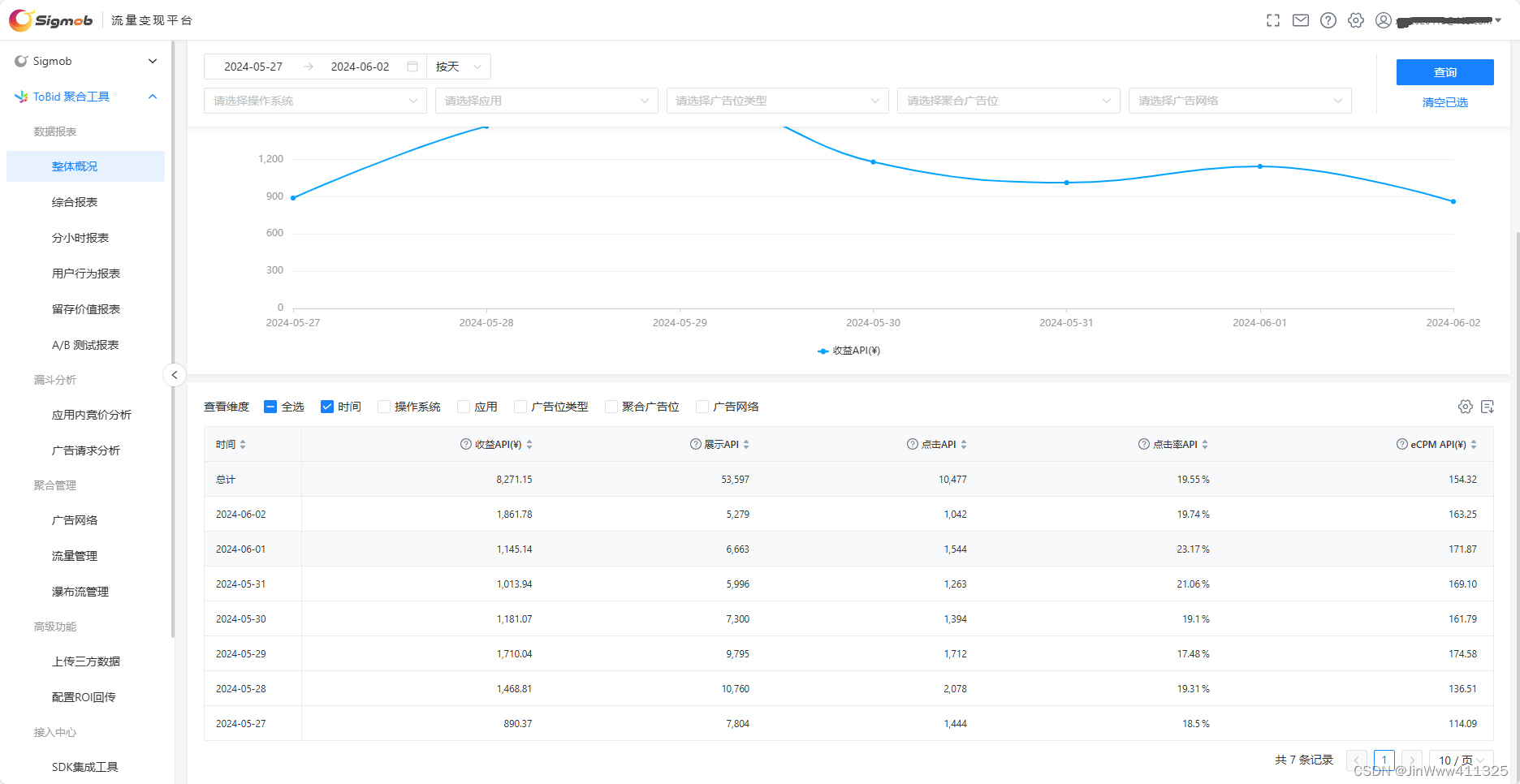
我的app开始养活我了
大家在日常使用各类 app 时应该会发现,进入 app 会有个开屏广告,在使用 app 中,时不时的也会有广告被我们刷到。 这时候如果我们看完了这个广告,或者点击了这个广告的话,app商家就会获得这个广告的佣金。 这个佣金就是…...
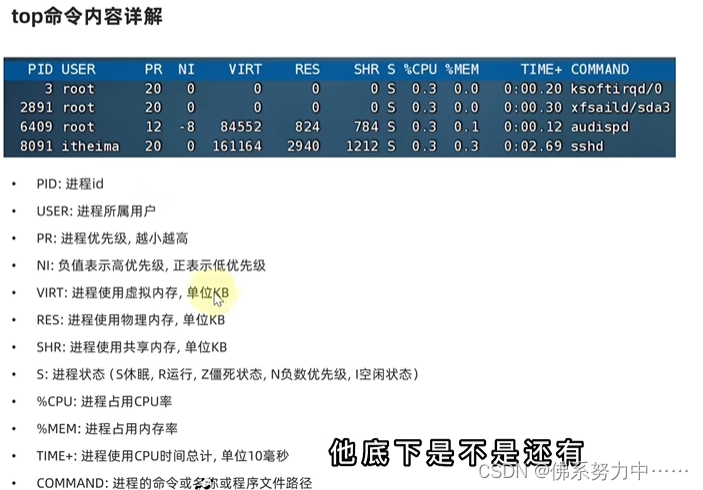
linux中最基础使用的命令
小白学习记录: 前情提要:Linux命令基础格式!查看 ls看目录的小技巧 进入指定目录 cd查看当前工作目录 pwd创建一个新的目录(文件夹) mkdir创建文件 touch查看文件内容 cat、more操作文件、文件夹- 复制 cp- 移动 mv- 删除【危险操作ÿ…...
)
【算法实战】每日一题:17.1 订单处理问题(差分思想,二分搜索)
题目 一个会议中心的场地预订系统。在接下来的 n 天里,会议中心有一定数量的会议室可供租用。共有 m 份预订请求,每份请求描述为 (d_i, a_i, b_i),表示需要从第 a_i 天到第 b_i 天使用会议室(包括第 a_i 天和第 b_i 天࿰…...
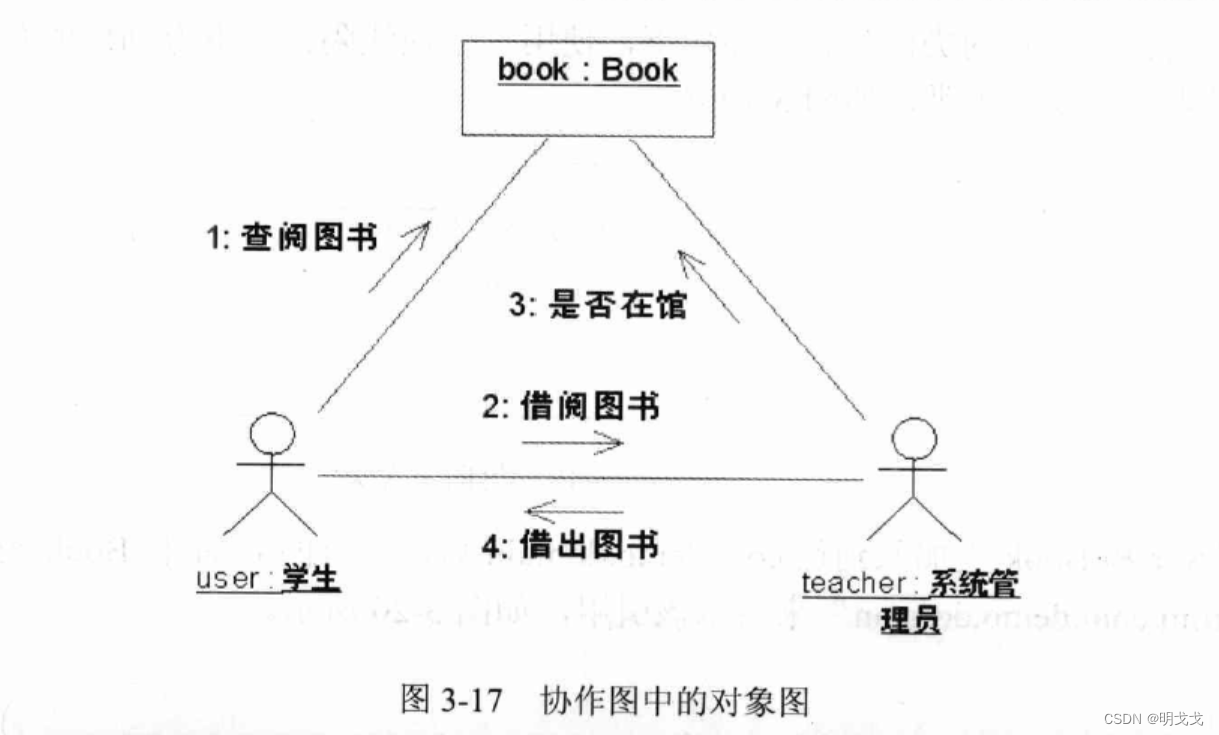
UML静态图-对象图
概述 静态图包含类图、对象图和包图的主要目的是在系统详细设计阶段,帮助系统设计人员以一种可视化的方式来理解系统的内部结构和代码结构,包括类的细节、类的属性和操作、类的依赖关系和调用关系、类的包和包的依赖关系。 对象图与类图之间的关系&…...

数据结构第三篇【链表的相关知识点一及在线OJ习题】
数据结构第三篇【链表的相关知识点一及在线OJ习题】 链表链表的实现链表OJ习题顺序表和链表的区别和联系 本文章主要讲解关于链表的相关知识,喜欢的可以三连喔 😀😃😄😄😊😊🙃&#…...

RabbitMQ-发布/订阅模式
RabbitMQ-默认读、写方式介绍 RabbitMQ-直连交换机(direct)使用方法 目录 1、发布/订阅模式介绍 2、交换机(exchange) 3、fanout交换机的使用方式 3.1 声明交换机 3.2 发送消息到交换机 3.2 扇形交换机发送消息代码 3.2 声明队列,用于接收消息 3.3 binding …...

客运提质增效新模式!苏州金龙客货邮融合公交闪耀2024道路运输展
5月31日,“2024北京国际商用车及零部件展览会”暨“2024北京国际道路客货运输车辆及零部件展览会”(简称为“2024道路运输车辆展”)在中国国际展览中心(顺义馆)落下帷幕。本届展会以“智能、绿色、安全,助力…...

【Python实战】使用postman测试flask api接口
cookie_demo.py # -*- coding: utf-8 -*- """ Time : 2024/5/28 17:14 Author : 娜年花开 File : cookie_demo.py Desc : 需求:用户需要先登陆,登陆之后,通过Cookie来判断是不是能够访问登录后的接口userinfo &quo…...

Docker大学生看了都会系列(二、Mac通过Homebrew安装Docker)
系列文章目录 第一章 Docker介绍 第二章 Mac通过Homebrew安装Docker 文章目录 前言Mac通过Homebrew安装本机环境系统要求terminal命令安装查看安装信息配置阿里云镜像加速登陆阿里云配置加速地址其他国内加速地址 总结 前言 在上一章了解了Docker容器是什么之后,本…...
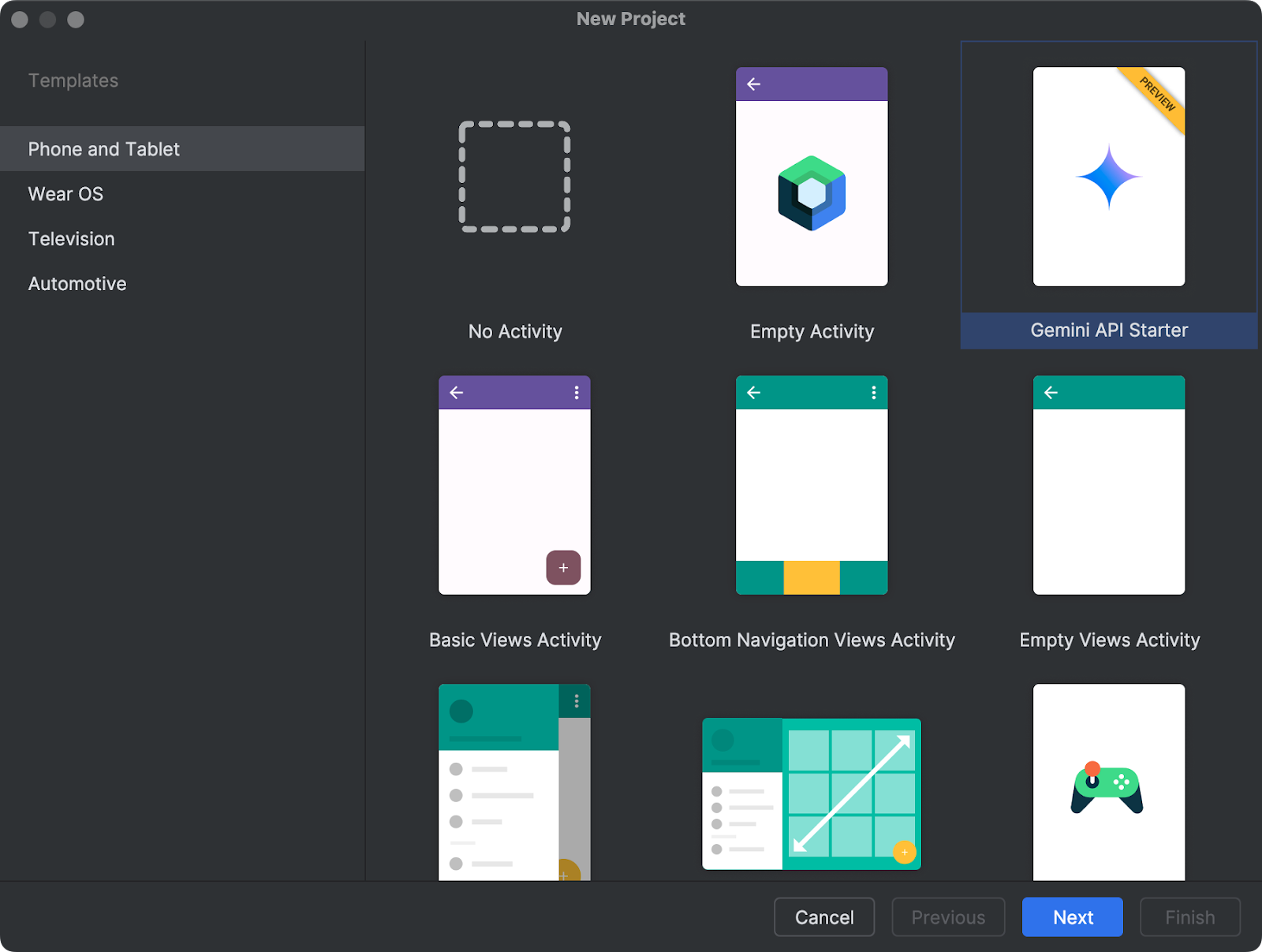
探索 Android Studio 中的 Gemini:加速 Android 开发的新助力
探索 Android Studio 中的 Gemini:加速 Android 开发的新助力 在 Gemini 时代的下一篇章中,Gemini融入了更多产品中,Android Studio 正在使用 Gemini 1.0 Pro 模型,使 Android 开发变得更快、更简单。 Studio Bot 现已更名为 And…...

linux运维——查看网卡实时流量脚本
方法一 以使用iftop命令来查看Linux系统中网卡的实时流量。如果您的系统还没有安装iftop,可以通过包管理器进行安装。 对于基于centos,可以使用以下命令安装: sudo yum install iftop 安装完成后,运行iftop命令查看实时流量&a…...

【三维重建NeRF(三)】Mip-NeRF论文解读
本文结合深蓝学院课程学习和本人的理解,欢迎交流指正 文章目录 Mip-NeRF流程简述混叠问题与MipMapMip-NeRF提出的解决办法圆锥台近似计算与集成位置编码(IPE) Mip-NeRF流程简述 Mip-NeRF的大体流程和NeRF基本是一样的,NeRF介绍 创新的部分就是针对NeRF…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...
