【算法实战】每日一题:17.1 订单处理问题(差分思想,二分搜索)
题目
一个会议中心的场地预订系统。在接下来的 n 天里,会议中心有一定数量的会议室可供租用。共有 m 份预订请求,每份请求描述为 (d_i, a_i, b_i),表示需要从第 a_i 天到第 b_i 天使用会议室(包括第 a_i 天和第 b_i 天),每天需要使用 d_i 个会议室。预订按照提交时间顺序处理,如果某个请求的需求超出了会议中心剩余的会议室数量,那么需要暂停处理流程,通知当前申请者调整他们的请求。工作人员需要知道是否所有的请求都能被完全满足,如果不能,还需要知道需要调整的是哪一份请求。
初步代码
def process_orders(n, m, room_availability, orders):# 创建一个变量的副本。available_rooms = room_availability.copy()for order in orders:# 这里的话就是根据我当前拿到的订单,然后去。房间里面对应的去查看。d, start_day, end_day = orderfor day in range(start_day, end_day + 1):# 这里的话就是我当前的订单是。是不是可以剩余啊?如果说这里是。我当前的房间数量不能满足你的订单数啊那我就return一个负一。 # 那么我这里根据要求第一个行返回一个负一啊。第二行我返回当前的一个索引啊,也就是,呃,我当前是因为拿到了一行嘛,我当前拿到的是一行我当前拿到的一行的话,orders去调用这个index的方法。那就是看我当前的这个东西在你这里面的索引是多少啊?又因为Python是从零开始的,所以得加一。if available_rooms[day] < d:return -1, orders.index(order) + 1# 那么如果说我当前的房间是满足你的这个订单的话,那么我就减等于一啊,然后不断地过去。available_rooms[day] -= dreturn 0 if __name__ == "__main__":# n表示总共N个天数,总共有三个订单。n, m = map(int, input().split())# 这里输入每天房间可以用的情况。room_availability = list(map(int, input().split()))orders = []for _ in range(m):orders.append(list(map(int, input().split())))# 然后这边返回以后的话我们再对结果进行判断啊。这里是按照他的要求,如果是零的话返回给零,如果有不满足订单返回一个复议以及索引。 result, order_to_modify = process_orders(n, m, room_availability, orders)if result == 0:print(0)else:print(-1)print(order_to_modify)很显然,这样的思路有很大的优化的空间。这里我们只是单纯地对每一步进行操作。那么换1种思路。比如使用差分数组的方法,可以优化代码
// 这个函数实际上处理的是传入的这个NUM5之前的。进行检查。
bool check(int num){// 这里设置为零,就是单纯做一个初始化,然后下面用差分数组的方法啊,给它每一个区域的订单数都会拉伸或者啊做拉伸起来。for (int i=1;i<=num;i++){sub[s[i]] +=d[i];sub[t[i]+1]-=d[i];}// 然后这样的话,我们就得到了一个。一维的数组,里面存储着。订单的。每一天的订单的数量。for (int i=1;i<=n;i++){// 然后这里注意,因为这里是对区间进行处理,然后每一个订单里面它都是几天到几天啊,它需要增加多少订单数啊,所以它很明显就是天然就是一个差分数组的形式啊。假如说没有订单的话,那每天都是需求数都是零。啊,但是这里的话给了每天的订单,那么这里就直接使用差分数组的方式来进行处理。这里的// 这里的查封的意思实际上可以理解为前一天河道后一天的需求X啊,如果说订单是零的话,那么需求差就是全部是零啊,也就是上面这里写的这个啊,刚开始初始化的时候都设置为零,然后开始往里面加订单啊,哪一天到哪一天里面啊,需要增加多少的数量啊,所以很明显就天然。是一个查封数组的形式,然后上面由于我们这里是,呃,天然是一个茶壶数组的形式,那么我们使用查封数组拉伸区间的方法去对它进行相加。然后这里的话我们就需要得到他的原始的数据啊。如果说。我的需求数啊,是大于。我目前拥有的这个房间的数量那么很满,很显然就是满足条件了啊我就把return true。// 这里还有一点注意的就是它实际上是从一开始的。所以啊,这里就考虑到初始化的问题啊,我就不用初始化了然后每次第一列都是默认是零,然后我从一开始。need[i] = need[i-1] + sub[i];if (need[i]>r[i])return true;}return false;
}//主函数二分搜索// 那么如果说有一些订单是无法满足的。那么我为了提高效率啊,我就可以啊。每次只进行1/2的查找啊,就是找到这个最关键的时间点。呃,换句话说,这里实际上是找到那个问题,订单啊,最快的方法,那么我们可以很简单地用一个二分查找方。while (le<=ri){mid = le + (ri-le)/2;// 这里就是如果我发现了在左半部分是这个问题点,那么我就去左半部分找,否则的话我就去用半部分找。// ans的作用是记录当前,找到最大的订单数。// 这里特别要注意啊,就是二分查找它的前提必须是输入的数据是有序的,才能用二分查找这里因为提供给的他的数据都是有序的,所以我们可以直接用。if(check(mid)){ri = mid-1;// 并且由于是有序的,那么我在左半部分,它的最大值就是 中间最中间的那个。// 这里注意啊,为什么左半边有需要去Kan S复制啊?右半部分没有啊,首先这里的mid就是索引,我们看到上面Le和ri,呃,是一和M,这里是长度。那么这里给他整除了以后就是它中间的那个数啊,也就是表示的是索引,然后因为我们是从前往后逐个的去找。啊,这么那么在进行二分查找的过程中我们想过啊,如果是我们在左半部分找到了啊。那我们就压缩这个空间啊啊按从右往左,然后逐个的去压缩空间啊。如果说你在右边找到呢,那其实也一样啊,右边找到了以后,你到最后肯定是,呃,把这个空间给逐步缩小的。// 这里的文化an S放在这里,主要是从逻辑上来讲啊,因为我们的check函数是啊,以当前位置为准,然后向前去找这个问题点啊,如果说。呃,这个check函数它是为true的话,那么表示问题点在当前的维乾,那么就是以made made以前啊,那么made也是1种可能,并且是1种最大的可能性啊。所以说这里主要是因为逻辑原因啊,并不是别的什么原因。ans = mid; }else{le = mid+1; } 上面的代码为截取最关键的一部分分析,代码思路来源于bilbli轩哥码题,注释为随笔,只说明大概思路,
这里的订单处理问题很显然天然的用到了差分的思想。
N = 10**6def check(num, n, r, d, s, t):sub = [0] * (N + 1)for i in range(1, num + 1):sub[s[i]] += d[i]sub[t[i] + 1] -= d[i]need = [0] * (N + 1)for i in range(1, n + 1):need[i] = need[i - 1] + sub[i]if need[i] > r[i]:return Truereturn Falsedef main():n, m = map(int, input().split())r = [0] * (N + 1)d = [0] * (N + 1)s = [0] * (N + 1)t = [0] * (N + 1)temp_r = list(map(int, input().split()))for i in range(1, n + 1):r[i] = temp_r[i - 1]for i in range(m): temp = list(map(int, input().split()))d[i], s[i], t[i] = temple, ri = 1, mif not check(m, n, r, d, s, t):print(0)returnwhile le <= ri:mid = le + (ri - le) // 2if check(mid, n, r, d, s, t):ri = mid - 1ans = midelse:le = mid + 1print("-1")print(ans)if __name__ == "__main__":main()END
相关文章:
)
【算法实战】每日一题:17.1 订单处理问题(差分思想,二分搜索)
题目 一个会议中心的场地预订系统。在接下来的 n 天里,会议中心有一定数量的会议室可供租用。共有 m 份预订请求,每份请求描述为 (d_i, a_i, b_i),表示需要从第 a_i 天到第 b_i 天使用会议室(包括第 a_i 天和第 b_i 天࿰…...
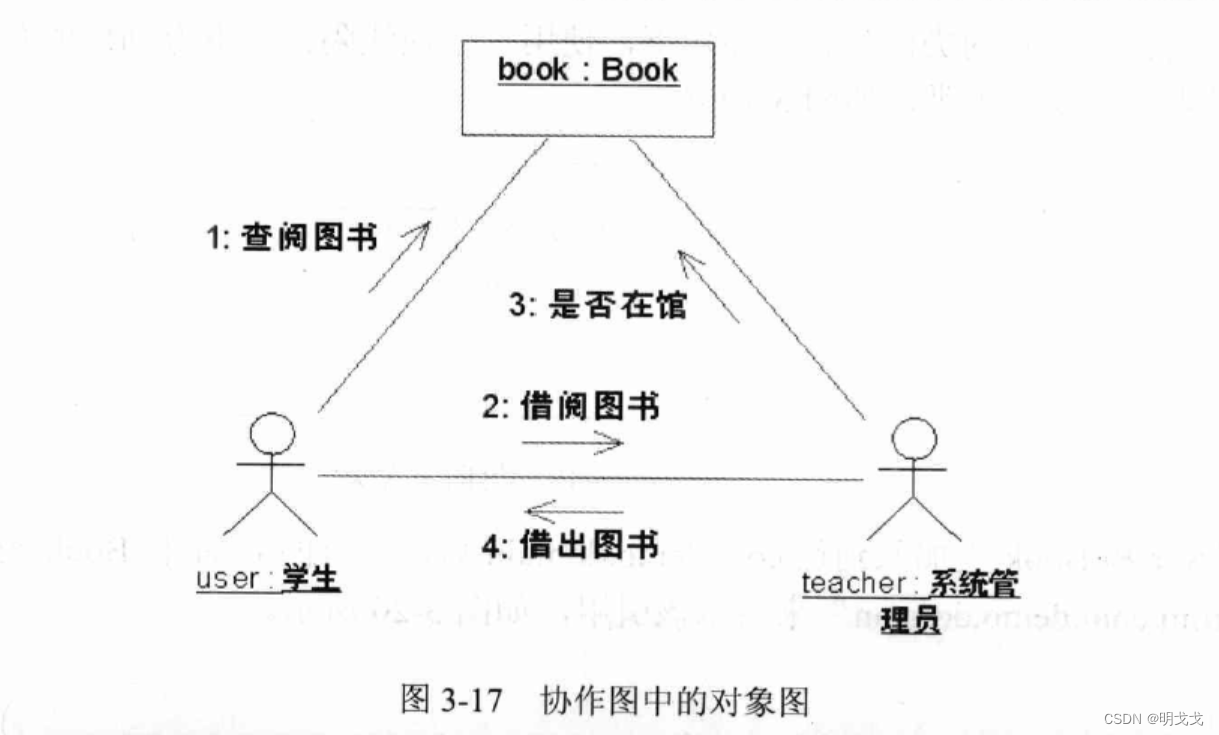
UML静态图-对象图
概述 静态图包含类图、对象图和包图的主要目的是在系统详细设计阶段,帮助系统设计人员以一种可视化的方式来理解系统的内部结构和代码结构,包括类的细节、类的属性和操作、类的依赖关系和调用关系、类的包和包的依赖关系。 对象图与类图之间的关系&…...

数据结构第三篇【链表的相关知识点一及在线OJ习题】
数据结构第三篇【链表的相关知识点一及在线OJ习题】 链表链表的实现链表OJ习题顺序表和链表的区别和联系 本文章主要讲解关于链表的相关知识,喜欢的可以三连喔 😀😃😄😄😊😊🙃&#…...

RabbitMQ-发布/订阅模式
RabbitMQ-默认读、写方式介绍 RabbitMQ-直连交换机(direct)使用方法 目录 1、发布/订阅模式介绍 2、交换机(exchange) 3、fanout交换机的使用方式 3.1 声明交换机 3.2 发送消息到交换机 3.2 扇形交换机发送消息代码 3.2 声明队列,用于接收消息 3.3 binding …...

客运提质增效新模式!苏州金龙客货邮融合公交闪耀2024道路运输展
5月31日,“2024北京国际商用车及零部件展览会”暨“2024北京国际道路客货运输车辆及零部件展览会”(简称为“2024道路运输车辆展”)在中国国际展览中心(顺义馆)落下帷幕。本届展会以“智能、绿色、安全,助力…...

【Python实战】使用postman测试flask api接口
cookie_demo.py # -*- coding: utf-8 -*- """ Time : 2024/5/28 17:14 Author : 娜年花开 File : cookie_demo.py Desc : 需求:用户需要先登陆,登陆之后,通过Cookie来判断是不是能够访问登录后的接口userinfo &quo…...

Docker大学生看了都会系列(二、Mac通过Homebrew安装Docker)
系列文章目录 第一章 Docker介绍 第二章 Mac通过Homebrew安装Docker 文章目录 前言Mac通过Homebrew安装本机环境系统要求terminal命令安装查看安装信息配置阿里云镜像加速登陆阿里云配置加速地址其他国内加速地址 总结 前言 在上一章了解了Docker容器是什么之后,本…...
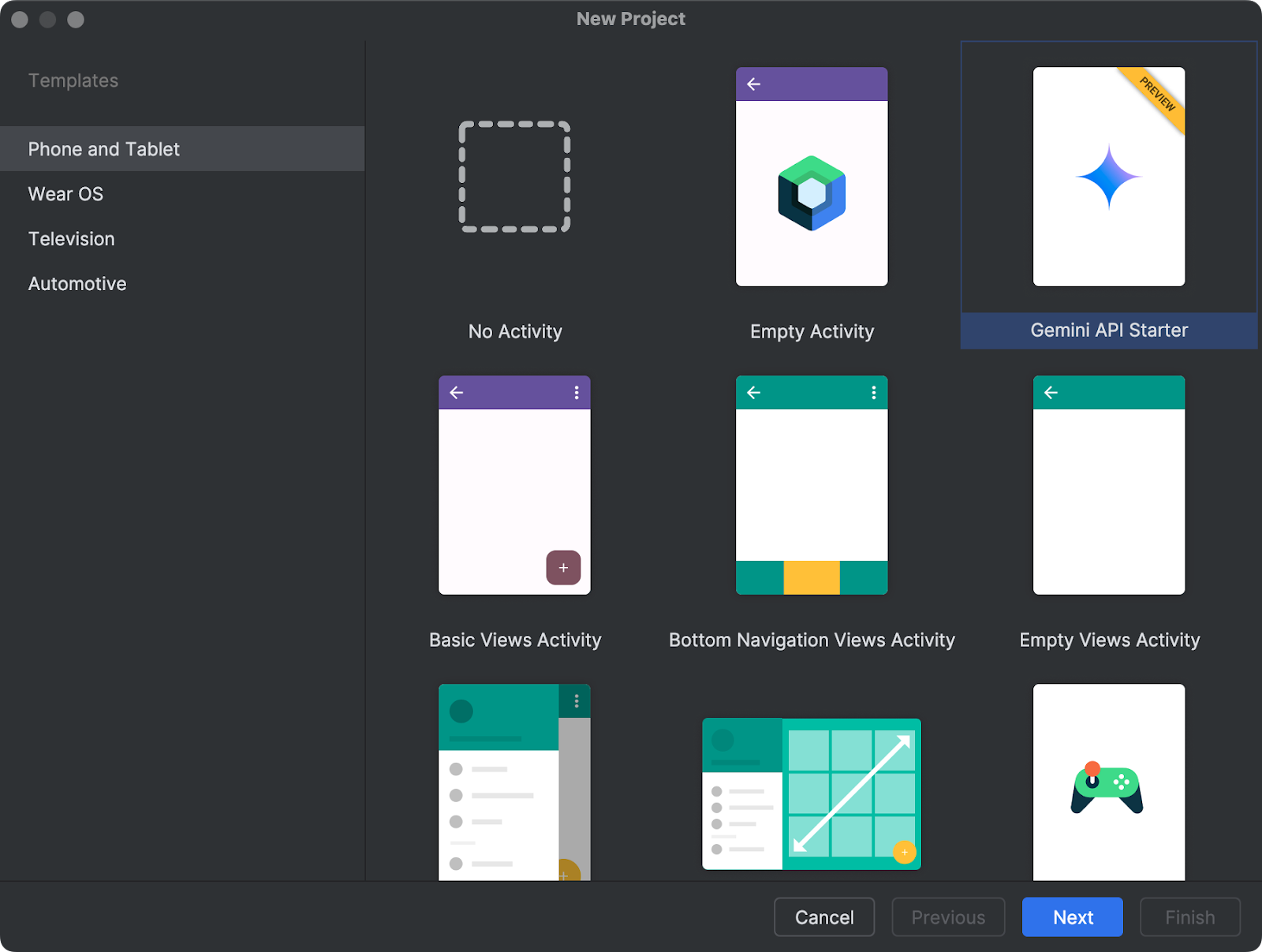
探索 Android Studio 中的 Gemini:加速 Android 开发的新助力
探索 Android Studio 中的 Gemini:加速 Android 开发的新助力 在 Gemini 时代的下一篇章中,Gemini融入了更多产品中,Android Studio 正在使用 Gemini 1.0 Pro 模型,使 Android 开发变得更快、更简单。 Studio Bot 现已更名为 And…...

linux运维——查看网卡实时流量脚本
方法一 以使用iftop命令来查看Linux系统中网卡的实时流量。如果您的系统还没有安装iftop,可以通过包管理器进行安装。 对于基于centos,可以使用以下命令安装: sudo yum install iftop 安装完成后,运行iftop命令查看实时流量&a…...

【三维重建NeRF(三)】Mip-NeRF论文解读
本文结合深蓝学院课程学习和本人的理解,欢迎交流指正 文章目录 Mip-NeRF流程简述混叠问题与MipMapMip-NeRF提出的解决办法圆锥台近似计算与集成位置编码(IPE) Mip-NeRF流程简述 Mip-NeRF的大体流程和NeRF基本是一样的,NeRF介绍 创新的部分就是针对NeRF…...
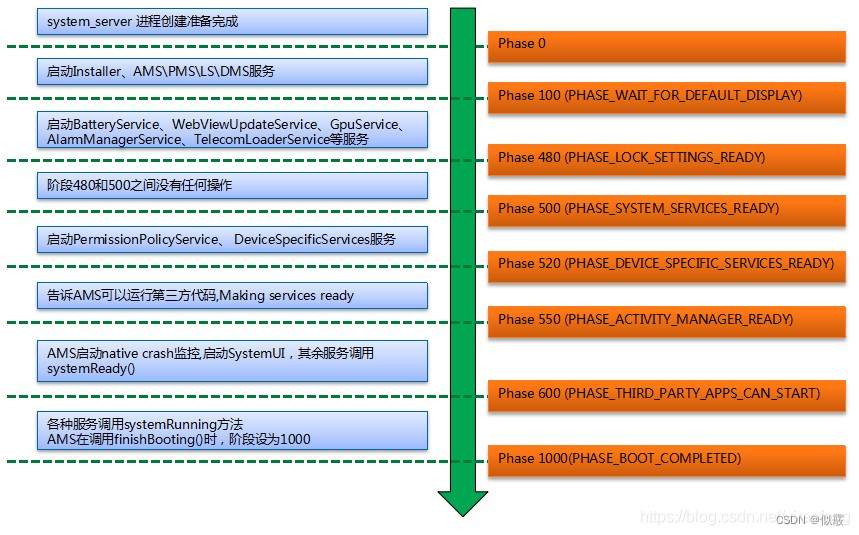
安卓SystemServer进程详解
目录 一、概述二、源码分析2.1 SystemServer fork流程分析2.1.1 [ZygoteInit.java] main()2.1.2 [ZygoteInit.java] forkSystemServer()2.1.3 [Zygote.java] forkSystemServer()2.1.4 [com_android_internal_os_Zygote.cpp]2.1.5 [com_android_internal_os_Zygote.cpp] ForkCom…...

Android studio 连接 adb传输文件到电脑
前提是已经连接到adb window R: 打开控制台adb devices:可以查看已经连接的设备adb pull /storage/emulated/0/Download/aa.png C:\Users\Administrator\Desktop:拉取连接设备的文件 aa.png 到电脑桌面上 (在电脑控制台进行拉取操作) 如果…...
)
Web学习篇(二)
命令执行漏洞 一、常用的函数 1、eval() 例: eval(string $code) 把字符串code作为PHP代码执行 2、assert() assert( mixed $assertion [, string $description ]) 检查一个断言是否为 FALSE,如果 assertion 是字符串,它将会被 assert()当做 PHP 代码来执行。 3、p…...

在Linux/Ubuntu/Debian系统中使用 `tar` 压缩文件
在Linux/Ubuntu/Debian系统中使用 tar 压缩文件 tar 命令是用于在类 Unix 操作系统中创建文件和目录存档的强大实用程序。 基本存档创建 要创建文件夹的简单存档,请使用以下命令: tar -cf ./my-archive.tar ./my-folder/此命令将创建一个名为 my-arc…...

Idea-Linux远程开发部署
第一步:File->Remote Development 第二步: 第三步: 第四步:在Host位置填写Linux虚拟机的IP地址,在Username、Password填写对应的账号密码后点击Test Connection测试连接。 第五步: 第六步:在…...

智能硬件会是下一个风口行业吗?
“风口行业”一直是人们热捧的择业目标,曾经红极一时房地产行业,此时已成沉舟侧畔之势,也意味着一个又一个行业时代的更迭。 随着5G时代的到来,“智能化”成了人们热议的话题,因为大家都懂:顺势而为才是王…...

mysql like 查询优化
1.如果我们查询的时候用like 模糊查询%a%,数据量大了会查询全局,效率很低 SELECT * FROM Customers WHERE CustomerName LIKE %a%; 优化: 不会破坏索引 -步骤-:创建适合Like查询的索引ALTER TABLE users ADD INDEX idx_username (usernam…...

3389连接器,3389连接器如何进行安全设置
在计算机网络领域,3389端口作为Windows系统默认的远程桌面协议(RDP)端口,在远程办公、技术支持等场景中发挥着重要作用。然而,由于其广泛的使用和直接暴露在互联网上的特性,3389端口也极易成为黑客攻击的目…...

代码随想录训练营Day56:Leetcode647、516
Leetcode647: 问题描述: 给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。 回文字符串 是正着读和倒过来读一样的字符串。 子字符串 是字符串中的由连续字符组成的一个序列。 示例 1: 输入:s &q…...

LLM主要类别架构
LLM主要类别架构介绍 LLM主要类别 LLM本身基于transformer架构。自2017年,attention is all you need诞生起,transformer模型为不同领域的模型提供了灵感和启发。基于原始的Transformer框架,衍生出了一系列模型,一些模型仅仅使用e…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...
