【动手学深度学习】softmax回归从零开始实现的研究详情



目录
🌊1. 研究目的
🌊2. 研究准备
🌊3. 研究内容
🌍3.1 softmax回归的从零开始实现
🌍3.2 基础练习
🌊4. 研究体会
🌊1. 研究目的
- 理解softmax回归的原理和基本实现方式;
- 学习如何从零开始实现softmax回归,并了解其关键步骤;
- 通过简洁实现softmax回归,掌握使用现有深度学习框架的能力;
- 探索softmax回归在分类问题中的应用,并评估其性能。
🌊2. 研究准备
- 根据GPU安装pytorch版本实现GPU运行研究代码;
- 配置环境用来运行 Python、Jupyter Notebook和相关库等相关库。
🌊3. 研究内容
启动jupyter notebook,使用新增的pytorch环境新建ipynb文件,为了检查环境配置是否合理,输入import torch以及torch.cuda.is_available() ,若返回TRUE则说明研究环境配置正确,若返回False但可以正确导入torch则说明pytorch配置成功,但研究运行是在CPU进行的,结果如下:
🌍3.1 softmax回归的从零开始实现
(1)使用jupyter notebook新增的pytorch环境新建ipynb文件,完成基本数据操作的研究代码与练习结果如下:
导入必要库和加载数据:
import torch
from IPython import display
from d2l import torch as d2lbatch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
初始化模型参数
num_inputs = 784
num_outputs = 10W = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True)
b = torch.zeros(num_outputs, requires_grad=True)实现softmax运算
X = torch.tensor([[1.0, 2.0, 3.0], [4.0, 5.0, 6.0]])
X.sum(0, keepdim=True), X.sum(1, keepdim=True)
def softmax(X):X_exp = torch.exp(X)partition = X_exp.sum(1, keepdim=True)return X_exp / partition # 这里应用了广播机制X = torch.normal(0, 1, (2, 5))
X_prob = softmax(X)
X_prob, X_prob.sum(1)
定义模型
def net(X):return softmax(torch.matmul(X.reshape((-1, W.shape[0])), W) + b)定义损失函数
y = torch.tensor([0, 2])
y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])
y_hat[[0, 1], y]![]()
def cross_entropy(y_hat, y):return - torch.log(y_hat[range(len(y_hat)), y])cross_entropy(y_hat, y)![]()
计算分类准确率
def accuracy(y_hat, y): #@save"""计算预测正确的数量"""if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:y_hat = y_hat.argmax(axis=1)cmp = y_hat.type(y.dtype) == yreturn float(cmp.type(y.dtype).sum())accuracy(y_hat, y) / len(y)![]()
def evaluate_accuracy(net, data_iter): #@save"""计算在指定数据集上模型的精度"""if isinstance(net, torch.nn.Module):net.eval() # 将模型设置为评估模式metric = Accumulator(2) # 正确预测数、预测总数with torch.no_grad():for X, y in data_iter:metric.add(accuracy(net(X), y), y.numel())return metric[0] / metric[1]class Accumulator: #@save"""在n个变量上累加"""def __init__(self, n):self.data = [0.0] * ndef add(self, *args):self.data = [a + float(b) for a, b in zip(self.data, args)]def reset(self):self.data = [0.0] * len(self.data)def __getitem__(self, idx):return self.data[idx]evaluate_accuracy(net, test_iter)![]()
训练模型
def train_epoch_ch3(net, train_iter, loss, updater): #@save"""训练模型一个迭代周期(定义见第3章)"""# 将模型设置为训练模式if isinstance(net, torch.nn.Module):net.train()# 训练损失总和、训练准确度总和、样本数metric = Accumulator(3)for X, y in train_iter:# 计算梯度并更新参数y_hat = net(X)l = loss(y_hat, y)if isinstance(updater, torch.optim.Optimizer):# 使用PyTorch内置的优化器和损失函数updater.zero_grad()l.mean().backward()updater.step()else:# 使用定制的优化器和损失函数l.sum().backward()updater(X.shape[0])metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())# 返回训练损失和训练精度return metric[0] / metric[2], metric[1] / metric[2]class Animator: #@save"""在动画中绘制数据"""def __init__(self, xlabel=None, ylabel=None, legend=None, xlim=None,ylim=None, xscale='linear', yscale='linear',fmts=('-', 'm--', 'g-.', 'r:'), nrows=1, ncols=1,figsize=(3.5, 2.5)):# 增量地绘制多条线if legend is None:legend = []d2l.use_svg_display()self.fig, self.axes = d2l.plt.subplots(nrows, ncols, figsize=figsize)if nrows * ncols == 1:self.axes = [self.axes, ]# 使用lambda函数捕获参数self.config_axes = lambda: d2l.set_axes(self.axes[0], xlabel, ylabel, xlim, ylim, xscale, yscale, legend)self.X, self.Y, self.fmts = None, None, fmtsdef add(self, x, y):# 向图表中添加多个数据点if not hasattr(y, "__len__"):y = [y]n = len(y)if not hasattr(x, "__len__"):x = [x] * nif not self.X:self.X = [[] for _ in range(n)]if not self.Y:self.Y = [[] for _ in range(n)]for i, (a, b) in enumerate(zip(x, y)):if a is not None and b is not None:self.X[i].append(a)self.Y[i].append(b)self.axes[0].cla()for x, y, fmt in zip(self.X, self.Y, self.fmts):self.axes[0].plot(x, y, fmt)self.config_axes()display.display(self.fig)display.clear_output(wait=True)def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater): #@save"""训练模型(定义见第3章)"""animator = Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0.3, 0.9],legend=['train loss', 'train acc', 'test acc'])for epoch in range(num_epochs):train_metrics = train_epoch_ch3(net, train_iter, loss, updater)test_acc = evaluate_accuracy(net, test_iter)animator.add(epoch + 1, train_metrics + (test_acc,))train_loss, train_acc = train_metricsassert train_loss < 0.5, train_lossassert train_acc <= 1 and train_acc > 0.7, train_accassert test_acc <= 1 and test_acc > 0.7, test_acclr = 0.1def updater(batch_size):return d2l.sgd([W, b], lr, batch_size)num_epochs = 10
train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, updater)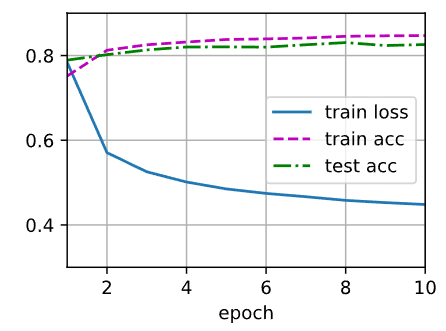
预测
def predict_ch3(net, test_iter, n=6):"""预测标签(定义见第3章)"""for X, y in test_iter:breaktrues = d2l.get_fashion_mnist_labels(y)preds = d2l.get_fashion_mnist_labels(net(X).argmax(axis=1))titles = [true +'\n' + pred for true, pred in zip(trues, preds)]d2l.show_images(X[0:n].reshape((n, 28, 28)), 1, n, titles=titles[0:n])predict_ch3(net, test_iter)
🌍3.2 基础练习
1.本节直接实现了基于数学定义softmax运算的softmax函数。这可能会导致什么问题?提示:尝试计算(\exp(50))的大小。
当计算exp(50)时,可能会遇到数值溢出的问题。softmax函数的定义是通过对输入向量中的每个元素进行指数运算,然后进行归一化,使得所有元素的和为1。指数函数在输入较大时会迅速增长,当输入超过一定阈值时,指数函数的输出将变得非常大,可能超出计算机所能表示的范围。
在本节直接实现的softmax函数中,如果输入向量中的某个元素较大(例如50),那么对应的指数运算结果将变得非常大,导致数值溢出。这会导致计算结果不准确或无法表示。在实际应用中,通常会使用数值稳定的方法来计算softmax函数,以避免数值溢出的问题。常见的数值稳定方法是通过减去输入向量中的最大值来进行计算,即softmax函数的输入进行平移。
因此,在直接实现基于数学定义的softmax函数时,可能会遇到数值溢出的问题,导致计算结果不准确或无法表示。
import numpy as npdef softmax(x):# 减去输入向量中的最大值,以避免数值溢出x -= np.max(x)# 计算指数运算exp_x = np.exp(x)# 归一化,计算softmax值softmax_x = exp_x / np.sum(exp_x)return softmax_x# 计算 exp(50) 的 softmax 值
x = np.array([50])
softmax_value = softmax(x)#这段代码通过减去输入向量中的最大值(在这种情况下就是50)来避免数值溢出。
#然后,使用NumPy的exp函数计算指数运算,最后进行归一化得到softmax值。
#由于采取了数值稳定的计算方法,即使输入为较大的数值(例如50),也能够正确计算softmax值。
#在这种情况下,softmax值为1,表示该元素在归一化后的向量中占比为100%。
print(softmax_value)结果:
![]()
2.本节中的函数cross_entropy是根据交叉熵损失函数的定义实现的。它可能有什么问题?提示:考虑对数的定义域。
根据提示考虑对数的定义域。交叉熵损失函数在计算中通常会涉及对数运算,而对数函数在定义域上有限制。对数函数的定义域是正实数,即输入值必须大于零。
在李沐老师的本节中,如果交叉熵损失函数的计算结果中包含负数或零,将会导致问题。这是因为对数函数在定义域之外没有定义,尝试对负数或零进行对数运算将会导致错误或异常。
特别是在计算softmax函数的交叉熵损失时,可能会遇到这样的问题。当预测值与真实值之间存在较大的差异时,交叉熵损失函数的计算结果可能会出现负数或零。这将导致对数运算无法进行,进而影响整个损失函数的计算。
为了解决这个问题,通常会在交叉熵损失函数的计算中添加一个小的平滑项,例如加上一个较小的常数(如10的-8次方)以确保避免出现负数或零。这被称为“平滑交叉熵”或“平滑对数损失”。
因此,如果在直接实现基于交叉熵损失函数的代码中,没有处理对数函数定义域的限制,可能会导致错误或异常,特别是在涉及预测值与真实值之间差异较大的情况下。
3.请想一个解决方案来解决上述两个问题。
为了解决上述两个问题,即数值溢出和对数函数定义域的限制,可以采取以下解决方案:
数值溢出问题:在计算softmax函数时,通过减去输入向量中的最大值来避免数值溢出。这样做可以确保指数函数的输入在合理的范围内,避免结果过大而导致数值溢出。这个方法在前面的回答中已经提到了。
对数函数定义域问题:在计算交叉熵损失函数时,添加一个小的平滑项。可以在对数函数的输入上加上一个较小的常数,例如(如10的-8次方),以确保避免出现负数或零。这样可以避免对数函数在定义域之外的值上计算,确保损失函数的计算结果正确。
下面是一个示例代码,展示了如何结合这两个解决方案来计算softmax函数和交叉熵损失函数:
import numpy as npdef softmax(x):x -= np.max(x)exp_x = np.exp(x)softmax_x = exp_x / np.sum(exp_x)return softmax_xdef cross_entropy(predicted, target):# 添加平滑项,避免对数函数定义域的问题smooth = 1e-8# 计算交叉熵损失loss = -np.sum(target * np.log(predicted + smooth))return loss# 假设有一个预测向量和真实标签向量
predicted = np.array([0.9, 0.1, 0.2])
target = np.array([1, 0, 0])# 计算softmax函数的输出
softmax_output = softmax(predicted)# 计算交叉熵损失
loss = cross_entropy(softmax_output, target)print(loss)结果:
![]()
在这段代码中,我们在softmax函数中采用了减去最大值的方法,以避免数值溢出。在交叉熵损失函数中,添加了平滑项(如10的-8次方)以确保避免对数函数的定义域问题。通过结合这两个解决方案,可以在计算softmax函数和交叉熵损失函数时避免数值溢出和对数函数定义域的限制,从而得到准确的计算结果。
4.返回概率最大的分类标签总是最优解吗?例如,医疗诊断场景下可以这样做吗?
在一些情况下,返回概率最大的分类标签可以是一个合理的决策,但并不总是最优解。特别是在医疗诊断等重要领域,仅仅依靠概率最大的分类标签可能会带来一些问题。
以下是一些原因:
- 不确定性:分类模型的预测结果往往包含一定程度的不确定性。即使一个类别的概率最大,但它的概率可能仍然相对较低。仅仅基于最大概率进行决策可能会忽略其他类别的潜在可能性。
- 类别之间的差异:在某些情况下,不同类别之间的重要性或影响力可能会有所不同。概率最大的类别可能不是最重要的类别,或者可能不是需要优先考虑的类别。
- 风险和成本:在医疗诊断等领域,决策的结果可能会对患者的生命和健康产生直接影响。仅仅基于概率最大的分类标签进行决策可能会忽略可能的风险和成本,导致不准确的结果或不适当的行动。
因此,在医疗诊断场景下,通常需要更细致的分析和决策过程。除了分类模型的输出概率,还需要考虑其他因素,例如患者的病史、症状、实验室检查结果等。医疗决策往往是复杂的,并需要由专业医生进行综合判断。
尽管返回概率最大的分类标签在某些情况下可能是合理的,但在医疗诊断等重要领域,仅仅依靠概率最大的分类标签并不足够,需要综合考虑其他因素,并由专业人士进行决策。
5.假设我们使用softmax回归来预测下一个单词,可选取的单词数目过多可能会带来哪些问题?
- 当可选取的单词数目过多时,使用softmax回归来预测下一个单词可能会面临以下问题:
- 计算复杂度增加:Softmax回归的计算复杂度与类别数目成正比。如果可选取的单词数目非常大,那么计算softmax函数的指数运算和归一化操作将变得非常昂贵,导致训练和推理的效率下降。
- 内存消耗增加:计算softmax函数所需的内存空间与类别数目成正比。当可选取的单词数目非常多时,需要存储大量的权重参数和临时计算结果,这可能导致内存消耗过大,甚至超过可用的内存限制。
- 数据稀疏性问题:当可选取的单词数目非常多时,每个单词的出现频率可能会变得非常稀疏。这会导致模型在训练过程中难以准确地估计每个单词的权重参数,从而影响模型的性能和泛化能力。
- 样本不平衡问题:在大规模的单词集中,不同单词的出现频率可能会有很大差异,导致样本不平衡问题。某些常见的单词可能会有更多的训练样本,而一些罕见的单词可能只有很少的训练样本。这会影响模型对于不常见单词的预测能力。
为了解决上述问题,可以采取一些技术手段,例如:
- 降低可选取的单词数目:可以通过限制词汇表的大小或使用更精确的单词选择方法,减少可选取的单词数目,从而降低计算和内存的负担。
- 使用分层softmax或负采样等技术:这些技术可以减少计算复杂度和内存消耗,同时处理数据稀疏性和样本不平衡问题。
- 使用更高级的模型:除了softmax回归,还可以尝试其他模型,如深度神经网络、注意力机制等,以提高模型的表达能力和性能。
🌊4. 研究体会
通过这次研究,我深入学习了softmax回归模型,理解了它的原理和基本实现方式。开始了解softmax回归的背景和用途,它在多类别分类问题中的应用广泛;学习了如何从零开始实现softmax回归,并掌握了其中的关键步骤。
在从零开始实现softmax回归时,首先需要构建模型的参数,包括权重和偏差。通过使用Python和NumPy库,能够方便地进行矩阵运算,计算模型的预测结果。然后,实现了softmax函数,它将模型的原始输出转化为概率分布。通过对softmax函数的应用,可以得到每个类别的概率预测。接下来,定义了损失函数,使用交叉熵损失来度量模型预测与真实标签之间的差异。通过最小化损失函数,可以优化模型的参数,使得模型的预测更加准确。在优化过程中,采用了梯度下降算法,通过计算损失函数关于参数的梯度,更新参数的数值。
通过简洁实现softmax回归,更加熟悉了深度学习框架的使用。可以通过几行代码完成模型的定义、数据的加载和训练过程。还学会了使用框架提供的工具来评估模型的性能,如计算准确率和绘制混淆矩阵。这使能够更方便地对模型进行调试和优化,以获得更好的分类结果。
最后,通过实验探索了softmax回归在分类问题中的应用,并评估了其性能。使用了一些真实的数据集,如MNIST手写数字数据集,来进行实验。在实验中,将数据集划分为训练集和测试集,用训练集来训练模型,然后用测试集来评估模型的性能。
在从零开始实现的实验中,对模型的性能进行了一些调优,比如调整学习率和迭代次数。观察到随着迭代次数的增加,模型的训练损失逐渐下降,同时在测试集上的准确率也在提升。这证明了的模型在一定程度上学习到了数据的规律,并能够泛化到新的样本。


相关文章:

【动手学深度学习】softmax回归从零开始实现的研究详情
目录 🌊1. 研究目的 🌊2. 研究准备 🌊3. 研究内容 🌍3.1 softmax回归的从零开始实现 🌍3.2 基础练习 🌊4. 研究体会 🌊1. 研究目的 理解softmax回归的原理和基本实现方式;学习…...
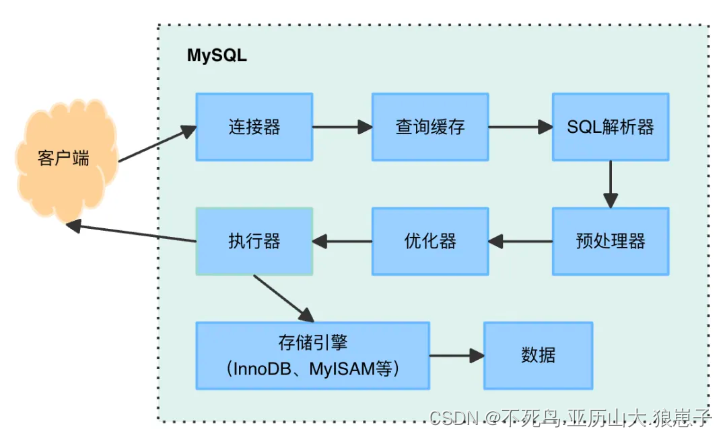
MySQL:MySQL执行一条SQL查询语句的执行过程
当多个客户端同时连接到MySQL,用SQL语句去增删改查数据,针对查询场景,MySQL要保证尽可能快地返回客户端结果。 了解了这些需求场景,我们可能会对MySQL进行如下设计: 其中,连接器管理客户端的连接,负责管理连接、认证鉴权等;查询缓存则是为了加速查询,命中则直接返回结…...

解决Python导入第三方模块报错“TypeError: the first argument must be callable”
注意以下内容只对导包时遇到同样的报错会有参考价值。 问题描述 当你尝试导入第三方模块时,可能会遇到如下报错信息: TypeError: the first argument must be callable 猜测原因 经过仔细检查代码,我猜测这个错误的原因是由于变量名冲突所…...

在python中连接了数据库后想要在python中通过图形化界面显示数据库的查询结果,请问怎么实现比较好? /ttk库的treeview的使用
在Python中,你可以使用图形用户界面(GUI)库来显示数据库的查询结果。常见的GUI库包括Tkinter(Python自带)、PyQt、wxPython等。以下是一个使用Tkinter库来显示数据库查询结果的简单示例。 首先,你需要确保…...
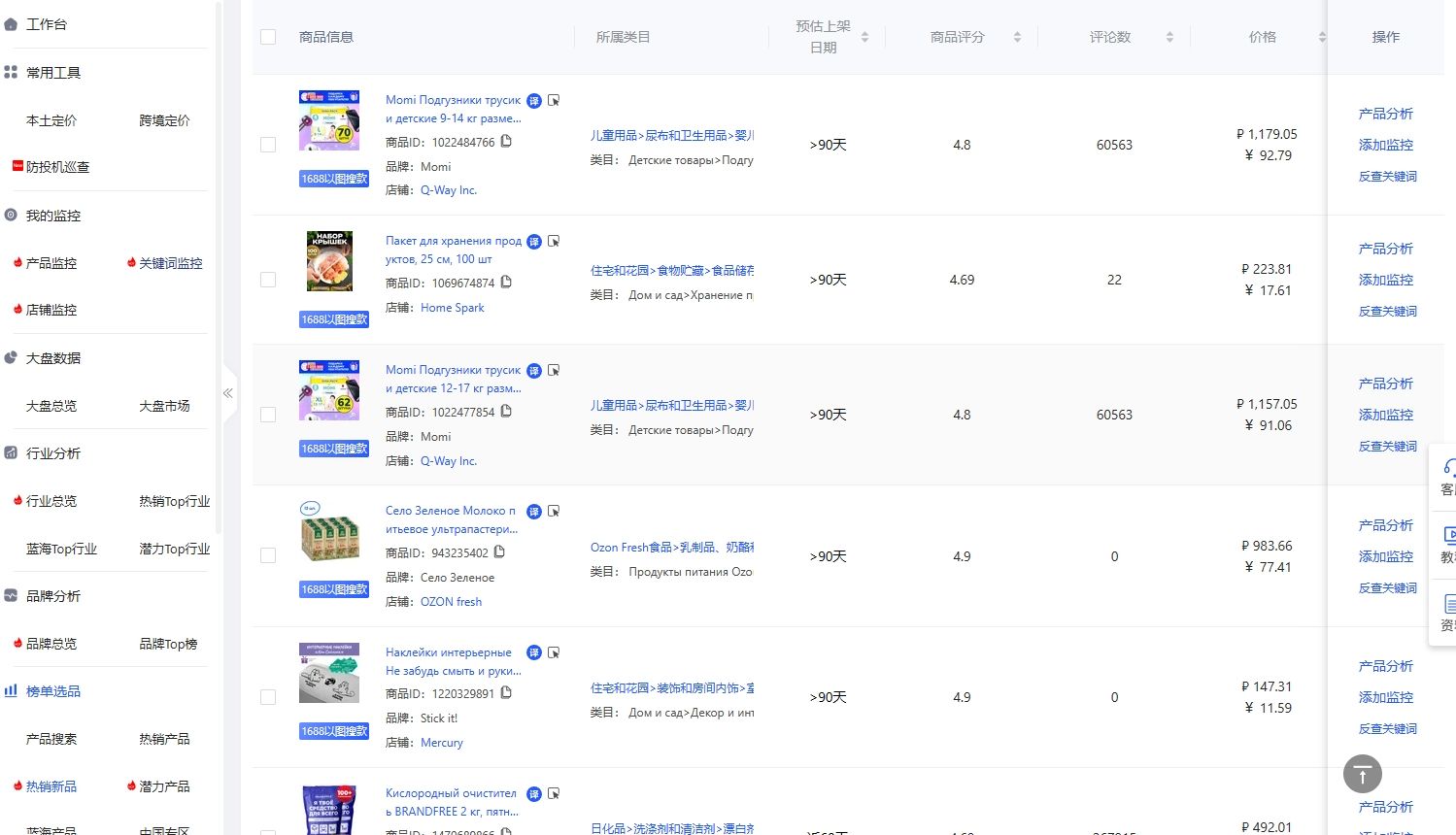
OZON的选品工具,OZON选品工具推荐
在电商领域,选品一直是决定卖家成功与否的关键因素之一。随着OZON平台的崛起,越来越多的卖家开始关注并寻求有效的选品工具,以帮助他们在这个竞争激烈的市场中脱颖而出。本文将详细介绍OZON的选品工具,并推荐几款实用的辅助工具&a…...
营销方案撰写秘籍:包含内容全解析,让你的方案脱颖而出
做了十几年品牌,策划出身,混迹过几个知名广告公司,个人经验供楼主参考。 只要掌握以下这些营销策划案的要点,你就能制作出既全面又专业的策划案,让你的工作成果不仅得到同事的认可,更能赢得老板的赏识&…...
如何制作一本温馨的电子相册呢?
随着科技的不断发展,电子相册已经成为了一种流行的方式来记录和分享我们的生活。一张张照片,一段段视频,都能让我们回忆起那些温馨的时光。那么,如何制作一本温馨的电子相册呢? 首先,选择一款合适的电子相册…...

485通讯网关
在工业自动化与智能化的浪潮中,数据的传输与交互显得尤为重要。作为这一领域的核心设备,485通讯网关凭借其卓越的性能和广泛的应用场景,成为了连接不同设备、不同协议之间数据转换和传输的桥梁。在众多485通讯网关中,HiWoo Box以其…...

Anaconda中的常用科学计算工具
Anaconda中的常用科学计算工具 Anaconda是一个流行的Python科学计算环境,它提供了大量的科学计算工具,这些工具可以帮助用户进行数据分析、机器学习、深度学习等任务。以下是一些常见的Anaconda中的科学计算工具: NumPy:一个用于…...
Java 中BigDecimal传到前端后精度丢失问题
1.用postman访问接口,返回的小数点精度正常 2.返回到页面里的,小数点丢失 3.解决办法,在字段上加注解 JsonFormat(shape JsonFormat.Shape.STRING) 或者 JsonSerialize(using ToStringSerializer.class) import com.fasterxml.jackson.a…...

在Linux/Ubuntu/Debian上安装TensorFlow 2.14.0
在Ubuntu上安装TensorFlow 2.14.0,可以遵循以下步骤。请注意,由于TensorFlow的版本更新可能很快,这里提供的具体步骤可能需要根据你的系统环境和实际情况进行微调。 准备工作 检查系统要求:确保你的Ubuntu系统满足TensorFlow的运…...

多语言for循环遍历总结
多语言for循环遍历总结 工作中经常需要遍历对象,但不同编程语言之间存在一些细微差别。为了便于比较和参考,这里对一些常用的遍历方法进行了总结。 JAVA 数组遍历 Test void ArrayForTest() {String[] array {"刘备","关羽", &…...
python API自动化(Jsonpath断言、接口关联及加密处理)
JsonPath应用及断言 重要 自动化要解决的核心问题 :进行自动测试-自动校验(进行结果的校验 主要能够通过这个方式提取数据业务场景:断言 、接口关联 {key:value}网址:附:在线解析 JSONPath解析器 - 一个工具箱 - 好用…...

C++入门5——C/C++动态内存管理(new与delete)
目录 1. 一图搞懂C/C的内存分布 2. 存在动态内存分配的原因 3. C语言中的动态内存管理方式 4. C内存管理方式 4.1 new/delete操作内置类型 4.2 new/delete操作自定义类型 1. 一图搞懂C/C的内存分布 说明: 1. 栈区(stack):在…...

leetcode 743.网络延时时间
思路:迪杰斯特拉最短路径 总结起来其实就两件事: 1.从所给起点开始能不能到达所有点; 2.如果能够到达所有点,那么这个时候需要判断每一个点到源点的最短距离,然后从这些点中求出最大值。 所以用最小路径求解是最划…...
MATLAB导入导出Excel的方法|读与写Excel的命令|附例程的github下载链接
前言 前段时间遇到一个需求:导出变量到Excel里面,这里给出一些命令,同时给一个示例供大家参考。 MATLAB读/写Excel的命令 在MATLAB中,可以使用以下命令来读写Excel文件: 读取Excel文件: xlsread(filen…...
)
【第4章】SpringBoot实战篇之登录优化(含redis使用)
文章目录 前言一、整合redis1. 引入库2. 配置 二、登录优化1.登录2.拦截器3. 登出4. 修改密码 总结 前言 上一章的登录接口,我们将用户登录信息放置于Map中,存在一个问题,集群部署无法共享以及应用停止用户登录信息即丢失,接下来我们整合redis来整合这个问题。 一、整合redis …...

数据结构:详解二叉树(树,二叉树顺序结构,堆的实现与应用,二叉树链式结构,链式二叉树的4种遍历方式)
目录 1.树的概念和结构 1.1树的概念 1.2树的相关概念 1.3树的代码表示 2.二叉树的概念及结构 2.1二叉树的概念 2.2特殊的二叉树 2.3二叉树的存储结构 2.3.1顺序存储 2.3.2链式存储 3.二叉树的顺序结构和实现 3.1二叉树的顺序结构 3.2堆的概念和结构 3.3堆的特点 3…...
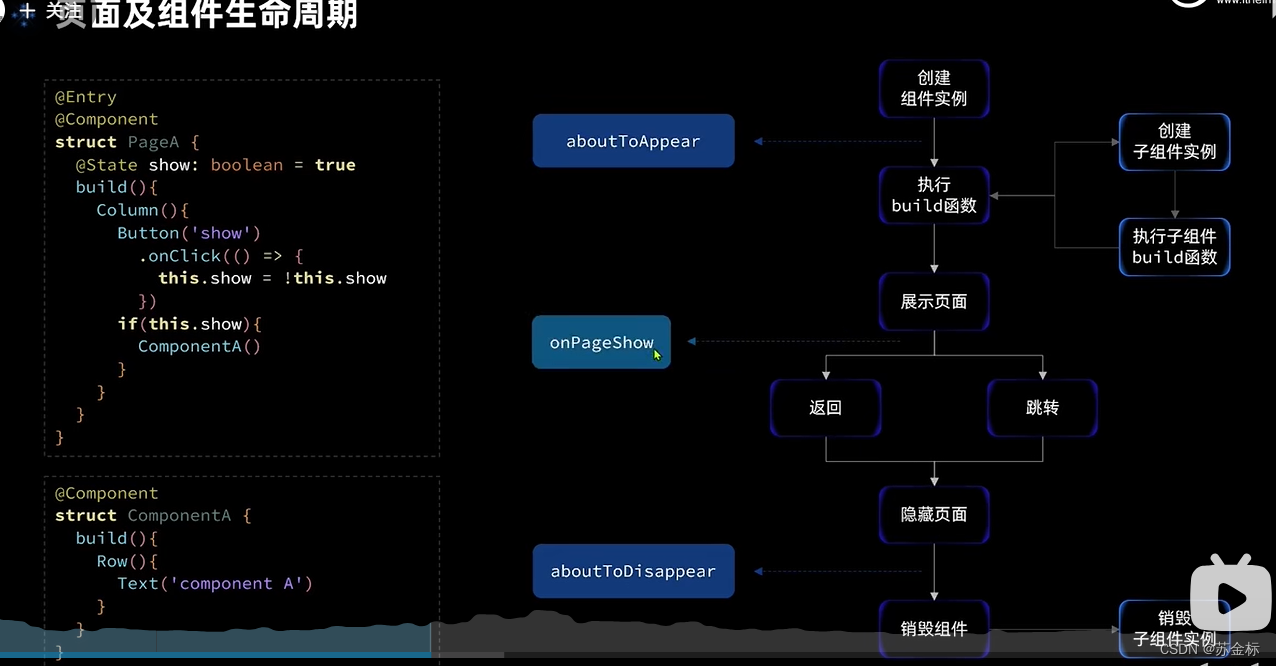
HarmonyOS-9(stage模式)
配置文件 {"module": {"requestPermissions": [ //权限{"name": "ohos.permission.EXECUTE_INSIGHT_INTENT"}],"name": "entry", //模块的名称"type": "entry", //模块类型 :ability类型和…...

RestTemplate代码内部访问RESTful服务的客户端工具
1. 前言 在当今的互联网时代,RESTful服务已经成为了一种流行的服务架构风格,它提供了简单、轻量级、灵活、可扩展的方式来构建和访问Web服务。而在Java开发中,Spring框架提供了一个非常方便的工具——RestTemplate,用于访问和调用…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...
