O2O : Finetuning Offline World Models in the Real World
CoRL 2023 Oral
paper
code
Intro
算法基于TD-MPC,利用离线数据训练世界模型,然后在线融合基于集成Q的不确定性估计实现Planning。得到的在线数据将联合离线数据共同训练目标策略。
Method

TD-MPC
TD-MPC由五部分构成:
- 状态特征提取 z = h θ ( s ) z = h_\theta(s) z=hθ(s)
- 隐动力学模型 z ′ ‘ = d θ ( z , a ) z'`=d_\theta(z,a) z′‘=dθ(z,a)
- 奖励模型 r ^ = R θ ( z , a ) \hat{r}=R_\theta(z,a) r^=Rθ(z,a)
- planning policy a ^ = π θ ( z ) \hat{a}=\pi_\theta(z) a^=πθ(z)
- 终止状态下的 q ^ = Q θ ( z , a ) \hat{q}=Q_\theta(z,a) q^=Qθ(z,a)
通过联合训练进行优化,损失函数为:
L ( θ ) = E ( s , a , r , s ′ ) 0 : h ∼ B ⌊ ∑ t = 0 h ( ∥ z t ′ − s g ( h ϕ ( s t ′ ) ) ∥ 2 2 ⏟ Latent dynamics + ∥ r ^ t − r t ∥ 2 2 ⏟ Reward + ∥ q ^ t − q t ∥ 2 2 ⏟ Value − Q θ ( z t , a ^ t ) ⏟ Action ) ⌋ ( 1 ) \mathcal{L}(\theta)=\mathbb{E}_{(\mathbf{s},\mathbf{a},r,\mathbf{s}^{\prime})_{0:h}\sim\mathcal{B}}\left\lfloor\sum_{t=0}^{h}\left(\underbrace{\|\mathbf{z}_{t}^{\prime}-\mathrm{sg}(h_{\phi}(\mathbf{s}_{t}^{\prime}))\|_{2}^{2}}_{\text{Latent dynamics}}+\underbrace{\|\hat{r}_{t}-r_{t}\|_{2}^{2}}_{\text{Reward}}+\underbrace{\|\hat{q}_{t}-q_{t}\|_{2}^{2}}_{\text{Value}}-\underbrace{Q_{\theta}(\mathbf{z}_{t},\hat{\mathbf{a}}_{t})}_{\text{Action}}\right)\right\rfloor(1) L(θ)=E(s,a,r,s′)0:h∼B t=0∑h Latent dynamics ∥zt′−sg(hϕ(st′))∥22+Reward ∥r^t−rt∥22+Value ∥q^t−qt∥22−Action Qθ(zt,a^t) (1)
在Offline 设定下,分布偏移将导致Q估计以及隐模型以及价值函数的错误估计。启发于IQL,通过只对in-sample的动作尽心TD-backups来估计,缓解过估计问题。因此对模型价值函数利用离线数据进行训练时,此时Q函数采用IQL中的期望回归方法优化
L V ( θ ) = ∣ τ − 1 { Q ϕ ( z t , a t ) − V θ ( z t ) < 0 } ∣ ( Q ϕ ( z t , a t ) − V θ ( z t ) ) 2 , \mathcal{L}_{V}(\theta)=|\tau-1_{\{Q_{\phi}(\mathbf{z}_{t},\mathbf{a}_{t})-V_{\theta}(\mathbf{z}_{t})<0\}}|(Q_{\phi}(\mathbf{z}_{t},\mathbf{a}_{t})-V_{\theta}(\mathbf{z}_{t}))^{2}, LV(θ)=∣τ−1{Qϕ(zt,at)−Vθ(zt)<0}∣(Qϕ(zt,at)−Vθ(zt))2,
同时对planning policy采用AWR的更新,即 exp ( β ( Q ϕ ( z t , a t ) − V θ ( z t ^ ) ) ) log π θ ( a t ∣ z t ) \exp(\beta(Q_\phi(\mathbf{z}_t,\mathbf{a}_t)-V_\theta(\hat{\mathbf{z}_t})))\log\pi_\theta(\mathbf{a}_t|\mathbf{z}_t) exp(β(Qϕ(zt,at)−Vθ(zt^)))logπθ(at∣zt)
Uncertainty Estimation as Test-Time Behavior Regularizatio
离线训练的模型依旧存在OOD数据过估计,需要在线微调。文章提出基于不确定性估计的planning实现在线交互过程中的动作选择。planning一定程度缓解基于约束的离线算法导致的在现阶段探索能力不足。进而导致算法样本效率低的问题。
首先构建集成Q函数模型,计算基于标准差的不确信度,作为惩罚项对奖励进行调整,实现保守的在线planning。
R ^ = γ h ( Q θ ( z h , a h ) − λ u h ) + ∑ t = 0 h − 1 γ t ( R θ ( z t , a t ) − λ u t ) , u t = s t d ( { Q θ ( i ) ( z t , a t ) } i = 1 N ) \hat{\mathcal{R}}=\gamma^{h}\left(Q_{\theta}(\mathbf{z}_{h},\mathbf{a}_{h})-\lambda u_{h}\right)+\sum_{t=0}^{h-1}\gamma^{t}\left(R_{\theta}(\mathbf{z}_{t},\mathbf{a}_{t})-\lambda u_{t}\right),\quad u_{t}=\mathrm{std}\left(\{Q_{\theta}^{(i)}(\mathbf{z}_{t},\mathbf{a}_{t})\}_{i=1}^{N}\right) R^=γh(Qθ(zh,ah)−λuh)+t=0∑h−1γt(Rθ(zt,at)−λut),ut=std({Qθ(i)(zt,at)}i=1N)
除此外,还维护两个buffer分别存储离线数据于在线数据,通过balance sampling数据训练模型、策略以及价值函数。
结果

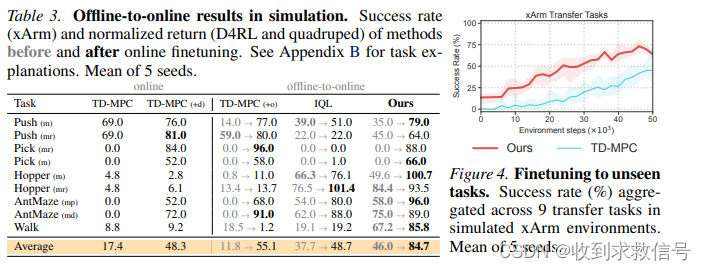
相关文章:

O2O : Finetuning Offline World Models in the Real World
CoRL 2023 Oral paper code Intro 算法基于TD-MPC,利用离线数据训练世界模型,然后在线融合基于集成Q的不确定性估计实现Planning。得到的在线数据将联合离线数据共同训练目标策略。 Method TD-MPC TD-MPC由五部分构成: 状态特征提取 z h θ ( s ) …...
)
嵌入式学习(Day:31 网络编程2:TCP)
client, server browser b/s http p2p peer TCP的特征:1.有链接;2.可靠传输;3.流式套接字 1、模式 C/S 模式 》服务器/客户端模型(服务端1个,客户端很多个) server:socket()-->bind()---…...

正则表达式 0.1v
正则表达式 扩展 --> :% s/\///g //文件里面所有的 / 去掉 * 通配符 \ //转义,让字符变成原本的意思 ^ //行首 $ //行尾 [0-9] //数字 [a-z] //小写字母 [A-Z] //大写字母 把文件的小写字母替换为大写字母? 固定写法 :% s/[a-…...
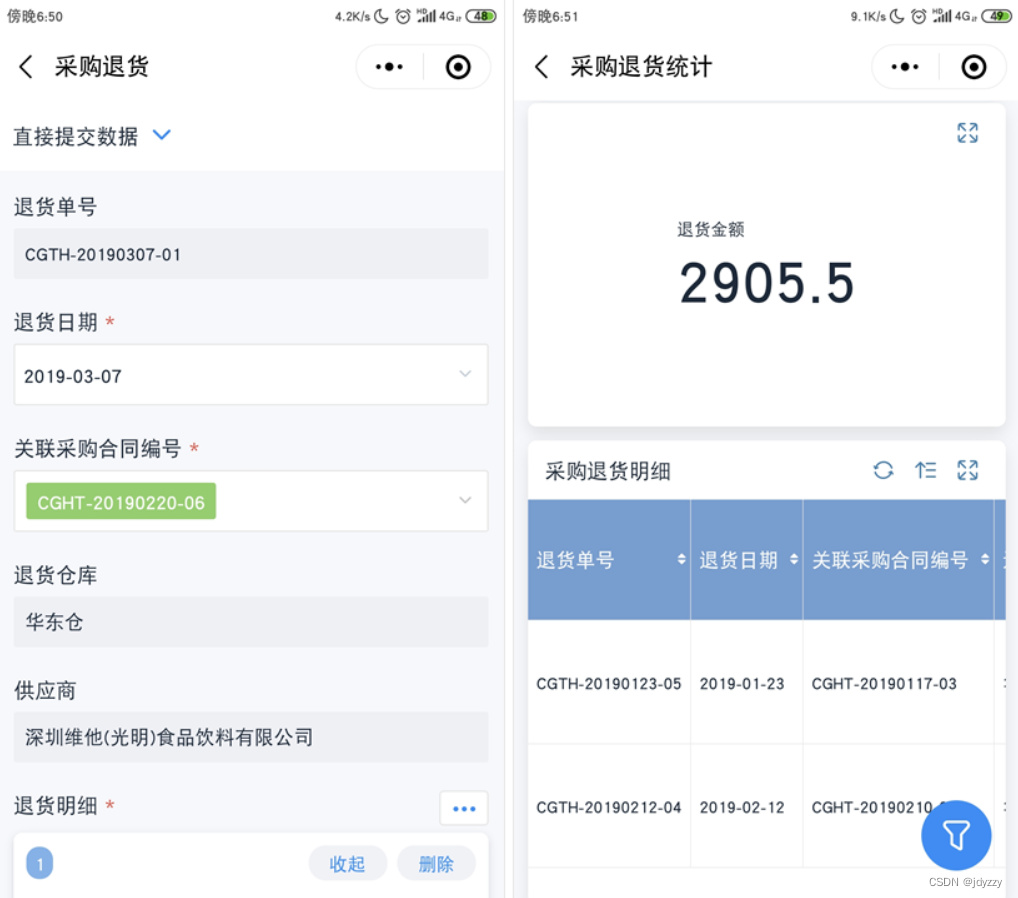
免费的仓库出入库管理软件有哪些?
中小企业因为预算有限,所以希望能在出入库管理软件方面能够减少成本。 但我们必须清醒地认识到,所谓的“永久免费”往往只是一个幌子。这些软件要么是新上市的、功能尚未完善的产品,试图通过免费吸引用户试用;要么在数据安全和客…...
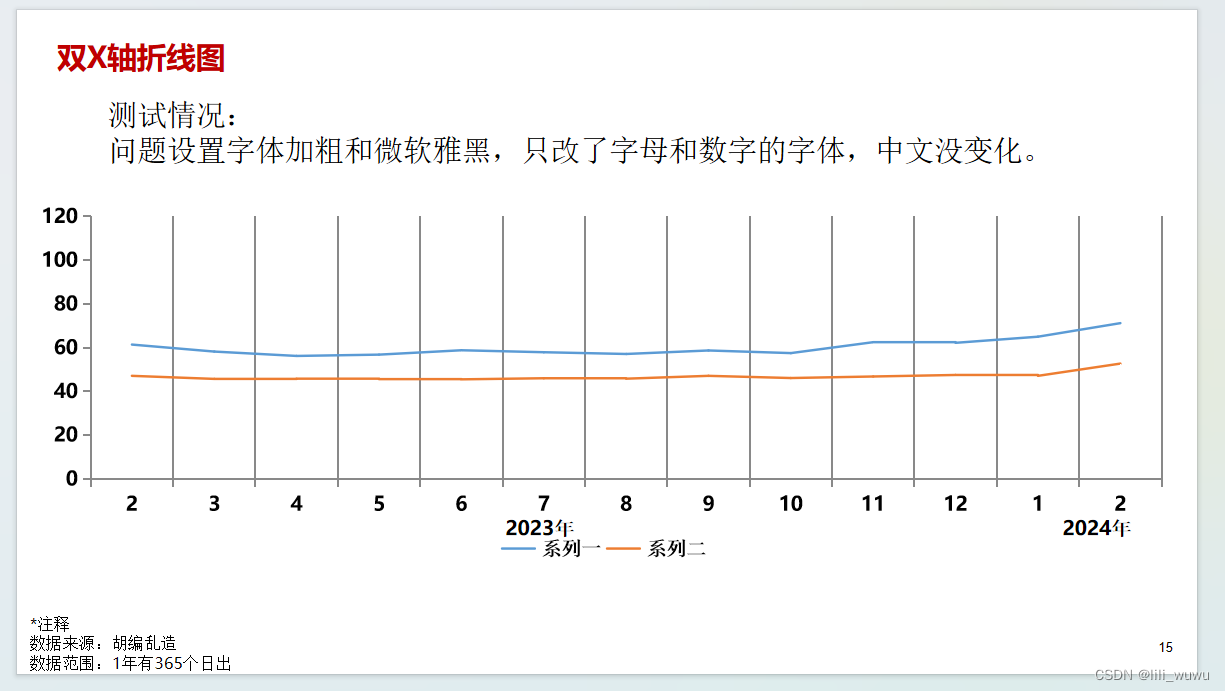
python 办公自动化-生成ppt文本和图
最终样式 代码实现 # 可编辑折线写入文字 成功 # 问题: 设置字体类型和加粗和字体为微软雅黑,是只改了字母和数字的字体,中文没变化 pip install pptx_ea_font 这个库可以解决这个问题 import pandas as pd import pptx_ea_font import mat…...

「动态规划」买卖股票的最佳时机
力扣原题链接,点击跳转。 给定一个整数数组prices,prices[i]表示股票在第i天的价格。你最多完成2笔交易。你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。设计一个算法计算最大利润。 我们用动态规划的思想来解决…...

Java 并发编程面试二
目录 一、并发编程三要素? 二、实现可见性的方法有哪些? 三、多线程的价值? 四、创建线程的有哪些方式? 五、创建线程的三种方式的对比? 六、Java 线程具有五中基本状态 七、什么是线程池?有哪几种创建方式 八、四种线程池的创建 九、线程池的优点? 十、常用的…...

成功解决“ModuleNotFoundError: No Module Named ‘utils’”错误的全面指南
成功解决“ModuleNotFoundError: No Module Named ‘utils’”错误的全面指南 在Python编程中,遇到ModuleNotFoundError: No Module Named utils这样的错误通常意味着Python解释器无法找到名为utils的模块。这可能是由于多种原因造成的,比如模块确实不存…...
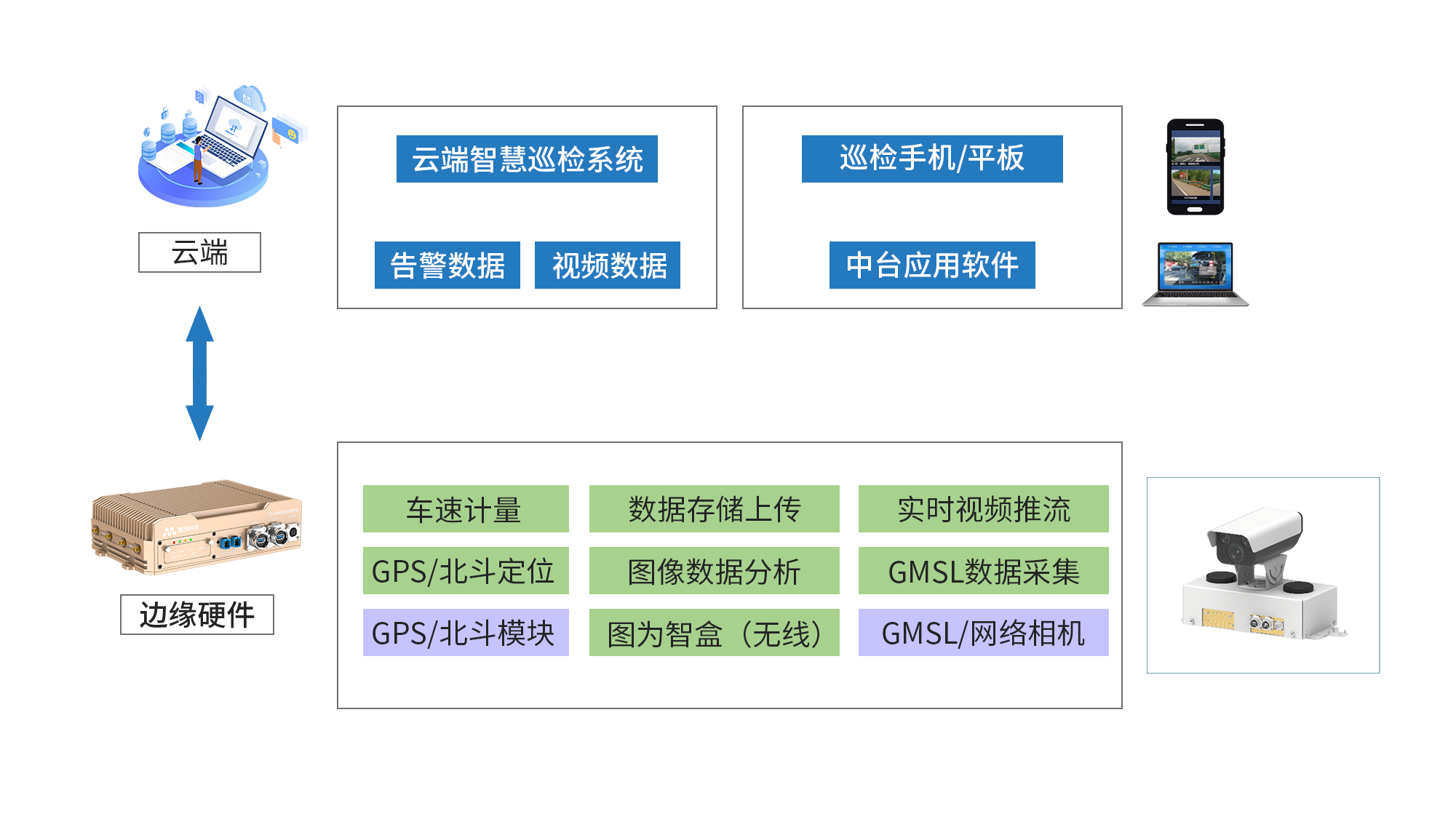
Nvidia Jetson/Orin +FPGA+AI大算力边缘计算盒子:公路智能巡检解决方案
项目背景 中国公路网络庞大,总里程超过535万公里,高速公路里程位居世界前列。面对基础设施存量的不断增长,公路养护管理已迈入“建管养并重”的新时代。随着养护支出的逐年攀升,如何提升养护效率、降低管理成本,成为亟…...

【Maxcompute】geohash转经纬度,经纬度转geohash,计算geohash九宫格
1.梳理、总结经纬度处理在Maxcompute平台上的实战应用,如geohash转经纬度,经纬度转geohash,计算geohash九宫格等。 2.欢迎批评指正,跪谢一键三连! 文章目录 1.部署代码1.部署代码 部署至Maxcompute(ODPS)-DataWorks平台,去掉代码注释即可#coding:utf-8 # from odps.udf…...
【R语言基础】如何更新R版本
文章目录 概要流程细节具体步骤 概要 提示:由于软件包的更新,所以需要更新R至新版本 流程细节 查看当前R版本 R.version下载更新包:installr install.packages("installr")library(installr)跟着向导一步步执行安装 具体步骤 …...

Python知识点10---函数
提前说一点:如果你是专注于Python开发,那么本系列知识点只是带你入个门再详细的开发点就要去看其他资料了,而如果你和作者一样只是操作其他技术的Python API那就足够了。 Python的函数和Scala的函数很像,语法很简单,注…...

有哪些挣钱软件一天能赚几十元?盘点十个能长期做下去的挣钱软件
在这个信息爆炸的时代,每个人都在寻找快速赚钱的秘诀。很多人做兼职副业的目标并不是获得很大的成功,大部分人一天能赚几十就心满意足了。 今天,我要带你一探究竟,揭秘那些能让你日赚几十元的挣钱软件。准备好了吗?让我…...

CentOS7安装MySQL教程
第一章 检查是否安装了Mysql 1.1 yum检查 yum list installed | grep mysql 1.2 安装则直接删除 yum remove xxx 1.3 rpm检查 rpm -qa | grep -i mysql # 有则直接删除 rpm -e --nodeps xxx 第二章 正式安装MySQL 2.1 yum安装,下载mysql wget --no-check-ce…...

师彼长技以助己(3)逻辑思维
师彼长技以助己(3)逻辑思维 前言 上一篇文章进行了工程思维和产品思维的测试,并介绍了几个比较重要的产品思维模型。接下来本篇介绍工程思维。(注意产品思维并不代表产品经理思维,工程思维也并不代表工程师思维&…...

LeetCode:反转链表I
文章收录于LeetCode专栏 LeetCode地址 反转链表I 题目 给你单链表的头节点head,请你反转链表,并返回反转后的链表。 示例 1: #mermaid-svg-IYmD16EKuu3CZWwV {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size…...

oracle linux7安装oracle11g0204
1、平时需要修改 /etc/redhat-release文件为Red Hat Enterprise Linux 7,这次不需要了。 2、关闭selinx nano /etc/selinux/config 改为disabled 3、nano /etc/hosts 修改解析 在oracle服务器中增加 /etc/hosts中一个对应 192.168.1.10 CLOUD-MC-SQL1 4、修改系统文件 /…...
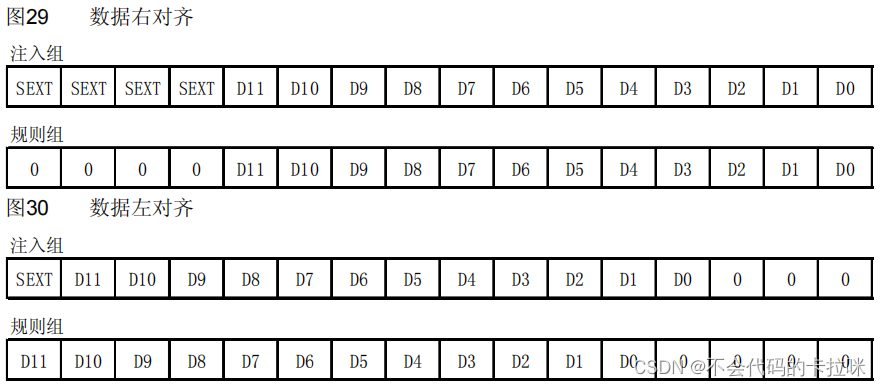
STM32--ADC
一、简介 *ADC(Analog-Digital Converter)模拟-数字转换器 *ADC可以将引脚上连续变化的模拟电压转换为内存中存储的数字变量,建立模拟电路到数字电路的桥梁 *12位逐次逼近型ADC,1us转换时间 *输入电压范围:0~3.3V&…...

【TB作品】msp430f149单片机,读取ds18b20温度,显示到数码管,串口发送温度到电脑
功能 msp430f149单片机 读取ds18b20温度,显示到数码管,串口发送温度到电脑 部分程序 /************************************************* * 程序功能:用DS18B20测量室温并在数码管上显示。 * --------------------------------------…...

vue组合式和选项式
Vue中的组合式(Composition API)和选项式(Options API)是两种不同的编写组件逻辑的方法。 组合式API(Composition API): 使用函数来定义组件逻辑,可以更灵活地重用和组合逻辑。使用setup函数作为组件的入口点,在这里可以访问pro…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...
