「动态规划」买卖股票的最佳时机
力扣原题链接,点击跳转。
给定一个整数数组prices,prices[i]表示股票在第i天的价格。你最多完成2笔交易。你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。设计一个算法计算最大利润。
我们用动态规划的思想来解决这个问题。首先确定状态表示。我们用f和g分别表示「买入」和「卖出」状态(处于「买入」状态时,手里有股票;处于「卖出」状态时,手里没有股票)。用i表示第i天结束时的状态。用j表示当前完成了j笔交易。也就是说,用f[i][j]表示在第i天结束时,处于「买入」状态下,完成了j笔交易,此时的最大利润;用g[i][j]表示在第i天结束时,处于「卖出」状态下,完成了j笔交易,此时的最大利润。
接下来推导状态转移方程。首先考虑f[i][j],如果第i-1天结束时处于「买入」状态,那么需要在第i天「持有股票」,就能在第i天结束时依然处于「买入」状态,由于「持有股票」并不会改变完成的交易次数,也不会改变利润,所以此时f[i][j]=f[i-1][j];如果第i-1天结束时处于「卖出」状态,那么需要在第i天「买入股票」,就能在第i天结束时处于「买入」状态,由于「买入股票」并不会改变完成的交易次数,但是会使利润减少第i天的股票价格,所以此时f[i][j]=g[i-1][j]-prices[i]。由于要求的是最大利润,所以f[i][j]=max(f[i-1][j],g[i-1][j]-prices[i])。
接着考虑g[i][j],如果第i-1天结束时处于「买入」状态,那么需要在第i天「卖出股票」,就能在第i天结束时处于「卖出」状态,由于「卖出股票」后就完成了一次完整的交易,所以在第i-1天结束时的交易次数会比第i天结束时的交易次数少1,即第i-1天结束时的交易次数是j-1,同时「卖出股票」会使利润增多第i天的股票价格,所以此时g[i][j]=f[i-1][j-1]+prices[i];如果第i-1天结束时处于「卖出」状态,那么需要在第i天「观望」,就会在第i天结束时依然处于「卖出状态」,而「观望」并不会改变交易次数和利润,所以此时g[i][j]=g[i-1][j]。由于要求的是最大利润,所以g[i][j]=max(f[i-1][j-1]+prices[i],g[i-1][j])。
接下来考虑初始化的问题。再次观察状态转移方程:f[i][j]=max(f[i-1][j],g[i-1][j]-prices[i]),g[i][j]=max(f[i-1][j-1]+prices[i],g[i-1][j])。由于f[i][j]和g[i][j]都会依赖于i-1,所以初始化2个表的最上面一行。注意到j的取值范围是[0,2],故需要初始化的坐标有:(0,0)、(0,1)和(0,2)。不过,(0,1)和(0,2)说明在第0天结束时已经至少完成了1笔交易,也就是说,会在第0天「买入后立刻卖出股票」,这种操作是没有意义的,因为浪费了交易次数。所以,为了让(0,1)和(0,2)的值不影响取max的结果,应该把这两个位置初始化为-∞,即-0x3f3f3f3f,注意不是INT_MIN,防止计算g[i-1][j]-prices[i]时溢出。所以,现在只需要考虑f[0][0]和g[0][0]。其中f[0][0]表示在第0天结束时处于「买入」状态,只需要在第0天「买入股票」,即f[0][0]=-prices[0];g[0][0]表示在第0天结束时处于「卖出」状态,只需要在第0天「观望」,即g[0][0]=0。
还有另一个地方有可能越界。注意到g[i][j]=max(f[i-1][j-1]+prices[i],g[i-1][j]),会依赖于j-1,所以理论上还需要初始化g表的最左边一列。但是这么做的话,会让f表和g表对应不上,导致细节问题更难处理。所以我们采取另一种方法。j代表的是交易次数,之所以j-1有可能越界,是因为这样算出来的交易次数是-1。既然不存在交易次数是-1的情况,我们只需要判断一下,如果j-1≥0,才计算g[i][j]=max(f[i-1][j-1]+prices[i],g[i-1][j]),否则g[i][j]=g[i-1][j]即可。这样,就不存在越界的风险了。
填表时应从上往下填每一行,每一行从左往右填,且f表和g表同时填。最终应返回g表的最后一行的最大值,这是因为要想获取最大利润,就一定要在最后一天结束时处于「卖出」状态,且不确定此时的交易次数。我们来分析一下dp表的规模。由于没有加上虚拟节点,所以行数应与实际天数相同,即prices的元素个数n;由于j的所有可能取值是0、1和2,所以有3列。综上,f表和g表的大小均为n×3。
class Solution {
public:int maxProfit(vector<int>& prices) {const int INF = 0x3f3f3f3f;int n = prices.size();// 创建dp表vector<vector<int>> f(n, vector<int>(3, -INF));auto g = f;// 初始化f[0][0] = -prices[0];g[0][0] = 0;// 填表for (int i = 1; i < n; i++){for (int j = 0; j < 3; j++){f[i][j] = max(f[i-1][j], g[i-1][j] - prices[i]);g[i][j] = g[i-1][j];if (j - 1 >= 0)g[i][j] = max(g[i][j], f[i-1][j-1] + prices[i]);}}// 求g表最后一行的最大值return *max_element(g[n-1].begin(), g[n-1].end());}
};这道题还有个终极版本:力扣原题链接,点击跳转。
把限定的交易次数从2次改为k次,其余条件不变,求最大利润。
分析思路完全一样。状态表示和状态转移方程不变。初始化方式不变,依然是最上面一行除了f[0][0]=-prices[0]和g[0][0]=0之外都初始化为-∞。填表顺序不变。最后依然是返回g表最后一行的最大值。只有表的规模从n×3变为了n×(k+1)。
代码的话,只需要把上道题的代码的3修改为k+1即可。事实上,上道题就是本题中k=2时的特殊情况。除此之外,还有一个点值得优化,最多的交易次数一定不会超过总天数的一半,比如总天数是10天,那么最多交易5次;总天数是9天,那么最多交易4次。
class Solution {
public:int maxProfit(int k, vector<int>& prices) {const int INF = 0x3f3f3f3f;int n = prices.size();// 交易次数不会超过总天数的一半k = min(k, n/2);// 创建dp表vector<vector<int>> f(n, vector<int>(k+1, -INF));auto g = f;// 初始化f[0][0] = -prices[0];g[0][0] = 0;// 填表for (int i = 1; i < n; i++){for (int j = 0; j < k+1; j++){f[i][j] = max(f[i-1][j], g[i-1][j] - prices[i]);g[i][j] = g[i-1][j];if (j - 1 >= 0)g[i][j] = max(g[i][j], f[i-1][j-1] + prices[i]);}}// 求g表最后一行的最大值return *max_element(g[n-1].begin(), g[n-1].end());}
};相关文章:

「动态规划」买卖股票的最佳时机
力扣原题链接,点击跳转。 给定一个整数数组prices,prices[i]表示股票在第i天的价格。你最多完成2笔交易。你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。设计一个算法计算最大利润。 我们用动态规划的思想来解决…...

Java 并发编程面试二
目录 一、并发编程三要素? 二、实现可见性的方法有哪些? 三、多线程的价值? 四、创建线程的有哪些方式? 五、创建线程的三种方式的对比? 六、Java 线程具有五中基本状态 七、什么是线程池?有哪几种创建方式 八、四种线程池的创建 九、线程池的优点? 十、常用的…...

成功解决“ModuleNotFoundError: No Module Named ‘utils’”错误的全面指南
成功解决“ModuleNotFoundError: No Module Named ‘utils’”错误的全面指南 在Python编程中,遇到ModuleNotFoundError: No Module Named utils这样的错误通常意味着Python解释器无法找到名为utils的模块。这可能是由于多种原因造成的,比如模块确实不存…...
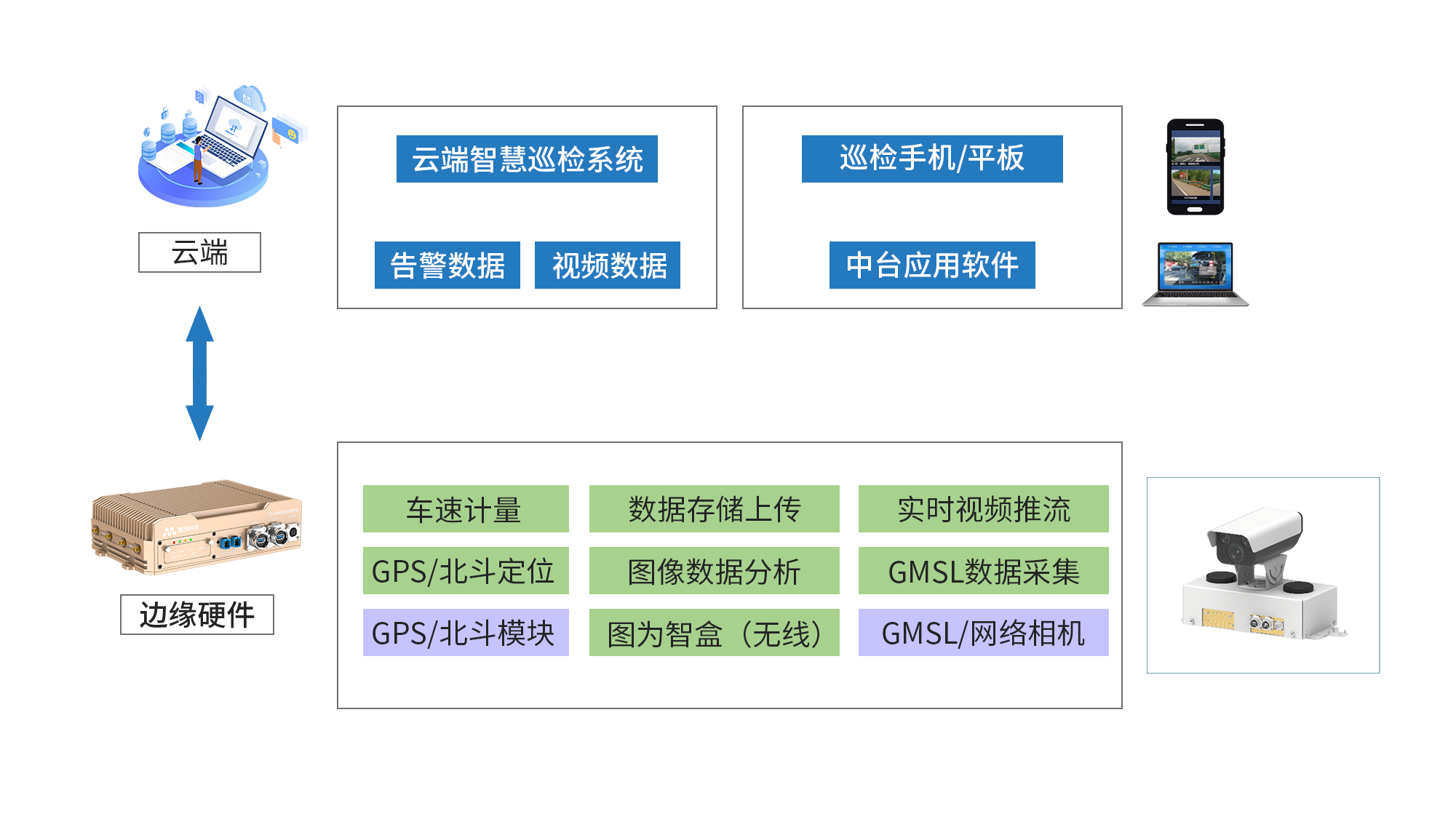
Nvidia Jetson/Orin +FPGA+AI大算力边缘计算盒子:公路智能巡检解决方案
项目背景 中国公路网络庞大,总里程超过535万公里,高速公路里程位居世界前列。面对基础设施存量的不断增长,公路养护管理已迈入“建管养并重”的新时代。随着养护支出的逐年攀升,如何提升养护效率、降低管理成本,成为亟…...

【Maxcompute】geohash转经纬度,经纬度转geohash,计算geohash九宫格
1.梳理、总结经纬度处理在Maxcompute平台上的实战应用,如geohash转经纬度,经纬度转geohash,计算geohash九宫格等。 2.欢迎批评指正,跪谢一键三连! 文章目录 1.部署代码1.部署代码 部署至Maxcompute(ODPS)-DataWorks平台,去掉代码注释即可#coding:utf-8 # from odps.udf…...
【R语言基础】如何更新R版本
文章目录 概要流程细节具体步骤 概要 提示:由于软件包的更新,所以需要更新R至新版本 流程细节 查看当前R版本 R.version下载更新包:installr install.packages("installr")library(installr)跟着向导一步步执行安装 具体步骤 …...

Python知识点10---函数
提前说一点:如果你是专注于Python开发,那么本系列知识点只是带你入个门再详细的开发点就要去看其他资料了,而如果你和作者一样只是操作其他技术的Python API那就足够了。 Python的函数和Scala的函数很像,语法很简单,注…...

有哪些挣钱软件一天能赚几十元?盘点十个能长期做下去的挣钱软件
在这个信息爆炸的时代,每个人都在寻找快速赚钱的秘诀。很多人做兼职副业的目标并不是获得很大的成功,大部分人一天能赚几十就心满意足了。 今天,我要带你一探究竟,揭秘那些能让你日赚几十元的挣钱软件。准备好了吗?让我…...

CentOS7安装MySQL教程
第一章 检查是否安装了Mysql 1.1 yum检查 yum list installed | grep mysql 1.2 安装则直接删除 yum remove xxx 1.3 rpm检查 rpm -qa | grep -i mysql # 有则直接删除 rpm -e --nodeps xxx 第二章 正式安装MySQL 2.1 yum安装,下载mysql wget --no-check-ce…...

师彼长技以助己(3)逻辑思维
师彼长技以助己(3)逻辑思维 前言 上一篇文章进行了工程思维和产品思维的测试,并介绍了几个比较重要的产品思维模型。接下来本篇介绍工程思维。(注意产品思维并不代表产品经理思维,工程思维也并不代表工程师思维&…...

LeetCode:反转链表I
文章收录于LeetCode专栏 LeetCode地址 反转链表I 题目 给你单链表的头节点head,请你反转链表,并返回反转后的链表。 示例 1: #mermaid-svg-IYmD16EKuu3CZWwV {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size…...

oracle linux7安装oracle11g0204
1、平时需要修改 /etc/redhat-release文件为Red Hat Enterprise Linux 7,这次不需要了。 2、关闭selinx nano /etc/selinux/config 改为disabled 3、nano /etc/hosts 修改解析 在oracle服务器中增加 /etc/hosts中一个对应 192.168.1.10 CLOUD-MC-SQL1 4、修改系统文件 /…...
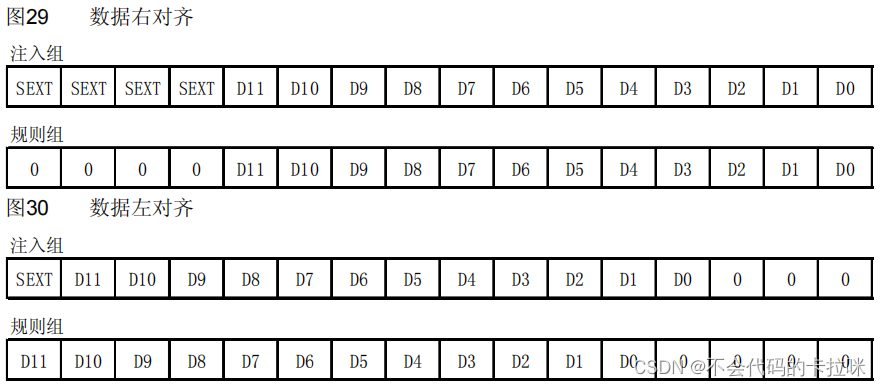
STM32--ADC
一、简介 *ADC(Analog-Digital Converter)模拟-数字转换器 *ADC可以将引脚上连续变化的模拟电压转换为内存中存储的数字变量,建立模拟电路到数字电路的桥梁 *12位逐次逼近型ADC,1us转换时间 *输入电压范围:0~3.3V&…...

【TB作品】msp430f149单片机,读取ds18b20温度,显示到数码管,串口发送温度到电脑
功能 msp430f149单片机 读取ds18b20温度,显示到数码管,串口发送温度到电脑 部分程序 /************************************************* * 程序功能:用DS18B20测量室温并在数码管上显示。 * --------------------------------------…...

vue组合式和选项式
Vue中的组合式(Composition API)和选项式(Options API)是两种不同的编写组件逻辑的方法。 组合式API(Composition API): 使用函数来定义组件逻辑,可以更灵活地重用和组合逻辑。使用setup函数作为组件的入口点,在这里可以访问pro…...

使用OpenCV创建全景图像
使用OpenCV创建全景图像 前言图像拼接策略创建全景图像相关链接前言 在本节中,我们将学习组合多个图像来创建全景图像。使用相机拍摄全景照片时,通常会拍摄多张照片,通过算法将这些图像中共同存在的元素(从左到右)映射到一张单独的图像中。为了执行图像的拼接,将利用 cv2 …...

Nios II 实现流水灯实验
Nios II 实现流水灯实验 一.硬件设计1.新建Quartus项目2. 设计Nios ii 二.软件设计 前言 实验目标: 学习 Quartus 、Platform Designer、Nios-II SBT 的基本操作;初步了解 SOPC 的开发流程,基本掌握 Nios-II 软核的定制方法;掌握 …...
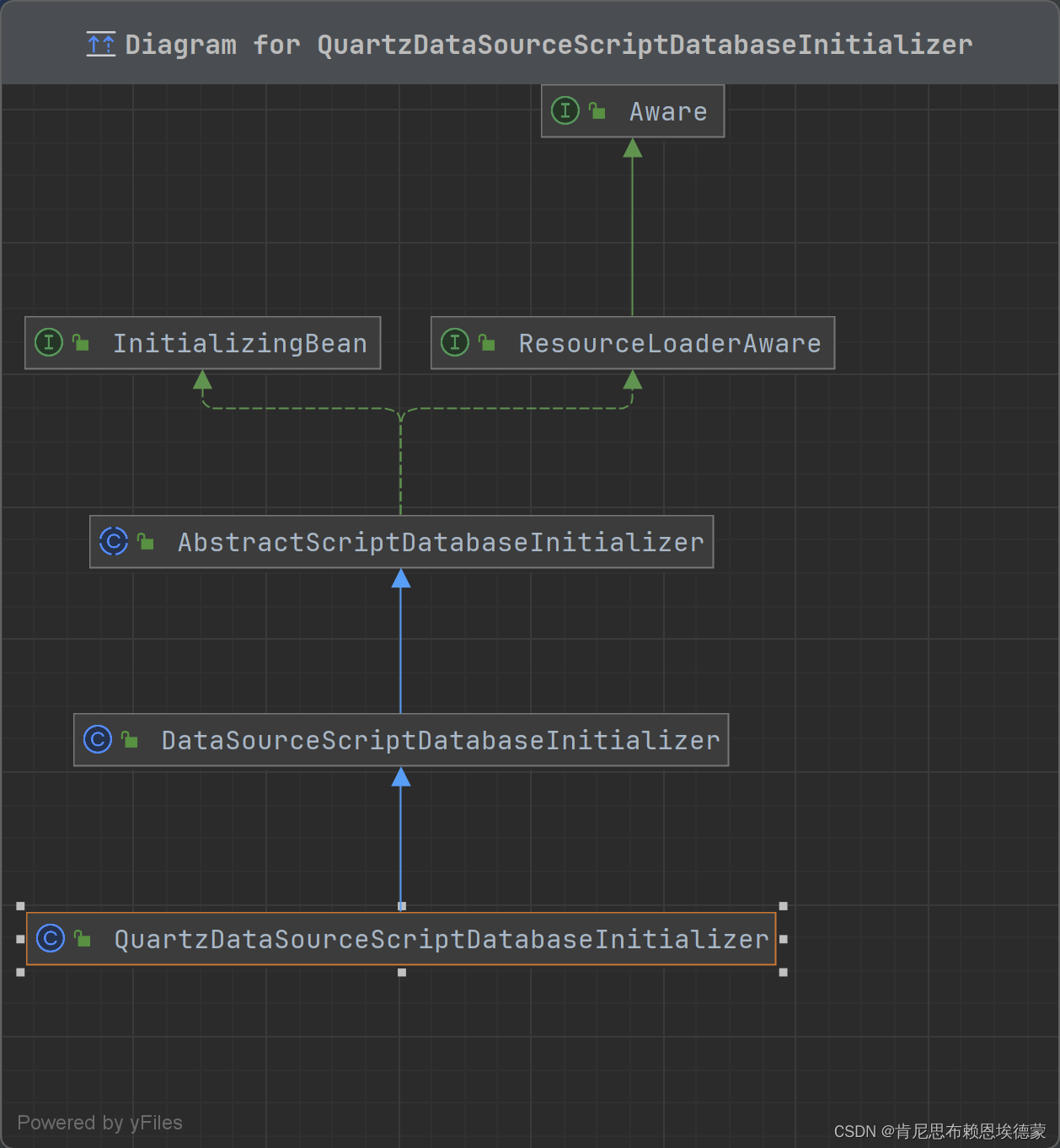
Spring boot 随笔 1 DatasourceInitializer
0. 为啥感觉升级了 win11 之后,电脑像是刚买回来的,很快 这篇加餐完全是一个意外:时隔两年半,再看 Springboot-quartz-starter 集成实现的时候,不知道为啥我的h2 在应用启动的时候,不能自动创建quartz相关…...

vue3_组件间通信方式
目录 一、父子通信 1.父传子( defineProps) 2.父传子(useAttrs) 3.子传父(ref,defineExpose ) 4.子传父(defineEmits) 5.子传父(v-model) …...

mysql的锁(全局锁)
文章目录 mysql按照锁的粒度分类全局锁概念:全局锁使用场景:全局锁备份案例: mysql按照锁的粒度分类 全局锁 概念: 全局锁就是对整个数据库实例加锁。MySQL 提供了一个加全局读锁的方法,命令是: Flush tables with…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...
