2021牛客OI赛前集训营-提高组(第三场) T3打拳
2021牛客OI赛前集训营-提高组(第三场)
题目大意
有2n2^n2n个选手参加拳击比赛,每个人都有一个实力,所有选手的实力用一个111到2n2^n2n的排列表示。
淘汰赛的规则是:每次相邻的两个选手进行比赛,实力值大的晋级到下一轮。
你的实力为111。为了取胜,你买通了mmm个选手,使得你与他们比赛时让你获胜。你想要获得冠军,且你战胜的选手的实力值构成的序列的最长上升子序列长度要≥k\geq k≥k。求满足条件的方案数。
题解
我们先考虑k=1k=1k=1的情况。
在这种情况下,我们只需要让叶子节点111到根节点的路径上所有的点都被已经收买的人占了,且满足这些点都是其子树的最大值。
将被收买的人按实力值从小到大排序。设fi,jf_{i,j}fi,j表示已经处理了前iii个被收买的人,jjj的二进制的每一位表示这个位置上是否有被收买的人占据。那么转移式如下
fi,j+2k+=fi,j×Cai−j−22k−1×(2k)!f_{i,j+2^k}+=f_{i,j}\times C_{a_i-j-2}^{2^k-1}\times (2^k)!fi,j+2k+=fi,j×Cai−j−22k−1×(2k)!,其中kkk为jjj的二进制位中为000的位。
Cai−j−22k−1C_{a_i-j-2}^{2^k-1}Cai−j−22k−1表示在实力在比aia_iai小的没有选过且不为111的ai−j−2a_i-j-2ai−j−2个选手中选2k−12^k-12k−1(因为已经确定了要有aia_iai,所以 要减1)个来组成kkk位置的子树。
因为子树内部可以任意排序,所以要乘上(2k)!(2^k)!(2k)!。
输出答案时,因为111的位置任意,所以要乘上2n2^n2n。
时间复杂度为O(2nnm)O(2^nnm)O(2nnm)。
code
#include<bits/stdc++.h>
using namespace std;
int n,m,k,a[25];
long long ans,yh[1005][1005],jc[1005],f[25][1<<15];
long long mod;
long long mi(long long t,long long v){if(!v) return 1;long long re=mi(t,v/2);re=re*re%mod;if(v&1) re=re*t%mod;return re;
}
void init(){yh[0][0]=1;for(int i=1;i<=1000;i++){yh[i][0]=yh[i][i]=1;for(int j=1;j<i;j++) yh[i][j]=(yh[i-1][j-1]+yh[i-1][j])%mod;}jc[0]=1;for(int i=1;i<=1000;i++) jc[i]=jc[i-1]*i%mod;
}
int main()
{scanf("%d%d%d%lld",&n,&m,&k,&mod);for(int i=1;i<=m;i++){scanf("%d",&a[i]);}sort(a+1,a+m+1);init();f[0][0]=1;for(int i=1;i<=m;i++){for(int j=0;j<(1<<n);j++){if(f[i-1][j]){f[i][j]=(f[i][j]+f[i-1][j])%mod;for(int t=0;t<n;t++){if(((j>>t)&1)==0&&a[i]>=j+(1<<t)+1){f[i][j+(1<<t)]=(f[i][j+(1<<t)]+f[i-1][j]*yh[a[i]-j-2][(1<<t)-1]%mod*jc[1<<t]%mod)%mod;}}}}}ans=f[m][(1<<n)-1]*mi(2,n)%mod;printf("%lld",ans);return 0;
}
再来考虑k≥1k\geq 1k≥1的情况。
我们可以考虑对LIS(最长上升子序列)的维护方法。
从小到大依次来维护每个数字的LIS,这个数字的LIS等于在其之前的所有数字的LIS的最大值+1。
比如四个数字{3,1,2,4}\{3,1,2,4\}{3,1,2,4},每次操作如下
{0,1,0,0}\{0,1,0,0\}{0,1,0,0}
{0,1,2,0}\{0,1,2,0\}{0,1,2,0}
{1,1,2,0}\{1,1,2,0\}{1,1,2,0}
{1,1,2,3}\{1,1,2,3\}{1,1,2,3}
我们可以暴力求出所有经过LIS过程后最大的LIS值能够≥k\geq k≥k的状态。状态的数量并不大,n=9n=9n=9的时候才不到120000120000120000。用这些状态来当之前状压的状态,这样即可求出答案。
时间复杂度为O(120000nm)O(120000nm)O(120000nm)。
code
#include<bits/stdc++.h>
#define N 120000
using namespace std;
int n,m,k,tot=0,t1=0,a[25],cnt[N+5];
long long ans=0,yh[1005][1005],jc[1005],f[25][N+5];
long long mod;
string pt[N+5],to[N+5];
map<string,int>z,re;
void dfs(string s,int now){if(!z[s]){z[s]=1;pt[++tot]=s;}else return;if(now==n) return;char c='0';for(int i=0;i<n;i++){if(s[i]=='0'){s[i]=c+1;dfs(s,now+1);s[i]='0';}else c=max(c,s[i]);}
// for(int i=0;i<n;i++){
// if(s[i]=='0'){
// string t=s;
// char c='0';
// for(int j=0;j<i;j++){
// c=max(c,s[j]);
// }
// t[i]=c+1;
// dfs(t,now+1);
// }
// }
}
void dd(){for(int i=1;i<=tot;i++){string s=pt[i];char c='0';for(int j=0;j<n;j++){if(s[j]=='0'){s[j]=c+1;c++;}else c=max(c,s[j]);}
// c='0';
// for(int j=0;j<n;j++) c=max(c,s[j]);if(c>='0'+k){to[++t1]=pt[i];re[pt[i]]=t1;}}for(int i=1;i<=t1;i++){for(int j=0;j<n;j++){if(to[i][j]!='0') cnt[i]|=(1<<j);}}
}
void init(){yh[0][0]=1;for(int i=1;i<=1000;i++){yh[i][0]=yh[i][i]=1;for(int j=1;j<i;j++) yh[i][j]=(yh[i-1][j-1]+yh[i-1][j])%mod;}jc[0]=1;for(int i=1;i<=1000;i++) jc[i]=jc[i-1]*i%mod;
}
long long mi(long long t,long long v){if(!v) return 1;long long re=mi(t,v/2);re=re*re%mod;if(v&1) re=re*t%mod;return re;
}
void gt(string &s,int t){char c='0';for(int i=0;i<t;i++) c=max(c,s[i]);s[t]=c+1;
}
int main()
{scanf("%d%d%d%lld",&n,&m,&k,&mod);for(int i=1;i<=m;i++){scanf("%d",&a[i]);}sort(a+1,a+m+1);string s;for(int i=1;i<=n;i++) s=s+'0';dfs(s,0);dd();init();f[0][1]=1;for(int i=1;i<=m;i++){for(int j=1;j<=t1;j++){if(f[i-1][j]){f[i][j]=(f[i][j]+f[i-1][j])%mod;string now=to[j],nxt;for(int t=0;t<n;t++){if(now[t]=='0'&&a[i]>=cnt[j]+(1<<t)+1){nxt=now;gt(nxt,t);f[i][re[nxt]]=(f[i][re[nxt]]+f[i-1][j]*yh[a[i]-cnt[j]-2][(1<<t)-1]%mod*jc[1<<t]%mod)%mod;}}}}}for(int i=1;i<=t1;i++){if(cnt[i]==(1<<n)-1){ans=(ans+f[m][i])%mod;}}ans=ans*mi(2,n)%mod;printf("%lld",ans);return 0;
}
相关文章:
 T3打拳)
2021牛客OI赛前集训营-提高组(第三场) T3打拳
2021牛客OI赛前集训营-提高组(第三场) 题目大意 有2n2^n2n个选手参加拳击比赛,每个人都有一个实力,所有选手的实力用一个111到2n2^n2n的排列表示。 淘汰赛的规则是:每次相邻的两个选手进行比赛,实力值大…...

C++面向对象编程之四:成员变量和成员函数分开存储、this指针、const修饰成员和对象
在C中,成员变量和成员函数是分开存储的,只有非静态成员变量才存储在类中或类的对象上。通过该类创建的所有对象都共享同一个函数#include <iostream> using namespace std;class Monster {public://成员函数不占对象空间,所有对象共享同…...
卷积神经网络(CNN)基础知识
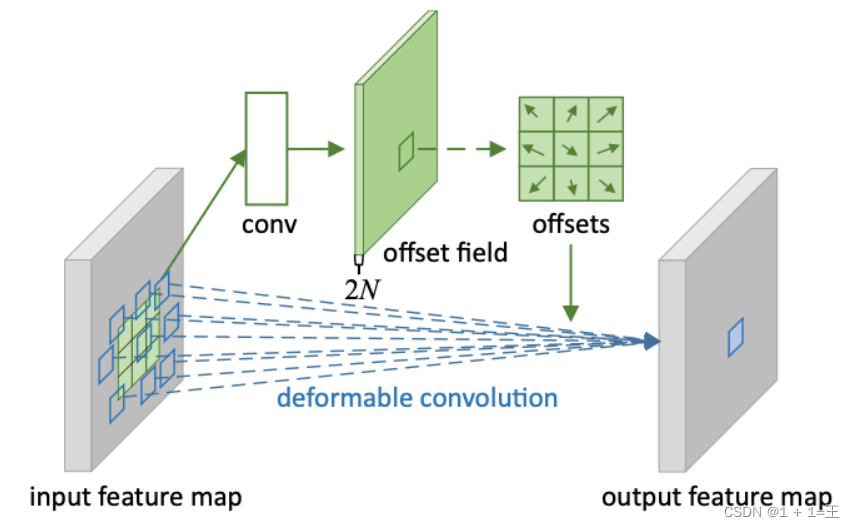
文章目录CNN的组成层卷积层卷积运算卷积的变种分组卷积转置卷积空洞卷积可变形卷积卷积层的输出尺寸和参数量CNN的组成层 在卷积神经⽹络中,⼀般包含5种类型的⽹络层次结构:输入层、卷积层、激活层、池化层和输出层。 输入层(input layer&a…...

opencv+python 常见图像预处理
import os import cv2 import numpy as np import pandas as pd from PIL import Image import matplotlib.pylab as plt """图像预处理"""#缩放 #灰度化 #二值化-otsu,自定义,自适应 #均值滤波 #中值滤波 #自定义滤波 #高斯/双倍滤波…...

如何实现一个单例模式
目录 前言 1.饿汉式 2.懒汉式 3.双重检测 4.静态内部类 5.枚举 总结: 前言 单例模式是我们日常开发过程中,遇到的最多的一种设计模式。通过这篇文章主要分享是实现单例的几种实现方式。 1.饿汉式 饿汉式的实现方式比较简单。在类加载的时候&#…...
传输线的物理基础(四):传输线的驱动和返回路径
驱动一条传输线对于将信号发射到传输线的高速驱动器,传输线在传输时间内的输入阻抗将表现得像一个电阻,相当于线路的特性阻抗。鉴于此等效电路模型,我们可以构建驱动器和传输线的电路,并计算发射到传输线中的电压。等效电路如下图…...

Java多态性
文章目录对象的多态性多态的理解举例7.2 多态的好处和弊端7.3 虚方法调用(Virtual Method Invocation)7.4 成员变量没有多态性7.5 向上转型与向下转型7.6 为什么要类型转换呢?7.7 如何向上转型与向下转型7.8 instanceof关键字7.9 复习:类型转换7.10 练习…...

算法拾遗二十七之窗口最大值或最小值的更新结构
算法拾遗二十七之窗口最大值或最小值的更新结构滑动窗口题目一题目二题目三题目四滑动窗口 第一种:R,R右动,数会从右侧进窗口 第二种:L,L右动,数从左侧出窗口 题目一 arr是N,窗口大小为W&…...

【带你搞定第二、三、四层交换机】
01 第二层交换机 OSI参考模型的第二层叫做数据链路层,第二层交换机通过链路层中的MAC地址实现不同端口间的数据交换。 第二层交换机主要功能,就包括物理编址、错误校验、帧序列以及数据流控制。 因为这是最基本的交换技术产品,目前桌面…...

C++基础了解-22-C++ 重载运算符和重载函数
C 重载运算符和重载函数 一、C 重载运算符和重载函数 C 允许在同一作用域中的某个函数和运算符指定多个定义,分别称为函数重载和运算符重载。 重载声明是指一个与之前已经在该作用域内声明过的函数或方法具有相同名称的声明,但是它们的参数列表和定义…...
BatchNormalization
目录 Covariate Shift Internal Covariate Shift BatchNormalization Q1:BN的原理 Q2:BN的作用 Q3:BN的缺陷 Q4:BN的均值、方差的计算维度 Q5:BN在训练和测试时有什么区别 Q6:BN的代码实现 Covariate Shift 机器学习中&a…...

vue 中安装插件实现 rem 适配
vue 中实现 rem 适配vue 项目实现页面自适应,可以安装插件实现。 postcss-pxtorem 是 PostCSS 的插件,用于将像素单元生成 rem 单位。 autoprefixer 浏览器前缀处理插件。 amfe-flexible 可伸缩布局方案替代了原先的 lib-flexible 选用了当前众多浏览…...
Hadoop学习
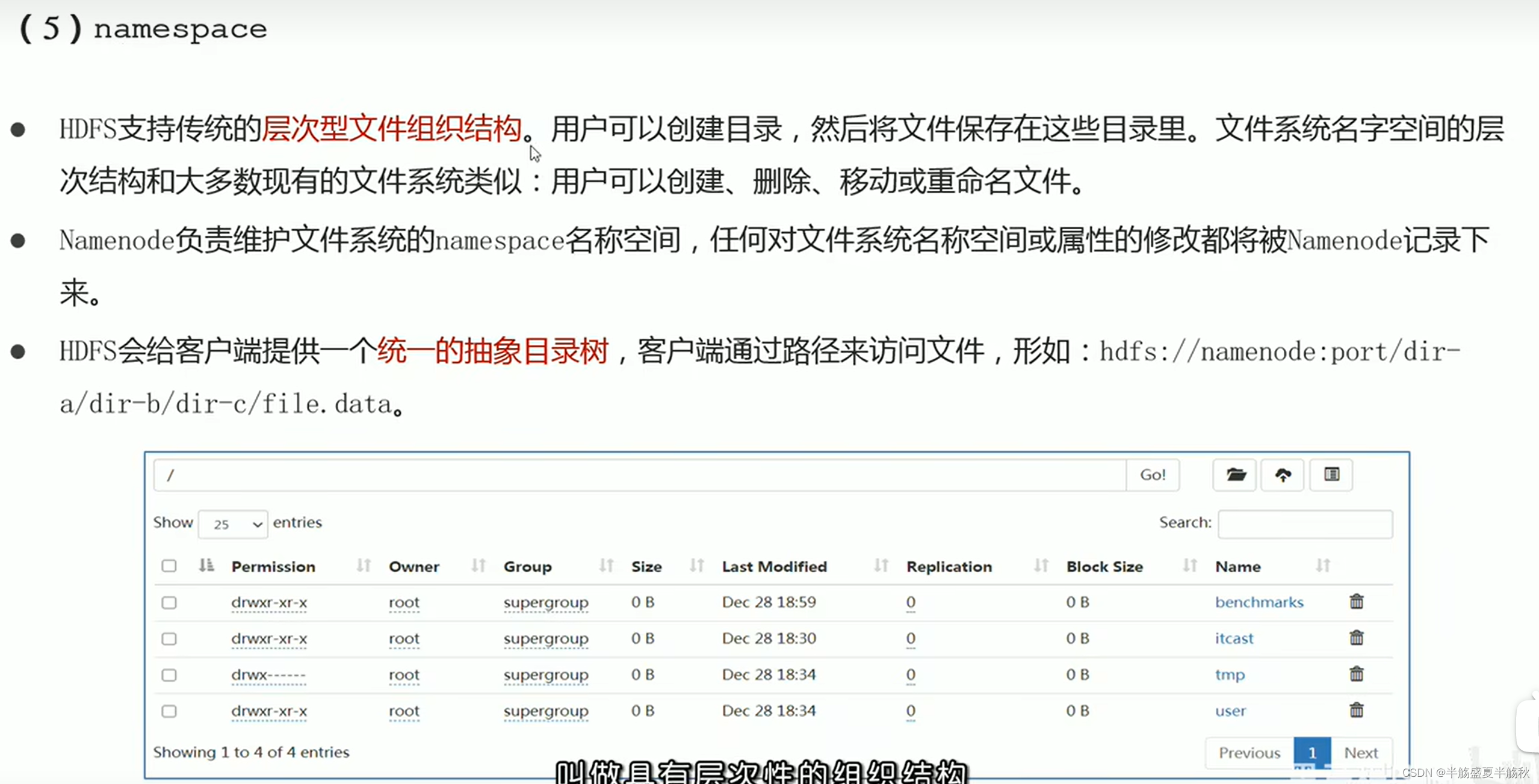
1.分布式与集群 hosts文件: 域名映射文件 2.Linux常用命令 ls -a:查看当前目录下所有文件mkdir -p:如果没有对应的父文件夹,会自动创建rm -rf:-f:强制删除 -r:递归删除cp -r:复制文…...

Golang反射源码分析
在go的源码包及一些开源组件中,经常可以看到reflect反射包的使用,本文就与大家一起探讨go反射机制的原理、学习其实现源码 首先,了解一下反射的定义: 反射是指计算机程序能够在运行时,能够描述其自身状态或行为、调整…...

Qt之悬浮球菜单
一、概述 最近想做一个炫酷的悬浮式菜单,考虑到菜单展开和美观,所以考虑学习下Qt的动画系统和状态机内容,打开QtCreator的示例教程浏览了下,大致发现教程中2D Painting程序和Animated Tiles程序有所帮助,如下图所示&a…...
易优cms attribute 栏目属性列表
attribute 栏目属性列表 attribute 栏目属性列表 [基础用法] 标签:attribute 描述:获取栏目的属性列表,或者单独获取某个属性值。 用法: {eyou:attribute typeauto} {$attr.name}:{$attr.value} {/eyou:attri…...

表格中的table-layout属性讲解
表格中的table-layout属性讲解 定义和用法 tableLayout 属性用来显示表格单元格、行、列的算法规则。 table-layout有三个属性值:auto、fixed、inherit。 fixed:固定表格布局 固定表格布局与自动表格布局相比,允许浏览器更快地对表格进行布…...

【MFA】windows环境下,使用Montreal-Forced-Aligner训练并对齐音频
文章目录一、安装MFA1.安装anaconda2.创建并进入虚拟环境3.安装pyTorch二、训练新的声学模型1.确保数据集的格式正确2.训练声音模型-导出模型和对齐文件3.报错处理1.遇到类似: Command ‘[‘createdb’,–host‘ ’, ‘Librispeech’]’ returned non-zero exit sta…...

C语言实验小项目实例源码大全订票信息管理系统贪吃蛇图书商品管理网络通信等
wx供重浩:创享日记 对话框发送:c项目 获取完整源码源文件视频讲解环境资源包文档说明等 包括火车订票系统、学生个人消费管理系统、超级万年历、学生信息管理系统、网络通信编程、商品管理系统、通讯录管理系统、企业员工管理系统、贪吃蛇游戏、图书管理…...

电脑图片损坏是怎么回事
电脑图片损坏是怎么回事?对于经常使用电脑的我们,总是会下载各种各样的图片,用于平时的使用中。但难免会遇到莫名其妙就损坏的图片文件,一旦发生这种情况,要如何才能修复损坏的图片呢?下面小编为大家带来常用的修复方…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...
