【刷题笔记】--二分-P2440 木材加工
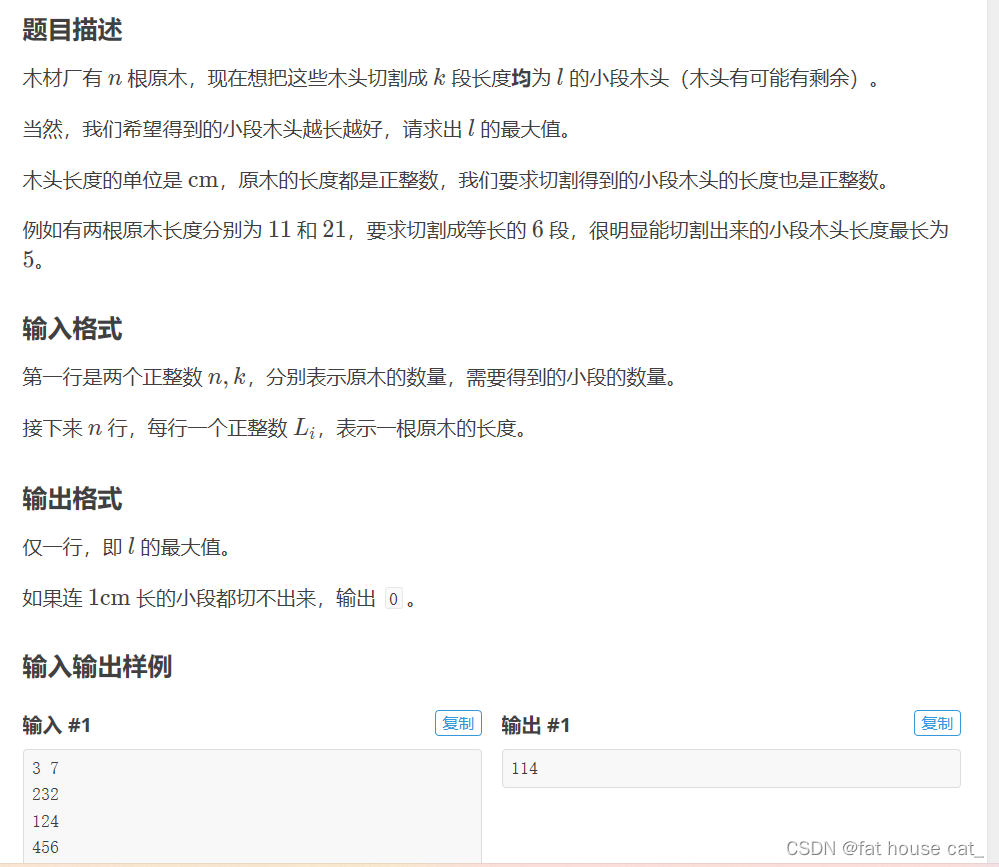
题目:
思路:
先在所有树中找到最长的树,从 1 到 这个最长的树的长度 的所有数作为二分查找的值,让每棵树除这个值,表示可以切出几段出来,累加在一起得到s,s表示一共有几段。s与k比较,如果s==k,表示找到了切出每段的长度,但此时并不能就结束了,也有可能这个长度再长一点,也可以切出我们要的k段。
一开始写的错误代码:
#include<stdio.h>
int cmp(const void *a,const void *b){return *(int *)a-*(int *)b;
}
int main(){long long n,k;//n是指有n根原木,k是指切出k段 scanf("%lld %lld",&n,&k);int i;long long tree[1000005];for(i=0;i<n;i++){scanf("%lld",&tree[i]);}long long sum=0;for(i=0;i<n;i++){sum+=tree[i];} if(sum/k==0){printf("0");return 0;} qsort(tree,n,sizeof(tree[0]),cmp);long long left=1;long long right=tree[n-1];long long s=0;while(left<=right){s=0;long int mid=(left+right)/2;for(i=0;i<n;i++){s+=tree[i]/mid;}if(s>k){left=mid+1;}else if(s<k){right=mid-1;}else{printf("%lld",mid);break;}}return 0;
}错就错在了我把s==k的情况单独分出来,然后就break了。
正确的代码:
#include<stdio.h>
int max(int a,int b){if(a>b){return a;}else{return b;}
}
int main(){long long n,k;//n是指有n根原木,k是指切出k段 scanf("%lld %lld",&n,&k);int i;long long tree[1000005];long long max1=0;for(i=0;i<n;i++){scanf("%lld",&tree[i]);max1=max(tree[i],max1);}long long sum=0;for(i=0;i<n;i++){sum+=tree[i];} if(sum/k==0){printf("0");return 0;} long long left=1;long long right=max1;long long s=0;long long ans;while(left<=right){s=0;long long mid=(left+right)/2;for(i=0;i<n;i++){s+=tree[i]/mid;}if(s>=k){left=mid+1;}else{right=mid-1;}}printf("%lld",left-1);return 0;
}我们来重点分析这一段:
if(s>=k){left=mid+1;}else{right=mid-1;}printf("%lld",left-1);其实这种只写两种情况,很好理解,当找到s==k时,left会继续往右走,跨过当前我们找到的这个mid的值, 如果右边还存在可以满足我们要的s==k的情况,就会继续进入s>=k的条件下,然后left又会跨过我们要的mid的值,而如果右边范围不存在s==k,或者s>k也不成立,那么就只会一直进入right=mid-1;此时,left一直没动,right一直在往左移,直到right移到了left左边,循环结束,输出left-1,就是我们当时要的mid值。
有个问题需要注意的是,为什么这个s==k的情况要连在s>k一起写,而不是和s<k,因为当找到s==k的情况时,我们还要再找有没有就是可以切出更长段的k段,所以肯定是要往数值大的方向去找,所以执行的语句是left=mid+1;而不是right=mid-1;
其实也可以拆开写:
if(s>k){left=mid+1;}else if(s<k){right=mid-1;}else{left=mid+1;} printf("%lld",left-1);
相关文章:

【刷题笔记】--二分-P2440 木材加工
题目: 思路: 先在所有树中找到最长的树,从 1 到 这个最长的树的长度 的所有数作为二分查找的值,让每棵树除这个值,表示可以切出几段出来,累加在一起得到s,s表示一共有几段。s与k比较…...

netstat 命令详解
文章目录简介命令格式常用选项常用命令查询进程所占用的端口号查看端口号的使用情况显示所有连接和监听端口并显示每个连接相关的进程ID显示UDP、TCP协议的连接的统计信息并显示每个连接相关的进程 ID显示所有已建立的连接显示每个进程的连接数显示每个IP地址的连接数显示每种类…...
分布式 微服务
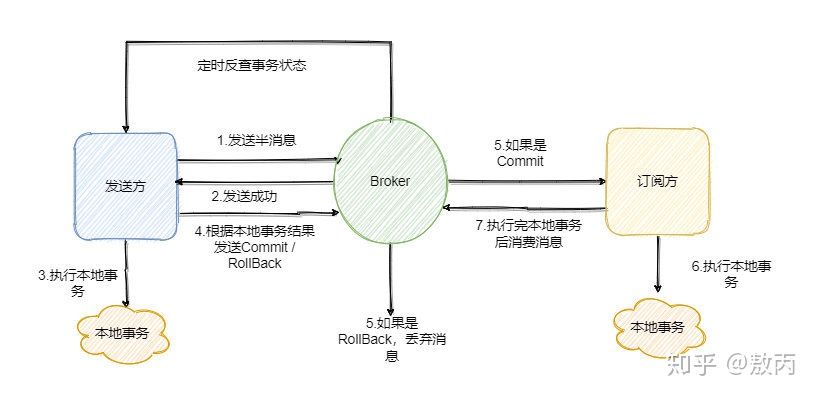
微服务学习 soa和微服务 业务系统实施服务化改造之后,原本共享的业务被拆分形成可复用的服务,可以在最大程度上避免共享业务的重复建设、资源连接瓶颈等问题。那么被拆分出来的服务是否也需要以业务功能为维度来进行拆分和独立部署,以降低业…...
Day912.多环境配置隔离 -SpringBoot与K8s云原生微服务实践
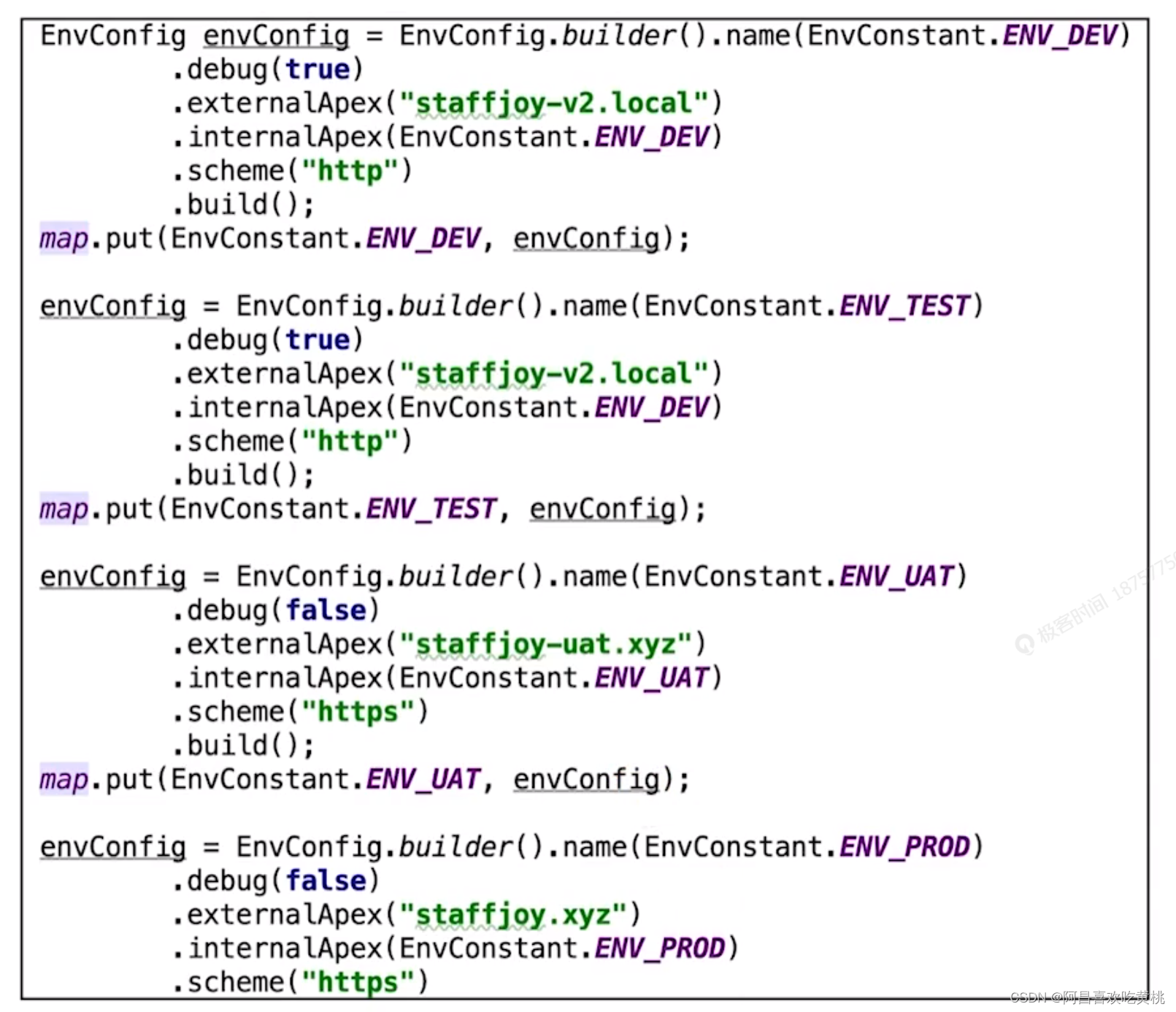
多环境配置隔离 Hi,我是阿昌,今天学习记录的是关于多环境配置隔离的内容。 多环境支持,是现在互联网开发研发和交付的主流基本需求。通过规范多环境配置可以规范开发流程,并同时提示项目的开发质量和效率等。 一个公司应该规范…...
Imx6ull交叉编译nginx
Imx6ull交叉编译nginx 需要下好的包 Nginx(下载压缩包源码) nginx-rtmp-module(可以下载压缩包源码也可以 git clone https://github.com/arut/nginx-rtmp-module.git) pcre(下载源码) zlib(下载源码) openssl(下载源…...

阿里云短信验证
1.了解阿里云用户权限操作 需要通过个人账户获得 授权码(id、密码),再通过这些信息获得服务 阿里云网址 :https://www.aliyun.com/ 1.登陆阿里云服务器2.进入个人账号然后点击 AccessKey 管理3.创建用户组4.添加用户组权限&…...
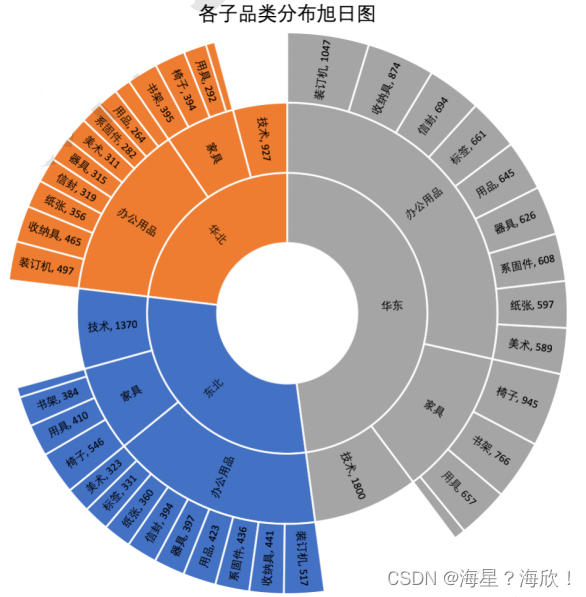
Excel常用可视化图表
目录柱状图与条形图折线图饼图漏斗图雷达图瀑布图及甘特图旭日图组合图excel图表:柱状数据条、excel热力图、mini图可视化工具的表现形式:看板、可视化大屏、驾驶舱 柱状图与条形图 条形图是柱状图的转置 类别: 单一柱状图:反映…...

虹科分享 | 网络流量监控 | 数据包丢失101
什么是数据包? 数据包是二进制数据的基本单位,在网络连接的设备之间编号和传输,无论是在本地还是通过互联网。一旦数据包到达其目的地,它就会与其他数据包一起按编号重新组合,回到最初传输的较大消息中。 数据包是我们…...

毕设常用模块之舵机介绍以及使用方法
舵机 舵机是一种位置伺服的驱动器,主要是由外壳、电路板、无核心马达、齿轮与位置检测器所构成。其工作原理是由接收机或者单片机发出信号给舵机,其内部有一个基准电路,产生周期为 20ms,宽度为 1.5ms 的基准信号,将获…...

残酷现实:大部分的App小程序,日活<100
残酷现实:99%的APP小程序,日活<100 日活跃用户数量(DAU)是一个核心指标 Daily Active Users 互联网的难度系数一路拉高 只有流过血的战士,才能意识到战场的残酷 趣讲大白话:赵本山小品台词, 残酷的现实已直逼我心理…...
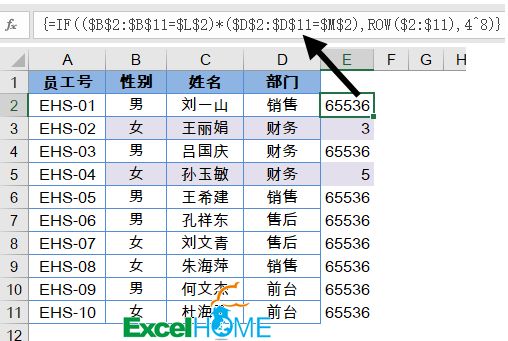
excel 一对多数据查询公式 经典用法
所谓一对多,就是符合某个指定条件的有多个结果,要把这些结果都提取出来。 下面咱们就说说一对多查询的典型用法,先看数据源: A~D列是一些员工信息,要根据F2单元格指定的学历,提取出所有“本科”的人员姓名…...
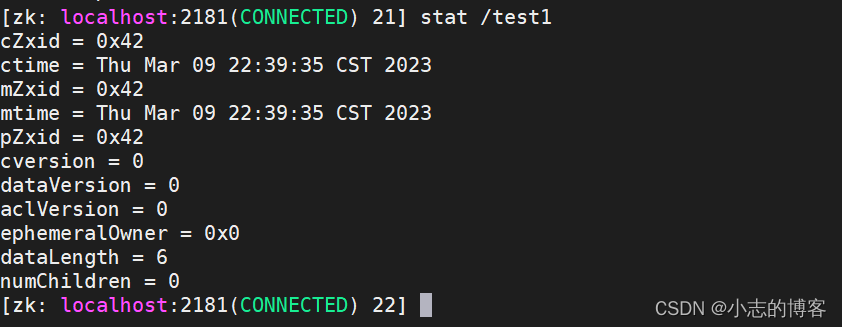
Zookeeper3.5.7版本——客户端命令行操作(节点删除与查看)
目录一、节点删除示例1.1、节点删除1.2、递归节点删除二、查看节点状态示例一、节点删除示例 1.1、节点删除 在客户端上创建 test 节点,并查看该节点 [zk: localhost:2181(CONNECTED) 5] create /test "123456"删除 test 节点,并查看该节点 […...

一句话设计模式6:享元模式
享元模式:局部单例模式。 文章目录 享元模式:局部单例模式。前言一、享元模式的作用二、如何实现享元模式总结前言 享元模式其实很简单,但是如果用好,确实可以达到减少内存,事半功倍的效果;适合 系统要创建大量相似对象,相同对象等; 一、享元模式的作用 1 享元模式可以解决对象…...
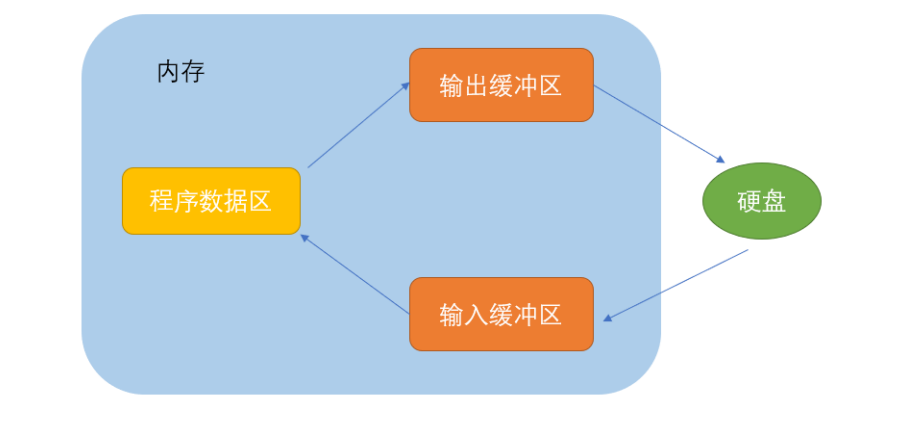
【C语言进阶】文本与二进制操作文件,优化通讯录。
前言:上篇文章,我们已经学习了有关本地磁盘文件的常用文件操作,已经能够对本地文件进行调用与读写。我们磁盘中还存在着一些内容用二进制存储的文件,这也就是我们今天将要讲解的内容。一、文本文件与二进制文件根据数据的组织形式…...
CleanMyMac X4.20最新Mac系统垃圾清理工具
CleanMyMac X是一款Mac系统垃圾清理工具,可以清除Mac系统多余的语言包、系统缓存、应用程序、PowerPc软件运行库等,是硬盘瘦身的好工具。在面对一款多功能型的软件时,复杂的操作面板是最容易让人头疼的,好在 CleanMyMac 一直以来都原生支持简体中文语言&…...
为什么做知识管理,就想选择Baklib呢?
随着科技的不断发展,知识管理已经成为现代企业不可或缺的一个重要组成部分。由于信息化快速发展,企业每天都会产生大量的数据和信息,如何高效地获取、整理和利用这些信息已经成为了企业成功的关键因素之一。为了更好地管理企业知识࿰…...
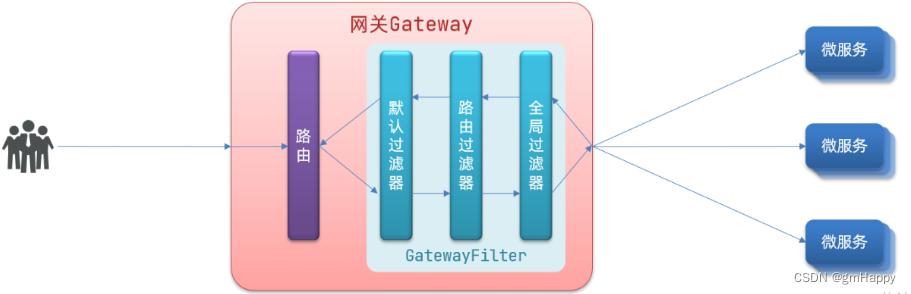
Spring Cloud融合gateway自带GatewayFilter使用 | Spring Cloud 15
一、Spring Cloud Gateway内置GatewayFilter 路由过滤器允许以某种方式修改传入的 HTTP 请求或传出的 HTTP 响应。路由过滤器的范围是特定路由。Spring Cloud Gateway 包括许多内置的 GatewayFilter 工厂。 官网地址:https://docs.spring.io/spring-cloud-gateway…...

SVN 版本控制软件
SVN 版本控制软件 属于C/S结构软件(客户端与服务端) 服务端软件:VisualSVN 网址:Downloads | VisualSVN 下载好:VisualSVN-Server-5.1.3-x64.msi 客户端软件:TortoiseSVN 网址:http://tor…...
全流程基于最新导则下的生态环境影响评价技术方法及图件制作与案例
目录 专题一、生态环境影响评价框架及流程 专题二、基于遥感解译的土地利用现状图的编制 专题三、生物多样性测定及R语言分析 专题四、植被类型及植被覆盖度图的编制 专题五、生物量与净初级生产力测定:实测及模型 专题六、生态系统类型及服务价值评估 专题七…...

(蓝桥真题)分果果(动态规划)
题目链接:P8746 [蓝桥杯 2021 省 A] 分果果 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 样例1输入: 5 2 6 1 2 7 9 样例1输出: 0 样例2输入: 5 5 6 1 2 7 9 样例2输出: 2 分析:这道题的状态表…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...
