(蓝桥真题)分果果(动态规划)
题目链接:P8746 [蓝桥杯 2021 省 A] 分果果 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

样例1输入:
5 2
6 1 2 7 9样例1输出:
0样例2输入:
5 5
6 1 2 7 9样例2输出:
2分析:这道题的状态表示比较难想:首先我们先考虑一下有哪些东西需要维护:
1.当前分配到哪个小朋友
2.当前分配到的小朋友的糖果最小值
3.当前分配到的小朋友的糖果最大值
4.当前已经分配一次的糖果编号位置
5.当前已经分配两次的糖果编号位置
那么其中我们可以选择一个作为f数组的含义,其余的四个显然都需要枚举。我们可以考虑用f数组存储当前状态分配到的小朋友的糖果的最大值,那么我们就开始枚举剩余四个维度。
设f[i][j][k]表示第i个人取到的最后一个糖果编号是j,第i-1个人取到的最后一个糖果编号小于等于k时的最大重量的最小值
答案就是min(f[m][n][n]-mn),所以我们要在mn一定的情况下尽可能减少f数组的值
首先要枚举的就是分配到的小朋友的糖果的最小值mn,那么我们每次考虑给小朋友分配一段连续的糖果区间就要注意区间和不能小于mn。
那么f[i][j][k]应该怎么更新呢?
首先有f[i][j][k]=f[i][j][k-1],这个无需多言,由于f数组维护的最大值,那么从这个角度也可以看出随着k的增加f数组是非递增的
还有就是第i个人用了前i-1个人中已经分配两次糖果编号的后某个位置开始,不妨设为t
那么就有f[i][j][k]=max(f[i-1][k][t],s[j]-s[t]),s数组是前缀和
但是为了尽可能减少f数组的值,就要使得f[i-1][k][t]和s[j]-s[t]的值都尽可能小,我们可以发现,随着t的增大,这两个值都是在逐渐减小的,但是t也要有一个限制条件,就是因为我们给第i个人分配的糖果区间是[t,j],所以这个区间内的糖果总数是要大于等于最小值mn的,所以这块我们可以。
有小伙伴可能会有疑问,为什么不能是从前i-1个人中已经分配一次糖果编号的后一个位置开始呢?这个是包含在上述情况的,因为分配两次糖果编号的位置一定是小于分配一次糖果编号的位置的,所以我们从分配两次糖果编号的位置开始分配总有一次会使得编号位置大于分配一次糖果编号的位置,这个时候原来的分配一次编号的位置就变为了分配两次编号的位置了,那么也就变成上述情况了。
还有就是从上面的分析,我们可以发现每次从分配两次的编号后面的某个位置t开始继续分配,此次分配后的位置都是大于等于分配一次的编号的位置,有没有可能是小于第一次分配编号的位置呢?这个是不可能的,因为如果小于第一次编号分配的位置,那么说明上次分配的区间是包含本次分配的区间的,那么我们完全可以把这两次分配调整为相交但不包含的情况,这样两个区间的最大值一定会减少,由于答案是最大值减去最小值,所以对答案也只会更优
其他就是一些细节上的问题了,可以看下代码:
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
const int N=103;
int f[N][N][N],w[N],s[N];
/*
f[i][j][k]表示第i个人取到的最后一个糖果编号是j,第i-1
个人取到的最后一个糖果编号小于等于k时的最大重量的最小值
*/
bool vis[N*N];//vis[i]记录存在一段区间满足区间和为i
int main()
{int n,m;cin>>n>>m;for(int i=1;i<=n;i++){scanf("%d",&w[i]);s[i]=s[i-1]+w[i];for(int j=0;j<i;j++)vis[s[i]-s[j]]=true;}int ans=0x3f3f3f3f;for(int mn=1;mn*m<=2*s[n];mn++)//枚举重量最小值 {if(!vis[mn]) continue;//剪枝 memset(f,0x3f,sizeof f);f[0][0][0]=0;for(int i=1;i<=m;i++)//枚举当前更新状态for(int k=0;k<=n;k++)//枚举第i-1个人选的最后一个糖果编号{int id=0;//找到第i-2个人选的最后一个糖果编号for(int j=k;j<=n;j++)//第i个人选的最后一个糖果编号 { if(k>0) f[i][j][k]=f[i][j][k-1];if(s[j]<mn) continue;//每个人选取的最小重量不能小于mn//第i个人选的区间是[id+1,j]while(id<k&&s[j]-s[id]>mn) id++;if(s[j]-s[id]<mn) id--;f[i][j][k]=min(f[i][j][k],max(f[i-1][k][id],s[j]-s[id]));}}ans=min(ans,f[m][n][n]-mn); }printf("%d",ans);return 0;
}相关文章:

(蓝桥真题)分果果(动态规划)
题目链接:P8746 [蓝桥杯 2021 省 A] 分果果 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 样例1输入: 5 2 6 1 2 7 9 样例1输出: 0 样例2输入: 5 5 6 1 2 7 9 样例2输出: 2 分析:这道题的状态表…...
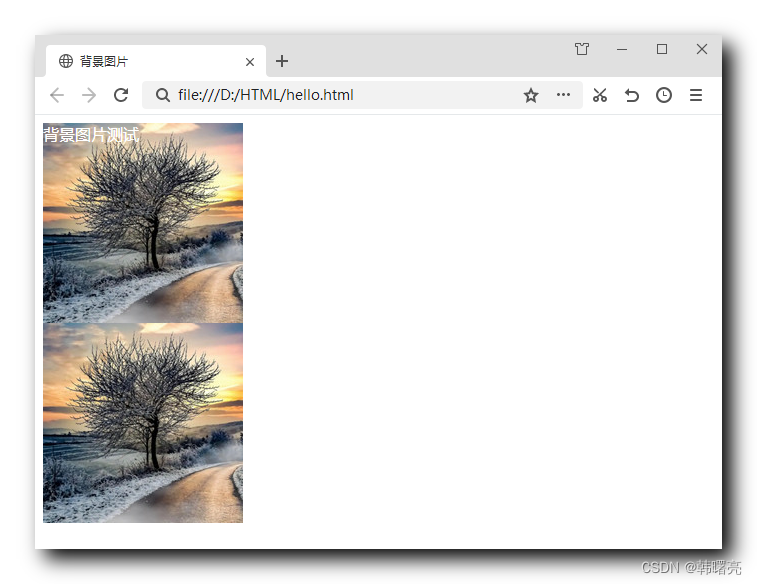
【CSS】CSS 背景设置 ① ( 背景颜色 | 背景图片 | 背景平铺 )
文章目录一、背景颜色1、语法说明2、代码示例二、背景图片1、语法说明2、代码示例三、背景平铺一、背景颜色 1、语法说明 CSS 的背景颜色样式语法 : 默认的背景颜色是 transparent 透明 ; background-color:颜色值;background-color 属性 可以 定义 文本颜色 , 其颜色值有三种…...
uniCloud基础使用
获取openID云函数use strict; exports.main async (event, context) > {//event为客户端上传的参数console.log(event : , event)// jscode2session 微信小程序登录接口,获取openidconst {code} event;// 云函数中如需要请求其他http服务,则使用uni…...

5、Elasticsearch优化
一、Elasticsearch集群配置 1、硬件选择 Elasticsearch的基础是 Lucene ,所有的索引和文档数据是存储在本地的磁盘中, 具体的路径可在 ES 的配置文件 ../config/elasticsearch.yml 中配置,如下:磁盘在现代服务器上通常都是瓶颈。…...

地质灾害防治单位资质
地质灾害危险性评估,是指在地质灾害易发区进行工程建设或者编制地质灾害易发区内的国土空间规划时,对建设工程或者规划区遭受山体崩塌、滑坡、泥石流、地面塌陷、地裂缝、地面沉降等地质灾害的可能性和建设工程引发地质灾害的可能性作出评估,…...
打怪升级之发送单个UDP包升级版
目标 1.message的输入由edit_control进行,需要捕获输入。 2.用户的主机地址和发送地址不一样,需要分别设置并绑定。 设计RC外观 必备组件:主机IP与端口,从机IP与端口,消息框,发送,连接按钮。…...

MyBatis开发
MyBatis开发入门搭建MyBatis框架开发环境在自己建的的项目建立个lib文件然后导入包3.两个jar包部署到项目中和为项目添加测试类库4.配置数据库mybatis-config.xml里面的配置:<?xml version"1.0" encoding"UTF-8"?> <!DOCTYPE config…...
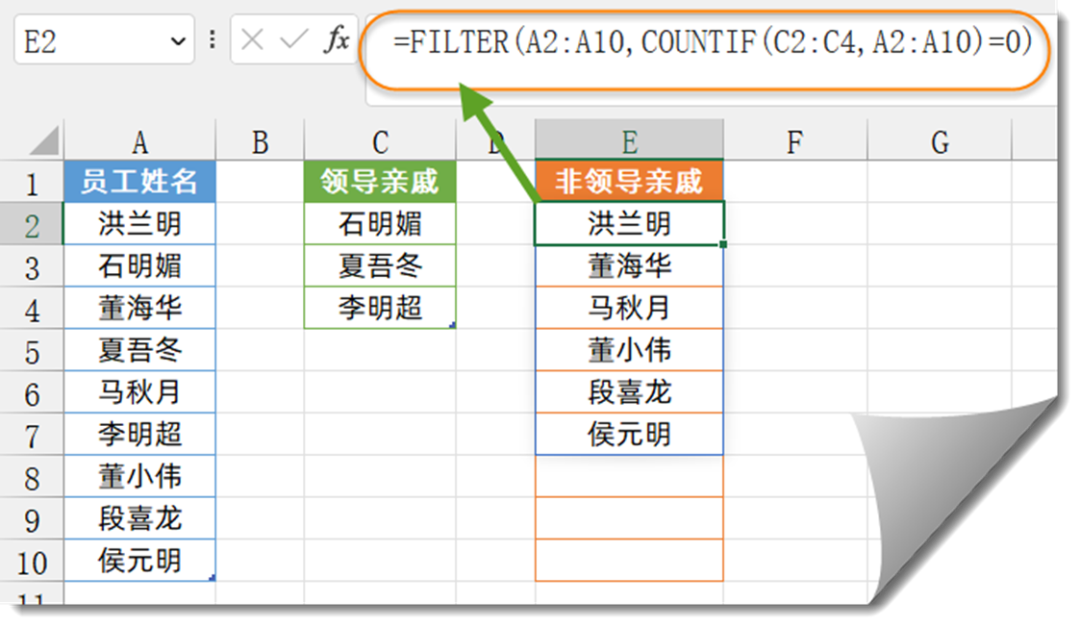
excel 数据查询,几个模式化公式请收好
1、一对多查询 所谓一对多,就是符合某个指定条件的有多个结果,要把这些结果都提取出来。 如下图所示,希望根据F2单元格中指定的部门,提取出左侧列表中“生产部”的所有人员姓名。 Excel 2019及以下版本:在H2单元格输…...

Prometheus MySQL 性能监控
一、 介绍 Prometheus 是一种开源的监控系统和时序数据库,旨在收集和处理大量数据并提供可视化、监控警报等功能。它支持多种语言、多种部署方式,并且非常灵活,而且社区支持非常活跃,为用户提供了很多优秀的解决方案。 MySQL 是一…...

刷题记录:牛客NC24261[USACO 2019 Feb G]Cow Land
传送门:牛客 题目描述 Cow Land 总共有 NNN 个不同的景点( 2≤N≤1052 \leq N \leq 10^52≤N≤105 )。 一共有 n−1n-1n−1 条道路连接任意两个景点,这意味着任意两个景点间只有一条简单路径。 每个景点 iii 都有一个享受值 eie_iei &…...

MYSQL开发误区
一、表、列、索引设计误区 1、现象:在线业务系统出现了三张表以上的关联查询 建议:说明业务逻辑在表设计上的实现不合理,需要进行表结构调整,或进行列的冗余,或进行业务改造。 2、现象:大表拆成多张小表之…...
k8s学习之路 | k8s 工作负载 DaemonSet
文章目录1. DaemonSet 基础1.1 什么是 DS1.2 DS 的典型用法1.3 如何编写 DS 资源1.4 DS 示例文件1.5 DS Pod 是如何被调度的1.6 更新 DS1.7 DS 替代方案1.8 DS 工作负载字段描述2. DaemonSet 的使用2.1 每个节点运行一个2.2 DS 更新策略2.3 滚动更新2.4 OnDelete 更新2.6 更新回…...
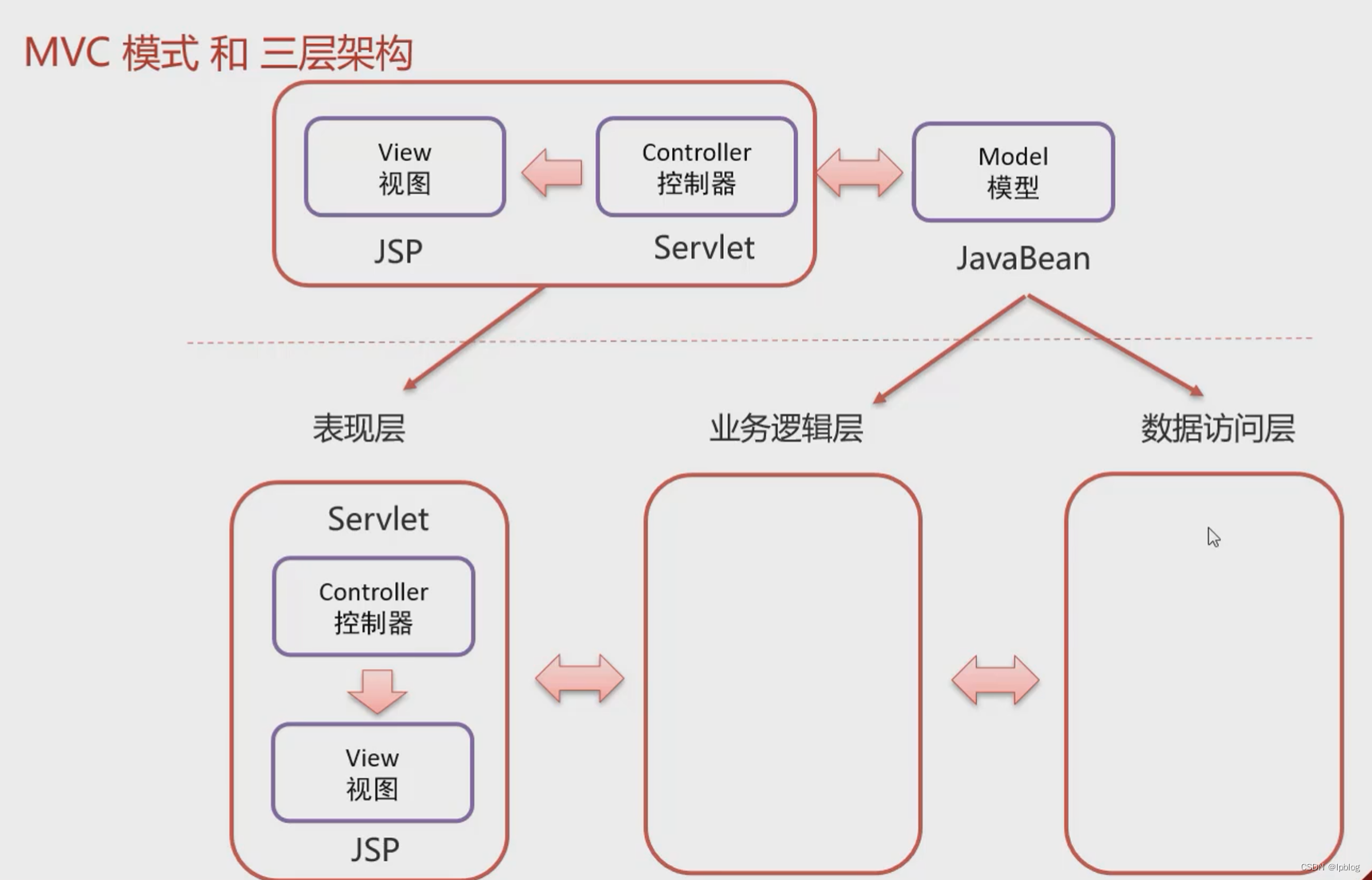
Javaweb MVC模式和三层架构
MVC 模式和三层架构是一些理论的知识,将来我们使用了它们进行代码开发会让我们代码维护性和扩展性更好。 7.1 MVC模式 MVC 是一种分层开发的模式,其中: M:Model,业务模型,处理业务 V:View&am…...

综合考虑,在客户端程序中嵌入网页程序,首选CefSharp。
综合考虑,在客户端程序中嵌入网页程序,首选CefSharp。 CefSharp 是一种将全功能符合标准的 Web 浏览器嵌入 C# 或 VB.NET 应用程序的简单方法。 https://www.jianshu.com/p/3f50cc747606 WinForm嵌入Web网页的解决方案 Microsoft Edge WebView2诞生较晚…...

【Java基础 下】 030 -- 网络编程
目录 一、什么是网络编程 1、常见的软件架构(CS & BS) ①、BS架构的优缺点 ②、CS架构的优缺点 2、小结 二、网络编程三要素 1、IP ①、IPv4 ②、IPv6 ③、小结 ④、IPv4的一些细节 ⑤、InetAddress的使用 2、端口号 3、协议 ①、TCP & UDP 三、…...
 T3打拳)
2021牛客OI赛前集训营-提高组(第三场) T3打拳
2021牛客OI赛前集训营-提高组(第三场) 题目大意 有2n2^n2n个选手参加拳击比赛,每个人都有一个实力,所有选手的实力用一个111到2n2^n2n的排列表示。 淘汰赛的规则是:每次相邻的两个选手进行比赛,实力值大…...

C++面向对象编程之四:成员变量和成员函数分开存储、this指针、const修饰成员和对象
在C中,成员变量和成员函数是分开存储的,只有非静态成员变量才存储在类中或类的对象上。通过该类创建的所有对象都共享同一个函数#include <iostream> using namespace std;class Monster {public://成员函数不占对象空间,所有对象共享同…...
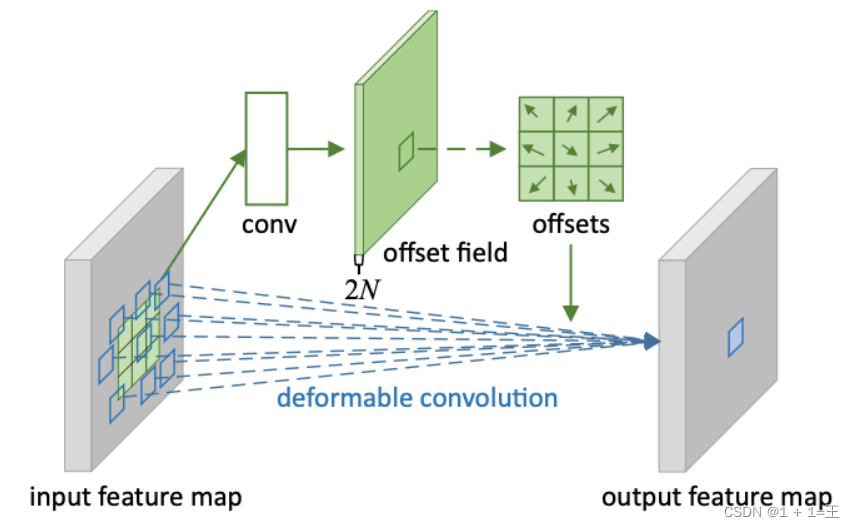
卷积神经网络(CNN)基础知识
文章目录CNN的组成层卷积层卷积运算卷积的变种分组卷积转置卷积空洞卷积可变形卷积卷积层的输出尺寸和参数量CNN的组成层 在卷积神经⽹络中,⼀般包含5种类型的⽹络层次结构:输入层、卷积层、激活层、池化层和输出层。 输入层(input layer&a…...

opencv+python 常见图像预处理
import os import cv2 import numpy as np import pandas as pd from PIL import Image import matplotlib.pylab as plt """图像预处理"""#缩放 #灰度化 #二值化-otsu,自定义,自适应 #均值滤波 #中值滤波 #自定义滤波 #高斯/双倍滤波…...

如何实现一个单例模式
目录 前言 1.饿汉式 2.懒汉式 3.双重检测 4.静态内部类 5.枚举 总结: 前言 单例模式是我们日常开发过程中,遇到的最多的一种设计模式。通过这篇文章主要分享是实现单例的几种实现方式。 1.饿汉式 饿汉式的实现方式比较简单。在类加载的时候&#…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...
