【LeetCode热题100总结】239. 滑动窗口最大值
题目描述
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
示例 1:
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3
输出:[3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
示例 2:
输入:nums = [1], k = 1
输出:[1]
提示:
1 <= nums.length <= 10^5
-104 <= nums[i] <= 10^4
1 <= k <= nums.length
以下参考力扣官方题解:
链接:https://leetcode.cn/problems/sliding-window-maximum/solutions/543426/hua-dong-chuang-kou-zui-da-zhi-by-leetco-ki6m/
相关标签
队列、滑动窗口、单调队列、堆(优先队列)
解题思路
对于每个滑动窗口,可以使用 O ( k ) O(k) O(k)的时间遍历每个元素,找到最大值。对于长度为 n 的数组 nums,窗口的数量为 n-k+1,因此算法的时间复杂度为 O ( ( n − k + 1 ) k ) = O ( n k ) O((n-k+1)k)=O(nk) O((n−k+1)k)=O(nk),会超出时间限制,需要进行一些优化。可以想到,对于两个相邻(只差一个位置)的滑动窗口,共用着 k-1 个元素,只有一个元素是变化的,可以根据这个特点进行优化。
解法1:优先队列
对于最大值,可以想到一种非常合适的数据结构,优先队列(堆),其中的大根堆可以帮助我们实时维护一系列元素中的最大值。
初始时,将数组的前k个元素放入优先队列中。每当向右移动窗口时,可以把一个新的元素放入优先队列中,此时堆顶的元素就是堆中所有元素的最大值。然而这个最大值可能不在滑动窗口中,而是出现在滑动窗口左边界的左侧。因此当我们继续向右移动窗口时这个值就永远不可能出现在滑动窗口中了,我们可以将其从优先队列中删除。
我们不断地移除堆顶元素,直到其确实出现在滑动窗口中。此时,堆顶元素就是滑动窗口中的最大值。为了方便判断堆顶元素和滑动窗口的位置关系,我们可以在有限队列中存储二元组 ( n u m , i n d e x ) (num, index) (num,index),表示元素 num 在数组中的下标为 index。
code
class Solution:def maxSlidingWindow(self, nums:List[int], k:int) -> List[int]:n = len(nums)# python 默认的优先队列是小根堆q = [(-nums[i], i) for i in range(k)]heapq.heapify(q) ans = [-q[0][0]]for i in range(k, n):heapq.heappush(q, (-nums[i], i))while q[0][1] <= i-k:heapq.heappop(q)ans.append(-q[0][0])return ans
Python的heapq库是用于实现堆(优先队列)算法的库。它提供了一些函数来操作堆结构,如push、pop、heapify等。
heapq.heapify(q):将列表heap原地转换为一个堆。
heapq.heappush(heap, item:将元素item推入堆heap上。
heapq.heappop(q):从堆heap中弹出并返回最小的元素。
复杂度分析:
- 时间复杂度: O ( n l o g n ) O(nlogn) O(nlogn),其中n数数组 nums 的长度。在最坏情况下数组的元素单调递增,那么最终优先队列中包含了所有元素,没有元素被移除。由于将一个元素放入优先队列的时间复杂度为 O ( n ) O(n) O(n),因此总时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn)。
- 空间复杂度: O ( n ) O(n) O(n),即优先队列需要使用的空间。这里所有的空间复杂度分析都不考虑返回的答案需要的空间,只计算额外的空间使用。
解法2:单调队列
由于我们需要求出的是滑动窗口的最大值,如果当前的滑动窗口中有两个下标i 和j,其中i 在 j的坐标,并且i 对应的元素不大于 j 对应的元素。那么当滑动窗口向右移动时,只要i 还在窗口中,那么j 一定也还在窗口中。因此i对应的元素一定不会是窗口中的最大值了,可以将其永久移除。
因此可以使用一个队列存储所有还没有被移除的下标,在队列中这些下标按照从小到大的顺序被存储,并且在数组nums中对应的值是严格单调递减的。
当窗口向右移动时,为了保持队列的性质,会不断将新的元素和队尾的元素相比较,如果前者大于等于后者,那么队尾的元素就可以被永久移除,弹出队列。不断进行此操作,知道队列为空或新元素小于队尾元素。
由于队列中下标对应的元素是严格单减的,因此队首下标对应的元素就是滑动窗口中的最大值。此时最大值可能在窗口左边界的左侧,因此还需要不断从队首弹出元素,直到队首元素在窗口中。
为了科研同时弹出队首和队尾的元素,需要使用双端队列。满足这种单调性的双端队列一般称为单调队列。
class Solution:def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:n = len(nums)q = collections.deque()for i in range(k):while q and nums[i] >= nums[q[-1]]:q.pop()q.append(i)ans = [nums[q[0]]]for i in range(k, n):while q and nums[i] >= nums[q[-1]]:q.pop()q.append(i)while q[0] <= i - k:q.popleft()ans.append(nums[q[0]])return ans
复杂度分析
- 时间复杂度: O ( n ) O(n) O(n)。每个下标恰好被放入队列一次,并且最多被弹出队列一次。
- 空间复杂度:这里使用的数据结构是双向的,因此不断从队首弹出元素保证了队列中最多不会有超过 k+1 个元素,因此队列使用的空间为 O ( k ) O(k) O(k)。
解法3: 分块 + 预处理
可以将数组nums从左到右按照k个一组进行分组,最后一组中元素的数量可能会不足k个。如果希望求出nums[i]到nums[i+k-1]的最大值就会有两种情况:
- 如果 i 是 k 的倍数,那么 nums[i] 到 nums[i+k-1] 恰好是一个分组。只要预处理出每个分组中的最大值即可;
- 如果 i 不是 k 的备注,那么会跨越两个分组,占有第一个分组的后缀以及第二个分组的前缀。假设 j 是 k 的倍数,并且 i < j <= j+k-1,那么 nums[i]~nums[j-1]就是第一个分组的后缀,nums[j] 到 nums[i+k-1] 就是第二个分组的前缀。如果预处理出每个分组中的前缀最大值和后缀最大值,也可以在 O(1) 的时间得到答案。
用 prefixMax [ I ] \textit{prefixMax}[I] prefixMax[I]表示下标 i 对应的分组中,以 i 结尾的前缀最大值; suffixMax [ i ] \textit{suffixMax}[i] suffixMax[i] 表示下标 i 对应的分组中,以 i 开始的后缀最大值。它们分别满足如下的递推式
prefixMax [ i ] = { nums [ i ] , i 是 k 的倍数 max { prefixMax [ i − 1 ] , nums [ i ] } , i 不是 k 的倍数 \textit{prefixMax}[i]=\begin{cases} \textit{nums}[i], & \quad i ~是~ k ~的倍数 \\ \max\{ \textit{prefixMax}[i-1], \textit{nums}[i] \}, & \quad i ~不是~ k ~的倍数 \end{cases} prefixMax[i]={nums[i],max{prefixMax[i−1],nums[i]},i 是 k 的倍数i 不是 k 的倍数
以及
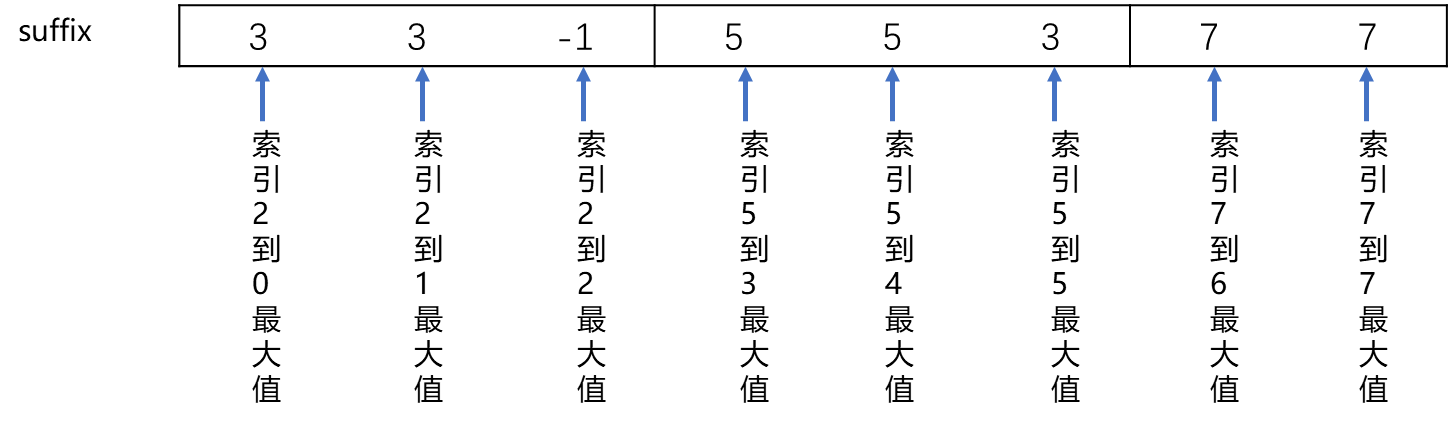
suffixMax [ i ] = { nums [ i ] , i + 1 是 k 的倍数 max { suffixMax [ i + 1 ] , nums [ i ] } , i + 1 不是 k 的倍数 \textit{suffixMax}[i]=\begin{cases} \textit{nums}[i], & \quad i+1 ~是~ k ~的倍数 \\ \max\{ \textit{suffixMax}[i+1], \textit{nums}[i] \}, & \quad i+1 ~不是~ k ~的倍数 \end{cases} suffixMax[i]={nums[i],max{suffixMax[i+1],nums[i]},i+1 是 k 的倍数i+1 不是 k 的倍数
需要注意在递推 suffixMax [ i ] \textit{suffixMax}[i] suffixMax[i] 时需要考虑到边界条件 suffixMax [ n − 1 ] = nums [ n − 1 ] \textit{suffixMax}[n-1]=\textit{nums}[n-1] suffixMax[n−1]=nums[n−1],而在递推 prefixMax [ I ] \textit{prefixMax}[I] prefixMax[I] 时的边界条件 prefixMax [ 0 ] = nums [ 0 ] \textit{prefixMax}[0]=\textit{nums}[0] prefixMax[0]=nums[0] 恰好包含在递推式的第一种情况中,因此无需特殊考虑。
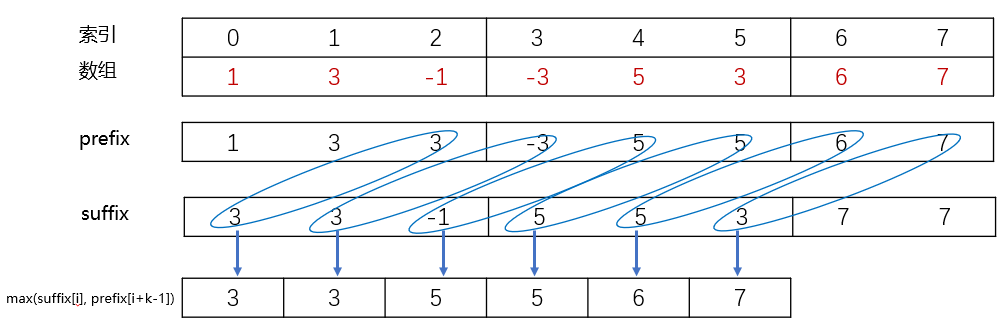
在预处理完成之后,对于 nums [ I ] \textit{nums}[I] nums[I]到 nums [ i + k − 1 ] \textit{nums}[i+k-1] nums[i+k−1] 的所有元素,如果 i 不是 k 的倍数,那么窗口中的最大值为 suffixMax [ I ] \textit{suffixMax}[I] suffixMax[I] 与 prefixMax [ i + k − 1 ] \textit{prefixMax}[i+k-1] prefixMax[i+k−1] 中的较大值;如果 i 是 k 的倍数,那么此时窗口恰好对应一整个分组, suffixMax [ I ] \textit{suffixMax}[I] suffixMax[I] 和 prefixMax [ i + k − 1 ] \textit{prefixMax}[i+k-1] prefixMax[i+k−1] 都等于分组中的最大值,因此无论窗口属于哪一种情况,
suffixMax [ i ] , prefixMax [ i + k − 1 ] } \textit{suffixMax}[i], \textit{prefixMax}[i+k-1] \big\} suffixMax[i],prefixMax[i+k−1]}即为答案。
此方法和稀疏表(Sparse Table)很类似。
class Solution:def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:n = len(nums)prefixMax, suffixMax = [0] * n, [0] * nfor i in range(n):if i % k == 0:prefixMax[i] = nums[i]else:prefixMax[i] = max(prefixMax[i - 1], nums[i])for i in range(n - 1, -1, -1):if i == n - 1 or (i + 1) % k == 0:suffixMax[i] = nums[i]else:suffixMax[i] = max(suffixMax[i + 1], nums[i])ans = [max(suffixMax[i], prefixMax[i + k - 1]) for i in range(n - k + 1)]return ans
复杂度分析
- 时间复杂度:O(n);
- 空间复杂度:存储prefixMax和suffixMax需要的空间。
评论区一个很好的示例:

相关文章:

【LeetCode热题100总结】239. 滑动窗口最大值
题目描述 给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。 返回 滑动窗口中的最大值 。 示例 1: 输入:nums [1,3,-1,-3,5,3,6,7]…...

【YOLOv9改进[Conv]】使用YOLOv10的空间通道解耦下采样SCDown模块替换部分CONv的实践 + 含全部代码和详细修改内容
本文将使用YOLOv10的空间通道解耦下采样SCDown模块替换部分CONv的实践 ,文中含全部代码和详细修改内容。 目录 一 YOLOv10 1 空间通道解耦下采样 2 可视化...

简单小游戏制作
控制台基础设置 //隐藏光标 Console.CursorVisible false; //通过两个变量来存储舞台的大小 int w 50; int h 30; //设置舞台(控制台)的大小 Console.SetWindowSize(w, h); Console.SetBufferSize(w, h);多个场景 int nowSceneID 1; while (true) …...

Delphi
Delphi,是美国 Borland(宝兰)公司於 1995 年开发在 Windows 平台下的快速应用程式开发工具 (Rapid Application Development,简称 RAD),它的前身是在 DOS 下的产品 Borland Turbo Pascal。(非开源软件&…...

Linux的shell脚本中的比大小
如果要将 -le 换成相反的(即“大于”),你应该使用 -gt(greater than)。 所以,-le 的相反比较是 -gt。 但如果你想要一个包含“大于”和“不等于”的比较(即“大于”),那…...

每日复盘-20240603
20240603 六日涨幅最大: ------1--------300637--------- 扬帆新材 五日涨幅最大: ------1--------300637--------- 扬帆新材 四日涨幅最大: ------1--------301306--------- 西测测试 三日涨幅最大: ------1--------301306--------- 西测测试 二日涨幅最大: ------1--------30…...
 doesn‘t match this client (41); killing...)
adb server version (22000) doesn‘t match this client (41); killing...
参考链接: adb server version (31) doesn’t match this client (41); killing… 解决此问题 电脑安装了360手机助手占用了adb的端口引起的。因为套接字的唯一性(一个套接字只能由 协议/网络地址/端口号 唯一确定 ),一个电脑只能有一个程序…...
如何使用 Connector API 将数据提取到 Elasticsearch Serverless 中
作者:来自 Elastic Jedr Blaszyk Elasticsearch 支持一系列摄取方法。 其中之一是 Elastic Connectors,它将 SQL 数据库或 SharePoint Online 等外部数据源与 Elasticsearch 索引同步。 连接器对于在现有数据之上构建强大的搜索体验特别有用。 例如&…...

体育赛事直播系统开发源码搭建
随着体育产业的蓬勃发展,体育赛事直播已成为广大观众获取赛事信息的重要途径。为了满足观众日益增长的需求,开发一套专业的体育赛事直播系统成为当务之急。本文将围绕体育赛事直播系统开发源码搭建进行深入探讨,从技术选型、系统架构、安全防…...

使用Jmeter进行性能测试
学习视频 B站UP主:白月黑羽编程 目录 Jmeter的下载 Jmeter界面 Jmeter操作 线程组与HTTP请求 测试一个请求 解决响应数据中 中文乱码的问题 HTTP请求默认值 录制网站流量 添加录制控制器 添加HTTP代理服务器 在浏览器配置代理 进行录制 模拟间隔时间 …...

AI技术的发展,会让你工作轻松吗
这两年,人工智能技术迅猛发展,AI产品层出不穷,尤其大语言模型(LLM)的爆火,许多人担心自己的工作会被AI取代。然而,如果AI技术发展到极致,再加上其他科学技术的高度发展,我…...
Spring-DI入门案例
黑马程序员SSM框架教程 文章目录 一、DI入门案例思路分析二、实现步骤2.1 删除service中使用new形式创建的Dao对象2.2 提供以来对象对应的setter方法2.3 配置service与到之间的关系 一、DI入门案例思路分析 基于IoC管理bean(上个案例已经实现)service中…...

ubuntu18.04 报错:fatal error: execution
一、问题描述 在ubuntu18.04上编译Faster-lio 报错: fatal error: execution: 没有那个文件或目录#include <execution> 二、解决方法 需要将g编译器更新到9.0 sudo add-apt-repository ppa:ubuntu-toolchain-r/test sudo apt update sudo apt install g…...

开源大模型与大模型api的使用优缺点
开源大模型和大模型 API 都是人工智能领域中的重要概念,它们各自有一些优缺点。 开源大模型: 优点: 免费使用: 大多数开源大模型是免费提供的,任何人都可以访问和使用这些模型,降低了使用门槛。可定制性…...

小红书前端2轮面试期望22K,全程问低代码设计
一面(通过) 1、好,那我们开始把,先简单介绍一下自己的一个经历,以及自己有亮点的项目?balabala 2、你可以这样介绍:在这里边主要负责哪几个项目,哪些项目是比较有亮点的࿰…...
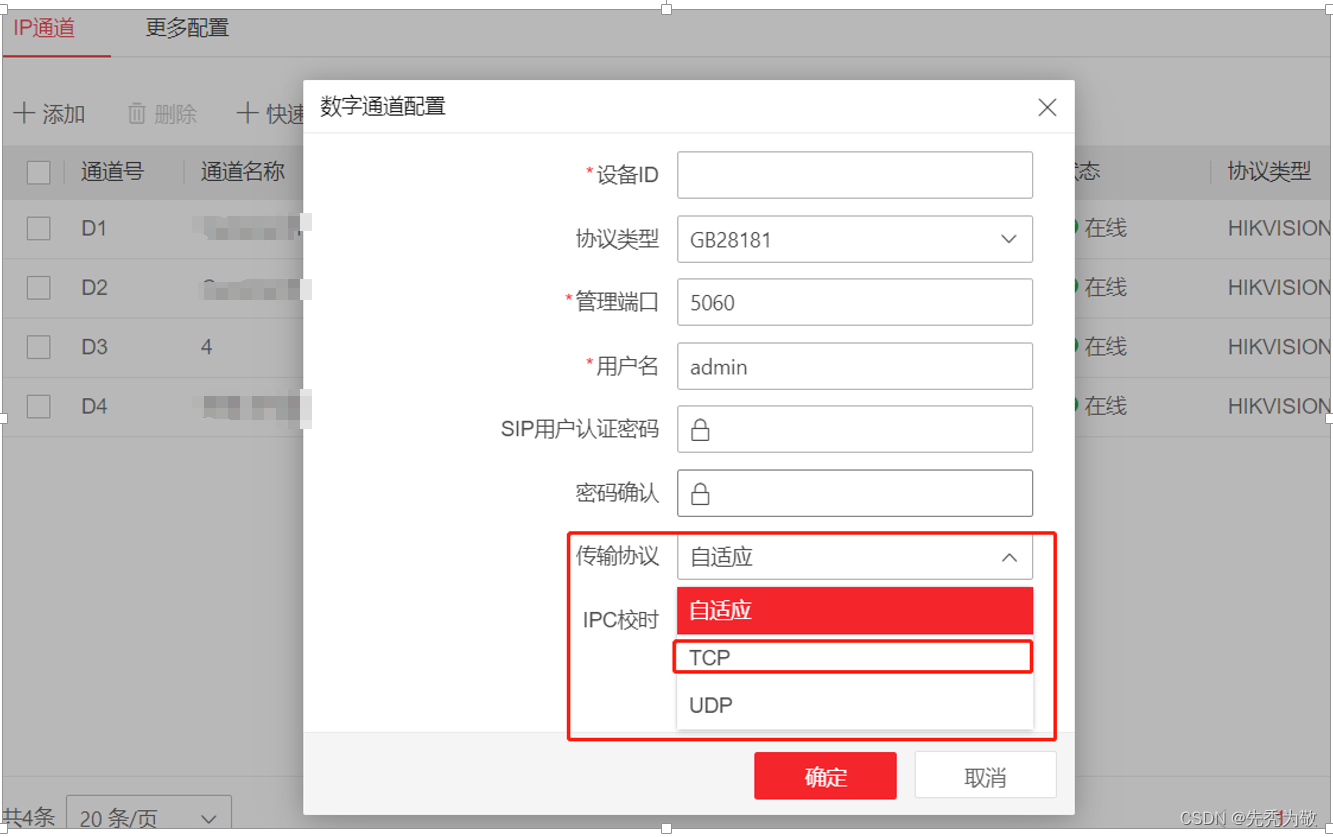
HIK录像机GB28181对接相机不在线问题随笔
一、问题现象 【设备信息】型号:DS-8664N-I16-V3 V4.63.000 build 230412 【问题现象】HIK录像机使用GB28181对接异常相机无法正常上线,对接HIK相机可以正常上线。 【现场拓扑】现场拓扑如下 NVR侧使用固定公网IP地址。IPC侧使用家用宽带的方式&…...
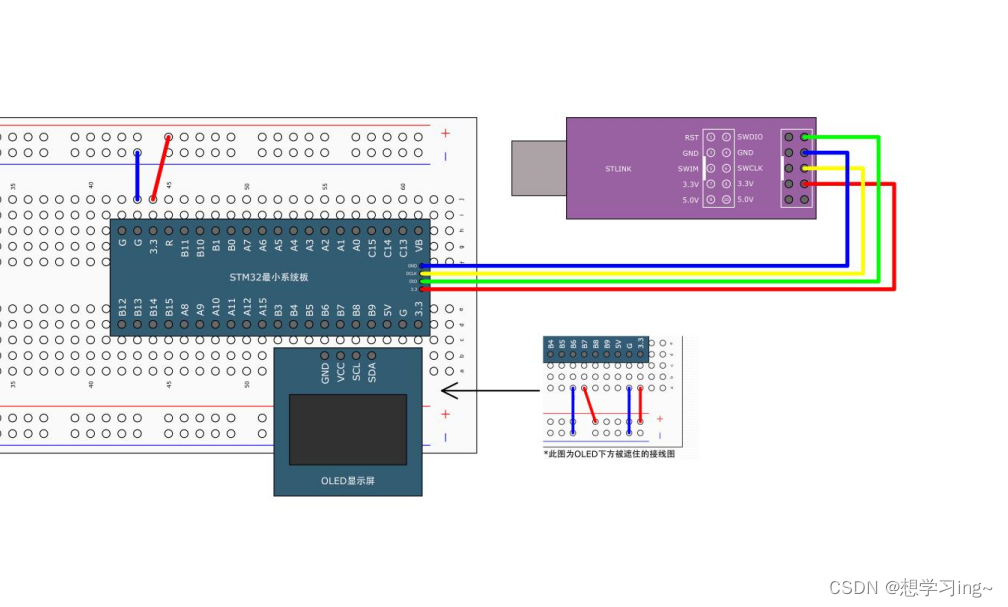
stm32-DMA转运数据
在配置前要记得先定义一下DMA转运的源端数组和目标数组两个数组哦。 接下来我们就开始准备配置吧 配置 初始化 1.RCC开启时钟(开启DMA的时钟) void RCC_AHBPeriphClockCmd(uint32_t RCC_AHBPeriph, FunctionalState NewState) 作用:开启时…...

Java编程常见问题汇总一
系列文章目录 文章目录 系列文章目录前言一、字符串连接误用二、错误的使用StringBuffer三、测试字符串相等性四、数字转换成字符串五、利用不可变对象(Immutable) 前言 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分…...
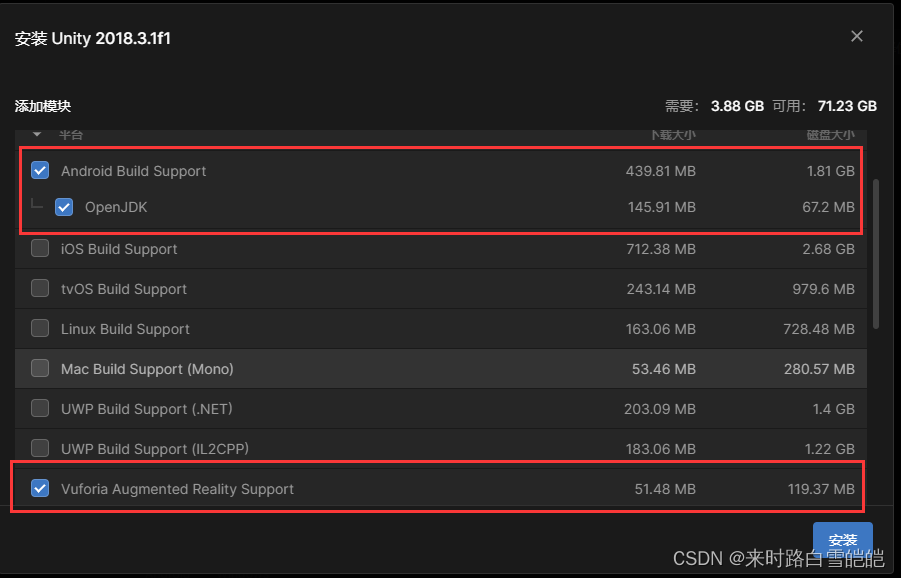
用Unityhub安装unity2018.3.0和vuforia
打开下载网址 https://unity.cn/releases/full/2018 选择2018.3.x 找到2018.3.0后,点击从UnityHub下载 然后unityhub会弹出安装界面 只勾选这两个,其余的全部取消勾选,默认勾选上的也取消掉,然后点击安装...

智汇云舟与芯瞳完成兼容适配,共建国产化生态体系
近日,智汇云舟的视频孪生系列产品和时空大数据系列产品已完成与芯瞳半导体技术(山东)有限公司GPU产品GB2062/GB2064/CQ2040/CQ2040 MXM/CQ2040 MD的相互兼容性测试认证。双方产品经过严格测试,已完成兼容适配,具备良好…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...
