卡方分布和 Zipf 分布模拟及 Seaborn 可视化教程
卡方分布
简介
卡方分布是一种连续概率分布,常用于统计学中进行假设检验。它描述了在独立抽样中,每个样本的平方偏差之和的分布。卡方分布的形状由其自由度 (df) 参数决定,自由度越大,分布越平缓。
参数
卡方分布用两个参数来定义:
df:自由度,表示卡方分布的形状。自由度必须为正整数。
size:输出数组的形状。
公式
卡方分布的概率密度函数 (PDF) 为:
f(x) = (x^(df/2 - 1) * np.exp(-x/2)) / (2^(df/2) * Gamma(df/2)) for x >= 0
其中:
f(x):表示在 x 点的概率密度。
x:非负实数。
df:自由度。
np.exp(-x/2):指数函数。
Gamma(df/2):伽马函数。
生成卡方分布数据
NumPy 提供了 random.chisquare() 函数来生成服从卡方分布的随机数。该函数接受以下参数:
df:自由度。
size:输出数组的形状。
示例:生成 10 个自由度为 5 的卡方分布随机数:
import numpy as npdata = np.random.chisquare(df=5, size=10)
print(data)
可视化卡方分布
Seaborn 库提供了便捷的函数来可视化分布,包括卡方分布。
示例:绘制 1000 个自由度为 5 的卡方分布随机数的分布图:
import seaborn as sns
import numpy as npdata = np.random.chisquare(df=5, size=1000)
sns.distplot(data)
plt.show()
练习
- 模拟 20 个自由度为 10 的卡方分布随机数,并绘制它们的分布图。
- 比较不同自由度下卡方分布形状的变化。
- 利用卡方分布来进行卡方检验,假设某枚硬币是公平的,即正面朝上的概率为 0.5。抛掷硬币 100 次,并计算正面朝上的次数是否服从二项分布。
解决方案
import seaborn as sns
import numpy as np
from scipy import stats# 1. 模拟随机数并绘制分布图
data = np.random.chisquare(df=10, size=20)
sns.distplot(data)
plt.show()# 2. 比较不同自由度下分布形状的变化
df_values = [2, 5, 10, 20]
for df in df_values:data = np.random.chisquare(df=df, size=1000)sns.distplot(data, label=f"df={df}")
plt.legend()
plt.show()# 3. 进行卡方检验
heads = np.random.binomial(n=100, p=0.5)
chi2_stat, p_value = stats.chisquare(heads, f_exp=50)
print("卡方统计量:", chi2_stat)
print("p 值:", p_value)# 由于 p 值大于 0.05,无法拒绝原假设,即可以认为硬币是公平的。
瑞利分布
简介
瑞利分布是一种连续概率分布,常用于描述信号处理和雷达系统中的幅度分布。它表示在一个随机变量的平方根服从指数分布时,该随机变量的分布。
参数
瑞利分布用一个参数来定义:
scale:尺度参数,控制分布的平坦程度。较大的尺度参数使分布更加平坦,两侧尾部更加分散。默认为 1。
公式
瑞利分布的概率密度函数 (PDF) 为:
f(x) = (x scale) / (scale^2 np.exp(-x^2 / (2 scale^2))) for x >= 0
其中:
f(x):表示在 x 点的概率密度。
x:非负实数。
scale:尺
Zipf分布
简介
Zipf分布,又称为Zeta分布,是一种离散概率分布,常用于描述自然语言、人口统计学、城市规模等领域中具有幂律特征的数据分布。它体现了“少数服从多数”的现象,即排名越靠前的元素出现的频率越高。
参数
Zipf分布用一个参数来定义:
a:分布参数,控制分布的形状。a越小,分布越偏向于少数元素,越接近幂律分布。默认为 2。
公式
Zipf分布的概率质量函数 (PMF) 为:
P(k) = 1 / (k ^ a) for k >= 1
其中:
P(k):表示第 k 个元素出现的概率。
k:元素的排名,从 1 开始。
a:分布参数。
生成Zipf分布数据
NumPy提供了random.zipf()函数来生成服从Zipf分布的随机数。该函数接受以下参数:
a:分布参数。
size:输出数组的形状。
示例:生成10个服从Zipf分布的随机数,分布参数为2:
import numpy as npdata = np.random.zipf(a=2, size=10)
print(data)
可视化Zipf分布
Seaborn库提供了便捷的函数来可视化分布,包括Zipf分布。
示例:绘制1000个服从Zipf分布的随机数的分布图,分布参数为2:
import seaborn as sns
import numpy as npdata = np.random.zipf(a=2, size=1000)
sns.distplot(data)
plt.show()
练习
- 模拟不同分布参数下Zipf分布形状的变化。
- 利用Zipf分布来模拟一个城市的规模分布,并计算排名前10的城市人口占总人口的比例。
- 比较Zipf分布与幂律分布的异同。
解决方案
import seaborn as sns
import numpy as np# 1. 模拟不同分布参数下Zipf分布形状的变化
a_values = [1.5, 2, 2.5, 3]
for a in a_values:data = np.random.zipf(a=a, size=1000)sns.distplot(data, label=f"a={a}")
plt.legend()
plt.show()
2. 模拟城市规模分布并计算人口比例
population = np.random.zipf(a=2, size=100)
top10_population = population[:10].sum()
total_population = population.sum()
print(“排名前10的城市人口:”, top10_population)
print(“排名前10的城市人口比例:”, top10_population / total_population)
3. Zipf分布与幂律分布的比较
Zipf分布和幂律分布都描述了“少数服从多数”的现象,即排名越靠前的元素出现的频率越高。
但是,Zipf分布的参数化程度更高,可以更精确地描述不同领域的幂律现象。幂律分布则更通用,但缺乏Zipf分布对参数的控制能力。
具体来说,Zipf分布的PMF为:
P(k) = 1 / (k ^ a)
幂律分布的PMF为:
P(k) = C / k ^ alpha
其中,C为归一化常数。
可见,Zipf分布的参数a控制了分布的倾斜程度,而幂律分布的参数alpha则控制了分布的整体形状。
此外,Zipf分布通常用于描述离散数据,而幂律分布则可以用于描述离散和连续数据。
最后
为了方便其他设备和平台的小伙伴观看往期文章:
微信公众号搜索:Let us Coding,关注后即可获取最新文章推送
看完如果觉得有帮助,欢迎点赞、收藏、关注
相关文章:

卡方分布和 Zipf 分布模拟及 Seaborn 可视化教程
卡方分布 简介 卡方分布是一种连续概率分布,常用于统计学中进行假设检验。它描述了在独立抽样中,每个样本的平方偏差之和的分布。卡方分布的形状由其自由度 (df) 参数决定,自由度越大,分布越平缓。 参数 卡方分布用两个参数来…...

音视频开发13 FFmpeg 音频 相关格式分析 -- AAC ADTS格式分析
这一节,我们学习常用的音频的格式 AAC,重点是掌握 AAC的传输格式 ADTS 头部的信息,目的是 : 当音频数据有问题的时候,如果是AAC的编码,在分析 头部信息的时候能够根据头部信息 判断问题是否出现在 头部。 A…...
周三晚19:00 | 数据资源入表案例拆解,他们如何应对入表难点?
数据资源入表的具体场景是怎样的?如何应对数据资源入表难点? 6月5日,即周三晚19:00,讲师-星光数智首席数据架构师 魏战松将继续带来关于《数据要素资产运营》的主题直播,为大家拆解数据资源入表的具体案例。 累计77…...

树的知识总结
一:树的基本术语(只写了查漏的部分 1 双亲:就是父节点 2 层序编号 3 有序无序树 4 森林 二:逻辑结构上与线性结构的比较 三:树的存储结构 ①双亲表示节点法:...

工业安全智勇较量,赛宁网安工业靶场决胜工业网络攻防对抗新战场
2024年1月30日,工信部发布《工业控制系统网络安全防护指南》(工信部网安〔2024〕14号),围绕安全管理、技术防护、安全运营、责任落实四方面提出安全防护要求,强调聚焦安全薄弱关键环节,强化技术应对策略&am…...
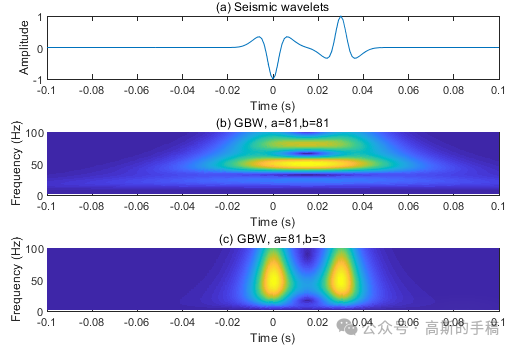
一种一维时间序列信号的广义小波变换方法(MATLAB)
地震波在含油气介质中传播时,其高频分量往往比低频分量衰减更快。据此,地震波的高频分量和低频分量之间的差异值可以用于分析含油气衰减位置,从而间接指示出含油气储层。对于时频域中的地震波衰减分析,一般地,利用地震…...

【GIC400】——驱动代码实现
文章目录 驱动代码实现IRQ 中断处理GIC 驱动GIC 使用使用示例系列文章 【ARMv7-A】——异常与中断 【ARMv7-A】——异常中断处理概述 【ARMv7-A】——进入和退出异常中断的过程 【GIC400】——PLIC,NVIC 和 GIC 中断对比 【GIC400】——GIC 简介 【GIC400】——GIC 相关的 CP1…...

如何在 Vue 组件中正确地使用 data 函数?
在 Vue 组件中正确使用 data 函数有以下几点需要注意: 返回一个对象: data 函数必须返回一个对象,这个对象包含了组件实例需要用到的所有数据属性。export default {data() {return {message: Hello, Vue!,count: 0}} }不要使用箭头函数: data 函数不应该使用箭头函数 () >…...

.Net 基于MiniExcel的导入功能接口示例
/// <summary>/// 导入/// </summary>/// <param name"formFile"></param>/// <returns></returns>[HttpPost("Import")]public async Task<ExecResult> Import(IFormFile formFile){try{if (formFile null) t…...

流量焦虑?别担心,Xinstall一站式App推广解决方案来了!
在移动互联网时代,App已经成为人们日常生活中不可或缺的一部分。然而,对于众多开发者来说,如何有效地推广自己的App,吸引更多的用户,却是一个不小的挑战。今天,我们将为大家介绍一款强大的App推广工具——X…...

降薪潮要开始了么?
互联网要全面迎来降薪潮了么,最近这个观念一直冲击着我 起因就是,前一段一位朋友降薪40%拿到了offer;还有一位金融机构的人力资源负责人朋友告诉我,最近来的很多互联网人都是降薪来的,普遍降30-50%不等 我就在想&…...

网络服务DHCP的安装
DHCP的安装 检查并且安装dhcp有关软件包 rpm -qc dhcp #检查是否存在dhcp yum install -y dhcp #进行yum安装查看系统的配置文件 切换到对应目录查看相关文件配置,发现是空目录。 将官方提供的example复制到原配置文件中 cp /usr/share/doc/dhcp-4.2.5/dhcpd.…...

SELinux:安全增强型Linux
SELinux:安全增强型Linux 作用: 可以保护linux系统的安全为用户分配最小的权限 状态: Enforcing:强制保护Permissive:宽松状态Disabled:禁用 为了安全性考虑,希望SELinux设置为Enforcing状态…...

.NET Redis限制接口请求频率 滑动窗口算法
在.NET中使用Redis来限制接口请求频率(每10秒只允许请求一次) NuGet setup StackExchange.Redis 实现速率限制逻辑: 在控制器或服务层中,编写Redis速率限制计数器。 设置Redis键: 为每个用户或每个IP地址设置一个唯一…...

Java List数据结构与常用方法
1.1 数据结构概述 Java的集合框架其实就是对数据结构的封装,在学习集合框架之前,有必要先了解下数据结构。 1.1.1 什么是数据结构 所谓数据结构,其实就是计算机存储、组织数据的方式。 数据结构是用来分析研究数据存储操作的,其实…...
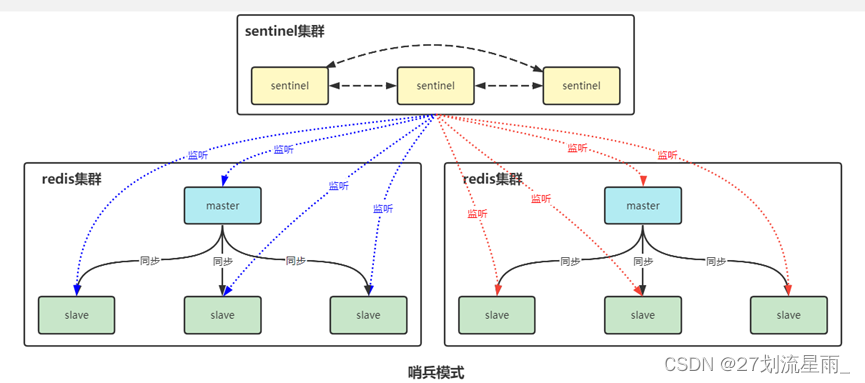
Docker搭建redis-cluster集群
1. 前期准备 1.1 拉redis镜像 docker search redis docker pull redis1. 2 创建网卡 docker network create myredis --subnet 172.28.0.0/16#查看创建的网卡 docker network inspect myredisdocker network rm myredis #删除网卡命令 多个中间 空格隔开 docker network --h…...

实验室类管理平台LIMS系统的ui设计实例
实验室类管理平台LIMS系统的ui设计实例...

<PLC><西门子><工控>西门子博图V18中使用SCL语言编写一个CRC16-modbus校验程序
前言 本系列是关于PLC相关的博文,包括PLC编程、PLC与上位机通讯、PLC与下位驱动、仪器仪表等通讯、PLC指令解析等相关内容。 PLC品牌包括但不限于西门子、三菱等国外品牌,汇川、信捷等国内品牌。 除了PLC为主要内容外,PLC相关元器件如触摸屏(HMI)、交换机等工控产品,如…...

Linux - 文件管理高级 find、grep
0.管道 | 将前面命令的标准输出传递给管道作为后面的标准输入 1.文件查找 find find 进行文件查找时,默认进行递归查找,会查找隐藏目录下的文件 1.1 用法 # find 查找路径 查找条件... -type // 文件类型 f 普通文件 b 设备 d …...

DOS编程入门:探索基础、深入技巧与实战应用
DOS编程入门:探索基础、深入技巧与实战应用 DOS编程,作为计算机编程的基石之一,对于初学者来说,既是一种挑战,也是一次深入了解计算机底层运作的绝佳机会。本文将从四个方面、五个方面、六个方面和七个方面࿰…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...
