对称二叉树[简单]
优质博文:IT-BLOG-CN

一、题目
给你一个二叉树的根节点root, 检查它是否轴对称。
示例 1:
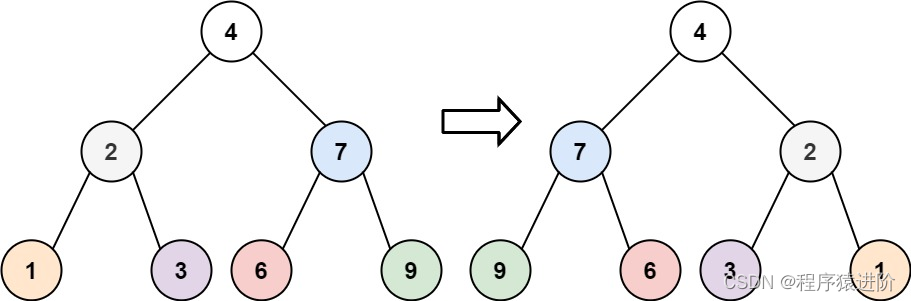
输入:root = [1,2,2,3,4,4,3]
输出:true
示例 2:
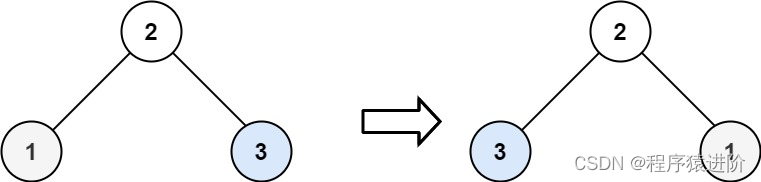
输入:root = [1,2,2,null,3,null,3]
输出:false
树中节点数目在范围
[1, 1000]内
-100 <= Node.val <= 100
进阶: 你可以运用递归和迭代两种方法解决这个问题吗?
二、代码
【1】递归: 我们将一个树的左右节点相同,转换为两个根节点具有相同的值,每个树的右子树都与另一个树的左子树镜像对称。我们通过一个递归函数,通过同步移动两个指针的方式来遍历树,rootLeft和rootRight都指向一个树的根,然后rootLeft右移时,rootRight左移,rootLeft左移时,rootRight右移。检查rootLeft和rootRight的值是否相等,如果相等再判断左右子树是否对称。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public boolean isSymmetric(TreeNode root) {return check(root, root);}private boolean check(TreeNode rootLeft, TreeNode rootRight) {if (rootLeft == null && rootRight == null) {return true;}if (rootLeft == null || rootRight == null) {return false;}return rootLeft.val == rootRight.val && check(rootLeft.left, rootRight.right) && check(rootLeft.right, rootRight.left);}
}
**时间复杂度:** 这里遍历了这棵树,渐进时间复杂度为`O(n)`。
**空间复杂度:** 这里的空间复杂度和递归使用的栈空间有关,这里递归层数不超过`n`,故渐进空间复杂度为`O(n)`。
【2】迭代: 我们引入一个队列,这是把递归程序改写成迭代程序的常用方法。初始化时我们把根节点入队两次。每次提取两个结点并比较它们的值(队列中每两个连续的结点应该是相等的,而且它们的子树互为镜像),然后将两个结点的左右子结点按相反的顺序插入队列中。当队列为空时,或者我们检测到树不对称(即从队列中取出两个不相等的连续结点)时,该算法结束。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public boolean isSymmetric(TreeNode root) {return check(root, root);}private boolean check(TreeNode rootLeft, TreeNode rootRight) {Queue<TreeNode> q = new LinkedList<TreeNode>();q.offer(rootLeft);q.offer(rootRight);while(!q.isEmpty()) {rootLeft = q.poll();rootRight = q.poll();if (rootLeft == null && rootRight == null) {continue;}if ((rootLeft == null || rootRight == null) || (rootLeft.val != rootRight.val)) {return false;}q.offer(rootLeft.left);q.offer(rootRight.right);q.offer(rootLeft.right);q.offer(rootRight.left);}return true;}
}
时间复杂度: 这里遍历了这棵树,渐进时间复杂度为O(n)。
空间复杂度: 这里需要用一个队列来维护节点,每个节点最多进队一次,出队一次,队列中最多不会超过n个点,故渐进空间复杂度为O(n)。
【3】对称二叉树定义: 对于树中 任意两个对称节点L和R,一定有:
L.val = R.val :即此两对称节点值相等。
L.left.val = R.right.val :即L的 左子节点 和R的 右子节点 对称。
L.right.val = R.left.val :即L的 右子节点 和R的 左子节点 对称。
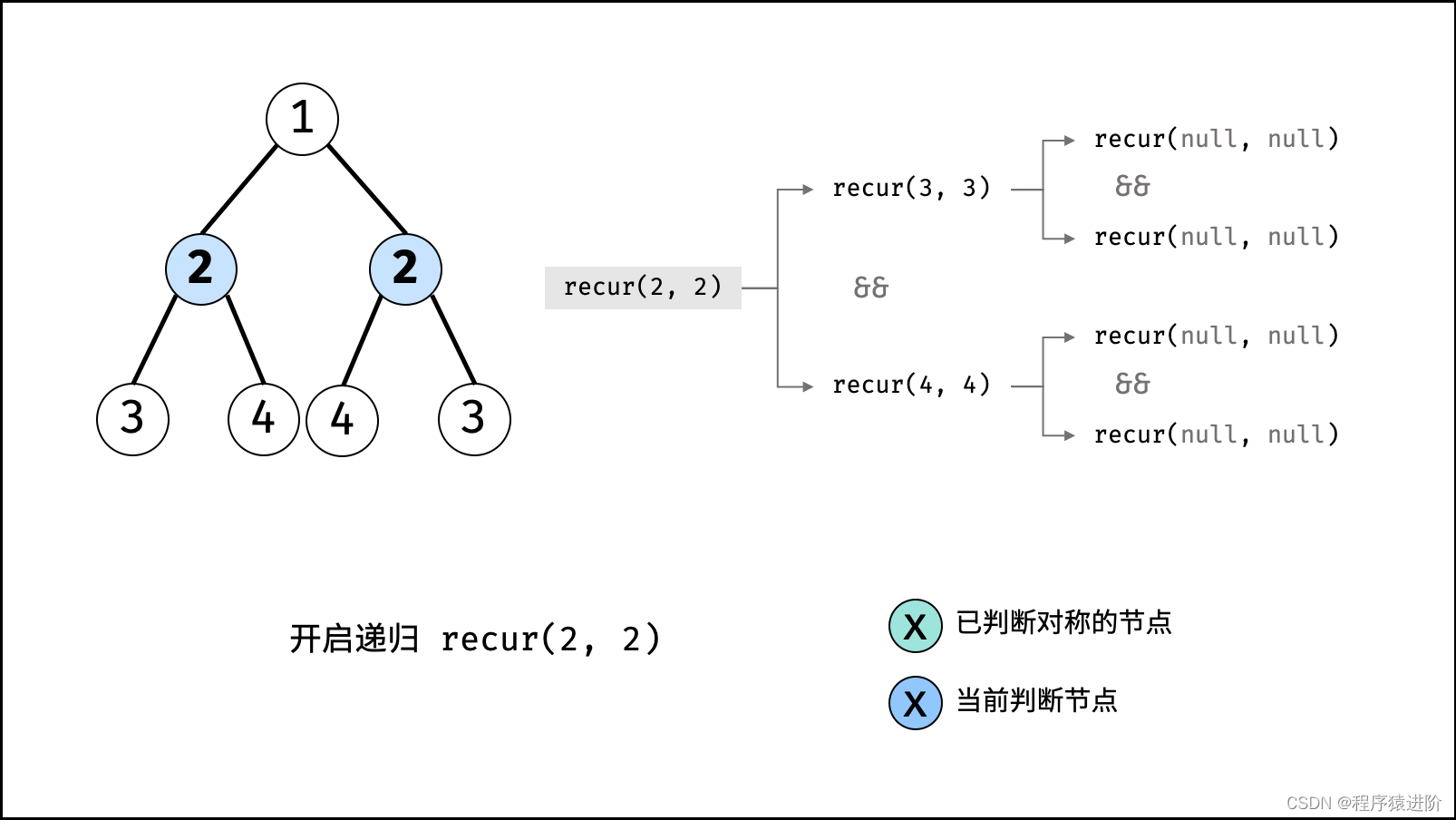
根据以上规律,考虑从顶至底递归,判断每对左右节点是否对称,从而判断树是否为对称二叉树。
算法流程: 函数isSymmetric(root) :
【1】特例处理: 若根节点 root 为空,则直接返回 truetruetrue 。
【2】返回值: 即 recur(root.left, root.right) ;
函数recur(L, R) :
终止条件:
1、当 L 和 R 同时越过叶节点: 此树从顶至底的节点都对称,因此返回 truetruetrue 。
2、当 L 或 R 中只有一个越过叶节点: 此树不对称,因此返回 falsefalsefalse 。
3、当节点 L 值 ≠ 节点 R 值: 此树不对称,因此返回 falsefalsefalse 。
递推工作:
1、判断两节点 L.left 和 R.right 是否对称,即 recur(L.left, R.right) 。
2、判断两节点 L.right 和 R.left 是否对称,即 recur(L.right, R.left) 。
3、返回值: 两对节点都对称时,才是对称树,因此用与逻辑符 && 连接。
class Solution {public boolean isSymmetric(TreeNode root) {return root == null || recur(root.left, root.right);}boolean recur(TreeNode L, TreeNode R) {if (L == null && R == null) return true;if (L == null || R == null || L.val != R.val) return false;return recur(L.left, R.right) && recur(L.right, R.left);}
}
复杂度分析:
时间复杂度O(N) : 其中N为二叉树的节点数量,每次执行recur()可以判断一对节点是否对称,因此最多调用N/2次recur()方法。
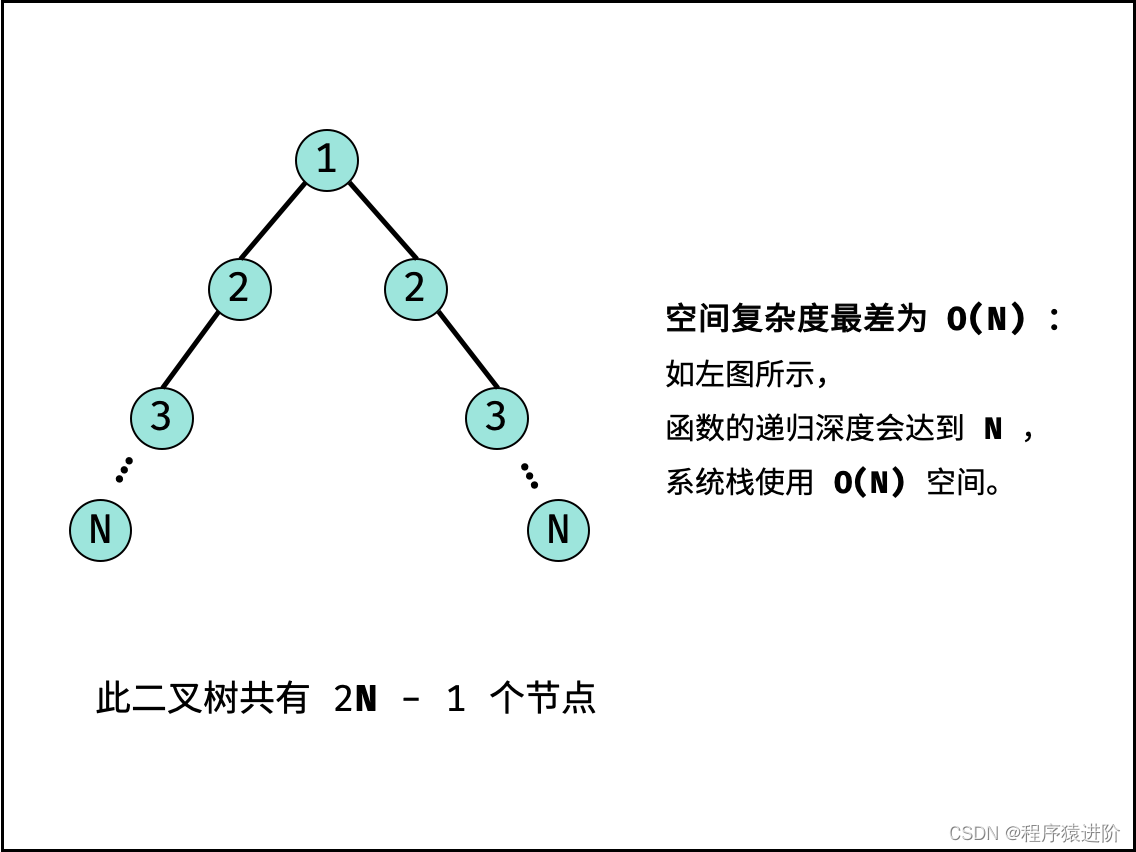
空间复杂度O(N) : 如下图所示,最差情况下(二叉树退化为链表),系统使用O(N)大小的空间。
相关文章:

对称二叉树[简单]
优质博文:IT-BLOG-CN 一、题目 给你一个二叉树的根节点root, 检查它是否轴对称。 示例 1: 输入:root [1,2,2,3,4,4,3] 输出:true 示例 2: 输入:root [1,2,2,null,3,null,3] 输出…...

判断GIF类型并使用ImageDecoder解析GIF图
一、判断是否为GIF图片类型 在JavaScript中,判断用户上传的文件是否为GIF文件类型时,通常可以通过检查文件的type属性或文件的拓展名来判断,但是由于文件拓展名可以轻易被用户修改,type属性是由浏览器根据文件拓展名猜测得出的&a…...

数组对象数据修改后页面没有更新,无法进行编辑,校验失效问题
在 Vue 中,当你通过 Object.assign 或其他方式修改了对象中的某个属性时,Vue 并不会触发组件重新渲染,因此表单中的 input 框无法及时更新。这可能导致在修改表单数据后,页面没有更新,而且表单校验也失效的情况。这是因…...

什么是低代码?有什么特点?
低代码是一种高效的软件开发方法,它允许开发者通过图形化界面和预构建的代码块,以最小化传统手写代码的方式快速构建应用程序。这种方法旨在加速应用程序的开发周期,同时降低技术门槛和成本。以下是根据驰骋低代码设计者的观念与主张…...

Kafka 消息保留时长由 24 小时变更为 72 小时的影响分析
目录 Kafka 消息保留时长由 24 小时变更为 72 小时的影响分析Kafka 消息存储机制保留时长对生产速度的影响保留时长对消费速度的影响底层分析与优化建议附加:将 Kafka 消息保留时长从 24 小时更改为 72 小时后,CPU 使用率从 40% 上升到 70% 的现象1. 增加…...

MySQL A表的字段值更新为B表的字段值
MySQL A表的字段值更新为B表的字段值 准备数据表 create table person (id int unsigned auto_increment comment 主键 primary key,uuid varchar(32) not null comment 系统唯一标识符32个长度的字符串,mobile varchar(11) null comment 中国国内手机号,nickn…...

TCP 建链(三次握手)和断链(四次握手)
TCP 建链(三次握手)和断链(四次挥手) 背景简介建链(三次握手)断链(四次挥手)序号及标志位延伸问题为什么建立连接需要握手三次,两次行不行?三次握手可以携带数…...

SpringBoot集成JOOQ加Mybatis-plus使用@Slf4j日志
遇到个问题记录下,就是SpringBoot使用Mybatis和Mybatis-plus时可以正常打印日志,但是JOOQ的操作日志确打印不出来? 下面的解决方法就是将JOOQ的日志单独配置出来,直接给你们配置吧! 在项目的resources目录下创建日志…...

浅谈JavaScript中的对象赋值
目录 常见的对象赋值方式 直接赋值和对象扩展(浅拷贝)两种赋值方式区别 区别 联系 常见的对象赋值方式 1. 直接赋值:this.info this.deviceInfo,将一个对象的引用赋给另一个变量,它们引用同一个对象。 2. 对象扩…...

Java面试题-集合
Java面试题-集合 1、什么是集合?2、集合和数组的区别是什么?3、集合有哪些特点?4、常用的集合类有哪些?5、List, Set, Map三者的区别?6、说说集合框架底层数据结构?7、线程安全的集合…...
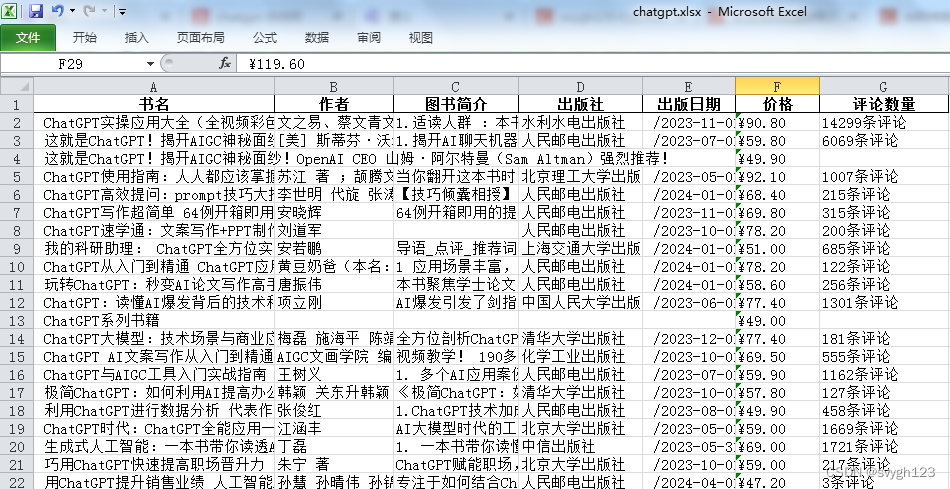
从当当网批量获取图书信息
爬取当当网图书数据并保存到本地,使用request、lxml的etree模块、pandas保存数据为excel到本地。 爬取网页的url为: http://search.dangdang.com/?key{}&actinput&page_index{} 其中key为搜索关键字,page_index为页码。 爬取的数据…...

python爬虫之JS逆向——网页数据解析
目录 一、正则 1 正则基础 元字符 基本使用 通配符: . 字符集: [] 重复 位置 管道符和括号 转义符 转义功能 转义元字符 2 正则进阶 元字符组合(常用) 模式修正符 re模块的方法 有名分组 compile编译 二、bs4 1 四种对象 2 导航文档树 嵌套选择 子节点、…...
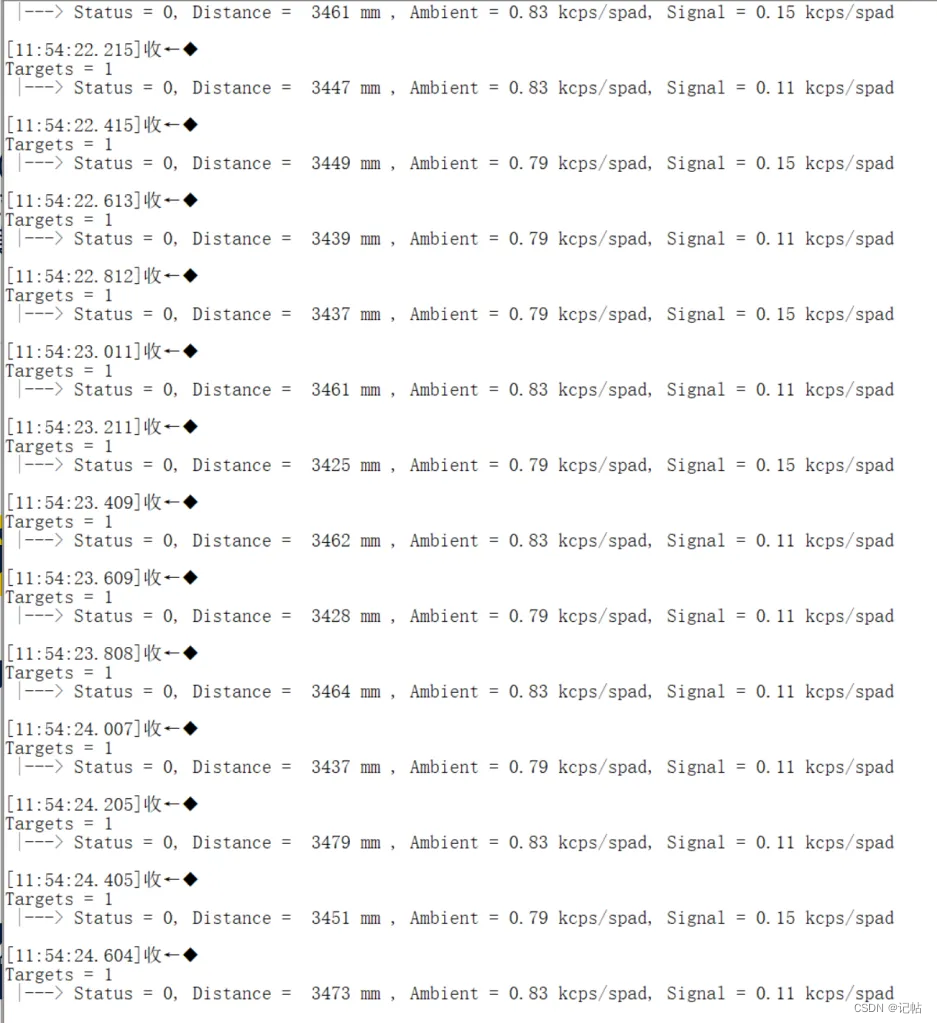
VL53L4CX TOF开发(2)----修改测距范围及测量频率
VL53L4CX TOF开发.2--修改测距范围及测量频率 概述视频教学样品申请完整代码下载测距范围测量频率硬件准备技术规格系统框图应用示意图生成STM32CUBEMX选择MCU串口配置IIC配置 XSHUTGPIO1X-CUBE-TOF1app_tof.c详细解释测量频率修改修改测距范围 概述 最近在弄ST和瑞萨RA的课程…...

C++之noexcept
目录 1.概述 2.noexcept作为说明符 3.noexcept作为运算符 4.传统throw与noexcept比较 5.原理剖析 6.总结 1.概述 在C中,noexcept是一个关键字,用于指定函数不会抛出异常。如果函数保证不会抛出异常,编译器可以进行更多优化,…...
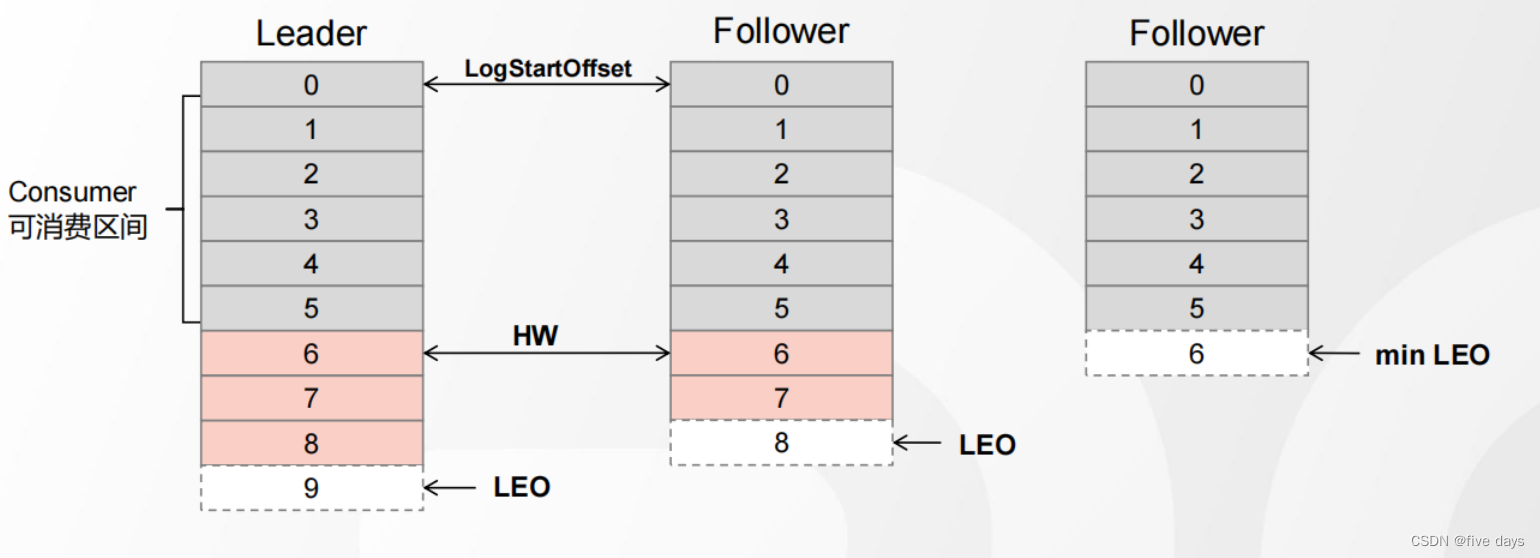
Kafka之Broker原理
1. 日志数据的存储 1.1 Partition 1. 为了实现横向扩展,把不同的数据存放在不同的 Broker 上,同时降低单台服务器的访问压力,我们把一个Topic 中的数据分隔成多个 Partition 2. 每个 Partition 中的消息是有序的,顺序写入&#x…...

RabbitMQ docker安装及使用
1. docker安装RabbitMQ docker下载及配置环境 docker pull rabbitmq:management # 创建用于挂载的目录 mkdir -p /home/docker/rabbitmq/{data,conf,log} # 创建完成之后要对所创建文件授权权限,都设置成777 否则在启动容器的时候容易失败 chmod -R 777 /home/doc…...

篇3:Mapbox Style Specification
接《篇2:Mapbox Style Specification》,继续解读Mapbox Style Specification。 目录 Spec Reference Root 附录: MapBox Terrain-RGB...
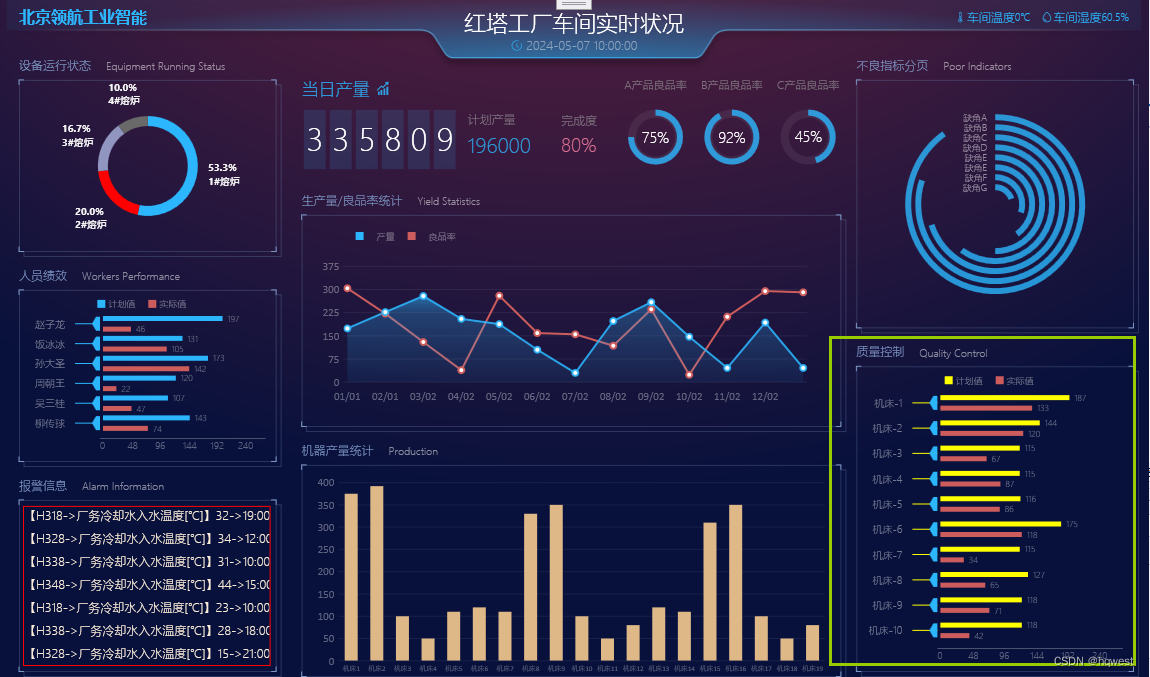
C#WPF数字大屏项目实战11--质量控制
1、区域划分 2、区域布局 3、视图模型 4、控件绑定 5、运行效果 走过路过,不要错过,欢迎点赞,收藏,转载,复制,抄袭,留言,动动你的金手指,财务自由...

第九十七节 Java面向对象设计 - Java Object.Finalize方法
Java面向对象设计 - Java Object.Finalize方法 Java提供了一种在对象即将被销毁时执行资源释放的方法。 在Java中,我们创建对象,但是我们不能销毁对象。 JVM运行一个称为垃圾收集器的低优先级特殊任务来销毁不再引用的所有对象。 垃圾回收器给我们一个…...
【scikit-learn009】异常检测系列:单类支持向量机(OC-SVM)实战总结(看这篇就够了,已更新)
1.一直以来想写下机器学习训练AI算法的系列文章,作为较火的机器学习框架,也是日常项目开发中常用的一款工具,最近刚好挤时间梳理、总结下这块儿的知识体系。 2.熟悉、梳理、总结下scikit-learn框架OCSVM模型相关知识体系。 3.欢迎批评指正,欢迎互三,跪谢一键三连! 4.欢迎…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

aardio 自动识别验证码输入
技术尝试 上周在发学习日志时有网友提议“在网页上识别验证码”,于是尝试整合图像识别与网页自动化技术,完成了这套模拟登录流程。核心思路是:截图验证码→OCR识别→自动填充表单→提交并验证结果。 代码在这里 import soImage; import we…...

【若依】框架项目部署笔记
参考【SpringBoot】【Vue】项目部署_no main manifest attribute, in springboot-0.0.1-sn-CSDN博客 多一个redis安装 准备工作: 压缩包下载:http://download.redis.io/releases 1. 上传压缩包,并进入压缩包所在目录,解压到目标…...
