RabbitMQ docker安装及使用
1. docker安装RabbitMQ
docker下载及配置环境
docker pull rabbitmq:management
# 创建用于挂载的目录
mkdir -p /home/docker/rabbitmq/{data,conf,log}
# 创建完成之后要对所创建文件授权权限,都设置成777 否则在启动容器的时候容易失败
chmod -R 777 /home/docker/rabbitmq
创建临时容器
docker run -d --name rabbitmq --restart=always --hostname=rabbitmqhost \
-e RABBITMQ_DEFAULT_USER=admin -e RABBITMQ_DEFAULT_PASS=Abc1234% \
-e RABBITMQ_DEFAULT_VHOST=my_vhost \
-p 5672:5672 -p 15672:15672 \
rabbitmq:management
** 复制配置文件到宿主机**
docker cp rabbitmq:/etc/rabbitmq/ /home/docker/rabbitmq/conf

删除临时容器
docker stop rabbitmq
docker rm rabbitmq
以文件挂载方式启动rabbitmq镜像
docker run --name rabbitmq \
--restart=always \
-e RABBITMQ_DEFAULT_USER=admin \
-e RABBITMQ_DEFAULT_PASS=Abc1234% \
-v /home/docker/rabbitmq/data:/var/lib/rabbitmq \
-v /home/docker/rabbitmq/conf:/etc/rabbitmq \
-v /home/docker/rabbitmq/log:/var/log/rabbitmq \
-p 5671:5671 \
-p 5672:5672 \
-p 4369:4369 \
-p 15671:15671 \
-p 15672:15672 \
-p 25672:25672 \
-d rabbitmq:management
–restart=always :表示随着Docker容器重启
-e :指定环境变量 RABBITMQ_DEFAULT_VHOST:默认虚拟机名;RABBITMQ_DEFAULT_USER:默认的用户名;RABBITMQ_DEFAULT_PASS:默认用户名的密码,rabbitmq默认账号和密码是guest
--hostname :主机名
-p :端口映射
-v :文件挂载
-d :表示后台运行
–name rabbitmq :表示启动后的容器实例名称为rabbitmq
查看版本
docker image inspect rabbitmq:management|grep -i version

开启后台管理客户端
# 进入rabbitmq容器
docker exec -it rabbitmq sh
# 开启RabbitMQ管理后台
rabbitmq-plugins enable rabbitmq_management
# 添加admin用户:
rabbitmqctl add_user admin password
rabbitmqctl set_user_tags admin administrator
# 退出容器
exit
相关文章:

RabbitMQ docker安装及使用
1. docker安装RabbitMQ docker下载及配置环境 docker pull rabbitmq:management # 创建用于挂载的目录 mkdir -p /home/docker/rabbitmq/{data,conf,log} # 创建完成之后要对所创建文件授权权限,都设置成777 否则在启动容器的时候容易失败 chmod -R 777 /home/doc…...

篇3:Mapbox Style Specification
接《篇2:Mapbox Style Specification》,继续解读Mapbox Style Specification。 目录 Spec Reference Root 附录: MapBox Terrain-RGB...
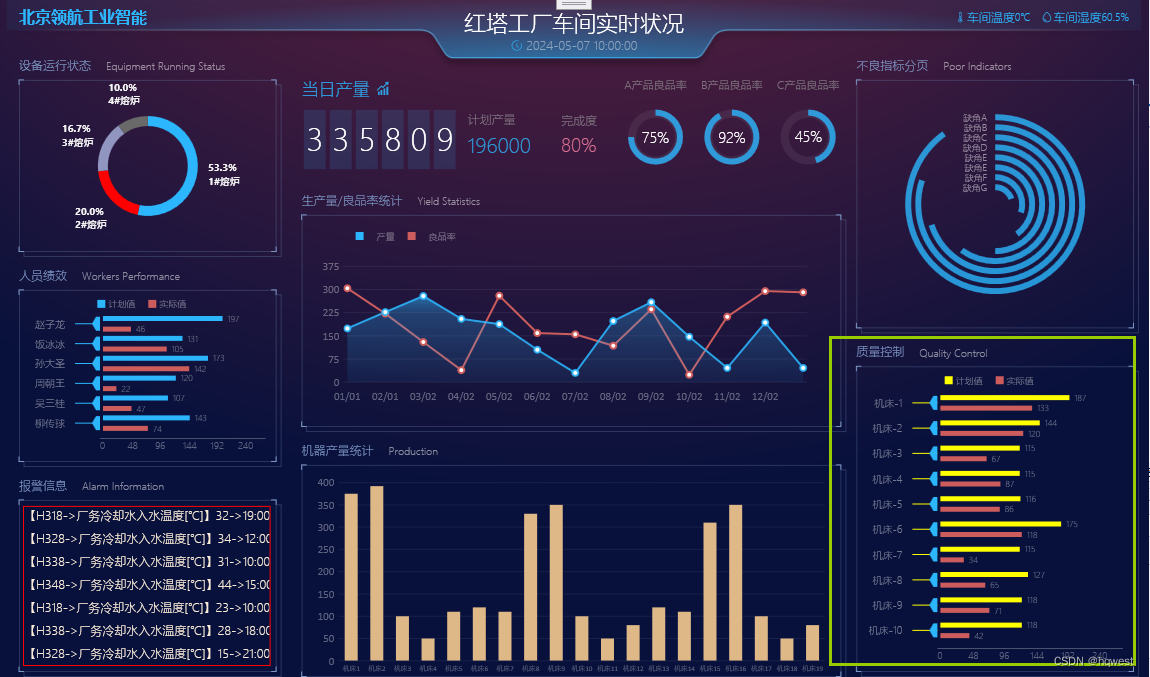
C#WPF数字大屏项目实战11--质量控制
1、区域划分 2、区域布局 3、视图模型 4、控件绑定 5、运行效果 走过路过,不要错过,欢迎点赞,收藏,转载,复制,抄袭,留言,动动你的金手指,财务自由...

第九十七节 Java面向对象设计 - Java Object.Finalize方法
Java面向对象设计 - Java Object.Finalize方法 Java提供了一种在对象即将被销毁时执行资源释放的方法。 在Java中,我们创建对象,但是我们不能销毁对象。 JVM运行一个称为垃圾收集器的低优先级特殊任务来销毁不再引用的所有对象。 垃圾回收器给我们一个…...
【scikit-learn009】异常检测系列:单类支持向量机(OC-SVM)实战总结(看这篇就够了,已更新)
1.一直以来想写下机器学习训练AI算法的系列文章,作为较火的机器学习框架,也是日常项目开发中常用的一款工具,最近刚好挤时间梳理、总结下这块儿的知识体系。 2.熟悉、梳理、总结下scikit-learn框架OCSVM模型相关知识体系。 3.欢迎批评指正,欢迎互三,跪谢一键三连! 4.欢迎…...

网络管理与运维
文章目录 网络管理与运维概念:传统网络管理:基于SNMP集中管理:基于iMaster NCE的网络管理:传统网络管理方式: 基于SNMP集中管理:交互方式:MIB:版本:SNMPv3配置网管平台&a…...

数据库查询字段在哪个数据表中
问题的提出 当DBA运维多个数据库以及多个数据表的时候,联合查询是必不可少的。则数据表的字段名称是需要知道在哪些数据表中存在的。故如下指令,可能会帮助到你: 问题的处理 查找sysinfo这个字段名称都存在哪个数据库中的哪个数据表 SELEC…...

第 400 场 LeetCode 周赛题解
A 候诊室中的最少椅子数 计数:记录室内顾客数,每次顾客进入时,计数器1,顾客离开时,计数器-1 class Solution {public:int minimumChairs(string s) {int res 0;int cnt 0;for (auto c : s) {if (c E)res max(res, …...
数据结构与算法之Floyd弗洛伊德算法求最短路径
目录 前言 Floyd弗洛伊德算法 定义 步骤 一、初始化 二、添加中间点 三、迭代 四、得出结果 时间复杂度 代码实现 结束语 前言 今天是坚持写博客的第18天,希望可以继续坚持在写博客的路上走下去。我们今天来看看数据结构与算法当中的弗洛伊德算法。 Flo…...

Ubuntu系统设置Redis与MySQL登录密码
Ubuntu系统设置Redis与MySQL登录密码 在Ubuntu 20.04系统中配置Redis和MySQL的密码,您需要分别对两个服务进行配置。以下是详细步骤: 配置Redis密码 打开Redis配置文件: Redis的配置文件通常位于/etc/redis/redis.conf。 sudo nano /etc/redis/redis.c…...

数据库连接池的概念和原理
目录 一、什么是数据库连接池 二、数据库连接池的工作原理 1.初始化阶段: 2.获取连接: 3.使用连接: 4.管理和优化: 三、数据库连接池的好处 一、什么是数据库连接池 数据库连接池(Database Connection Pooling&…...

国内常用的编程博客网址:技术资源与学习平台
一、国内常用的编程博客网址:技术资源与学习平台 大家初入编程,肯定会遇到各种各样的问题。我们除了找 AI 工具以外,我们还能怎么迅速解决问题呢? 大家可以通过谷歌,百度,必应,github…...
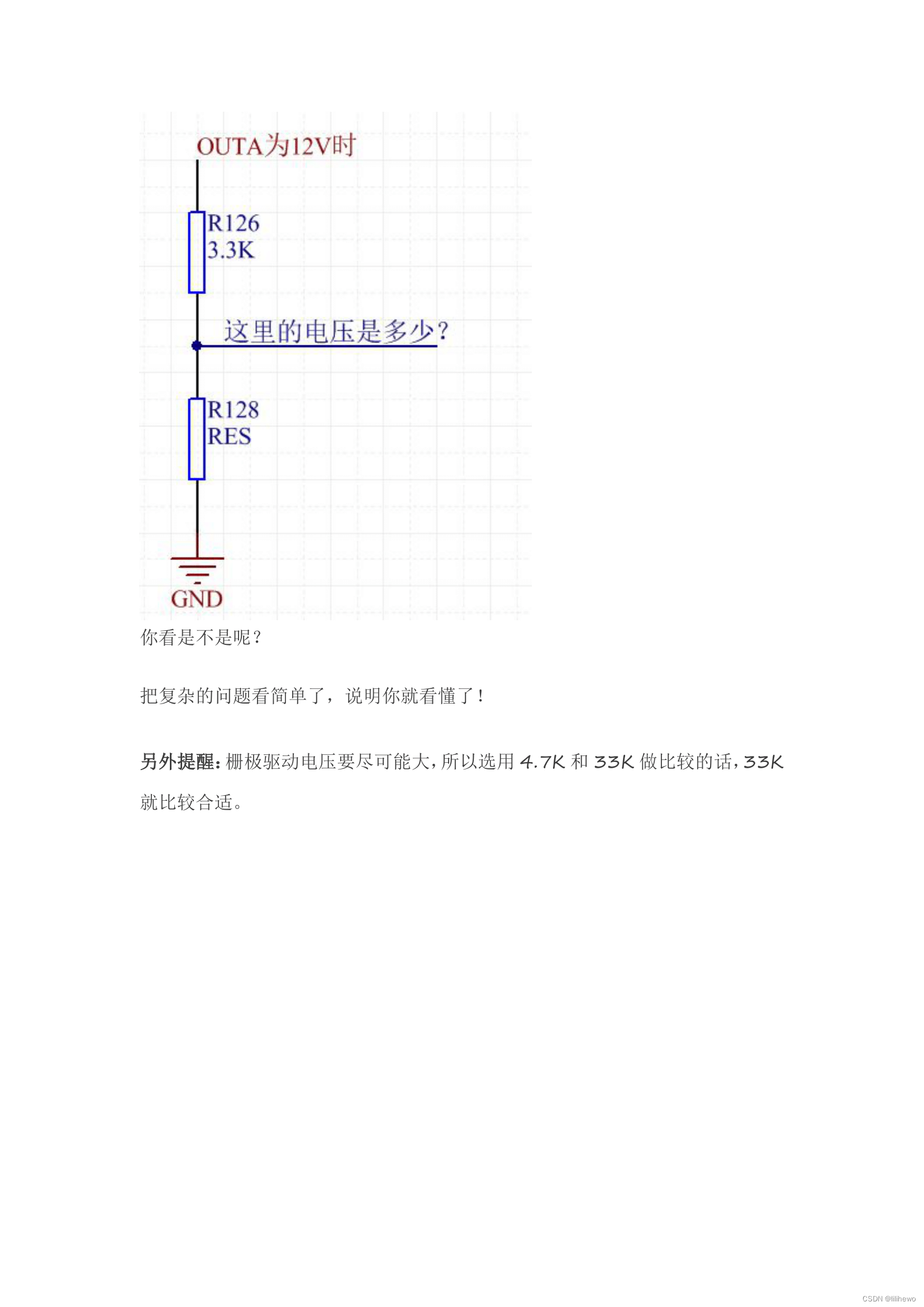
怎么给三极管基极或者MOS管栅极接下拉电阻
文章是瑞生网转载,PDF格式文章下载: 怎么给三极管基极或者MOS管栅极接下拉电阻.pdf: https://url83.ctfile.com/f/45573183-1247189078-52e27b?p7526 (访问密码: 7526)...

Java Web学习笔记5——基础标签和样式
<!DOCTYPE html> html有很多版本,那我们应该告诉用户和浏览器我们现在使用的是HMTL哪个版本。 声明为HTML5文档。 字符集: UTF-8:现在最常用的字符编码方式。 GB2312:简体中文 BIG5:繁体中文、港澳台等方式…...
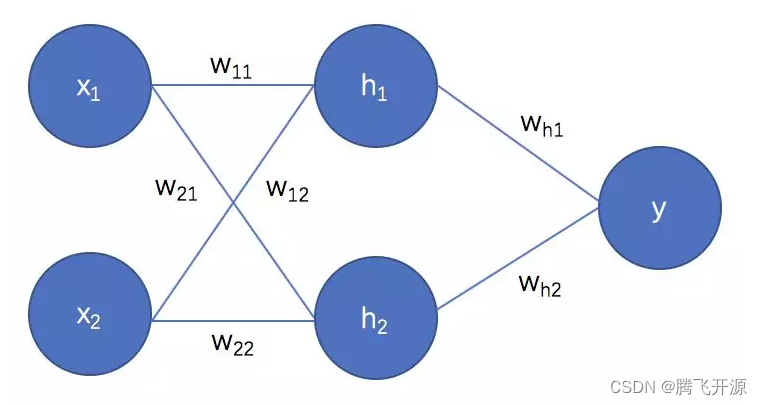
01_深度学习基础知识
1. 感知机 感知机通常情况下指单层的人工神经网络,其结构与 MP 模型类似(按照生物神经元的结构和工作原理造出来的一个抽象和简化了模型,也称为神经网络的一个处理单元) 假设由一个 n 维的单层感知机,则: x 1 x_1 x1 至 x n x_n xn 为 n 维输入向量的各个分量w 1 j…...

60、最大公约数
最大公约数 题目描述 给定n对正整数ai,bi,请你求出每对数的最大公约数。 输入格式 第一行包含整数n。 接下来n行,每行包含一个整数对ai,bi。 输出格式 输出共n行,每行输出一个整数对的最大公约数。 数据范围 1 ≤ n ≤ 1 0 5 , 1≤n≤…...

设计模式在芯片验证中的应用——迭代器
一、迭代器设计模式 迭代器设计模式(iterator)是一种行为设计模式, 让你能在不暴露集合底层表现形式 (列表、 栈和树等数据结构) 的情况下遍历集合中所有的元素。 在验证环境中的checker会收集各个monitor上送过来的transactions࿰…...

imx6ull - 制作烧录SD卡
1、参考NXP官方的手册《i.MX_Linux_Users_Guide.pdf》的这一章节: 1、SD卡分区 提示:我们常用的SD卡一个扇区的大小是512字节。 先说一下i.MX6ULL使用SD卡启动时的分区情况,NXP官方给的镜像布局结构如下所示: 可以看到,…...

使用chatgpt api快速分析pdf
需求背景 搞材料的兄弟经常要分析pdf,然后看到国外有产品是专门调用chatpdf来分析pdf的,所以就来问我能不能帮他也做一个出来。正好我有chatgpt的api,所以就研究了一下这玩意怎么弄。 需求分析 由于chatgpt是按字符算钱的,所以…...

Vue:状态管理pinia
安装 npm install pinia在 main.js 中注册 // main.jsimport { createApp } from vue import { createPinia } from "pinia"; import App from ./app.vueconst app createApp(App) const pinia createPinia(); app.use(pinia).mount(#app)创建 store // stores/…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...
