主成分分析(PCA)原理
主成分分析(PCA)原理
在高维数据处理中,为了简化计算量以及储存空间,需要对这些高维数据进行一定程度上的降维,并尽量保证数据的不失真。PCA和ICA是两种常用的降维方法。
PCA:principal component analysis ,主成分分析
ICA :Independent component analysis,独立成分分析
PCA,ICA都是统计理论当中的概念,在机器学习当中应用很广,比如图像,语音,通信的分析处理。
从线性代数的角度去理解,PCA和ICA都是要找到一组基,这组基张成一个特征空间,数据的处理就都需要映射到新空间中去。
两者常用于机器学习中提取特征后的降维操作。
PCA是找出信号当中的不相关部分(正交性),对应二阶统计量分析。PCA的实现一般有两种,一种是用特征值分解去实现的,一种是用奇异值(SVD)分解去实现。特征值分解也有很多的局限,比如说变换的矩阵必须是方阵,SVD没有这个限制。
PCA的问题其实是一个基的变换,使得变换后的数据有着最大的方差。方差的大小描述的是一个变量的信息量,我们在讲一个东西的稳定性的时候,往往说要减小方差,如果一个模型的方差很大,那就说明模型不稳定了。但是对于我们用于机器学习的数据(主要是训练数据),方差大才有意义,不然输入的数据都是同一个点,那方差就为0了,这样输入的多个数据就等同于一个数据了。

主成分分析(Principal components analysis,以下简称PCA)是最重要的降维方法之一。在数据压缩消除冗余和数据噪音消除等领域都有广泛的应用。一般我们提到降维最容易想到的算法就是PCA,下面我们就对PCA的原理做一个总结。
1. PCA的思想
PCA顾名思义,就是找出数据里最主要的方面,用数据里最主要的方面来代替原始数据。具体的,假如我们的数据集是n维的,共有m个数据(x(1),x(2),...,x(m))(x^{(1)},x^{(2)},...,x^{(m)})(x(1),x(2),...,x(m))。我们希望将这m个数据的维度从n维降到n’维,希望这m个n’维的数据集尽可能的代表原始数据集。我们知道数据从n维降到n’维肯定会有损失,但是我们希望损失尽可能的小。那么如何让这n’维的数据尽可能表示原来的数据呢?
我们先看看最简单的情况,也就是n=2,n’=1,也就是将数据从二维降维到一维。数据如下图。我们希望找到某一个维度方向,它可以代表这两个维度的数据。图中列了两个向量方向,u1u_1u1和u2u_2u2,那么哪个向量可以更好的代表原始数据集呢?从直观上也可以看出,u1u_1u1比u2u_2u2好。

为什么u1u_1u1比u2u_2u2好呢?可以有两种解释,第一种解释是样本点到这个直线的距离足够近,第二种解释是样本点在这个直线上的投影能尽可能的分开。
假如我们把n’从1维推广到任意维,则我们的希望降维的标准为:样本点到这个超平面的距离足够近,或者说样本点在这个超平面上的投影能尽可能的分开。
基于上面的两种标准,我们可以得到PCA的两种等价推导。
2. PCA的推导:基于小于投影距离
我们首先看第一种解释的推导,即样本点到这个超平面的距离足够近。
假设m个n维数据(x(1),x(2),...,x(m))(x^{(1)}, x^{(2)},...,x^{(m)})(x(1),x(2),...,x(m))都已经进行了标准化,即∑i=1mx(i)=0\sum\limits_{i=1}^{m}x^{(i)}=0i=1∑mx(i)=0。经过投影变换后得到的新坐标系为{w1,w2,...,wn}\{w_1,w_2,...,w_n\}{w1,w2,...,wn},其中w是标准正交基,即∣∣w∣∣2=1,wiTwj=0||w||_2=1, w_i^Tw_j=0∣∣w∣∣2=1,wiTwj=0。
如果我们将数据从n维降到n’维,即丢弃新坐标系中的部分坐标,则新的坐标系为{w1,w2,...,wn′}\{w_1,w_2,...,w_{n'}\}{w1,w2,...,wn′},样本点x(i)x^{(i)}x(i)在n’维坐标系中的投影为:z(i)=(z1(i),z2(i),...,zn′(i))z^{(i)} = (z_1^{(i)}, z_2^{(i)},...,z_{n'}^{(i)})z(i)=(z1(i),z2(i),...,zn′(i)).其中,zj(i)=wjTx(i)z_j^{(i)} = w_j^Tx^{(i)}zj(i)=wjTx(i)是x(i)x^{(i)}x(i)在低维坐标系里第j维的坐标。
如果我们用z(i)z^{(i)}z(i)来恢复原始数据x(i)x^{(i)}x(i),则得到的恢复数据x‾(i)=∑j=1n′zj(i)wj=Wz(i)\overline{x}^{(i)} = \sum\limits_{j=1}^{n'}z_j^{(i)}w_j = Wz^{(i)}x(i)=j=1∑n′zj(i)wj=Wz(i),其中,W为标准正交基组成的矩阵。
现在我们考虑整个样本集,我们希望所有的样本到这个超平面的距离足够近,即最小化下式:∑i=1m∣∣x‾(i)−x(i)∣∣22\sum\limits_{i=1}^{m}||\overline{x}^{(i)} - x^{(i)}||_2^2i=1∑m∣∣x(i)−x(i)∣∣22
将这个式子进行整理,可以得到:
∑i=1m∣∣x‾(i)−x(i)∣∣22=∑i=1m∣∣Wz(i)−x(i)∣∣22=∑i=1m(Wz(i))T(Wz(i))−2∑i=1m(Wz(i))Tx(i)+∑i=1mx(i)Tx(i)=∑i=1mz(i)Tz(i)−2∑i=1mz(i)TWTx(i)+∑i=1mx(i)Tx(i)=∑i=1mz(i)Tz(i)−2∑i=1mz(i)Tz(i)+∑i=1mx(i)Tx(i)=−∑i=1mz(i)Tz(i)+∑i=1mx(i)Tx(i)=−tr(WT(∑i=1mx(i)x(i)T)W)+∑i=1mx(i)Tx(i)=−tr(WTXXTW)+∑i=1mx(i)Tx(i)\begin{aligned} \sum\limits_{i=1}^{m}||\overline{x}^{(i)} - x^{(i)}||_2^2 & = \sum\limits_{i=1}^{m}|| Wz^{(i)} - x^{(i)}||_2^2 \\& = \sum\limits_{i=1}^{m}(Wz^{(i)})^T(Wz^{(i)}) - 2\sum\limits_{i=1}^{m}(Wz^{(i)})^Tx^{(i)} + \sum\limits_{i=1}^{m} x^{(i)T}x^{(i)} \\& = \sum\limits_{i=1}^{m}z^{(i)T}z^{(i)} - 2\sum\limits_{i=1}^{m}z^{(i)T}W^Tx^{(i)} +\sum\limits_{i=1}^{m} x^{(i)T}x^{(i)} \\& = \sum\limits_{i=1}^{m}z^{(i)T}z^{(i)} - 2\sum\limits_{i=1}^{m}z^{(i)T}z^{(i)}+\sum\limits_{i=1}^{m} x^{(i)T}x^{(i)} = - \sum\limits_{i=1}^{m}z^{(i)T}z^{(i)} + \sum\limits_{i=1}^{m} x^{(i)T}x^{(i)} \\& = -tr(W^T(\sum\limits_{i=1}^{m}x^{(i)}x^{(i)T})W) + \sum\limits_{i=1}^{m} x^{(i)T}x^{(i)} = -tr( W^TXX^TW) + \sum\limits_{i=1}^{m} x^{(i)T}x^{(i)} \end{aligned}i=1∑m∣∣x(i)−x(i)∣∣22=i=1∑m∣∣Wz(i)−x(i)∣∣22=i=1∑m(Wz(i))T(Wz(i))−2i=1∑m(Wz(i))Tx(i)+i=1∑mx(i)Tx(i)=i=1∑mz(i)Tz(i)−2i=1∑mz(i)TWTx(i)+i=1∑mx(i)Tx(i)=i=1∑mz(i)Tz(i)−2i=1∑mz(i)Tz(i)+i=1∑mx(i)Tx(i)=−i=1∑mz(i)Tz(i)+i=1∑mx(i)Tx(i)=−tr(WT(i=1∑mx(i)x(i)T)W)+i=1∑mx(i)Tx(i)=−tr(WTXXTW)+i=1∑mx(i)Tx(i)
其中第(1)步用到了x‾(i)=Wz(i)\overline{x}^{(i)}=Wz^{(i)}x(i)=Wz(i),第(2)步用到了平方和展开,第(3)步用到了矩阵转置公式(AB)T=BTAT(AB)^T =B^TA^T(AB)T=BTAT和WTW=IW^TW=IWTW=I,第(4)步用到了z(i)=WTx(i)z^{(i)}=W^Tx^{(i)}z(i)=WTx(i),第(5)步合并同类项,第(6)步用到了z(i)=WTx(i)z^{(i)}=W^Tx^{(i)}z(i)=WTx(i)和矩阵的迹,第(7)步将代数和表达为矩阵形式。
注意到∑i=1mx(i)x(i)T\sum\limits_{i=1}^{m}x^{(i)}x^{(i)T}i=1∑mx(i)x(i)T是数据集的协方差矩阵,W的每一个向量wjw_jwj是标准正交基。而∑i=1mx(i)Tx(i)\sum\limits_{i=1}^{m} x^{(i)T}x^{(i)}i=1∑mx(i)Tx(i)是一个常量。最小化上式等价于:
argmin−tr(WTXXTW)arg min-tr( W^TXX^TW) argmin−tr(WTXXTW)
s.t.WTW=Is.t. W^TW=I s.t.WTW=I
这个最小化不难,直接观察也可以发现最小值对应的W由协方差矩阵XXTXX^TXXT最大的n’个特征值对应的特征向量组成。当然用数学推导也很容易。利用拉格朗日函数可以得到J(W)=−tr(WTXXTW)+λ(WTW−I)J(W) = -tr( W^TXX^TW) + \lambda(W^TW-I)J(W)=−tr(WTXXTW)+λ(WTW−I)
对W求导有−XXTW+λW=0-XX^TW+\lambda W=0−XXTW+λW=0, 整理下即为:XXTW=λWXX^TW=\lambda WXXTW=λW
这样可以更清楚的看出,W为XXTXX^TXXT的n’个特征向量组成的矩阵,而λ\lambdaλ为XXTXX^TXXT的特征值。当我们将数据集从n维降到n’维时,需要找到最大的n’个特征值对应的特征向量。这n’个特征向量组成的矩阵W即为我们需要的矩阵。对于原始数据集,我们只需要用z(i)=WTx(i)z^{(i)}=W^Tx^{(i)}z(i)=WTx(i),就可以把原始数据集降维到最小投影距离的n’维数据集。
如果你熟悉谱聚类的优化过程,就会发现和PCA的非常类似,只不过谱聚类是求前k个最小的特征值对应的特征向量,而PCA是求前k个最大的特征值对应的特征向量。
3. PCA的推导:基于最大投影方差
现在我们再来看看基于最大投影方差的推导。
假设m个n维数据(x(1),x(2),...,x(m))(x^{(1)}, x^{(2)},...,x^{(m)})(x(1),x(2),...,x(m))都已经进行了标准化,即∑i=1mx(i)=0\sum\limits_{i=1}^{m}x^{(i)}=0i=1∑mx(i)=0。经过投影变换后得到的新坐标系为{w1,w2,...,wn}\{w_1,w_2,...,w_n\}{w1,w2,...,wn},其中w是标准正交基,即∣∣w∣∣2=1,wiTwj=0||w||_2=1, w_i^Tw_j=0∣∣w∣∣2=1,wiTwj=0。
如果我们将数据从n维降到n’维,即丢弃新坐标系中的部分坐标,则新的坐标系为{w1,w2,...,wn′}\{w_1,w_2,...,w_{n'}\}{w1,w2,...,wn′},样本点x(i)x^{(i)}x(i)在n’维坐标系中的投影为:z(i)=(z1(i),z2(i),...,zn′(i))z^{(i)} = (z_1^{(i)}, z_2^{(i)},...,z_{n'}^{(i)})z(i)=(z1(i),z2(i),...,zn′(i)).其中,zj(i)=wjTx(i)z_j^{(i)} = w_j^Tx^{(i)}zj(i)=wjTx(i)是x(i)x^{(i)}x(i)在低维坐标系里第j维的坐标。
对于任意一个样本x(i)x^{(i)}x(i),在新的坐标系中的投影为WTx(i)W^Tx^{(i)}WTx(i),在新坐标系中的投影方差为WTx(i)x(i)TWW^Tx^{(i)}x^{(i)T}WWTx(i)x(i)TW,要使所有的样本的投影方差和最大,也就是最大化∑i=1mWTx(i)x(i)TW\sum\limits_{i=1}^{m}W^Tx^{(i)}x^{(i)T}Wi=1∑mWTx(i)x(i)TW,即:argmaxtr(WTXXTW)s.t.WTW=Iargmax \;\;tr( W^TXX^TW) \;\;s.t. W^TW=Iargmaxtr(WTXXTW)s.t.WTW=I
观察第二节的基于最小投影距离的优化目标,可以发现完全一样,只是一个是加负号的最小化,一个是最大化。
利用拉格朗日函数可以得到J(W)=tr(WTXXTW)+λ(WTW−I)J(W) = tr( W^TXX^TW) + \lambda(W^TW-I)J(W)=tr(WTXXTW)+λ(WTW−I)
对W求导有XXTW+λW=0XX^TW+\lambda W=0XXTW+λW=0, 整理下即为:XXTW=(−λ)WXX^TW=(-\lambda)WXXTW=(−λ)W
和上面一样可以看出,W为XXTXX^TXXT的n’个特征向量组成的矩阵,而−λ-\lambda−λ为XXTXX^TXXT的特征值。当我们将数据集从n维降到n’维时,需要找到最大的n’个特征值对应的特征向量。这n’个特征向量组成的矩阵W即为我们需要的矩阵。对于原始数据集,我们只需要用z(i)=WTx(i)z^{(i)}=W^Tx^{(i)}z(i)=WTx(i),就可以把原始数据集降维到最小投影距离的n’维数据集。
4. PCA算法流程
从上面两节我们可以看出,求样本x(i)x^{(i)}x(i)的n’维的主成分其实就是求样本集的协方差矩阵XXTXX^TXXT的前n’个特征值对应特征向量矩阵W,然后对于每个样本x(i)x^{(i)}x(i),做如下变换z(i)=WTx(i)z^{(i)}=W^Tx^{(i)}z(i)=WTx(i),即达到降维的PCA目的。
下面我们看看具体的算法流程。
输入:n维样本集D=(x(1),x(2),...,x(m))D=(x^{(1)}, x^{(2)},...,x^{(m)})D=(x(1),x(2),...,x(m)),要降维到的维数n’.
输出:降维后的样本集D’
1) 对所有的样本进行中心化:x(i)=x(i)−1m∑j=1mx(j)x^{(i)} = x^{(i)} - \frac{1}{m}\sum\limits_{j=1}^{m} x^{(j)}x(i)=x(i)−m1j=1∑mx(j)
2) 计算样本的协方差矩阵XXTXX^TXXT
3) 对矩阵XXTXX^TXXT进行特征值分解
4)取出最大的n’个特征值对应的特征向量(w1,w2,...,wn′)(w_1,w_2,...,w_{n'})(w1,w2,...,wn′), 将所有的特征向量标准化后,组成特征向量矩阵W。
5)对样本集中的每一个样本x(i)x^{(i)}x(i),转化为新的样本z(i)=WTx(i)z^{(i)}=W^Tx^{(i)}z(i)=WTx(i)
6) 得到输出样本集D′=(z(1),z(2),...,z(m))D' =(z^{(1)}, z^{(2)},...,z^{(m)})D′=(z(1),z(2),...,z(m))
有时候,我们不指定降维后的n’的值,而是换种方式,指定一个降维到的主成分比重阈值t。这个阈值t在(0,1]之间。假如我们的n个特征值为λ1≥λ2≥...≥λn\lambda_1 \geq \lambda_2 \geq ... \geq \lambda_nλ1≥λ2≥...≥λn,则n’可以通过下式得到:∑i=1n′λi∑i=1nλi≥t\frac{\sum\limits_{i=1}^{n'}\lambda_i}{\sum\limits_{i=1}^{n}\lambda_i} \geq ti=1∑nλii=1∑n′λi≥t
5. PCA实例
下面举一个简单的例子,说明PCA的过程。
假设我们的数据集有10个二维数据(2.5,2.4), (0.5,0.7), (2.2,2.9), (1.9,2.2), (3.1,3.0), (2.3, 2.7), (2, 1.6), (1, 1.1), (1.5, 1.6), (1.1, 0.9),需要用PCA降到1维特征。
首先我们对样本中心化,这里样本的均值为(1.81, 1.91),所有的样本减去这个均值后,即中心化后的数据集为(0.69, 0.49), (-1.31, -1.21), (0.39, 0.99), (0.09, 0.29), (1.29, 1.09), (0.49, 0.79), (0.19, -0.31), (-0.81, -0.81), (-0.31, -0.31), (-0.71, -1.01)。
现在我们开始求样本的协方差矩阵,由于我们是二维的,则协方差矩阵为:
XXT=(cov(x1,x1)cov(x1,x2)cov(x2,x1)cov(x2,x2))\mathbf{XX^T} = \left( \begin{array}{ccc} cov(x_1,x_1) & cov(x_1,x_2)\\ cov(x_2,x_1) & cov(x_2,x_2) \end{array} \right)XXT=(cov(x1,x1)cov(x2,x1)cov(x1,x2)cov(x2,x2))
对于我们的数据,求出协方差矩阵为:
XXT=(0.6165555560.6154444440.6154444440.716555556)\mathbf{XX^T} = \left( \begin{array}{ccc} 0.616555556 & 0.615444444\\ 0.615444444 & 0.716555556 \end{array} \right)XXT=(0.6165555560.6154444440.6154444440.716555556)
求出特征值为(0.490833989, 1.28402771),对应的特征向量分别为:(0.735178656,0.677873399)T(−0.677873399,−0.735178656)T(0.735178656, 0.677873399)^T\;\; (-0.677873399, -0.735178656)^T(0.735178656,0.677873399)T(−0.677873399,−0.735178656)T,由于最大的k=1个特征值为1.28402771,对于的k=1个特征向量为(−0.677873399,−0.735178656)T(-0.677873399, -0.735178656)^T(−0.677873399,−0.735178656)T. 则我们的W=(−0.677873399,−0.735178656)TW=(-0.677873399, -0.735178656)^TW=(−0.677873399,−0.735178656)T
我们对所有的数据集进行投影z(i)=WTx(i)z^{(i)}=W^Tx^{(i)}z(i)=WTx(i),得到PCA降维后的10个一维数据集为:(-0.827970186, 1.77758033, -0.992197494, -0.274210416, -1.67580142, -0.912949103, 0.0991094375, 1.14457216, 0.438046137, 1.22382056)
6. 核主成分分析KPCA介绍
在上面的PCA算法中,我们假设存在一个线性的超平面,可以让我们对数据进行投影。但是有些时候,数据不是线性的,不能直接进行PCA降维。这里就需要用到和支持向量机一样的核函数的思想,先把数据集从n维映射到线性可分的高维N>n,然后再从N维降维到一个低维度n’, 这里的维度之间满足n’<n<N。
使用了核函数的主成分分析一般称之为核主成分分析(Kernelized PCA, 以下简称KPCA。假设高维空间的数据是由n维空间的数据通过映射ϕ\phiϕ产生。
则对于n维空间的特征分解:∑i=1mx(i)x(i)TW=λW\sum\limits_{i=1}^{m}x^{(i)}x^{(i)T}W=\lambda Wi=1∑mx(i)x(i)TW=λW
映射为:∑i=1mϕ(x(i))ϕ(x(i))TW=λW\sum\limits_{i=1}^{m}\phi(x^{(i)})\phi(x^{(i)})^TW=\lambda Wi=1∑mϕ(x(i))ϕ(x(i))TW=λW
通过在高维空间进行协方差矩阵的特征值分解,然后用和PCA一样的方法进行降维。一般来说,映射ϕ\phiϕ不用显式的计算,而是在需要计算的时候通过核函数完成。由于KPCA需要核函数的运算,因此它的计算量要比PCA大很多。
7. PCA算法总结
这里对PCA算法做一个总结。作为一个非监督学习的降维方法,它只需要特征值分解,就可以对数据进行压缩,去噪。因此在实际场景应用很广泛。为了克服PCA的一些缺点,出现了很多PCA的变种,比如为解决非线性降维的KPCA,还有解决内存限制的增量PCA方法Incremental PCA,以及解决稀疏数据降维的PCA方法Sparse PCA等。
PCA算法的主要优点有:
1)仅仅需要以方差衡量信息量,不受数据集以外的因素影响。
2)各主成分之间正交,可消除原始数据成分间的相互影响的因素。
3)计算方法简单,主要运算是特征值分解,易于实现。
PCA算法的主要缺点有:
1)主成分各个特征维度的含义具有一定的模糊性,不如原始样本特征的解释性强。
2)方差小的非主成分也可能含有对样本差异的重要信息,因降维丢弃可能对后续数据处理有影响。
相关文章:

主成分分析(PCA)原理
主成分分析(PCA)原理 在高维数据处理中,为了简化计算量以及储存空间,需要对这些高维数据进行一定程度上的降维,并尽量保证数据的不失真。PCA和ICA是两种常用的降维方法。 PCA:principal component analysi…...

Git:合并一个仓库的某个分支到另一个仓库的某个分支
ps:(同名分支或不同名分支均可) 1.操作: 当前仓库A的一个指定分支1 推给 另一个仓库B的另一个指定分支2 仓库A:repo1 分支1:develop1 仓库B:repo2 分支2:develop2 2.操作命令: 1、git pull # 在当前仓…...
工作记录:bi重构
2023.3.8,我在组内进行工作汇报。内容记录如下: 本次重构的特点 改动大影响后续开发 所以有必要进行工作汇报,让组内同事了解代码的改动与现状。 为什么要重构代码? 正在开发的数据报告模块包含大量 widget 功能,…...
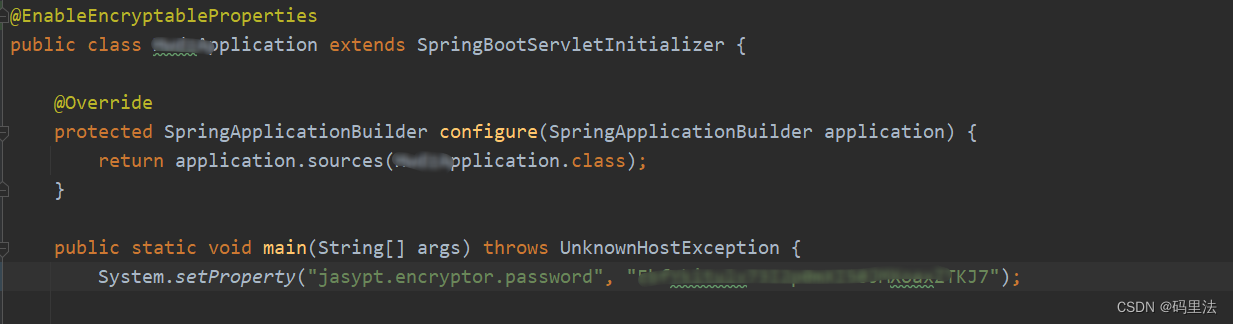
java明文数据加密、脱敏方法总结
前言 在一些安全性要求比较高的项目里,避免不了要对敏感信息进行加解密,比如配置文件中的敏感信息。 第一种方法(自定义加解密) 加解密工具类: public class SecurityTools {public static final String ALGORITHM…...

4N65-ASEMI高压MOS管4N65
编辑-Z 4N65在TO-220封装里的静态漏极源导通电阻(RDS(ON))为2.5Ω,是一款N沟道高压MOS管。4N65的最大脉冲正向电流ISM为16A,零栅极电压漏极电流(IDSS)为10uA,其工作时耐温度范围为-55~150摄氏度。4N65功耗(…...
)
天梯赛训练L1-018 (大笨钟)
目录 1、L1-018 大笨钟 2、 如果到帮助大家,希望大家一键三连!!! 1、L1-018 大笨钟 分数 10 题目通道 微博上有个自称“大笨钟V”的家伙,每天敲钟催促码农们爱惜身体早点睡觉。不过由于笨钟自己作息也不是很规律&a…...

GCC编译器编译C/C++程序(一步完成、分步完成)
以下内容源于C语言中文网的学习与整理,非原创,如有侵权请告知删除。 参考内容 (1)GCC 预处理器选项_dllbl的博客-CSDN博客 (2)Preprocessor Options (Using the GNU Compiler Collection (GCC)) 一、编译的…...

Java8中那些方便又实用的Map函数
简介 java8之后,常用的Map接口中添加了一些非常实用的函数,可以大大简化一些特定场景的代码编写,提升代码可读性,一起来看看吧。 computeIfAbsent函数 比如,很多时候我们需要对数据进行分组,变成Map<…...

如何修复dxgi.dll文件错误?修复方法推荐
如果您使用Windows操作系统,在使用某些应用程序时,可能会遇到dxgi.dll文件错误。这可能会导致应用程序崩溃或无法正常运行。在本文中,我们将探讨如何修复dxgi.dll文件错误。 一.什么是dxgi.dll文件 dxgi.dll文件是Microsoft DirectX图形接口…...

数字化时代,你应该知道的BI
我曾经看到有人在讨论过商业智能BI的部署对于企业是否有实际意义,现在市场的数据已经证明商业智能BI在商业世界中,在企业的实践中证明了自己的价值,得到了广泛的认可。 一、什么是BI 有一点可能很多人没有想到,实际上商业智能BI…...

前端jQuery ajax请求,后端node.js使用cors跨域
前言 跨域,一句话介绍: 你要请求的URL地址与当前的URL地址,协议不同、域名不同、端口不同时,就是跨域。 步入正题 前端,jQuery ajax请求 $.ajax({async: false,method: post,//URl和端口与后台匹配好,当…...

【最重要的 G 代码命令列表】
【最重要的 G 代码命令列表】1. 什么是G代码?2. 如何阅读G代码命令?3. 最重要/最常见的 G 代码命令3.1 G00 – 快速定位3.2 G01 – 线性插值3.3 G02 – 顺时针圆形插值3.4 G00、G01、G02 示例 – 手动 G 代码编程3.4 G03 – 逆时针圆形插补3.5 G20/ G21 …...

好用的公共DNS地址共享
公共DNS服务器地址大全 服务商云公共DNS服务器IP大全114DNS114.114.114.114114.114.115.115DNSPod DNS+119.29.29.29182.254.116.1162402:4e00::DNS 派 电信/移动/铁通101.226.4.6218.30.118.6DNS 派 联通123.125.81.6140.207.198.6cnnicDNS1.2.4.8210.2.4.82001:dc7:1000::1Go…...
C#:Krypton控件使用方法详解(第十三讲) ——kryptonDomainUpDown
今天介绍的Krypton控件中的kryptonDomainUpDown。下面介绍控件的外观属性和Item属性:Cursor属性:表示鼠标移动过该控件的时候,鼠标显示的形状。属性值如下图所示:Text属性:表示控件的显示文本内容,属性值为…...
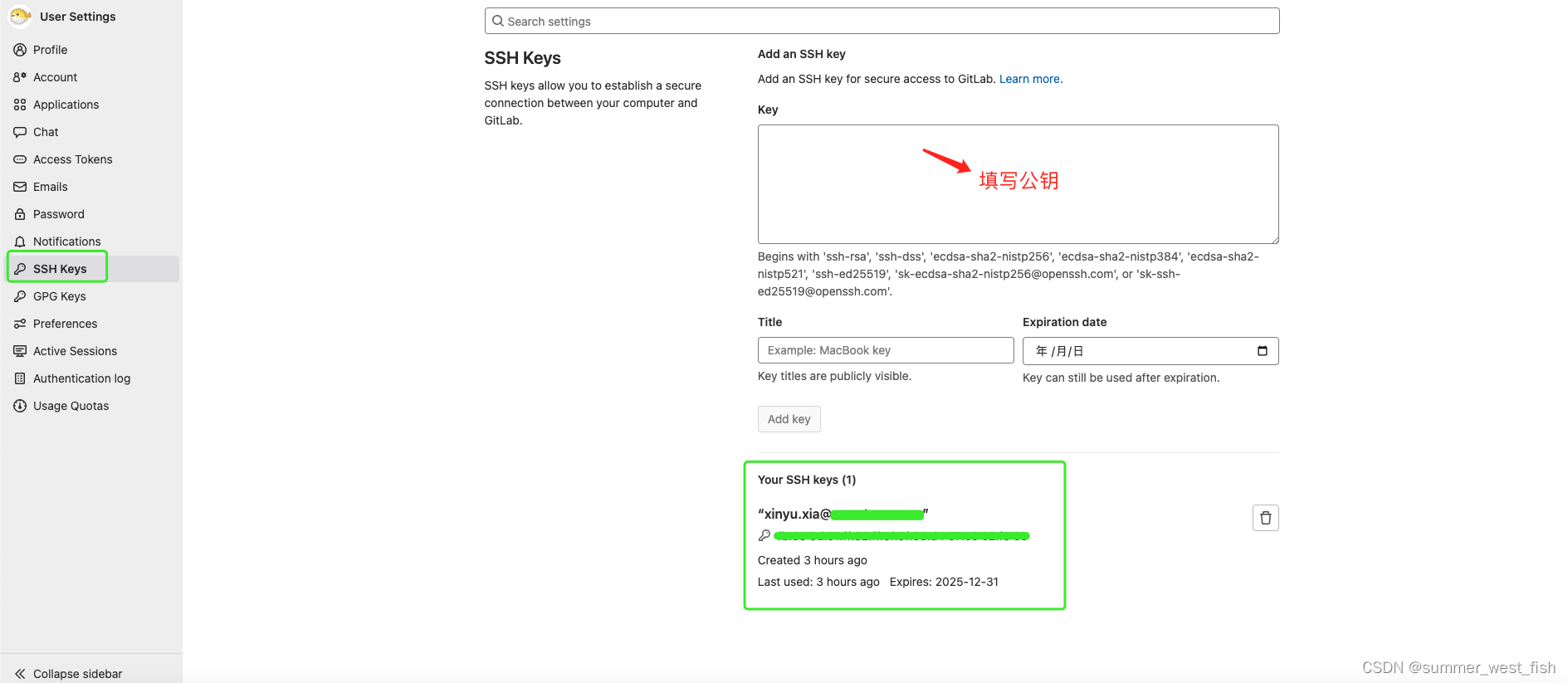
Git设置SSH Key
一、git 配置 (1)打开 git 命令窗口 (2)配置用户名(填自己的姓名) git config --global user.name “xinyu.xia” (3)配置用户邮箱(填自己的邮箱࿰…...

WireShark如何抓包,各种协议(HTTP、ARP、ICMP)的过滤或分析,用WireShark实现TCP三次握手和四次挥手
WireShark一、开启WireShark的大门二、如何抓包 搜索关键字2.1 协议过滤2.2 IP过滤2.3 过滤端口2.4 过滤MAC地址2.5 过滤包长度2.6 HTTP模式过滤三、ARP协议分析四、WireShark之ICMP协议五、TCP三次握手与四次挥手5.1 TCP三次握手实验5.2 可视化看TCP三次握手5.3 TCP四次挥手5.…...
熬夜30天吃透这九大Java核心专题,我收割了3个大厂offer
这次一共收割了3个大厂offer,分别是蚂蚁金服、美团和网易,特意分享这次对我帮助非常大的宝典资料,一共涉及九大核心专题,分别是计算机网络、操作系统、MySQL、Linux、JAVA、JVM、Redis、消息队列与分布式、网站优化相关࿰…...

DMHS搭建DMDSC 2节点集群同步到单库
DMHS搭建DMDSC 2节点集群同步到单库环境介绍1 安装DMOCI1.1 关闭数据库实例服务1.2 将DMOCI 复制到源端与目的端的数据库bin目录1.3 对数据库bin 执行目录文件更改用户属组和权限2 启动源数据库服务并配置数据库实例参数2.1 使用DMCSSM启动集群实例2.2 DMDSC源其中一个节点执行…...

一条sql执行很慢可能的原因,如何优化
文章目录 sql怎么会变慢呢?1、大多数情况下很正常,偶尔很慢,则有如下原因2、这条 SQL 语句一直执行的很慢,则有如下原因:慢sql优化数据库中设置SQL慢查询分析慢查询日志慢sql如何让优化索引sql语句1、分页查询优化2、优化insert语句数据库结构优化优化器优化架构优化总结s…...
【设计模式】适配器模式和桥接模式
适配器模式 适配器模式 : 就是将一个类的接口变成客户端所期望的另一种接口,使得原本因为接口不匹配而无法一起工作的接口可以正常工作。属于结构型模式 比方说我有一个A牌子的奶瓶,然后买了个B牌子的奶嘴,不能匹配怎么办? 再买一个转换器…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...
