十大排序 —— 希尔排序
十大排序 —— 希尔排序
- 什么是希尔排序
- 插入排序
- 希尔排序
- 递归版本
我们今天来看另一个很有名的排序——希尔排序
什么是希尔排序
希尔排序(Shell Sort)是插入排序的一种更高效的改进版本,由Donald Shell于1959年提出。它通过比较相距一定间隔的元素来工作,间隔会逐步减小,直到最后变成1,此时算法实际上退化为普通的插入排序,但因为数组元素基本已经部分排序,所以插入排序在这个阶段会非常高效。
希尔排序的基本思想是将原始数据集分割成若干子序列,先使这些子序列基本有序,然后再对全体记录进行一次直接插入排序。这里的"基本有序"是指在子序列内,任意两个元素之间的距离都不超过某个预先设定的间隔(称为"增量"或"gap")时,它们的顺序要么是正确的,要么仅需很少的比较和移动就可以变得正确。
希尔排序的具体步骤如下:
- 选择一个增量序列:首先确定一个增量
gap,常见的选择有希尔增量(如gap = gap / 2,直到gap = 1),或者使用更复杂的序列如Hibbard增量序列。- 分组排序:将整个数组分成多个子序列,每个子序列包含相距
gap的元素,然后对每个子序列应用插入排序。- 减小增量:重复步骤1和2,但每次减小增量的大小,直到增量为1。
- 最终排序:当增量减至1时,整个数组就是一个子序列,对这个子序列执行插入排序,这时数组应该是(或接近)完全有序。
希尔排序的优势在于它能够较早地将远处的元素移动到更接近其最终位置,从而减少了数据移动的总次数,提高了排序效率。特别是在数组规模较大时,相比简单的插入排序,希尔排序能显著提高排序速度。希尔排序的时间复杂度依赖于所选的增量序列,最好的情况可以达到O(n log n),最坏情况则与所选增量序列有关,但通常优于O(n^2)。
再讲希尔排序之前,我们讲一下插入排序。
插入排序
插入排序(Insertion Sort)是一种简单直观的排序算法,适用于对小型数据集合或者基本有序的数据集合进行排序。它的核心思想是将一个记录(或数据元素)插入到已经排序好的有序表中,从而得到一个新的、记录数增加1的有序表。
插入排序的基本步骤如下:
- 初始化:假设数组的第一个元素已经被排序。
- 遍历数组:从第二个元素开始,每次取出一个元素(记为key),在已排序序列中从后向前扫描。
- 比较与移动:如果该元素(key)小于它前面的元素,则将前面的元素向后移动一位,为key腾出位置;否则,停止扫描。
- 插入元素:将key插入到已排序序列中的适当位置,即找到的正确位置或扫描停止的位置。
- 重复步骤2-4:对数组中的每个元素都执行这样的插入操作,直到数组完全排序。
插入排序的时间复杂度分析:
- 最好情况:当输入数组已经是排序状态时,插入排序只需要进行n-1次比较,不需要移动数据,时间复杂度为O(n)。
- 最坏情况:当输入数组是反序时,每次插入都相当于在数组的最前面插入,每次插入操作需要移动所有的已排序元素,时间复杂度为O(n^2)。
- 平均情况:对于随机数据,插入排序的时间复杂度也是O(n^2)。
插入排序的空间复杂度为O(1),因为它是一种原地排序算法,除了输入数组外,只需要常数级别的额外空间用于交换和临时存储。此外,插入排序是稳定的排序算法,即相等的元素的相对顺序不会改变。
画个图就是这样的:

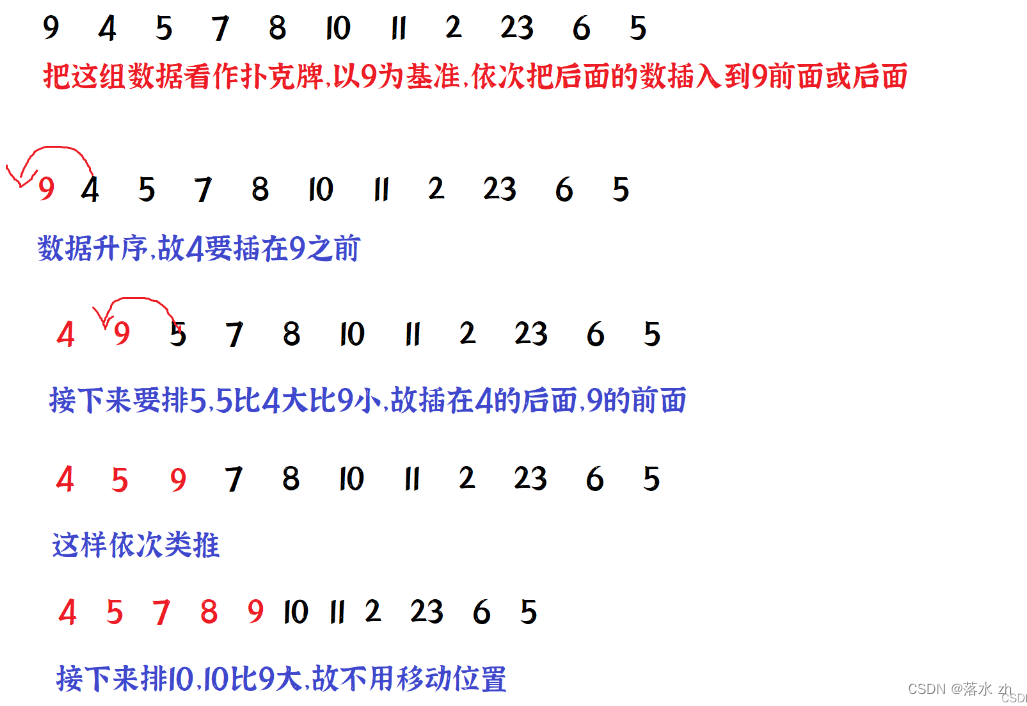

// 选择插入排序函数实现
void select_sort(int *array, int size)
{// 遍历整个数组,除了最后一个元素(因为它自然有序)for (int i = 0; i < size - 1; i++){// 选取当前位置i+1的元素作为待插入元素int temp = array[i + 1];// 初始化"已排序"部分的最后一个元素索引int end = i;// 当"已排序"部分的索引大于等于0时进入循环while (end >= 0){// 如果"已排序"部分的当前元素大于待插入元素if (array[end] > temp){// 将较大的元素向后移动一位,为待插入元素腾出空间std::swap(array[end + 1], array[end]);// 缩小"已排序"部分的范围,继续向前比较end--;}else{// 如果当前元素不大于待插入元素,说明找到了temp的正确位置// 或者已经检查到数组起始,此时无需再比较,直接跳出循环break;}}}// 循环结束,数组完成排序
}int main()
{int array[] = { 1,34,56,1,233,56,0 };for (auto e : array){std::cout << e << " ";}std::cout << std::endl;select_sort(array, sizeof(array) / sizeof(array[0]));for (auto e : array){std::cout << e << " ";}
}
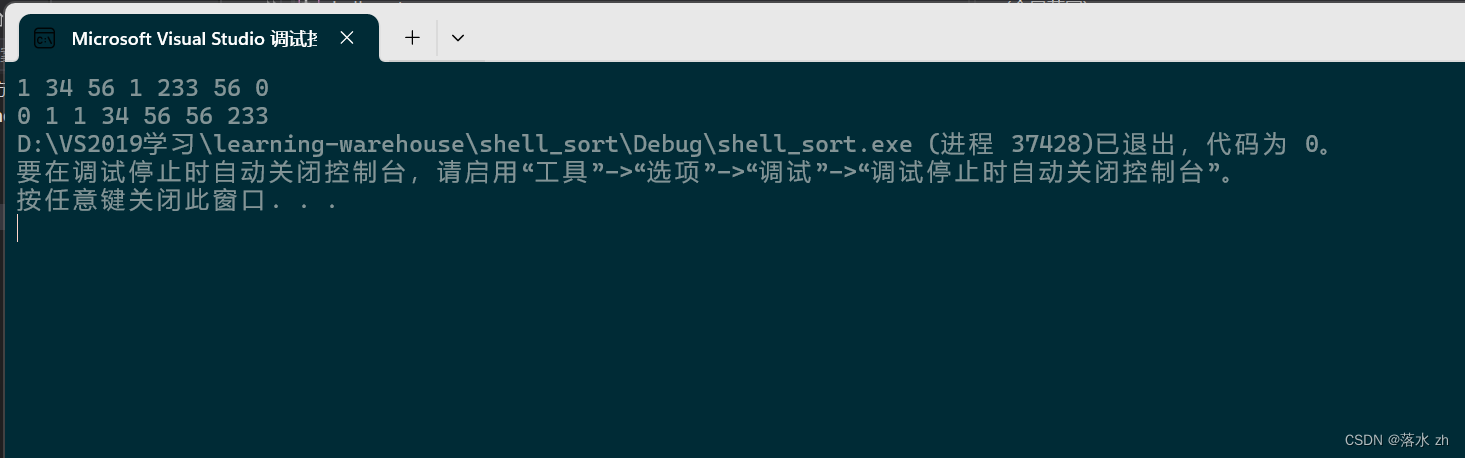
大家可以画个图,结合着图能比较清晰理解。
希尔排序
我们已经了解到了希尔排序的特殊形式直接插入排序,现在我们来了解一下更一般的形式=希尔排序。
我们之前用直接插入排序来让数据升序排列,我们来考虑一下它最糟糕的情况:数据是降序排序的。

这样的话,9之后的数据都要进行一次插入,插入到9之前,时间复杂度可以达到O(N2),但我们会遇到这样一种情况:

10比9大故不用进行插入了,而我们可不可以让这种情况更普遍一些呢?所以我们可以在进行排序之前,先进行一次预排序,让数据整体是升序的,这就是希尔排序。
希尔排序的步骤:
- 将数据分成gap组。
- 以gap为间隔进行直接插入排序。

//希尔排序
void ShellSort(int* a, int n)
{assert(a);int gap = 3;for (int i = 0; i < n - gap ; i+=gap){int end = i;int temp = a[end + gap];while (end >= 0){if (temp < a[end]){std::swap(array[end + gap], array[end]);end-=gap;}else{break;}}}
}这段代码的结果是什么样的呢?我们来画图看看:

其实我们只完成了一组红色数据的预排序,其实我们的预排序可以不止一组:
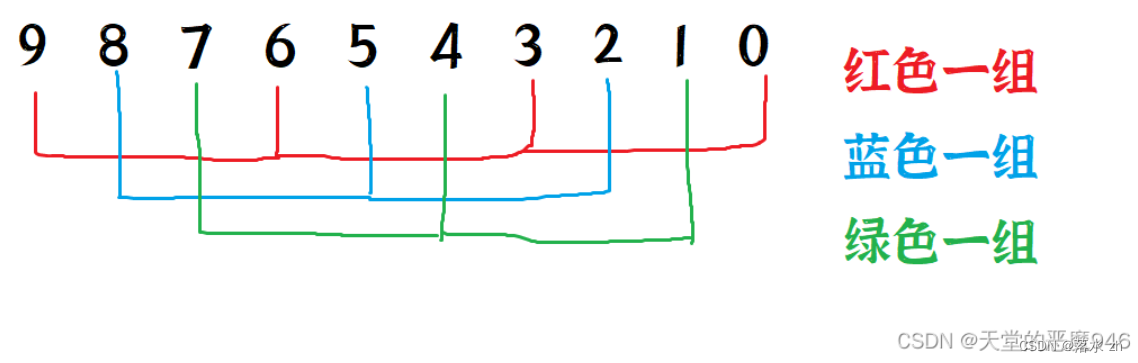
那么如何完成这三组的排序呢?很简单,加一层for循环。
//希尔排序
void shell_sort(int* array, int size)
{int gap = 3;for (int j = 0; j < 3; j++){for (int i = j; i < size - gap; i += gap){//后面一个待排元素int temp = array[i + gap];int end = i;while (end >= 0){if (array[end] > temp){std::swap(array[end + gap], array[end]);end-=gap;}else{break;}}}}}我们看看程序结果怎么样:
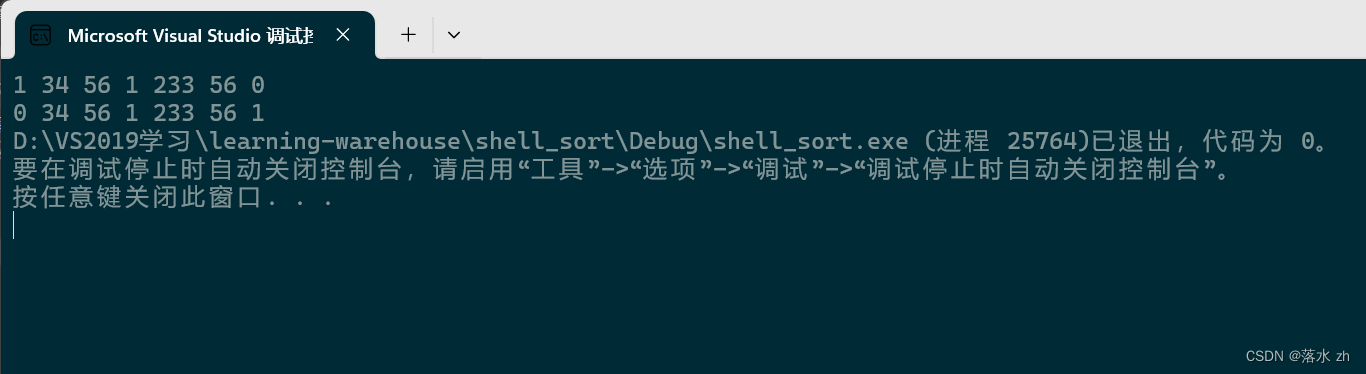
我们发现数据的排序是有一些变化,但好像还是有点混乱,这是因为gap的原因,这时候我们把gap改为2看看:
我们发现gap越大,数据排序越混乱,但移动的越快,**gap越小,数据越有序,但移动的越慢**这直接和时间复杂度有关。
// 希尔排序函数实现
void shell_sort(int* array, int size)
{// 初始化间隔(gap)为数组的长度int gap = size;// 当间隔大于1时,持续执行以下步骤,逐步减小间隔以达到排序效果while (gap > 1){// 计算新的间隔,这里使用的是一个简化的规则,将间隔除以3并加1,这是一种常用的递减策略gap = gap / 3 + 1;// 这个循环是为了处理不同子序列的起始位置,确保每个间隔下的元素都能被遍历到for (int j = 0; j < gap; j++){// 遍历数组,从当前子序列的起始位置开始,步长为当前的间隔for (int i = j; i < size - gap; i += gap){// 保存当前间隔位置的下一个元素,准备进行插入排序int temp = array[i + gap];int end = i;// 内部循环实现插入排序逻辑,将temp插入到已排序的子序列中正确的位置while (end >= 0){// 如果当前子序列中的元素大于temp,将该元素后移if (array[end] > temp){std::swap(array[end + gap], array[end]); // 交换元素end -= gap; // 移动到前一个位置继续比较}else{// 如果找到了temp的正确位置或已经比较到子序列的起始位置,跳出循环break;}}}}}// 当所有间隔遍历完成后,数组已经基本排序完成,由于最后一次gap为1,实质上进行了最后一次的插入排序收尾
}其实这段代码还有一个变形,也可以达到效果:多组并排
//希尔排序
void shell_sort(int* array, int size)
{int gap = size;while (gap > 1){gap = gap / 3 + 1;for (int i = 0; i < size - gap; i ++){//后面一个待排元素int temp = array[i + gap];int end = i;while (end >= 0){if (array[end] > temp){std::swap(array[end + gap], array[end]);end -= gap;}else{break;}}}}
}
递归版本
这里实现递归版本完全是为了锻炼思维,实际中不会这样写,仅供参考:
void select_sort(int* array, int size, int index)
{ // 如果index小于0,递归结束 if (index < 0) return; // 递归调用,先对前面的部分进行排序 select_sort(array, size, index - 1); // 如果index已经是最后一个元素(或者超过最后一个元素的索引),则不需要再进行排序 if (index >= size - 1) return; // 临时存储index+1位置的元素,这个元素可能是当前未排序部分的最小值 int temp = array[index + 1]; int end = index; // 从index位置开始向前比较 // 这是一个插入排序(Insertion Sort)的插入过程,但逻辑上不适合选择排序 while (end >= 0) { // 如果当前元素比temp大,则将当前元素后移 if (array[end] > temp) { std::swap(array[end], array[end + 1]); end--; } else { // 如果找到合适的位置,或者已经到达数组的开头,就跳出循环 break; } } }
希尔排序:
// 递归实现的插入排序,用于希尔排序中每轮的细分排序
void select_sort(int* array, int size, int index, int gap)
{// 递归基础情况:当索引小于0时,说明已处理完当前gap下的所有元素if (index < 0)return;// 递归调用,处理当前元素前一个gap位置的元素,逐步向前select_sort(array, size, index - gap, gap);// 防止数组越界,当索引达到size-gap时,说明当前gap下已无更多元素需要处理if (index >= size - gap)return;// 保存当前gap位置的元素值,准备进行插入排序int temp = array[index + gap];int end = index;// 插入排序逻辑,将temp插入到前方已排序的子序列中的正确位置while (end >= 0){if (array[end] > temp){// 交换元素,将较大的元素后移,为temp腾出位置std::swap(array[end + gap], array[end]);end -= gap; // 更新索引,继续向前比较}else{// temp已到达或超过其正确位置,停止循环break;}}
}// 实现希尔排序的主体函数,使用递归的select_sort进行每一轮的细分排序
void shell_sort(int* array, int size, int index)
{int gap = size;// 循环直到gap减至1,每轮使用一个较小的gap进行插入排序while (gap > 1){ // 计算下一轮的gap值,这里采用gap = gap / 3 + 1是一种常见但非唯一的策略gap = gap / 3 + 1;// 使用当前gap值调用select_sort进行插入排序select_sort(array, size, index, gap);}
}相关文章:

十大排序 —— 希尔排序
十大排序 —— 希尔排序 什么是希尔排序插入排序希尔排序递归版本 我们今天来看另一个很有名的排序——希尔排序 什么是希尔排序 希尔排序(Shell Sort)是插入排序的一种更高效的改进版本,由Donald Shell于1959年提出。它通过比较相距一定间…...
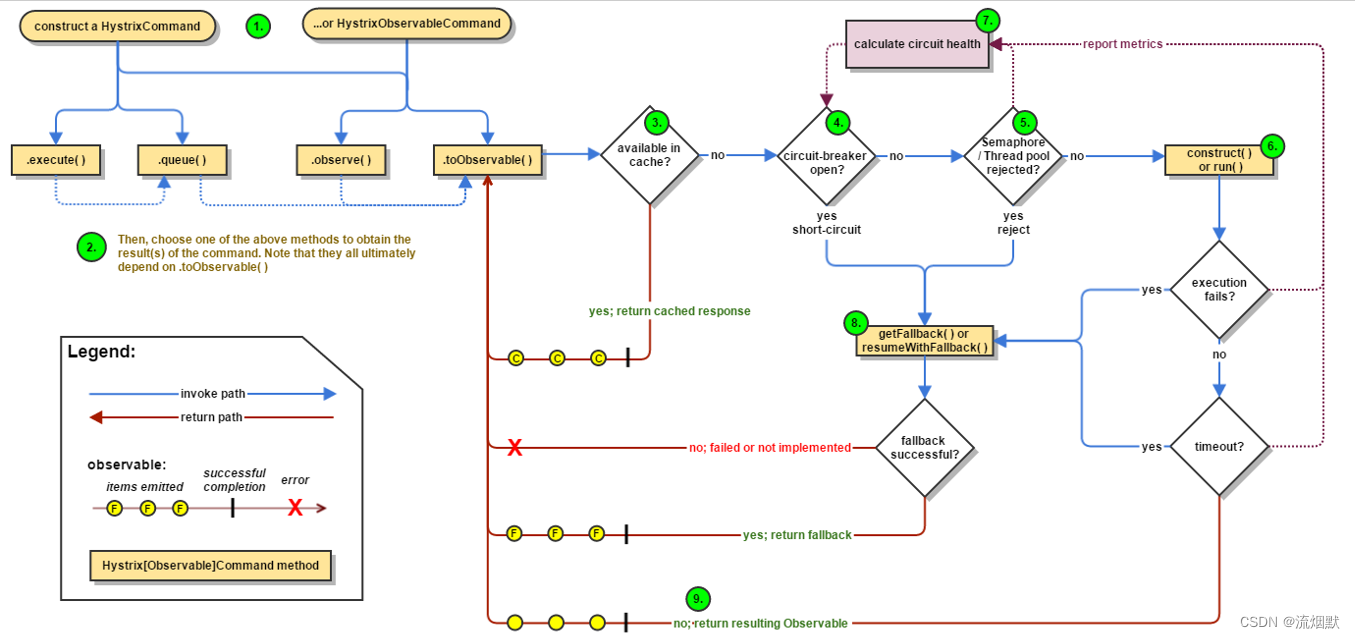
SpringCloud Hystrix服务熔断实例总结
SpringCloud Hystrix断路器-服务熔断与降级和HystrixDashboard SpringCloud Hystrix服务降级实例总结 本文采用版本为Hoxton.SR1系列,SpringBoot为2.2.2.RELEASE <dependency><groupId>org.springframework.cloud</groupId><artifactId>s…...
为什么没有输出九九乘法表?
下面的程序本来想输出九九乘法表到屏幕上,为什么没有输出呢?怎样修改? <!DOCTYPE html> <html> <head> <meta charset"utf-8" /> <title>我的HTML练习</title> …...

EasyRecovery5步轻松恢复电脑手机数据,EasyRecovery带你探索!
在当今的数字化时代,数据已经成为我们生活和工作中不可或缺的一部分。无论是个人照片、工作文件还是重要的商业信息,数据的安全存储和恢复都显得尤为重要。EasyRecovery作为一款广受欢迎的数据恢复软件,为用户提供了强大的数据恢复功能&#…...

904. 水果成篮
904. 水果成篮 原题链接:完成情况:解题思路:参考代码:_904水果成篮_滑动窗口 错误经验吸取 原题链接: 904. 水果成篮 https://leetcode.cn/problems/fruit-into-baskets/description/ 完成情况: 解题思…...

在618集中上新,蕉下、VVC们为何押注拼多多?
编辑|Ray 自前两年崛起的防晒产品,今年依旧热度不减。 头部品牌蕉下,2020年入驻拼多多,如今年销售额已过亿元。而自去年起重点押注拼多多的时尚防晒品牌VVC,很快销量翻番。这两家公司,不约而同在618之前上…...

Maximo Attachments配置
以下内容以 Windows 上 Maximo 为例,并假定设置 DOCLINKS 的根路径为 “C:\DOCLINKS”。 HTTP Server配置 修改C:\Program Files\IBM\HTTPServer\conf\httpd.conf文件 查找 “DocumentRoot” 并修改成如下配置 DocumentRoot "C:\DOCLINKS"查找 “<…...

一分钟了解香港的场外期权报价
香港的场外期权报价 在香港这个国际金融中心,场外期权交易是金融市场不可或缺的一部分。场外期权,作为一种非标准化的金融衍生品,为投资者提供了在特定时间以约定价格买入或卖出某种资产的机会。对于希望参与这一市场的投资者来说࿰…...

专业开放式耳机什么牌子更好?六大技巧教你不踩坑!
相信很多入坑的朋友再最开始挑选耳机的时候都会矛盾,现在市面上这么多耳机,我该怎么选择?其实对于开放式耳机,大家都没有一个明确的概念,可能会为了音质的一小点提升而耗费大量的资金,毕竟这是一个无底洞。…...

注意!!24软考系统集成有变化,第三版考试一定要看这个!
系统集成在今年年初改版之后,上半年的考试也取消了,留给大家充足的时间来学习新的教材和考纲。但11月也将是第三版考纲的第1次考试,重点到底有什么?今天带大家详细的了解一下最新版中项考试大纲。 一、考试说明 1.考试目标 通过…...
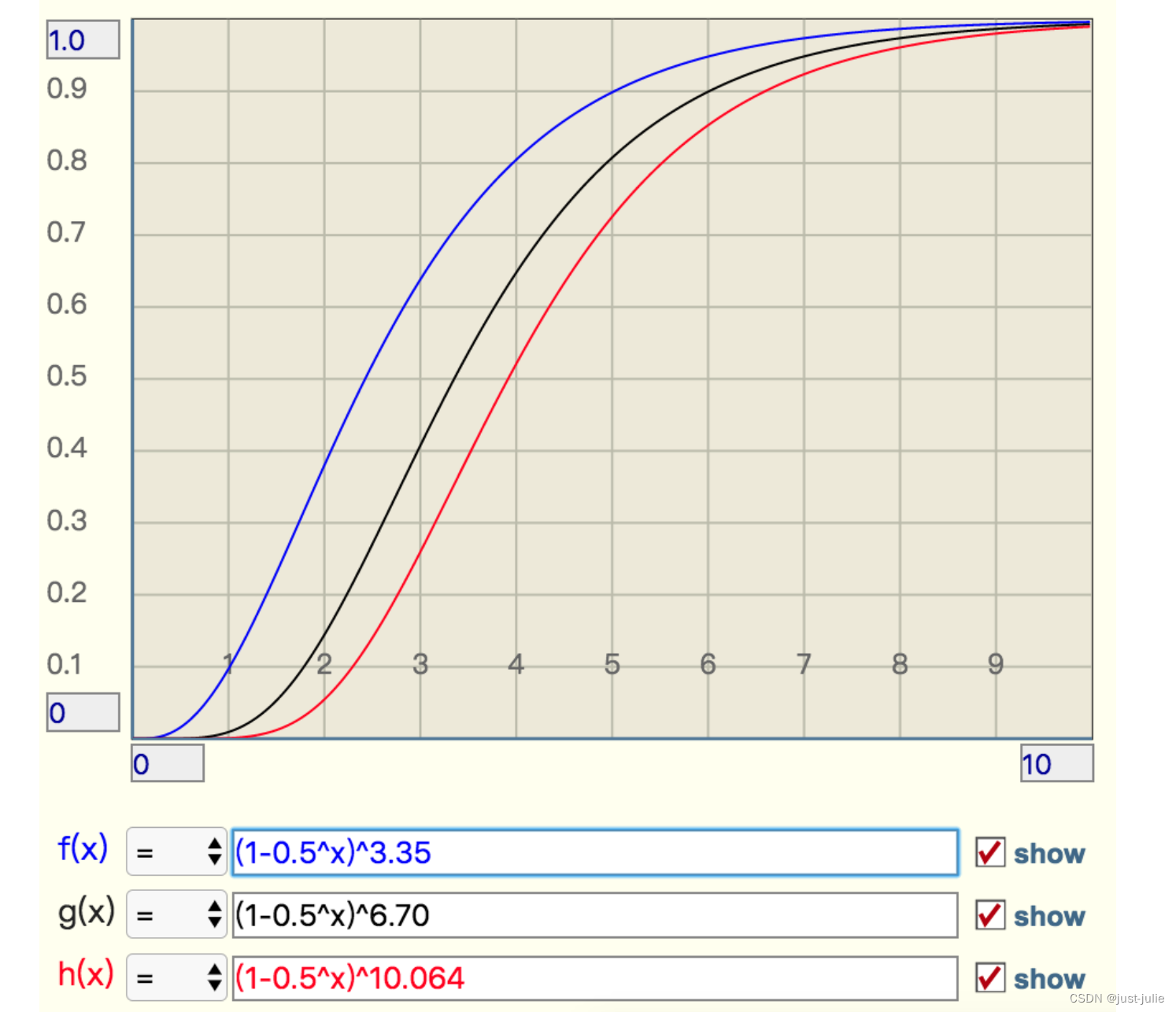
Redis数据结构HyperLogLog以及布隆过滤器
HyperLogLog 引言 在开始之前,先思考一个常见的业务问题:如果负责开发维护一个大型的网站,有一天老板找产品经理要网站每个网页每天的UV数据,然后来开发这个统计模块,需要如何实现? 如果统计PV非常好办&…...
C++——从C语言快速入门
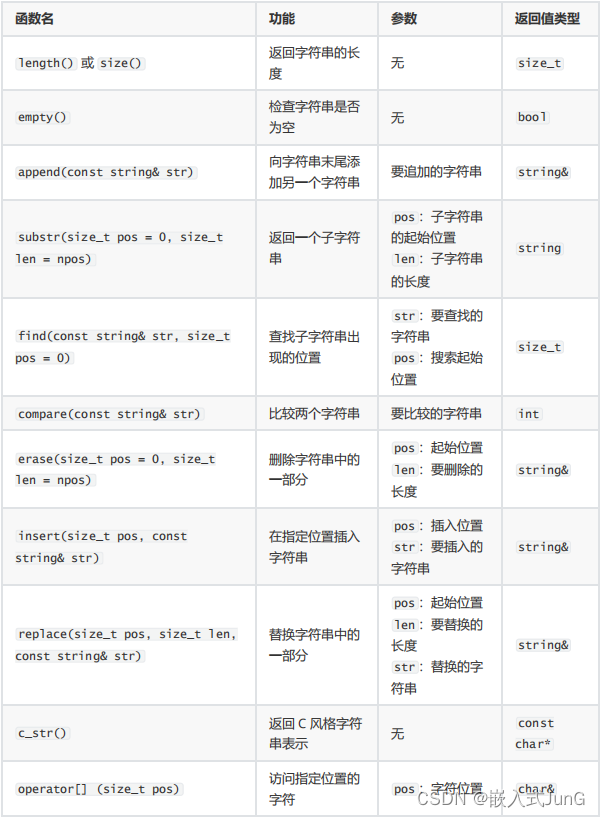
目录 一、数组 1、声明数组 2、初始化数组 3、访问数组元素 4、示例 5、注意事项 6、数组小练习 计算器支持加减乘除 数组找最大值 二、指针 三、字符串 string 类型 一、数组 在 C 中,数组是一种存储固定大小的相同类型元素的序列。数组的所有元素都存…...

thinkpad T440p ubuntu-slam软件安装记录
安装问题 1.ubuntu20.04安装后提示"x86/cpu:VMX(outside TXT) disabled by BIOS" 这是虚拟化被禁止了,到BIOS里去把Virtualization选项打开即可。 2.ACPI Error:Needed type[Reference],found [Integer] 等错误 link这篇博客中提到该问题,…...
本地电脑访问windows server系统服务器 并传输文件
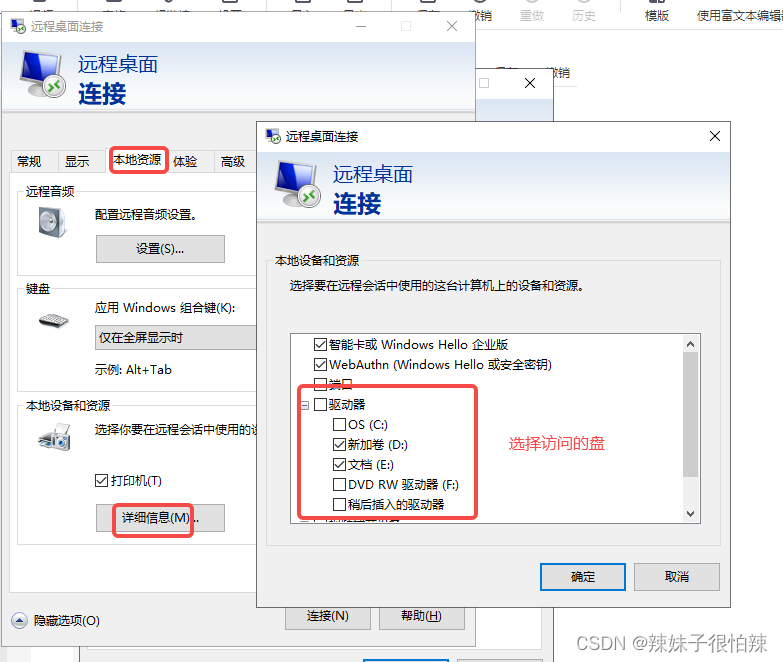
1、 mstsc 命令打开远程桌面连接。 2、填入登入的用户密码,在本地资源中设置需要共享的盘。登入成功后就可以在服务器与本地电脑互传文件了。...
kubernetes负载均衡---MetalLB
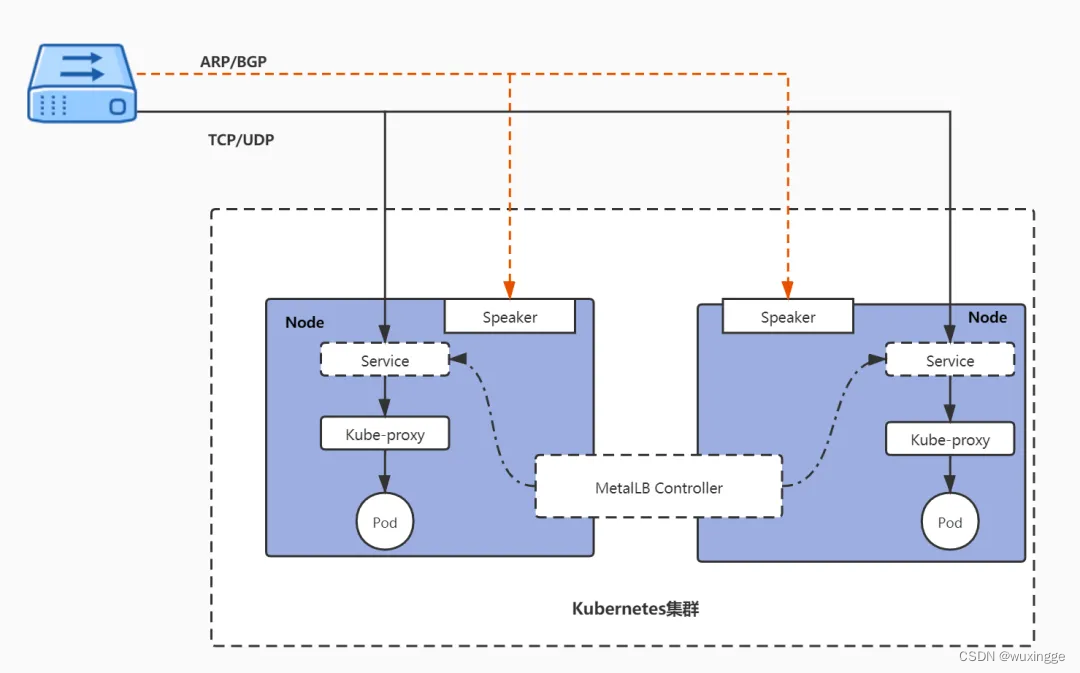
https://github.com/metallb/metallb 参考 : https://mp.weixin.qq.com/s/MBOWfcTjFMmgJFWw-FIk0Q 自建的Kubernetes集群,默认情况下是不支持负载均衡的。当需要提供服务的外部访问时,可使用 Ingress、NodePort等方式。他们都存在一些问题 …...
)
Python面试宝典:Python中与设计模式相关的面试笔试题(1000加面试笔试题助你轻松捕获大厂Offer)
Python面试宝典:1000加python面试题助你轻松捕获大厂Offer【第二部分:Python高级特性:第二十二章:代码设计和设计模式:第二节:设计模式】 第二十二章:代码设计和设计模式第二节:设计模式创建型模式结构型模式行为型模式python中与设计模式相关的面试笔试题面试题1面试题…...
以sqlilabs靶场为例,讲解SQL注入攻击原理【18-24关】
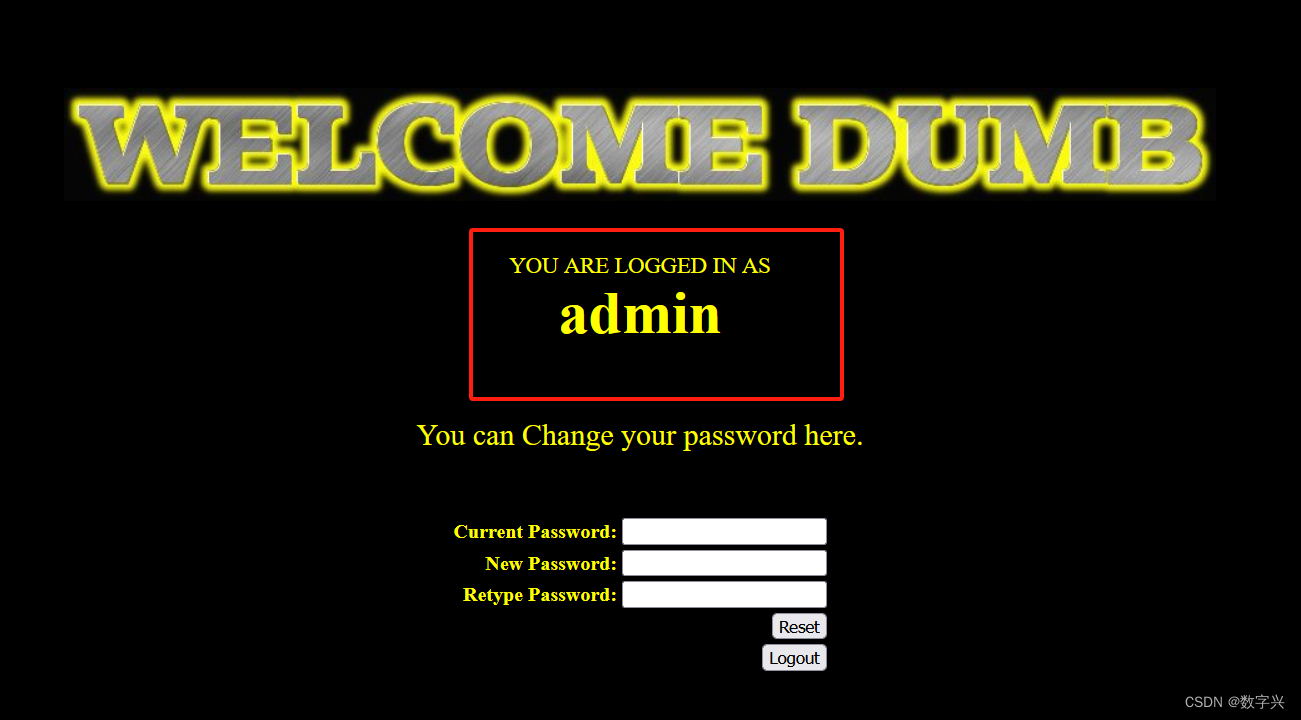
【less-18】 打开时,获取了自己的IP地址。,通过分析源码知道,会将用户的user-agent作为参数记录到数据库中。 提交的是信息有user-Agent、IP、uname信息。 此时可以借助Burp Suite 工具,修改user_agent,实现sql注入。…...
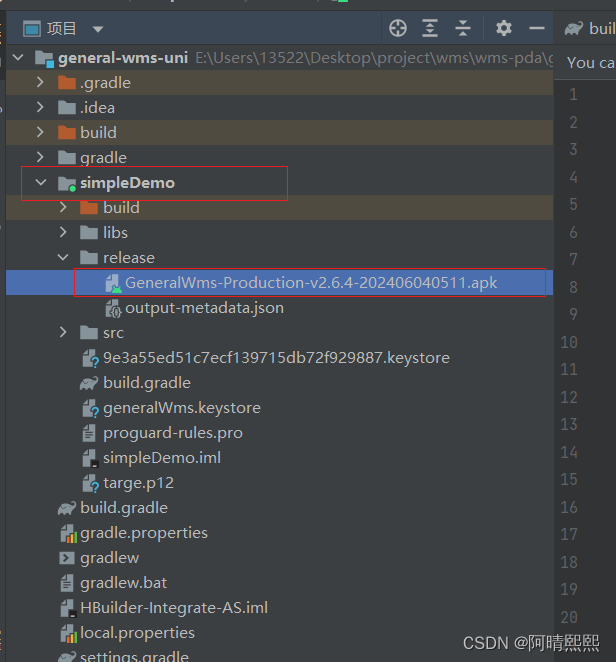
【已有项目版】uniapp项目发版pda -- Android Studio
必备资料清单: 构建完成的app项目 在HBuilderX开发的uniapp项目 .keystore文件 文章目录 1. 安装Android Studio:https://developer.android.google.cn/studio?hlzh-cn2. 安装Android 离线SDK:https://nativesupport.dcloud.net.cn/AppDocs…...

三维重建,谁才是顶流?
3DGS技术是近年来计算机视觉领域最具突破性的研究成果之一。它不仅在学术界引起了广泛关注,成为计算机视觉、SLAM等领域的研究热点,而且每天都有大量基于Gaussian Splatting的新研究问世。此外,3DGS技术在商业应用方面也取得了显著进展&#…...
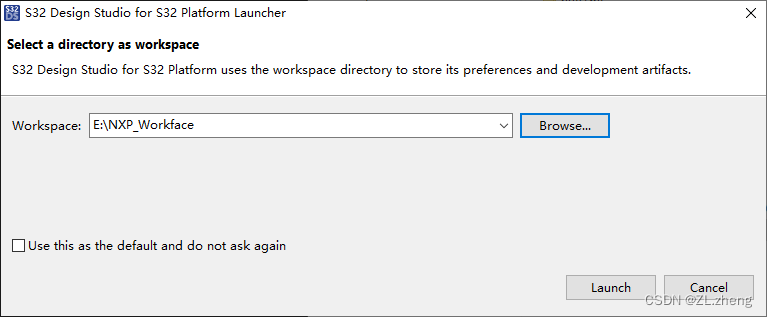
s32k314【入门新手篇】-开发环境安装【ds32开发平台】
软件包下载 登录nxp官网下载:https://www.nxp.com/ 然后输入关键字:S32 查看 下载安装包 以上三步请先注册好并登录你的个人账号 下载完之后如下: 软件安装 eb安装并激活【试用版】 激活 2 安装ds 弹出什么就安装什么就好了。 …...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...
