二叉树讲解
目录
前言
二叉树的遍历
层序遍历
队列的代码
queuepush和queuepushbujia的区别
判断二叉树是否是完全二叉树
前序
中序
后序
功能展示
创建二叉树
初始化
销毁
简易功能介绍
二叉树节点个数
二叉树叶子节点个数
二叉树第k层节点个数
二叉树查找值为x的节点
判断是否为单值二叉数
判断二叉数高度
前言
本文讲解关于二叉树的创建和各种功能的实现,重点讲解前,中,后和层序遍历的写法
(层序遍历放到了本文前面先讲,如果是刚接触二叉数可以先看功能展示)
前中后序的遍历都用到了递归都写法
而层序遍历却不方便,只能创建队列来解决
二叉树的遍历
层序遍历
层序遍历这里重点讲解一下
因为不能使用递归,只好创建队列来帮助实现
队列的代码
头文件
typedef BTNode* QDataType;typedef struct QueueNode
{struct QueueNode* next;QDataType val;
}QNode;typedef struct Queue
{QNode* phead;QNode* ptail;int size;
}Queue;void QueueInit(Queue* pq);
void QueueDestroy(Queue* pq);// 队尾插入
void QueuePush(Queue* pq, QDataType x);
void QueuePushbujia(Queue* pq, QDataType x);
// 队头删除
void QueuePop(Queue* pq);// 取队头和队尾的数据
QDataType QueueFront(Queue* pq);
QDataType QueueBack(Queue* pq);int QueueSize(Queue* pq);
bool QueueEmpty(Queue* pq);源码
void QueueInit(Queue* pq)
{assert(pq);pq->phead = NULL;pq->ptail = NULL;pq->size = 0;
}void QueueDestroy(Queue* pq)
{assert(pq);QNode* cur = pq->phead;while (cur){QNode* next = cur->next;free(cur);cur = next;}pq->phead = pq->ptail = NULL;pq->size = 0;
}// 队尾插入
void QueuePush(Queue* pq, QDataType x)
{assert(pq);QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode == NULL){perror("malloc fail");return;}newnode->next = NULL;newnode->val = x;if (pq->ptail == NULL){pq->phead = pq->ptail = newnode;}else{pq->ptail->next = newnode;pq->ptail = newnode;}pq->size++;
}void QueuePushbujia(Queue* pq, QDataType x)
{assert(pq);QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode == NULL){perror("malloc fail");return;}newnode->next = NULL;newnode->val = x;if (pq->ptail == NULL){pq->phead = pq->ptail = newnode;}else{pq->ptail->next = newnode;pq->ptail = newnode;}
}
// 队头删除
void QueuePop(Queue* pq)
{assert(pq);assert(pq->size != 0);/*QNode* next = pq->phead->next;free(pq->phead);pq->phead = next;if (pq->phead == NULL)pq->ptail = NULL;*/// 一个节点if (pq->phead->next == NULL){free(pq->phead);pq->phead = pq->ptail = NULL;}else // 多个节点{QNode* next = pq->phead->next;free(pq->phead);pq->phead = next;}pq->size--;
}QDataType QueueFront(Queue* pq)
{assert(pq);assert(pq->phead);return pq->phead->val;
}QDataType QueueBack(Queue* pq)
{assert(pq);assert(pq->ptail);return pq->ptail->val;
}int QueueSize(Queue* pq)
{assert(pq);return pq->size;
}bool QueueEmpty(Queue* pq)
{assert(pq);return pq->size == 0;
}
queuepush和queuepushbujia的区别
两个都是将数据尾插进去,但bujia函数并不会对size加加
这样我们不仅可以正常打印N还不影响真实数据的打印
void BinaryTreeLevelOrder(BTNode* root)
{assert(root);Queue a;QueueInit(&a);BTNode* n = BuyNode1(root->_data);n = root;BTNode* null = BuyNode1('N');printf("%c ", n->_data);while (1){if (n->_left != NULL){QueuePush(&a, n->_left);}else{QueuePushbujia(&a,null);}if (n->_right != NULL){QueuePush(&a, n->_right);}else{QueuePushbujia(&a,null);}if (QueueEmpty(&a)){break;}n = QueueFront(&a);QueuePop(&a);if (n->_data == 'N'){a.size++;}printf("%c ", n->_data);}
}每拿出一个头数据时就会对size--这样的话如果为N的话很有可能会出现size减完了但实际数据没有打印完的情况
所以这里加入了判断n->_data等于N时应该让size++
利用写出来的层序遍历就可以实现
判断二叉树是否是完全二叉树
i和x的作用
如果是完全二叉树遇到一个N后不可能再遇到N意外的数了
否则就是非完全二叉树
利用这一特征
当遇到第一个N时让i++
如果i不等于0说明遇到过N了如果此时遇到了非N的数那么就让n++
如果两个数同时不为0则为非完全二叉树
int BinaryTreeComplete(BTNode* root)
{assert(root);Queue a;QueueInit(&a);BTNode* n = BuyNode1(root->_data);n = root;BTNode* null = BuyNode1('N');//printf("%c ", n->_data);char pan = 'x';int i = 0;int x = 0;while (1){if (n->_left != NULL){QueuePush(&a, n->_left);}else{QueuePushbujia(&a, null);}if (n->_right != NULL){QueuePush(&a, n->_right);}else{QueuePushbujia(&a, null);}if (QueueEmpty(&a)){break;}n = QueueFront(&a);QueuePop(&a);if (n->_data == 'N'){a.size++;}//printf("%c ", n->_data);pan = n->_data;if (pan == 'N'){i++;}if (i !=0){if (pan != 'N'){x++;}}if (i!=0&&x!=0){return 1;}}return 0;
}前序
void BinaryTreePrevOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}printf("%c ", root->_data);BinaryTreePrevOrder(root->_left);BinaryTreePrevOrder(root->_right);
}中序
void BinaryTreeInOrder(BTNode* root)
{if (root == NULL){printf("N");return;}BinaryTreeInOrder(root->_left);printf("%c ", root->_data);BinaryTreeInOrder(root->_right);
}后序
void BinaryTreePostOrder(BTNode* root)
{if (root == NULL){printf("N");return;}BinaryTreePostOrder(root->_left);BinaryTreePostOrder(root->_right);printf("%c ", root->_data);
}功能展示
完成关于二叉树的如下功能
//初始化
BTNode* BuyNode1(BTDataType x);// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);
// 二叉树销毁
void BinaryTreeDestory(BTNode** root);
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root);
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root);
// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root);
//判断是否为单值二叉数
bool isUnivalTree(struct BTNode* root);
//判断二叉数高度
int maxDepth(struct BTNode* root);创建二叉树
手动创建一个二叉树可以让后面的功能更方便调试
首先确定结构体内容如下
typedef char BTDataType;typedef struct BinaryTreeNode
{BTDataType _data;struct BinaryTreeNode* _left;struct BinaryTreeNode* _right;
}BTNode;在进行手动创建一个二叉树
创建之前需要初始化结构体
初始化
//初始化
BTNode* BuyNode1(BTDataType x)
{BTNode* n = (BTNode*)malloc(sizeof(BTNode));if (n == NULL){perror("malloc false");return NULL;}n->_data = x;n->_left = NULL;n->_right = NULL;return n;
}有了初始化代码就可以正式创建二叉树了
BTNode* headadd()
{BTNode* a1 = BuyNode1('a');BTNode* a2 = BuyNode1('b');BTNode* a3 = BuyNode1('c');BTNode* a4 = BuyNode1('d');BTNode* a5 = BuyNode1('e');a1->_left = a2;a1->_right = a3;a2->_left = a4;a4->_right = a5;return a1;
}此时二叉树就建好了
有了初始化就需要有销毁,防止内存泄漏
销毁
使用递归思想比较方便
void BinaryTreeDestory(BTNode** root)
{assert(root);assert(*root);BinaryTreeDestory(&((*root)->_left));BinaryTreeDestory(&((*root)->_right));free(*root);*root == NULL;
}简易功能介绍
大多数采用递归的方法即可轻松解决
二叉树节点个数
int BinaryTreeSize(BTNode* root)
{if (root == NULL){return 0;}return 1+BinaryTreeSize(root->_left)+BinaryTreeSize(root->_right);二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->_left == NULL && root->_right == NULL){return 1;}return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{if (root == NULL||k<1){return 0;}if (root!=NULL&&k == 1){return 1;}return BinaryTreeLevelKSize(root->_left, k - 1) +BinaryTreeLevelKSize(root->_right, k - 1);
}二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL){return NULL;}if (root->_data == x){return root;}BTNode* lf = BinaryTreeFind(root->_left, x);if (lf != NULL){return lf;}BTNode* lr = BinaryTreeFind(root->_right, x);if (lr != NULL){return lr;}return NULL;
}判断是否为单值二叉数
bool isUnivalTree(BTNode* root)
{if (root == NULL){return true;}if (root->_left){if (root->_data!= root->_left->_data){return false;}}if (!isUnivalTree(root->_left)){return false;}if (root->_right){if (root->_data != root->_right->_data){return false;}}if (!isUnivalTree(root->_right)){return false;}return true;
}判断二叉数高度
int maxDepth(BTNode* root)
{if (root == NULL){return 0;}int leftsize = maxDepth(root->_left);int rightsize = maxDepth(root->_right);return leftsize > rightsize ? leftsize + 1 : rightsize + 1;
}相关文章:

二叉树讲解
目录 前言 二叉树的遍历 层序遍历 队列的代码 queuepush和queuepushbujia的区别 判断二叉树是否是完全二叉树 前序 中序 后序 功能展示 创建二叉树 初始化 销毁 简易功能介绍 二叉树节点个数 二叉树叶子节点个数 二叉树第k层节点个数 二叉树查找值为x的节点 判…...
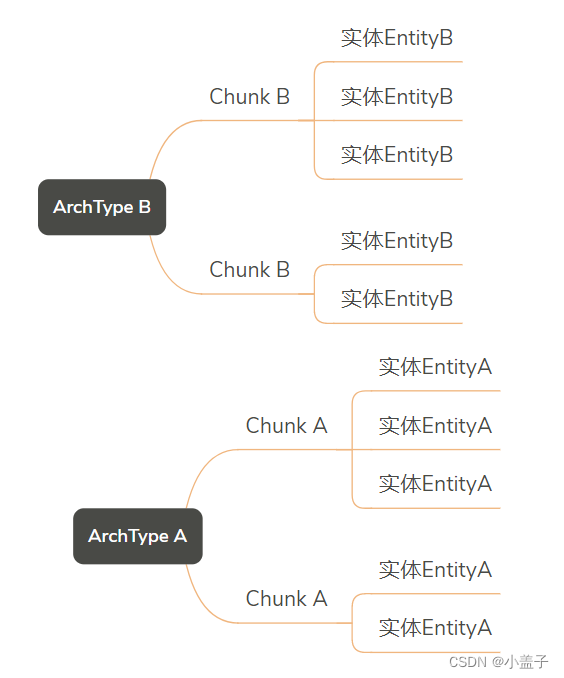
Unity DOTS技术(五)Archetype,Chunk,NativeArray
文章目录 一.Chunk和Archetype什么是Chunk?什么是ArchType 二.Archetype创建1.创建实体2.创建并添加组件3.批量创建 三.多线程数组NativeArray 本次介绍的内容如下: 一.Chunk和Archetype 什么是Chunk? Chunk是一个空间,ECS系统会将相同类型的实体放在Chunk中.当一个Chunk…...

算法学习笔记(7.1)-贪心算法(分数背包问题)
##问题描述 给定 𝑛 个物品,第 𝑖 个物品的重量为 𝑤𝑔𝑡[𝑖−1]、价值为 𝑣𝑎𝑙[𝑖−1] ,和一个容量为 𝑐𝑎&…...

气膜建筑的施工对周边环境影响大吗?—轻空间
随着城市化进程的加快,建筑行业的快速发展也带来了环境问题。噪音、灰尘和建筑废料等对周边居民生活和生态环境造成了不小的影响。因此,选择一种环保高效的施工方式变得尤为重要。气膜建筑作为一种新兴的建筑形式,其施工过程对周边环境的影响…...

【计算机网络】对应用层HTTP协议的重点知识的总结
˃͈꒵˂͈꒱ write in front ꒰˃͈꒵˂͈꒱ ʕ̯•͡˔•̯᷅ʔ大家好,我是xiaoxie.希望你看完之后,有不足之处请多多谅解,让我们一起共同进步૮₍❀ᴗ͈ . ᴗ͈ აxiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客 本文由xiaoxieʕ̯•͡˔•̯᷅ʔ 原创 CSDN 如…...

30分钟快速入门TCPDump
TCPDump是一款功能强大的网络分析工具,它可以帮助网络管理员捕获并分析流经网络接口的数据包。由于其在命令行环境中的高效性与灵活性,TCPDump成为了网络诊断与安全分析中不可或缺的工具。本文将详细介绍TCPDump的基本用法,并提供一些高级技巧…...

Python | 刷题日记
1.海伦公式求三角形的面积 area根号下(p(p-a)(p-b)(p-c)) p是周长的一半 2.随机生成一个整数 import random xrandom.randint(0,9)#随机生成0到9之间的一个数 yeval(input("please input:")) if xy:print("bingo") elif x<y:pri…...
“JS逆向 | Python爬虫 | 动态cookie如何破~”
案例目标 目标网址:aHR0cHMlM0EvL21hdGNoLnl1YW5yZW54dWUuY29tL21hdGNoLzI= 本题目标:提取全部 5 页发布日热度的值,计算所有值的加和,并提交答案 常规 JavaScript 逆向思路 JavaScript 逆向工程通常分为以下三步: 寻找入口:逆向工程的核心在于找出加密参数的生成方式。…...
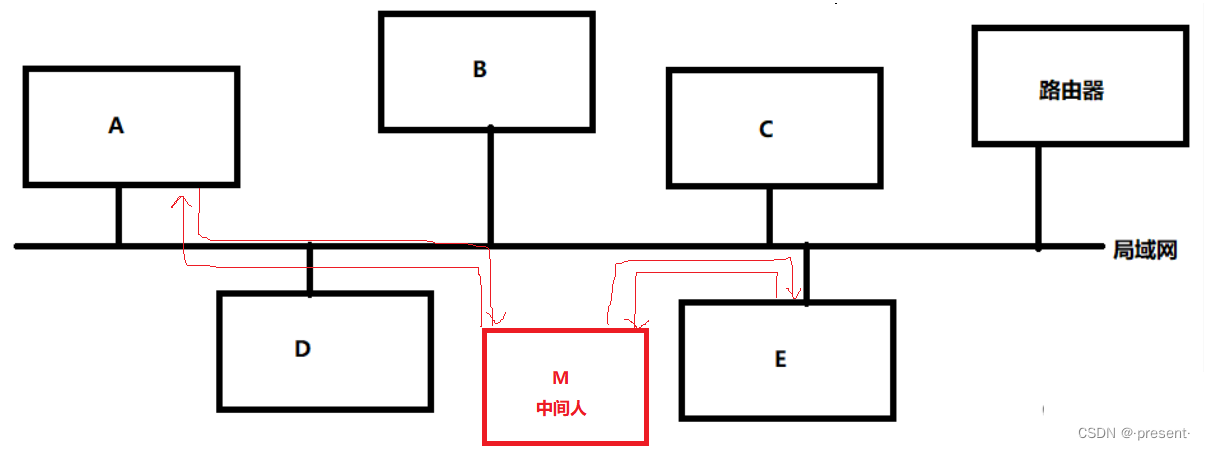
十.数据链路层——MAC/ARP
IP和数据链路层之间的关系 引言 在IP一节中,我们说IP层路由(数据转发)的过程,就像我们跳一跳游戏一样,从一个节点,转发到另一个节点 它提供了一种将数据从A主机跨网络发到B主机的能力 什么叫做跨网络??&a…...

Linux主机安全可视化运维(免费方案)
本文介绍如何使用免费的主机安全软件,在自有机房或企业网络实现对Linux系统进行可视化“主机安全”管理。 一、适用对象 本文适用于个人或企业内的Linux服务器运维场景,实现免费、高效、可视化的主机安全管理。提前发现主机存在的安全风险,全方位实时监控主机运行时入侵事…...

Vite + Vue 3 前端项目实战
一、项目创建 npm install -g create-vite #安装 Vite 项目的脚手架工具 # 或者使用yarn yarn global add create-vite#创建vite项目 create-vite my-vite-project二、常用Vue项目依赖安装 npm install unplugin-auto-import unplugin-vue-components[1] 安装按需自动导入组…...

python-字符替换
[题目描述] 给出一个字符串 s 和 q 次操作,每次操作将 s 中的某一个字符a全部替换成字符b,输出 q 次操作后的字符串输入 输入共 q2 行 第一行一个字符串 s 第二行一个正整数 q,表示操作次数 之后 q 行每行“a b”表示把 s 中所有的a替换成b输…...
团队项目开发使用git工作流(IDEA)【精细】
目录 开发项目总体使用git流程 图解流程 1.创建项目仓库[组长完成] 2. 创建项目,并进行绑定远程仓库【组长完成】 3.将项目与远程仓库(gitee)进行绑定 3.1 创建本地的git仓库 3.2 将项目添加到缓存区 3.3 将项目提交到本地仓库&#…...

爬虫案例实战
文章目录 一、窗口切换实战二、京东数据抓取 一、窗口切换实战 案例实战:使用selenium实现打开百度和腾讯两个窗口并切换 知识点:用到selenium中execute_script()执行js代码及switch_to.window()方法 全部代码如下: import time import war…...
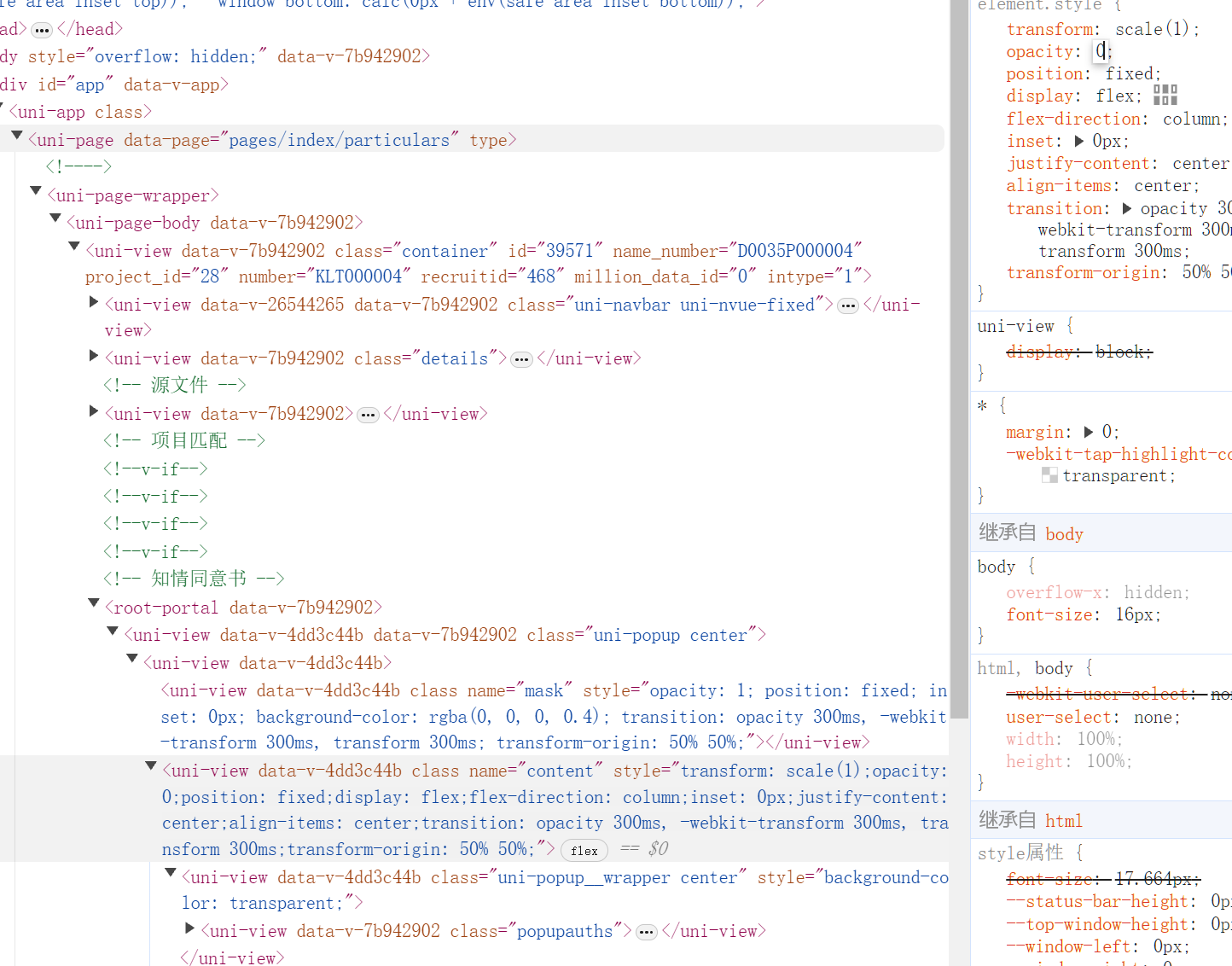
uniapp uni-popup内容被隐藏问题
今天开发新需求的时候发现uni-popup 过一会就被隐藏掉只留下遮罩(css被更改了),作者进行了如下调试。 1.讲uni-popup放入其他节点内 失败! 2.在生成dom后在打开 失败! 3.uni-popup将该节点在包裹一层 然后将统计设置样式,v-if v-s…...
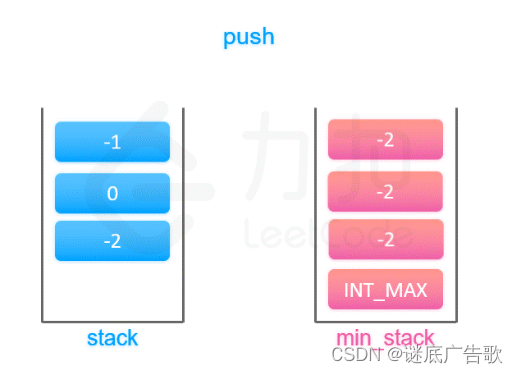
leetcode155 最小栈
题目 设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。 实现 MinStack 类: MinStack() 初始化堆栈对象。void push(int val) 将元素val推入堆栈。void pop() 删除堆栈顶部的元素。int top() 获取堆栈顶部的元素。i…...
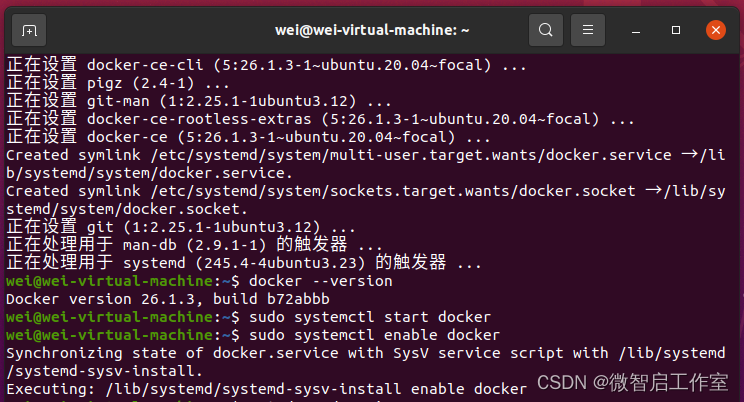
在Ubuntu乌班图上安装Docker
最近在学习乌班图相关的内容,找了一些文档安装的都是报错的,于是记录一下学习过程,希望也能帮助有缘人,首先查看乌班图的系统版本,我的是如下的: cat /proc/version以下是在Ubuntu 20.04版本上安装Docker。…...

【Redis数据库百万字详解】数据持久化
文章目录 一、持久化1.1、什么是持久化1.2、持久化方式1.3、RDB优缺点1.4、AOF优缺点 二、RDB持久化触发机制2.1、手动触发2.2、自动触发 三、RDB持久化配置3.1、配置文件3.2、配置查询/设置3.3、禁用持久化3.4、RDB文件恢复 四、RDB持久化案例4.1、手动持久化4.2、自动持久化案…...
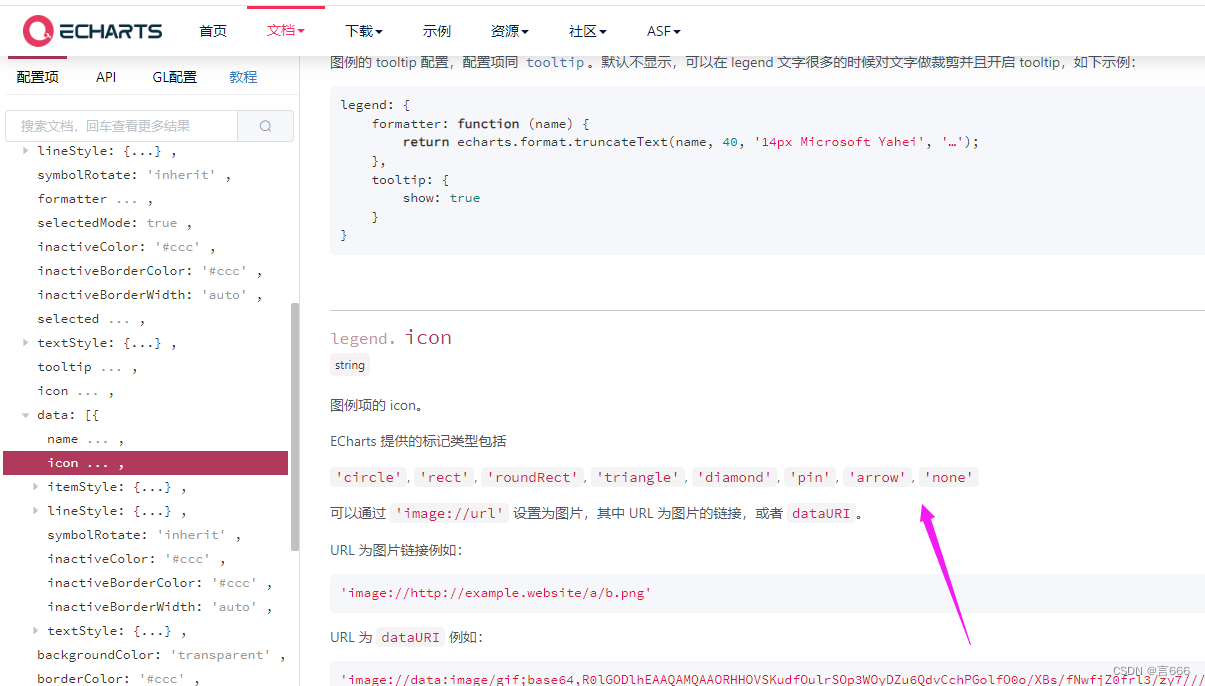
echarts legend. icon的展示
默认展示 icon展示circle圆形rect矩形roundRect圆角矩形triangle三角形diamond菱形pin水滴arrow箭头none不显示...

PHPstudy情况下上传图片马需要的.htaccess文件
网上的方法是无效的: <FilesMatch "test.jpg">SetHandler application/x-httpd-php</FilesMatch>原因是新版本的phpstudy使用了cgi模式,而网上的方法只适用于linux模式。 <FilesMatch "tpm.png"> AddHandler fcgid-script …...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...
