刷题记录(20240605)
1.数组构造
题目描述
小红的数组构造小红希望你构造一个数组满足以下条件:
1.数组共有 n个元素,且所有元素两两不相等。
2.所有元素的最大公约数等于 k。
3.所有元素之和尽可能小。请你输出数组元素之和的最小值。
输入描述:
两个正整数 n 和 k。
输出描述:
一个正整数,代表数组元素之和的最小值,
输入示例:
3 1
输出示例:6
分析:
数组只能是 1k,2k,3k,……,(n-1)k,nk
求和可以用等差数列求和公式 (n+1)nk/2
代码:
#include <iostream>
using namespace std;int main() {long long result = 0;int n, k;cin >> n >> k;// 使用等差数列求和公式进行计算result = k * (n * (n + 1LL) / 2);cout << result << endl;return 0;
}2.精华帖子
题目描述
小红书的推荐帖子列表为 [0,n),其中所有的帖子初始状态为"普通",现在运营同学把其中的一些帖子区间标记为了“精华"。
运营同学选择了固定长度 k,对整个帖子列表截取,要求计算在固定的截取长度k下,能够截取获得的最多精华帖子数量。
输入描述
第一行输入三个正整数 n,m,k,分别代表初始帖子列表长度,精华区间的数量,以及运营同学准备截取的长度。
接下来的 m 行,每行输入两个正整数,| 和r,代表第i个左闭右开区间。
1 <= k<=n<= 20000000.
1<= m <= 100000.
0 <=l<ri<= n,保证任意两个区间是不重复的。
输出描述
一个正整数,代表截取获得的最多的精华帖子数量。
输入示例
5 2 3
1 2
3 5
输出示例2
思路:
1.按照n,m,k构造输入序列v
2.先遍历前k个,统计精华帖子数量,再便利第k+1个,每次加上第i个,减掉第i-k个的值即可
3.返回最大的数量
代码:
#include<iostream>
#include <vector>
using namespace std;
int main(){int n,m,k;cin>>n>>m>>k;vector<vector<int>> p;while(m--){int a,b;cin>>a>>b;vector<int> p1 = {a,b};p.push_back(p1);}vector<int> v(n,0);for(auto it:p){for(int i = it[0];i<it[1];i++){v[i] = 1;}}int res = 0;int sum = 0;for(int i = 0;i<k;i++){res +=v[i];}sum = res;for(int i = k;i<n;i++){sum = sum + v[i] - v[i-k];res = max(res,sum);}cout<<res<<endl;}3.连续子数组最大和
题目描述
小红拿到了一个数组,她希望进行最多一次操作:将一个元素修改为x。小红想知道,最终的连续子数组最大和最大是多少?
输入描述
第一行输入一个正整数t,代表询问次数。对于每次询问,输入两行:
第一行输入两个正整数n和x。代表数组的大小,以及小红可以修改成的元素。第二行输入n个正整数a_i,代表小红拿到的数组
输出描述
输出t行,每行输出一个整数,代表连续子数组的最大和。
输入示例
3
5 10
5 -1 -5 -3 2
2 -3
-5 -2
6 10
4 -2 -11 -1 4 -1
输出示例15
-2
15
思路:(代码随想录)
动态规划:最大子序和 的方法,先求出 [0 - i) 区间的 最大子序和 dp1 和 (i, n)的最大子序和dp2
然后在遍历一遍i, 计算 dp1 + dp2 + vec[i] 的最大值就可以。
正序遍历,求出 [0 - i) 区间的 最大子序,dp[ i - 1] 表示 是 以 下标 i - 1为结尾的最大连续子序列和为dp[i - 1]。
所以 在计算区间 (i, n)即 dp2 的时候,我们要倒叙。因为我们求的是以 包括下标i + 1为起始位置的最大连续子序列和为dp[i + 1]。
这样 dp1 + dp2 + vec[i] 才是一个完整区间。
代码:
#include <iostream>
#include <vector>
#include <climits>
using namespace std;
int main() {int t, n, x;cin >> t;while (t--) {cin >> n >> x;vector<int> vec(n);for (int i = 0; i < n; i++) cin >> vec[i];vector<int> dp1(n);dp1[0] = vec[0];int res = vec[0];// 从前向后统计最大子序和for (int i = 1; i < n; i++) {dp1[i] = max(dp1[i - 1] + vec[i], vec[i]); // 状态转移公式res = max(res, dp1[i]);}res = max(res, vec[n - 1]);// 从后向前统计最大子序和vector<int> dp2(n);dp2[n - 1] = vec[n - 1];for (int i = n - 2; i >= 0; i--) {dp2[i] = max(dp2[i + 1] + vec[i], vec[i]);}for (int i = 0 ; i < n ; i++) {int dp1res = 0;if (i > 0) dp1res = max(dp1[i-1], 0);int dp2res = 0;if (i < n - 1 ) dp2res = max(dp2[i+1], 0);res = max(res, dp1res + dp2res + x);}cout << res << endl;}}
相关文章:
)
刷题记录(20240605)
1.数组构造 题目描述 小红的数组构造小红希望你构造一个数组满足以下条件: 1.数组共有 n个元素,且所有元素两两不相等。 2.所有元素的最大公约数等于 k。 3.所有元素之和尽可能小。请你输出数组元素之和的最小值。 输入描述: 两个正整数 n 和 k。 输出描述ÿ…...

CUDA和OpenGL纹理texture结合
cuda和OpenGL纹理结合,并进行直方图计算 针对于单通道16位图像。结合方式在CUDA_equalizeHistogram_16函数中。 其他的为CUDA核函数。 #define HISTOGRAM_LENGTH 65536 // 2^16 表示16位深度定义直方图长度为65536,对应16位像素值的范围(0-65535)。 __global__ void com…...
市场凌乱,智能算法哪种效果好?
当我们在面对市场波动,个股震荡,无从下手的时候,不懂算法的朋友就只懂做t;懂算法的朋友这会儿就迷茫并不知道选择哪种智能算法交易?今天小编给大家整理一套性价比高的,适合个人投资者搞的算法交易ÿ…...

学会这14大招,30天涨粉两三千没问题!沈阳新媒体运营培训
很多小白在刚转入公司做新媒体时,基本都是从帮助公司运营账号开始的。但不同于个人号,一个企业本身是没有ip属性的,它的风格、调性等,都需要通过你的运营,让它变成一个活灵活现的、赋予独立个性人设的账号。 目前&…...

SQL数据库性能优化
1.查询尽量避免使用select * 1.1 增加磁盘开销:数据库本质上是将记录存储在磁盘上,查询操作就是一种进行磁盘IO的行为,我们查询的字段越多,读取的内容也就越多,对IO磁盘的开销也就会增大,特别是某些字段,如…...

eNSP学习——RIP路由协议基础配置
目录 主要命令 原理概述 实验内容 实验目的 实验拓扑 实验编址 实验步骤 1、基本配置 2、使用RIPv1搭建网络 开启 RIP调试功能 3、使用RIPv2搭建网络 RIPv1和RIPv2的不同 需要eNSP各种配置命令的点击链接自取:华为eNSP各种设备配置命令大全PD…...
)
备考系统架构设计师,看这篇就够了!(包括核心总结、真题、论文、模拟试题索引)
注:以下章节核心总结来自最新版课本:系统架构设计师教程(第2版): https://url35.ctfile.com/f/52515535-1268514286-ca9b3a?p6235 ( 访问密码: 6235, 电子版 pdf 文件大小: 168.9 M ,需要的话可自行下载,…...

stm32编译原理
STM32编译原理主要包括以下几个方面: (1)编译器选择:STM32可以使用多种编译器进行开发,如Keil、IAR、GCC等。不同的编译器有不同的特点和优缺点,需要根据具体需求进行选择。 (2)编…...

如何以JNI方式实现安卓APP控制GPIO?
本文档提供了在 Android 10 设备上通过应用程序(App)控制通用输入输出(GPIO)的详细指南。这涵盖了从创建 gpio驱动到App 配置 以及 SELinux 策略以允许特定访问的所有必要步骤。 1. 驱动实现 添加创建gpio控制驱动bsp\kernel\ke…...

计算机网络学习笔记——运输层(b站)
目录 一、 运输层概述 二、运输层端口号、复用与分用的概念 三、UDP和TCP的对比 四、TCP的流量控制 五、TCP的拥塞控制 六、TCP超时重传时间的选择 七、TCP可靠传输的实现 八、TCP报文段的首部格式 一、 运输层概述 物理层、数据链路层、网络层实现了主机到主机的通信…...
)
HBase数据库面试知识点:第二部分 - 核心技术(持续更新中)
目录 1. 分布式存储与HDFS 2. 面向列的存储 3. 数据版本控制 4. Region与RegionServer 5. 分布式协调服务(ZooKeeper) 1. 分布式存储与HDFS HBase利用Hadoop的HDFS作为其底层存储系统,确保数据的高可靠性和可扩展性。 数据块࿰…...
Spring 使用SSE(Server-Sent Events)学习
什么是SSE SSE 即服务器发送事件(Server-Sent Events),是一种服务器推送技术,允许服务器在客户端建立连接后,主动向客户端推送数据。 SSE 基于 HTTP 协议,使用简单,具有轻量级、实时性和断线重…...
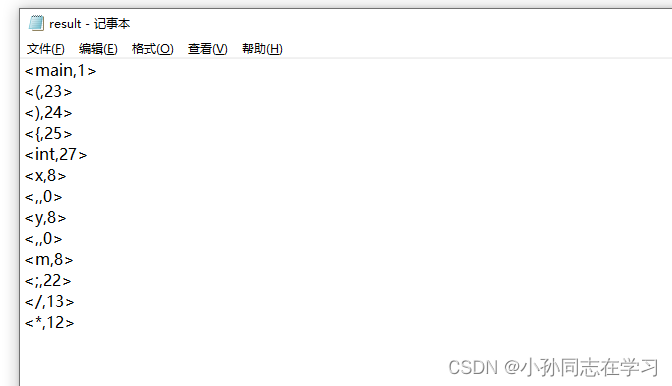
词法分析器的设计与实现--编译原理操作步骤,1、你的算法工作流程图; 2、你的函数流程图;3,具体代码
实验原理: 词法分析是编译程序进行编译时第一个要进行的任务,主要是对源程序进行编译预处理之后,对整个源程序进行分解,分解成一个个单词,这些单词有且只有五类,分别时标识符、关键字(保留字&a…...

linux查看磁盘类型命令
在Linux中,有多种方法可以查看磁盘是固态硬盘(SSD)还是机械硬盘(HDD)。以下是一些常用的方法: 查看/sys/block/目录 /sys/block/目录包含了系统中所有块设备的信息。你可以查看这个目录中的设备属性来判断…...

多线程调用同一个不包含可变状态,并且是线程安全的方法时,可同时执行,不必等待排队
多线程调用同一个不包含可变状态,并且是线程安全的方法时,可同时执行,不必等待排队 前言同时执行方法的条件示例并发执行的优势实验验证总结 前言 如果方法不包含可变状态,并且是线程安全的,那么在高并发环境下&#…...

Java文件操作①——XML文件的读取
系列文章目录 文章目录 系列文章目录前言一、邂逅XML二、应用 DOM 方式解析 XML三、应用 SAX 方式解析 XML四、应用 DOM4J 及 JDOM 方式解析 XMLJDOM 方式解析 XMLDOM4J 方式解析 XML前言 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。…...
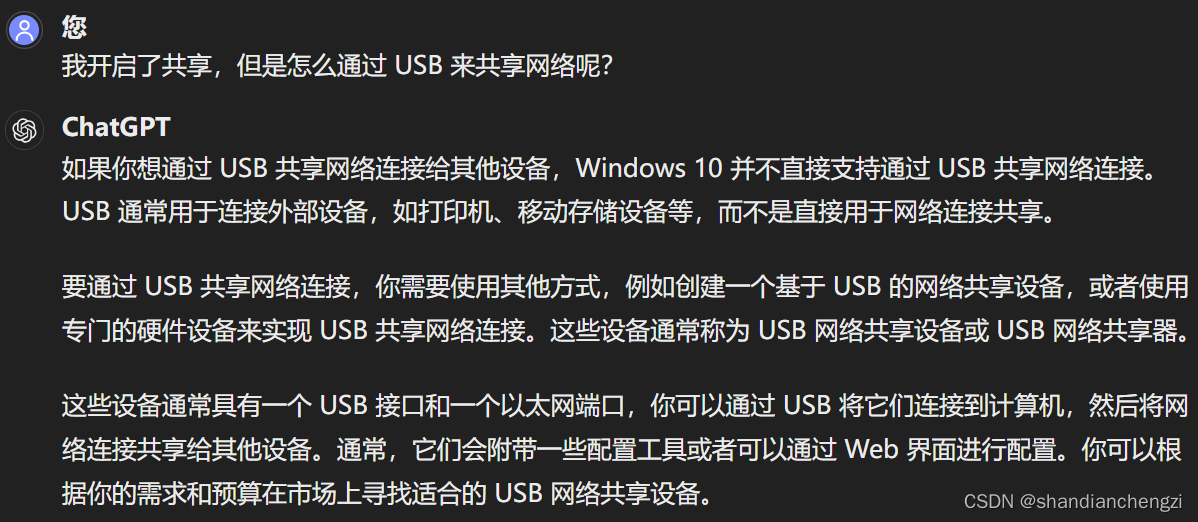
【记录】网络|没有路由器没有网线,分别使用手机或Windows电脑共享网络给ARM64开发板,应急连接
事情是这样的,我的开发板明明已经选择了记住热点 WiFi 密码,但是却没有在开机的时候自动连接,我又没有放显示器在身边,又不想为了这点事去找个显示器来,就非常难受。 我手边有的设备是: 笔记本电脑&#…...
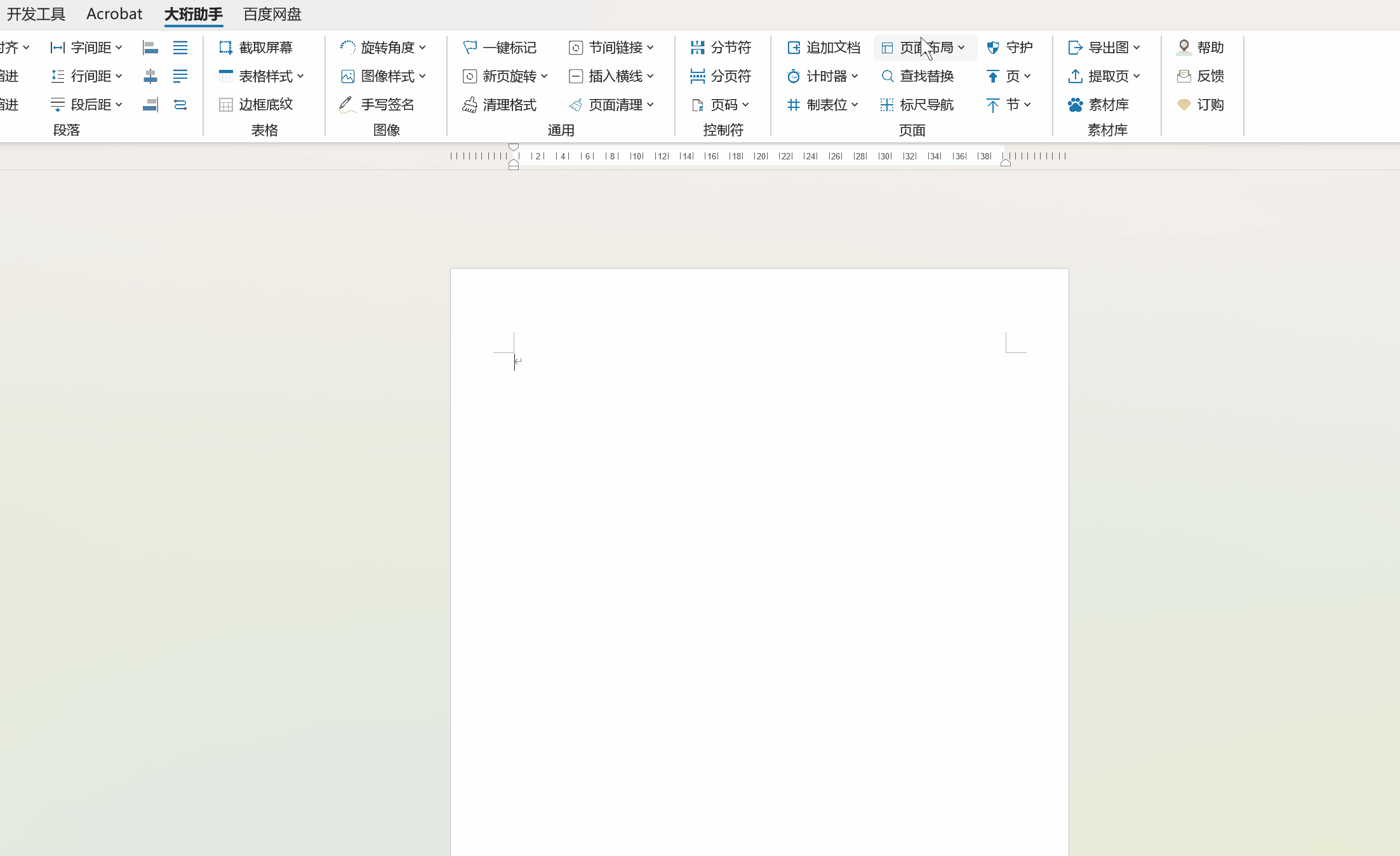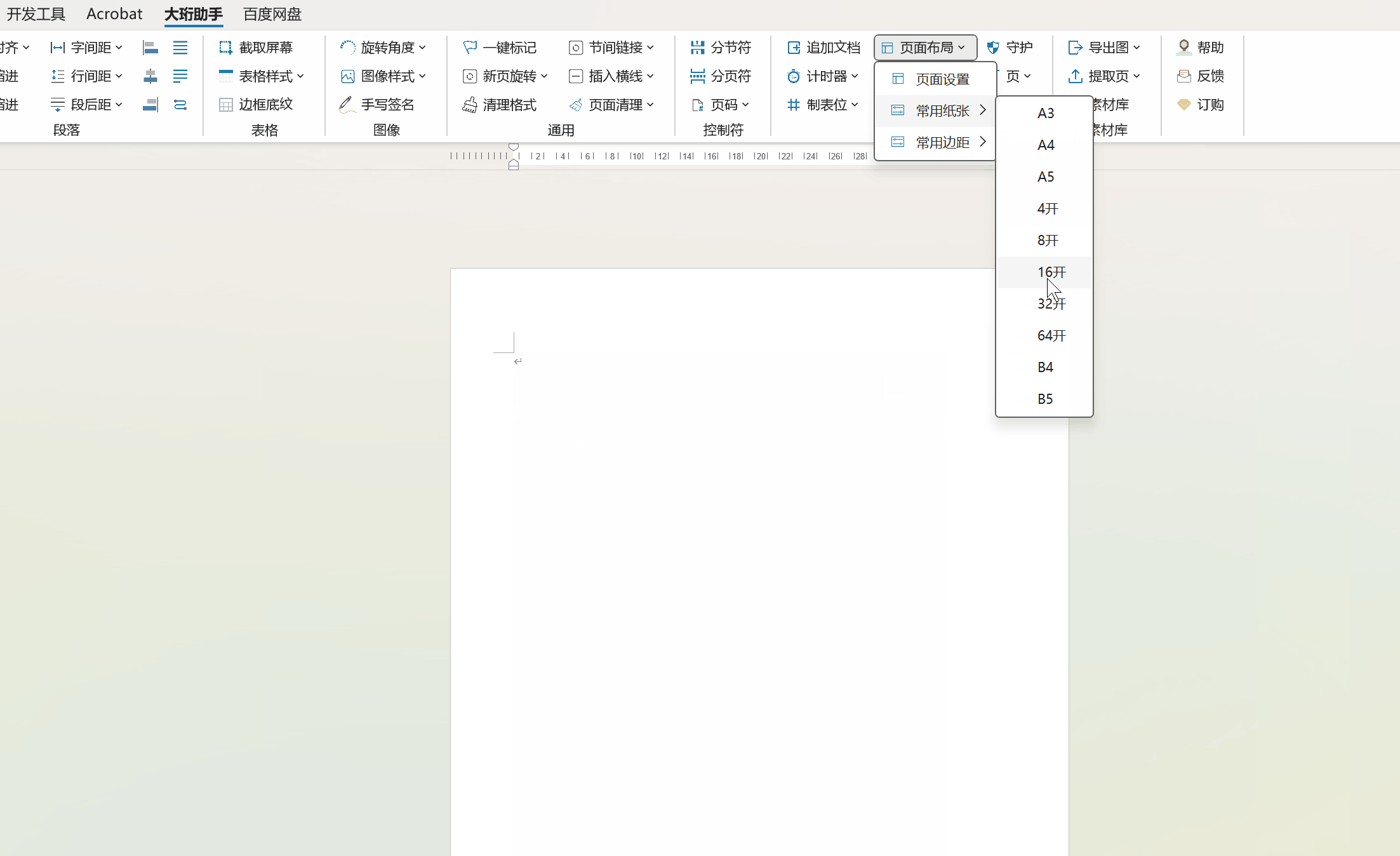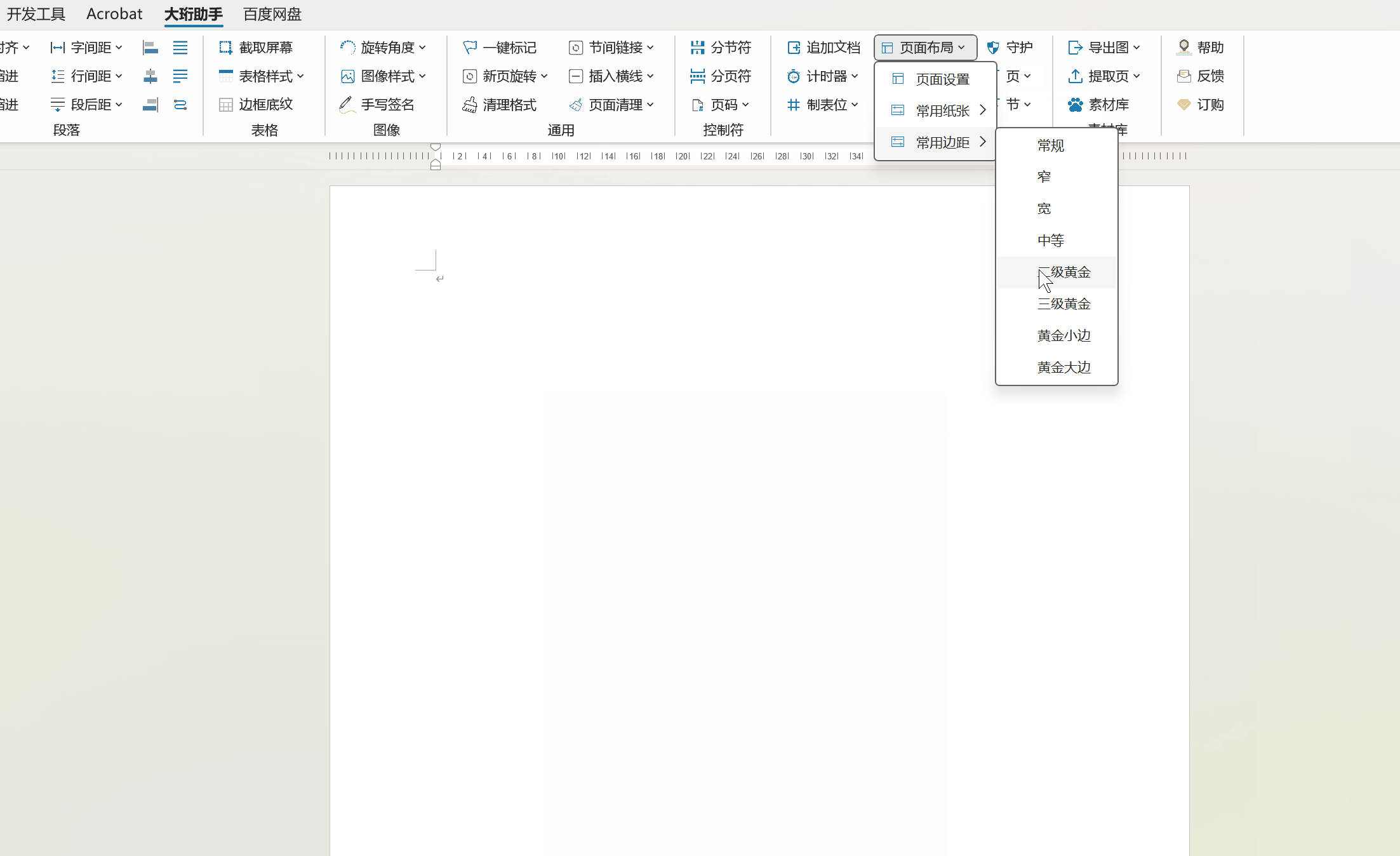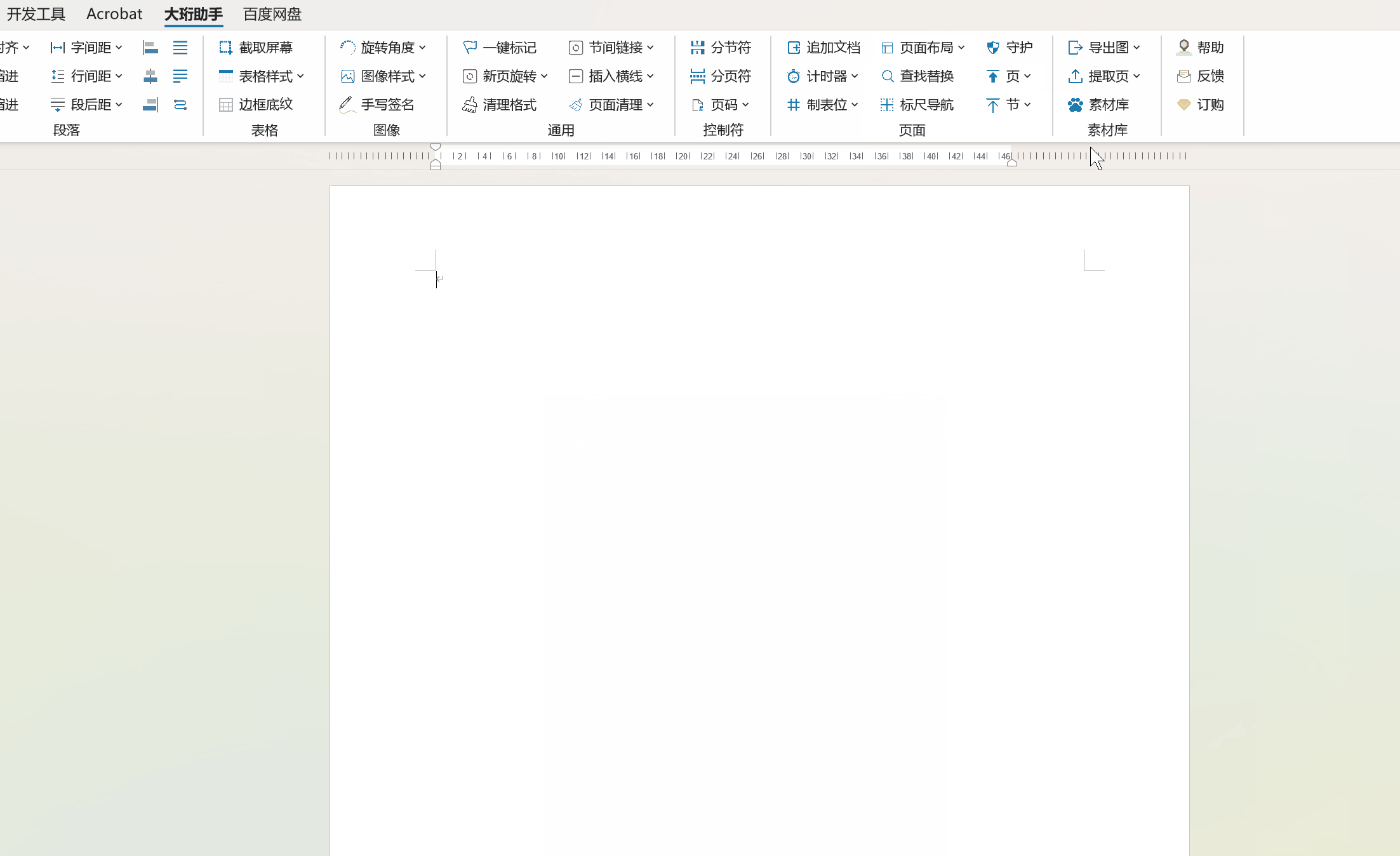
一键设置常用纸张和页面边距-Word插件-大珩助手
Word大珩助手是一款功能丰富的Office Word插件,旨在提高用户在处理文档时的效率。它具有多种实用的功能,能够帮助用户轻松修改、优化和管理Word文件,从而打造出专业而精美的文档。 【新功能】常用纸张和常用边距 1、一键设定符合中国人常用…...
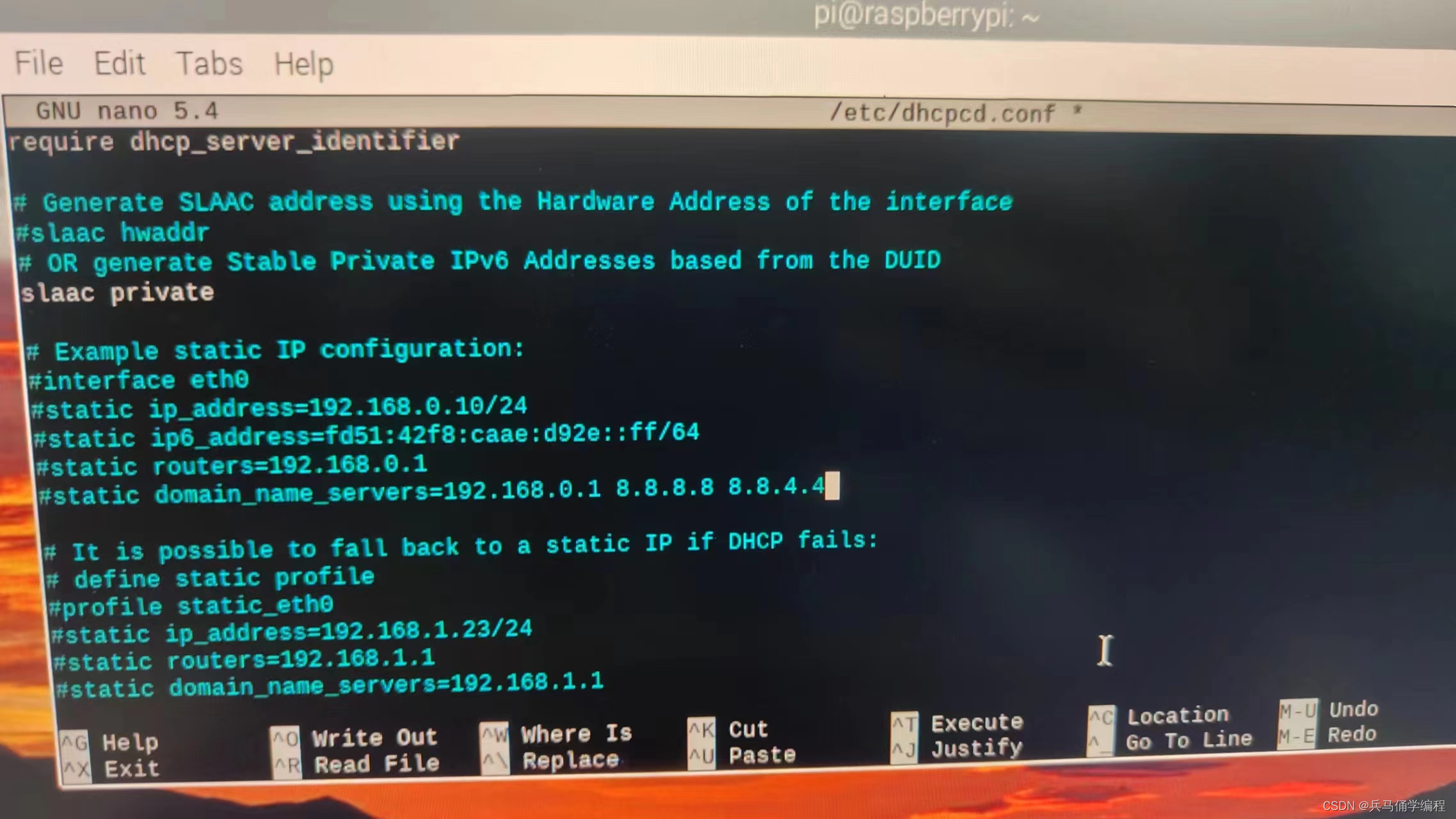
在树莓派3B+中下载opencv(遇到的各种问题及解决)
目录 前言 1、删除原版本下新版本 2、python虚拟环境 3、python版本共存换链接——给版本降低 4、烧录之前版本的文件(在清华源中可以找,不用官网的烧录文件就行; 比如:(balenaEtcher)重新烧录有问题…...

精准检测,安全无忧:安全阀检测实践指南
安全阀作为一种重要的安全装置,在各类工业系统和设备中发挥着举足轻重的作用。 它通过自动控制内部压力,有效防止因压力过高而引发的设备损坏和事故风险,因此,对安全阀进行定期检测,确保其性能完好、工作可靠…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

shell脚本质数判断
shell脚本质数判断 shell输入一个正整数,判断是否为质数(素数)shell求1-100内的质数shell求给定数组输出其中的质数 shell输入一个正整数,判断是否为质数(素数) 思路: 1:1 2:1 2 3:1 2 3 4:1 2 3 4 5:1 2 3 4 5-------> 3:2 4:2 3 5:2 3…...

C# WPF 左右布局实现学习笔记(1)
开发流程视频: https://www.youtube.com/watch?vCkHyDYeImjY&ab_channelC%23DesignPro Git源码: GitHub - CSharpDesignPro/Page-Navigation-using-MVVM: WPF - Page Navigation using MVVM 1. 新建工程 新建WPF应用(.NET Framework) 2.…...
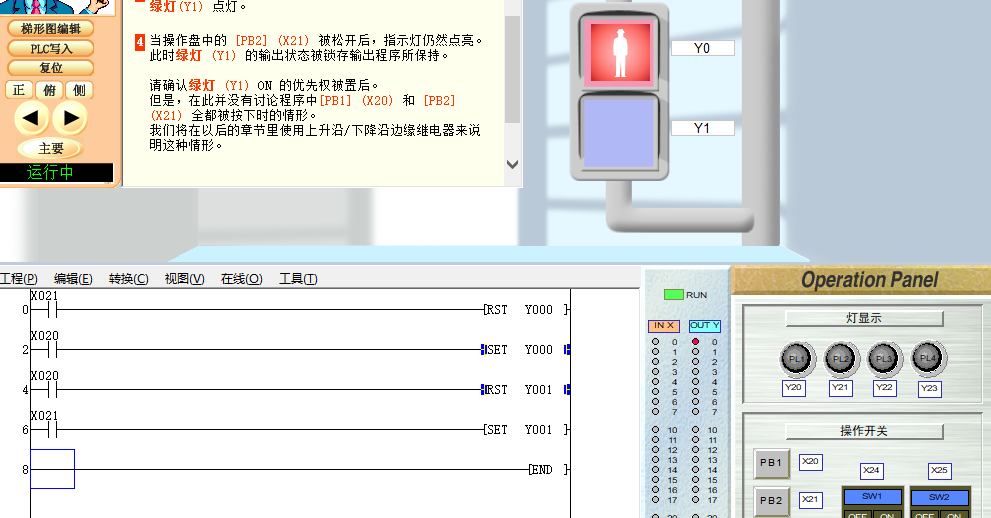
PLC入门【4】基本指令2(SET RST)
04 基本指令2 PLC编程第四课基本指令(2) 1、运用上接课所学的基本指令完成个简单的实例编程。 2、学习SET--置位指令 3、RST--复位指令 打开软件(FX-TRN-BEG-C),从 文件 - 主画面,“B: 让我们学习基本的”- “B-3.控制优先程序”。 点击“梯形图编辑”…...
